基于自动LightGBM的贵州局地大气加权平均温度模型构建

文章编号1000-5269（2024）05-0112-06 DOI：10.15958/j.cnki.gdxbzrb.2024.05.15

摘要：针对贵州地形起伏大、探空站数量少，以及现有大气加权平均温度（Tm）模型不能很好地刻画Tm及其垂向变化的空间差异性和日变化特征等问题，结合贝叶斯超参数优化和LightGBM机器学习方法各自的优势，提出了一种顾及Tm及其垂向变化的空间差异性、年周期、季节周期和日变化特征的自动机器学习建模方法，并以包围威宁探空站的4个ERA5格网点为例，构建了一种无气象参数依赖的贵州局地Tm经验模型（WNTm模型）。实验结果表明：WNTm模型在训练集和验证集上均取得了较高的拟合精度，其不仅可以诊断出Tm的日变特征，还能较好地刻画Tm的垂向变化趋势；以探空站气象资料计算的Tm为参考值，WNTm模型相比于目前较优的GPT3模型取得了更高的预测精度，平均绝对误差和均方根误差分别降低了14.63%和20.14%。该研究方法和思路可为进一步改善Tm的精度提供一种新的途径。

关键词：大气加权平均温度；日变化特征；垂向变化；自动LightGBM 中图分类号：P228.9 文献标志码：A

大气中的大气可降水量（precipitable water vapor， PWV）在大气能量传输、云的形成、天气演变和全球气候变化等方面都扮演着重要作用［1］。基于全球导航卫星系统GNSS的PWV探测技术由于具备高精度、全天候和易于实现高时空分辨率等优点，已发展成为获取PWV的一种有力手段［2］。大气加权平均温度（Tm）是GNSS信号所受对流层天顶湿延迟向PWV转换的关键参量，学者们就如何获取Tm进行了丰富的研究，先后建立了众多Tm模型。总的来说，现有Tm模型可分为两类，即气象因子（surface meteorological factor，SMF）模型和非气象因子（non-meteorological factor，NMF）模型［3］。由于GNSS站点往往缺少同址的气象传感器，导致基于SMF模型难以实现Tm的精确估算。为弥补SMF模型的缺陷，学术界先后建立和发展了大量的区域和全球NMF模型［4-11］，极大地促进了GNSS气象学的发展。然而，受建模所用气象资料时空分辨率低的限制，现有NMF模型大都未能很好地刻画Tm的日变化特征［12］。

受空气中水汽压、大气压及大气温度在空间域和时间域上存在差异性的影响，Tm不仅与地理位置和时间密切相关，而且在高程方向（垂向）存在显著的递减趋势。Tm的垂向变化不仅具有空间差异性，而且在时间域上存在复杂的周期特性［2］，如果忽略Tm的垂向改正，势必将降低PWV的探测精度。为此，针对Tm的垂向改正研究越来越受到重视，如文献［9］在全球范围内基于同一个Tm 垂直递减率，构建了一种全球Tm模型；文献［13］建立了一种中国区域统一的Tm垂直递减率模型，并在此基础上构建了一种顾及垂直递减率的中国区域Tm模型；谢劭峰等［14］针对现有Tm垂直递减率模型数据源单一、难以精确捕获Tm的日变化特征等缺陷，建立了一种高精度的中国区域Tm垂直递减率模型。这些研究较为显著地改善了Tm的精度，可为局地Tm模型的构建提供借鉴。

贵州地势西高东低，高程起伏大，地方性气候差异显著［15］，难以用一个统一的全球模型或区域模型较为精确地表征贵州Tm的时空变化特征。有鉴于此，本文以ERA5高时空分辨率再分析气象资料为数据源，同时顾及Tm及其垂向变化的空间差异性和时域周期特性，基于自动机器学习的方法构建了一种无气象参数依赖的贵州局地Tm经验模型，并采用EAR5和探空站气象资料对模型的精度进行了验证。

1研究区及数据源

1.1研究区

研究区为地处中国西南的贵州省，位于北纬24°37′—29°13′、东经103°36′—109°35′，面积约176 167 km2；区内地貌属高原山地，地势西高东低，最低处高程约为147.8 m，而最高处高达2 900.6 m，平均海拔约1 100 m。受大气环流及多山地形等的影响，区内气候多样性明显，温度和降水的区域差异性显著。

1.2数据源

1.2.1ERA5大气再分析数据集

ERA5是欧洲中期天气预报中心发布的第五代大气再分析产品，可提供逐小时的全球37个等压分层气象资料，其中包括经纬度、位势、比湿、大气温度和大气压等，由此可计算出高时空分辨率的大气加权平均温度。

Tm=∑ni=1（ei/Ti）·Δhi∑ni=1（ei/Ti2）·Δhi（1）

式中：n为大气层数；Ti为相邻大气层的平均温度，K；Δhi为相邻大气层的平均厚度，m；ei为相邻大气层的平均水汽压，hPa。单层水汽压e可采用式（2）进行计算。

e=q0.622+qP （2）

式中：q为比湿，kg/kg；P为大气压，hPa。

由于具备高精度和高时空分辨率的特点，ERA5已被广泛应用于大气加权平均温度的建模和相关气象研究。针对贵州山地气候空间差异性显著的问题，本文以2014—2019年0.25°×0.25°（约31 km×31 km）的逐小时ERA5气象资料作为建模数据源，其中2014—2018年的气象资料用于模型构建，2019年的气象资料用于模型精度验证。为保证Tm的准确性，采用了与文献［16］相同的质量控制措施；同时，鉴于顶层大气压力小于200 hPa时Tm数值差异甚微，故为刻画Tm的垂向变化趋势，实验时基于式（1）分别对各等压层至大气压力为200 hPa大气层的Tm进行了计算，从而每小时1个格网点不同高度处的大气加权平均温度共有22个。

1.2.2无线探空数据

探空站可提供每日0时和12时的实测地表及分层气象数据，主要包括大气压、分层气象数据对应的高程、温度、露点温度，以及测站的经度、纬度和高程信息，可从美国怀俄明州立大学网站下载（http：//weather.uwyo.edu/upperair/sounding.html）。本文选用贵州省威宁（WN）无线探空站2019年的气象数据，在采用式（1）计算出大气加权平均温度的基础上，对Tm模型的精度进行评价。威宁探空站位置图如图1所示。

2建模方法

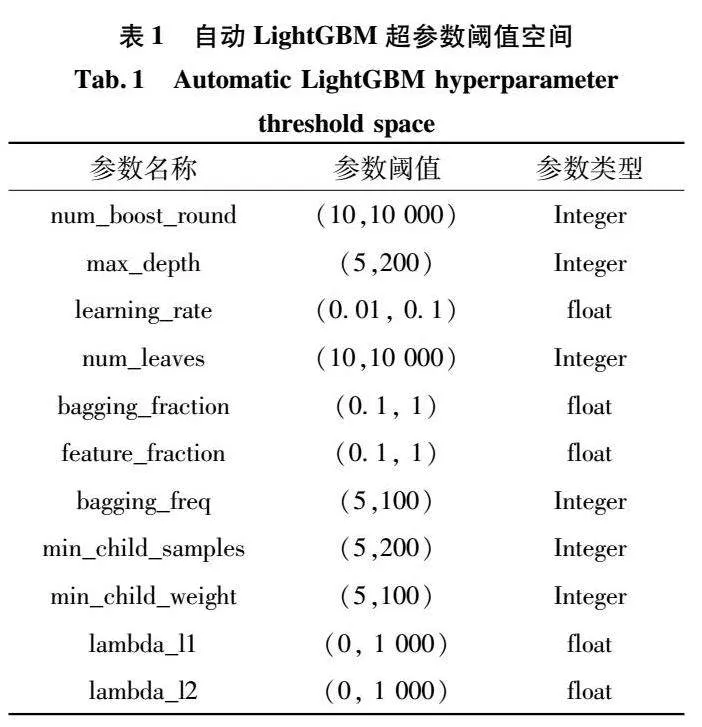
LightGBM是由微软提供的以决策树为学习器的一种梯度提升算法，其不仅能够处理大规模数据，而且具有速度快、精度高和支持并行运算等优点［17］。LightGBM参数众多，人工手动调参费时费力，且不易捕获最优参数组合；网格搜索和随机搜索虽自动化程度高，但网格搜索需以极大的时间成本为代价，随机搜索则易陷于局部最优［18］。贝叶斯超参数优化作为自动机器学习中的重要概念，是一种先进的全局优化自动调参技术，具有较网格搜索和随机搜索更佳的搜索效率和性能［19］。本文采用基于树形结构的贝叶斯优化方法对LightGBM超参数进行全局自动寻优（以下简称“自动Light-GBM”）。

自动LightGBM主要包括超参数阈值空间、目标函数、优化算法、结果4个部分。其中，超参数阈值空间如表1所示；目标函数使用了5折交叉验证，并采用均方根误差作为评价指标；优化算法采用algo=tpe.suggest；结果即为目标函数的评估结果，包含超参数和验证损失。

3贵州局地Tm模型精度评价

3.1精度评价指标

以ERA5和探空站Tm为参考值，采用平均绝对误差（MAE，EMA）、均方根误差（RMSE，ERMS）和决定系数（R2）3个指标对贵州局地大气加权平均Tm模型的精度进行评价。各指标计算公式如下：

EMA=1N∑Ni=1（YOi-YTi）（3）

ERMS=1N∑Ni=1（YOi-YTi）2（4）

R2=1-∑Ni=1（YTi-YOi）2∑Ni=1（YTi-Y）2（5）

式中：N为Tm的个数；YOi为Tm的模型拟合值或预测值；YTi为Tm的参考值（或真值）；Y为Tm模型拟合值或预测值的均值。

3.2贵州局地大气加权平均温度模型的建立及精度评价

3.2.1模型的建立

Tm及其垂向变化除表现出显著的空间差异性外，还具有年周期、季节周期和日周期特性［11-12］。因此，为提升Tm模型的精度，本文顾及Tm及其垂向变化的空间差异性、年周期、季节周期和日变化特征，以地理位置（经度lon，纬度lat）、年（year）、年积日（day of year，doy）、日积时（hour of day，hod）以及高程（height）为自变量，基于自动LightGBM构建无气象参数依赖的贵州局地Tm经验模型。Tm模型可简单表示为

Tm=F[lon，lat，height，year，doy，hod]1

[lon，lat，height，year，doy，hod]2

…

[lon，lat，height，year，doy，hod]i

…

[lon，lat，height，year，doy，hod]n（6）

式中：自变量[lon，lat，height，year，doy，hod]i包含了4个格网点的地理坐标、各格网点第i年每天逐小时分层大气加权平均温度对应的高程（height）和时间（year、doy、hod）。

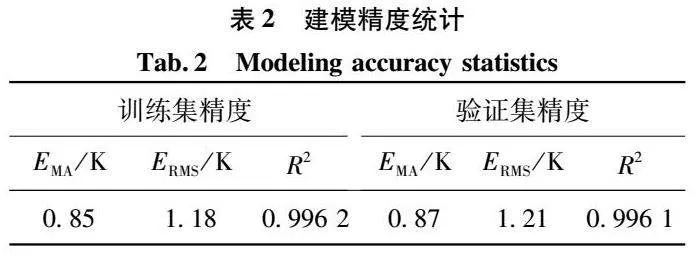
鉴于区域Tm模型较全球Tm模型具有更高的精度［20］，限于篇幅，并为方便采用探空站Tm对贵州局地Tm模型的精度进行评价，本文仅以包围威宁探空站的4个ERA5格网点为例，构建威宁大气加权平均温度模型（WNTm）。同时，为提升模型泛化能力，建模时按6∶4划分训练集和验证集，建模精度统计如表2所示。

由表2可知，WNTm在训练集和验证集上的EMA、ERMS和R2分别为0.85 K、1.18 K、0.996 2和0.87 K、1.21 K、0.996 1，说明WNTm在训练集和验证集上均获得了较高的拟合精度。为进一步探究各变量对贵州局地Tm的影响，绘制自变量特征重要性，如图2所示。

由图2可以看出：自变量对Tm的影响程度由高到低排序依次为doy、height、hod、year、lat和lon。其中，doy和height对Tm的影响占绝对主导，说明Tm具有明显的季节周期，且Tm在高程方向上的变化较为显著；影响程度较小的是hod和year，说明Tm除具有日周期特性外，还表现出一定的年趋势，但年趋势没有季节周期和日周期明显。此外，lat和lon对Tm的影响最小，lat对Tm的影响较lon稍大，这可能是由于建模所用4个格网点距离较近， Tm数值本身差异不是十分显著所致。

3.2.2模型精度评价

以包围威宁探空站4个角点（左上、右上、左下、右下）2019-6-1T12：0：0的EAR5各层大气加权平均温度为参考值，对WNTm模型刻画Tm垂向变化特征的能力进行评价，结果如图3所示。

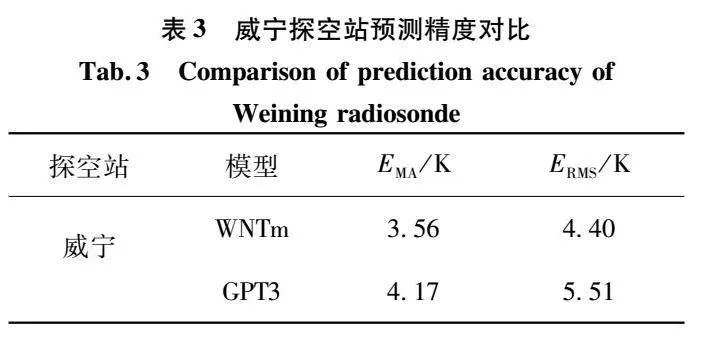
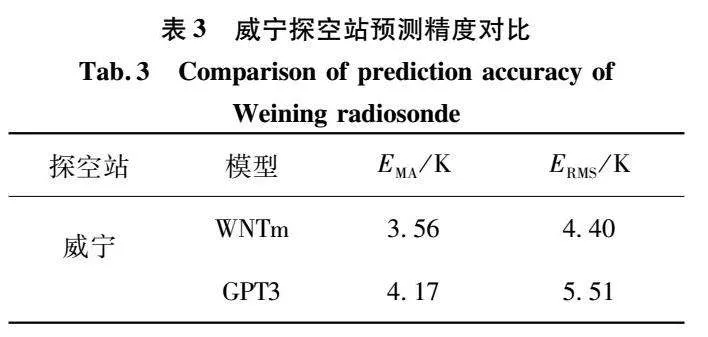
由图3可看出，WNTm模型预测值在高程方向与参考值间具有十分相似的变化趋势，决定系数均大于0.99，说明所建模型能够很好地描述Tm的垂向变化特征。此外，预测值与参考值间的相关性随纬度的升高有所降低，而同一纬度方向的变化却很小，说明Tm垂向变化受纬度的影响更大。由于探空站气象资料为实测数据，具有较高的精度，本文以2019年威宁探空站的Tm为参考值，对模型的预测性能作进一步评价，并将其与GPT3模型的预测值进行比较，结果如表3和图4所示。

由表3可知：以探空站Tm为参考值，WNTm模型预测值的EMA和ERMS分别为3.56 K和4.40 K；GPT3模型预测值的EMA和ERMS分别为4.17 K和5.51 K，WNTm模型较GPT3模型的预测精度分别提升了14.63%和20.15%。由图4可进一步看出，探空站Tm、WNTm模型预测值和GPT3模型预测值三者的变化趋势一致，但GPT3模型的预测值整体偏大，原因可能是威宁探空站海拔较高（高程为2 236 m），GPT3模型不能很好地刻画Tm的垂向变化趋势，而WNTm模型不仅可较好地表征Tm的垂向变化趋势，还可较好地体现Tm的日变化特征。

4结语

结合贝叶斯超参数优化和LightGBM机器学习方法各自的优势，本文提出了一种顾及Tm及其垂向变化空间差异性和时域周期特性的大气加权平均温度建模方法。同时，为方便对模型精度进行评价，以威宁探空站为例，基于4个ERA5格网点气象数据构建了一种无气象参数依赖的WNTm大气加权平均温度经验模型。在此基础上，分别以ERA5和探空站Tm为参考值，对模型的建模精度、模型垂向变化特征的表达能力和预测性能进行了评价。结果表明：WNTm模型取得了较高的建模精度，在训练集和验证集上的EMA、ERMS和R2分别为0.85 K、1.18 K、0.996 2和0.87 K、1.21 K、0.996 1；WNTm模型不仅可以探测出Tm的年、季节和日变化特征，还能较好地刻画Tm的垂向变化趋势，Tm垂向预测值与对应参考值间的决定系数均接近于1，统计学上表现为极强相关；以探空站Tm为参考值，所建模型相较于GPT3模型取得了更高的预测精度，EMA和ERMS分别降低了14.63%和20.15%。以上结论证明了本文所提建模方法和思路的有效性和可靠性，可为进一步改善Tm精度的相关研究提供参考。

参考文献：

[1]WANG J H， ZHANG L Y， DAI A， et al. A near-global， 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements［J］. Journal of Geophysical Research， 2007， 112（D11）： D11107.1- D11107.17.

［2］ HUANG L K， LIU L L， CHEN H， et al. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China［J］. GPS Solutions， 2019， 23： 51.1-51.16.

［3］ LONG F Y， HU W S， DONG Y F， et al. Neural network-based models for estimating weighted mean temperature in China and adjacent areas［J］. Atmosphere， 2021，12： 169.1-169.27.

［4］ 曲双宝. 一种新的青藏高原地区加权平均温度模型［J］. 无线电工程， 2023， 53（4）： 844-852.

［5］ ZHAO Q Z， LIU K， ZHANG T X， et al. A global conversion factor model for mapping Zenith total delay onto precipitable water［J］. Remote Sensing， 2022， 14： 1086.1-1086.17.

［6］ 石灵璠， 王萍， 黄良珂. 青藏高原地区大气加权平均温度模型的构建［J］. 测绘通报， 2021（4）： 52-59.

［7］ LANDSKRON D， BOHM J. VMF3/GPT3： refined discrete and empirical troposphere mapping functions［J］. Journal of Geodesy， 2018， 92（4）： 349-360.

［8］ BOHM J， MOLLER G， SCHINDELEGGER M， et al. Development of an improved empirical model for slant delays in the troposphere （GPT2w）［J］. GPS Solutions， 2015， 19（3）： 433-441.

［9］ YAO Y B， XU C Q， ZHANG B， et al. GTm-III： a new global empirical model for mapping zenith wet delays onto precipitable water vapour［J］. Geophysical Journal International， 2014， 197（1）： 202-212.

［10］YAO Y B， ZHANG B， YUE S Q， et al. Global empirical model for mapping zenith wet delays onto precipitable water［J］. Journal of Geodesy， 2013， 87： 439-448.

［11］YAO Y B， ZHU S， YUE S Q. A globally applicable， season-specific model for estimating the weighted mean temperature of the atmosphere［J］. Journal of Geodesy， 2012， 86（12）： 1125-1135.

［12］SUN Z Y， ZHANG B， YAO Y B. An ERA5-based model for estimating tropospheric delay and weighted mean temperature over China with improved spatiotemporal resolutions［J］. Earth and Space Science， 2019， 6（10）： 1926-1941.

［13］黄良珂， 彭华， 刘立龙， 等. 顾及垂直递减率函数的中国区域大气加权平均温度模型［J］. 测绘学报， 2020， 49（4）： 432-442.

［14］谢劭峰， 王义杰， 黄良珂， 等. 中国区域大气加权平均温度垂直递减率格网模型［J］. 测绘学报， 2023， 52（2）： 206-217.

［15］焦权. 典型喀斯特微流域土壤资源赋存及小气候特征［D］. 贵州： 贵州大学， 2018.

［16］HE C Y， WU S Q， WANG X， et al. A new voxel-based model for the determination of atmospheric weighted mean temperature in GPS atmospheric sounding［J］. Atmospheric Measurement Techniques， 2017， 10（6）： 2045-2060.

［17］KE G L， MENG Q， FINLEY T， et al. LightGBM： a highly efficient gradient boosting decision tree［C］// Proceedings of the 31st International Conference on Neural Information Processing Systems， NY： Curran Associates Inc.， 2017： 3149-3157.

［18］JLASSI S， JDEY I， LTIFI H. Bayesian hyperparameter optimization of deep neural network algorithms based on ant colony optimization［C］// ICDAR 2021， Cham： Springer Nature Switzerland AG， 2021： 585-594.

［19］SNOEK J， LAROCHELLE H， ADAMS R P. Practical Bayesian optimization of machine learning algorithms［C］// Proceedings of the 25th International Conference on Neural Information Processing Systems， NY： Curran Associates Inc.， 2012： 2951-2959.

［20］HUANG L K， JIANG W P， LIU L L， et al. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor［J］. Journal of Geodesy， 2019， 93（2）： 159-176.

（责任编辑：周晓南）

Abstract：

To address the problems of large topographic fluctuation， small number of radiosonde in Guizhou， and the fact that the existing weighted mean temperature （Tm） model can not describe the spatial difference and diurnal variation of Tm and its vertical variation. This paper combined the advantages of Bayes hyperparameter optimization and LightGBM machine learning method， thus proposed an automatic machine learning modeling method， which took into account the spatial difference， annual cycle， seasonal cycle and diurnal variation of Tm and its vertical variation. A local empirical model of Tm （WNTm model） in Guizhou province without meteorological parameter dependence is constructed by taking 4 ERA5 grid points surrounding Weining Sounding Station as an example. The experimental results show that the WNTm model achieves high fitting accuracy on both training set and verification set. It can not only diagnose the diurnal characteristics of Tm， but also describe the vertical variation trend of Tm well. Compared with the current better GPT3 model， WNTm model can achieve higher prediction accuracy， and the mean absolute error and root-mean-root error are reduced by 14.63% and 20.14% respectively. The research methods and ideas in this paper can provide a new way to further improve the accuracy of Tm.

Key words：

atmospheric weighted mean temperature; daily variation characteristics; vertical variation; automatic LightGBM

收稿日期：2024-05-17

基金项目：贵州大学“SRT计划”资助项目（贵大SRT字[2022]332号）

作者简介：方省（2001—），女，贵州大学矿业学院2020级测绘工程专业在读本科生，E-mail：14785221693@163.com.

*通讯作者：张显云，E-mail：mec.xyzhang@gzu.edu.cn.