磁悬浮列车的悬浮架系统自由振动特性研究

文章编号1000-5269（2024）05-0084-11 DOI：10.15958/j.cnki.gdxbzrb.2024.05.12

摘要：高温超导钉扎磁悬浮列车的悬浮架系统自由振动特性会影响乘客的安全性和舒适性，对其研究十分重要。通过实验装置采集高温超导块组合和永磁轨道间的悬浮数据，得到悬浮力的经验公式，基于经验公式建立悬浮架系统垂向振动的动力学模型；利用多尺度法推导并验证悬浮架系统的悬浮间隙响应的近似解；基于悬浮间隙近似解得到了最大超调量和最大加速度的表达式，研究单位质量阻尼和单位质量刚度对最大超调量和最大加速度的影响，基于磁悬浮标准中的衰减性和舒适性两个动力学指标提出了一种确定系统参数可行域的方法。研究表明单位质量阻尼应小于19.6s-1，单位质量刚度应小于139s-2，且系统参数的可行域近似为扇形。本文的研究结果为悬浮架系统的参数设计提供了理论支撑。

关键词：悬浮架系统；悬浮力；多尺度法；近似解；系统参数可行域 中图分类号：U237 文献标志码：A

磁悬浮列车与传统的轮轨式列车相比，具有爬坡能力强、振动小，平稳舒适、污染小［1］等显著的优点，符合当今绿色发展的理念。除德国的电磁悬浮列车和日本的电动磁悬浮列车［2］以外，我国具有完全自主知识产权的高温超导钉扎磁悬浮列车（简称“高温超导磁悬浮列车”）引起了国内外的广泛关注。高温超导磁悬浮列车利用了高温超导体的磁通钉扎效应，即当利用液氮冷却高温超导体时，永磁轨道的部分磁场被高温超导体的钉扎点捕获固定，这时捕获磁场和永磁轨道磁场相互作用产生宏观的悬浮力，使高温超导体稳定悬浮在永磁轨道的上方［3］。然而高温超导钉扎磁悬浮列车在高速运行时因轨道变形、轨道不平顺或空气阻力等因素引起悬浮架系统发生振动，进而改变悬浮架本体和永磁轨道之间的悬浮间隙。由于悬浮间隙能否快速回复到平衡位置会影响乘客的安全性和舒适性，因此研究高温超导钉扎磁悬浮列车的悬浮架系统参数对列车振动特性的影响十分重要。

近年来，国内外众多学者对高温超导钉扎磁悬浮的静态和动态特性进行了研究。上世纪80年代，HELLMAN［4-5］等研究并发现了高温超导体块材和永磁铁之间存在着磁悬浮现象。COOMBS［6-7］等对高温超导体在轴对称磁场中的行为进行研究，提出了引发系统共振的临界模型。TESHIMA［8-9］等搭建了实验台，研究得到了磁悬浮固有频率的变化规律。HIKIHARA［10-11］等研究得到了高温超导悬浮系统准周期振动下的分形和混沌等行为。王晓融［12］研究了高温超导体在永磁轨道上所受的导向力，得到了YBCO块材的参数对悬浮系统导向能力的影响。MOON等［13］通过研究永磁体与超导陶瓷材料之间的磁力，发现了磁力随悬浮间隙的变化时具有明显滞回行为。勾艳凤［14］研究了不同场冷高度下高温超导磁悬浮样车的自由振动，得到了不同条件下样车垂向与横向固有频率的变化规律。肖玲等［15］研究了高温超导体和磁体的尺寸对悬浮力的影响，得到了最大悬浮力随永磁体直径的增大先增大后减小，当永磁体直径和超导块直径相同时达到最大。DENG等［16］通过分析高温超导磁悬浮列车的自由振动特性，研究得到了刚度随场冷高度的增大而减小，而阻尼系数与场冷高度的关系比较复杂的结论。LIU等［17］研究了捕获磁场对悬浮力的影响，结果表明高温超导体捕获磁场越大，悬浮力也越大。张兴义等［18］基于高温超导块材时效和记忆特性的试验，发现了在零场冷悬浮力的随机现象以及场冷条件下悬浮力呈现逐渐增大的现象。胡博等［19］针对永磁圆盘轨道沉降问题搭建了高温超导磁悬浮动态测控系统，对测控系统的硬件架构、软件架构和控制算法进行了研究。李刚等［20］研究了YBCO堆叠磁体磁悬浮系统中的传递效率与基振加速度幅值和基振频率的关系，研究表明自由振动频率在9Hz左右。杨文姣等［21］基于三维电磁-热-力多物理场强耦合模型提出了研究高温超导磁悬浮振动特性的模拟方法。任晓晨等［22］研究了高温超导磁悬浮装置空间磁场交变及不均匀性扰动会引发超导块材内部损耗的问题。陈楠等［23］为提高高温超导磁悬浮实验车的载重，提出了一种高温超导-永磁混合悬浮车系统概念及理论设计方法。ZHANG等［24］对高温超导磁悬浮列车的准静力学进行研究，并利用多体动力学软件UM仿真分析了列车在直线运行的性能。张明亮等［25］研究了面向高温超导磁悬浮列车的悬浮特性，提出了一种等效处理高温超导体的方法，并通过实验进行了验证。

综上所述，尽管目前不同专家学者对高温超导磁悬浮列车的静态和动力学性能及振动特性进行了研究，但在自由振动下的演化行为涉及较少。本文建立悬浮架系统的垂向动力学模型，对悬浮力和悬浮间隙的磁轨关系进行拟合，利用多尺度法求解非线性动力学方程，分析悬浮架系统在自由振动下的动态响应特性，提出了一种判断系统参数可行域的方法，基于磁悬浮标准中的衰减性和舒适性动力学指标得到了悬浮架系统参数的许用范围。

1悬浮力经验公式的获得

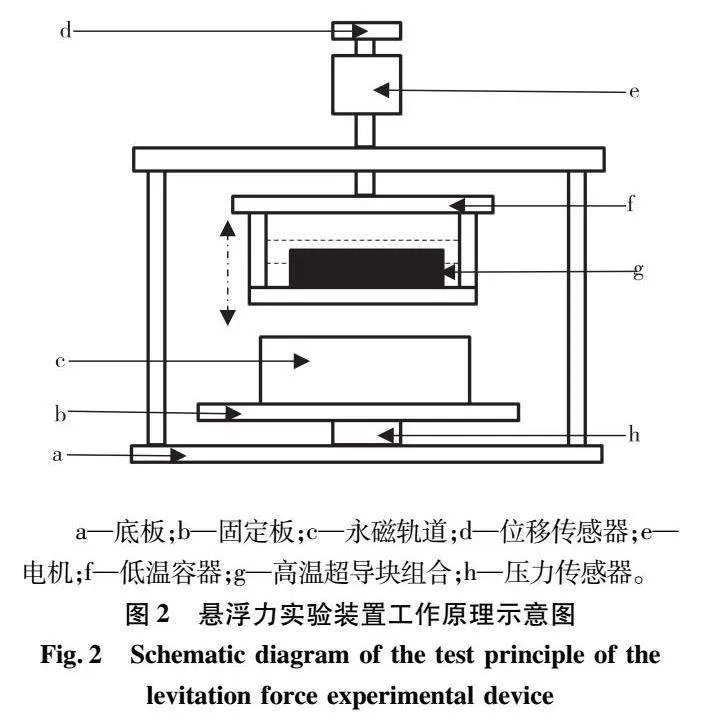
本文采用的悬浮力实验装置，如图1所示，实验装置工作原理示意图如图2所示。

实验装置主要由位移传感器、压力传感器、电机、低温容器、高温超导块组合和永磁轨道组成。其中，位移传感器安装在电机上，通过电机的转速和丝杆螺母的螺距，可以得到上下移动的距离；低温容器固定连接在电机转轴的端部，可以通过电机带动上下运动（见虚线双向箭头）；高温超导块组合固定在低温容器中；压力传感器安装在永磁轨道固定板和机座底板之间，通过永磁轨道受到的压力反映悬浮力的大小。实验测试的基本步骤：利用电机旋转丝杆螺母机构产生的直线运动移动低温容器，使高温超导块组合接近永磁轨道，保持两者之间的距离不变，即设定场冷高度hch；然后将液氮倒入到低温容器中，使高温超导块组合在永磁轨道的磁场下冷却进入超导态（即场冷）；高温超导块组合在电机的带动下向上移动，位移传感器测量获得向上移动的悬浮间隙，压力传感器测量获得悬浮力。

利用上述实验装置，测量在场冷高度25mm时单个高温超导块组合和永磁轨道的悬浮力。将悬浮力看作变刚度的弹簧，以二次多项式进行拟合得到经验公式，得到实验数据和经验公式的对比关系，如图3所示。

由图3可知，悬浮力随着悬浮距离的增大而增大，且实验数据和拟合经验公式对比较好，由此验证二次多项式拟合的经验公式的有效性。

本文中悬浮架系统的悬浮力由高温超导块组合和永磁轨道提供。假定需要承载100kg，则悬浮架本体左右两侧各安装200组高温超导块组合与永磁轨道配合，则将上述测量的单个高温超导块组合与永磁轨道的悬浮力乘以400倍即可得到悬浮架系统的悬浮力。在悬浮架系统中垂直方向上除了受向上的悬浮力影响还受到向下重力的影响，将悬浮架系统的悬浮力和重力看作合力，得到

Fsumz=FZ－mg=k2zz2+k1zz+c0－mg（1）

式中：Fsum为悬浮力和重力的合力；k1z为线性刚度系数；z为高温超导块组合和永磁轨道的悬浮间隙；k2z为非线性刚度系数；c0为常数项；m为悬浮架本体的质量；g为重力加速度。

由于合力的平衡位置对应的悬浮间隙zeq不等于0，为了后续分析方便，需根据坐标平移原理将平衡点移到原点O处。

令z=u+zeq，将其代入式（1）中整理变形可得

Fsum=k1u+k2u2（2）

式中：k1为平移后系统的线性刚度系数；k2为平移后系统的非线性刚度系数；u为距离平衡位置的偏移间距。

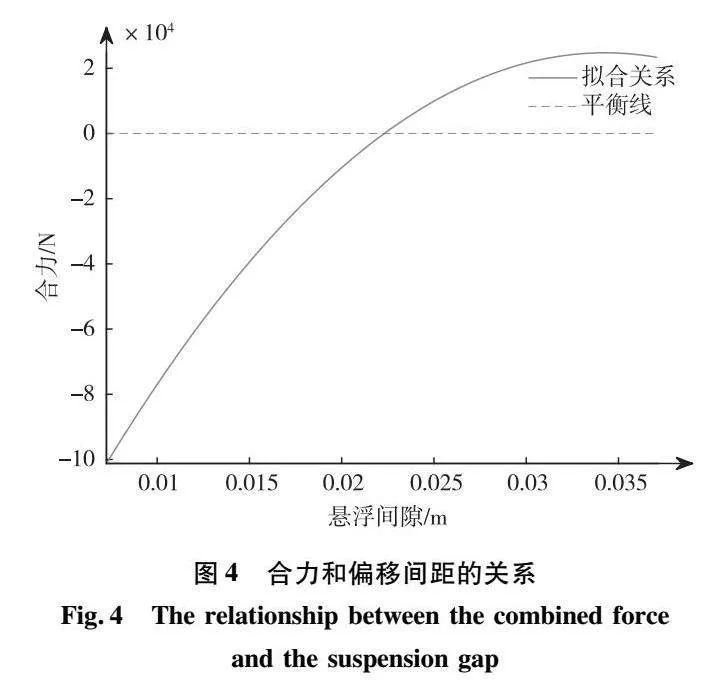
由式（2）可以得到悬浮力和重力的合力Fsum与偏移间距的拟合关系，如图4所示。

由图4可知，当偏移间距小于0时，合力小于0，表现为悬浮架本体上的高温超导块组合阻止靠近永磁轨道；当偏移间距大于0时，即合力大于0，表现为悬浮架本体上的高温超导块组合阻止远离永磁轨道。

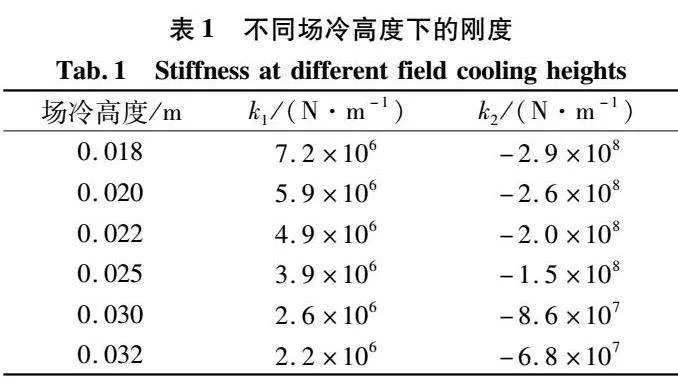
将不同场冷高度下合力和偏移间距进行拟合，得到线性刚度k1和非线性刚度k2，见表1。

由表1可知，线性刚度k1大于0，非线性刚度k2小于0；线性刚度k1随着场冷高度的增大而减小，而非线性刚度k2的大小随着场冷高度的增大而减小。

2高温超导钉扎磁悬浮列车悬浮架系统的动力学建模

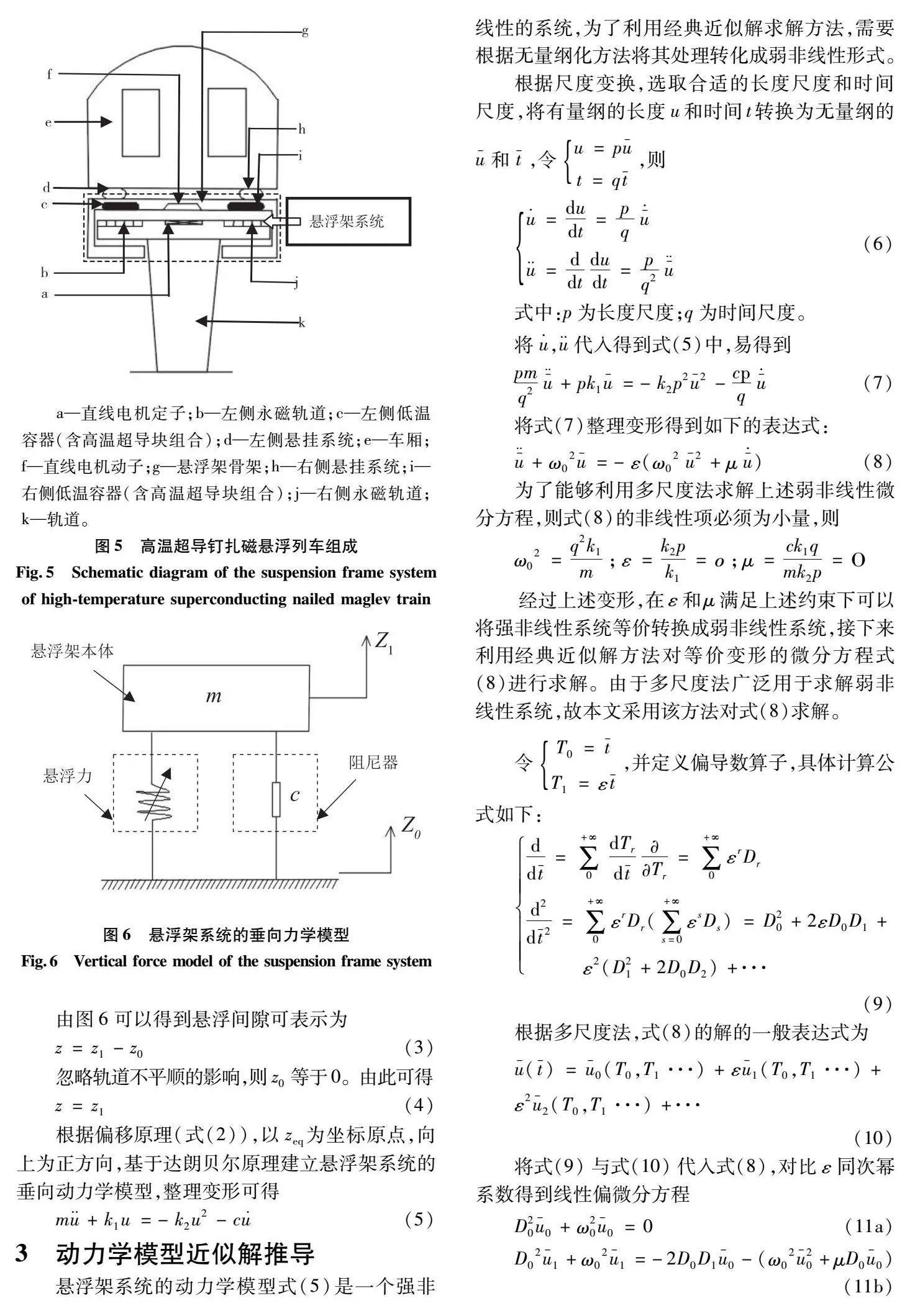
高温超导磁悬浮列车主要组成部分，如图5所示。

由图6可以得到悬浮间隙可表示为

z=z1－z0（3）

忽略轨道不平顺的影响，则z0等于0。由此可得

z=z1（4）

根据偏移原理（式（2）），以zeq为坐标原点，向上为正方向，基于达朗贝尔原理建立悬浮架系统的垂向动力学模型，整理变形可得

m+k1u=－k2u2－c（5）

3动力学模型近似解推导

悬浮架系统的动力学模型式（5）是一个强非线性的系统，为了利用经典近似解求解方法，需要根据无量纲化方法将其处理转化成弱非线性形式。

根据尺度变换，选取合适的长度尺度和时间尺度，将有量纲的长度u和时间t转换为无量纲的u-和t-，令u=pu-t=qt-，则

u·=dudt=pqu-·=ddtdudt=pq2u-¨（6）

式中：p为长度尺度；q为时间尺度。

将u·，代入得到式（5）中，易得到

pmq2u-¨+pk1u-=－k2p2u-2－cpqu-·（7）

将式（7）整理变形得到如下的表达式：

u-¨+ω02u-=-ε（ω02u-2+μu-·）（8）

为了能够利用多尺度法求解上述弱非线性微分方程，则式（8）的非线性项必须为小量，则

ω02=q2k1m;ε=k2pk1=ο;μ=ck1qmk2p=Ο

经过上述变形，在ε和μ满足上述约束下可以将强非线性系统等价转换成弱非线性系统，接下来利用经典近似解方法对等价变形的微分方程式（8）进行求解。由于多尺度法广泛用于求解弱非线性系统，故本文采用该方法对式（8）求解。

令T0=t-T1=εt-，并定义偏导数算子，具体计算公式如下：

ddt-=∑+∞0dTrdt-Tr=∑+∞0εrDrd2dt-2=∑+∞0εrDr（∑+∞s=0εsDs）=D20+2εD0D1+ε2（D21+2D0D2）+···（9）

根据多尺度法，式（8）的解的一般表达式为

u-（t-）=u-0（T0，T1···）+εu-1（T0，T1···）+

ε2u-2（T0，T1···）+···（10）

将式（9）与式（10）代入式（8），对比ε同次幂系数得到线性偏微分方程

D20u-0+ω20u-0=0（11a）

D02u-1+ω02u-1=－2D0D1u-0－（ω02u-20+μD0u-0）（11b）

根据线性方程求解，易得式（11a）解的形式为

u0=eiT0w0A（T1）+e－iT0w0B（T1）（12）

其中，B（T1）是A（T1）的共轭部分，将式（12）代入式（11b）中，为消除永年项，整理变形得到

A′（T1）=-μA（T1）2B′（T1）=-μB（T1）2（13）

为方便求解，将其写成指数的形式如下：

A（T1）=a（T1）eiw0φ（T1）2B（T1）=a（T1）e－iw0φ（T1）2（14）

将式（14）求导代入式（13），然后分离虚实部，整理求得

a′（T1）=－12μa（T1）φ′（T1）=0（15）

取通用的初始条件

u-0（0）=a0u-·0（0）=0（16）

根据式（12）的通用形式，求解整理可得

u-0（t-）=－a04ω02+ε2μ22ω0×e－12εμt-cos（ω0t-+arccos－2ω04ω02+ε2μ2）（17）

将长度尺度p和时间尺度q代入式（17），并由坐标平移逆变换z=u+zeq，可得悬浮架系统的悬浮间隙的一次近似解表达式如下：

z（t）=－εk2a04mk12+k1c22m×e－ct2mcos（k1mt+arccos－2mk14mk1+c2）+zeq（18）

4悬浮架系统的动态响应特性分析和讨论

4.1近似解的验证

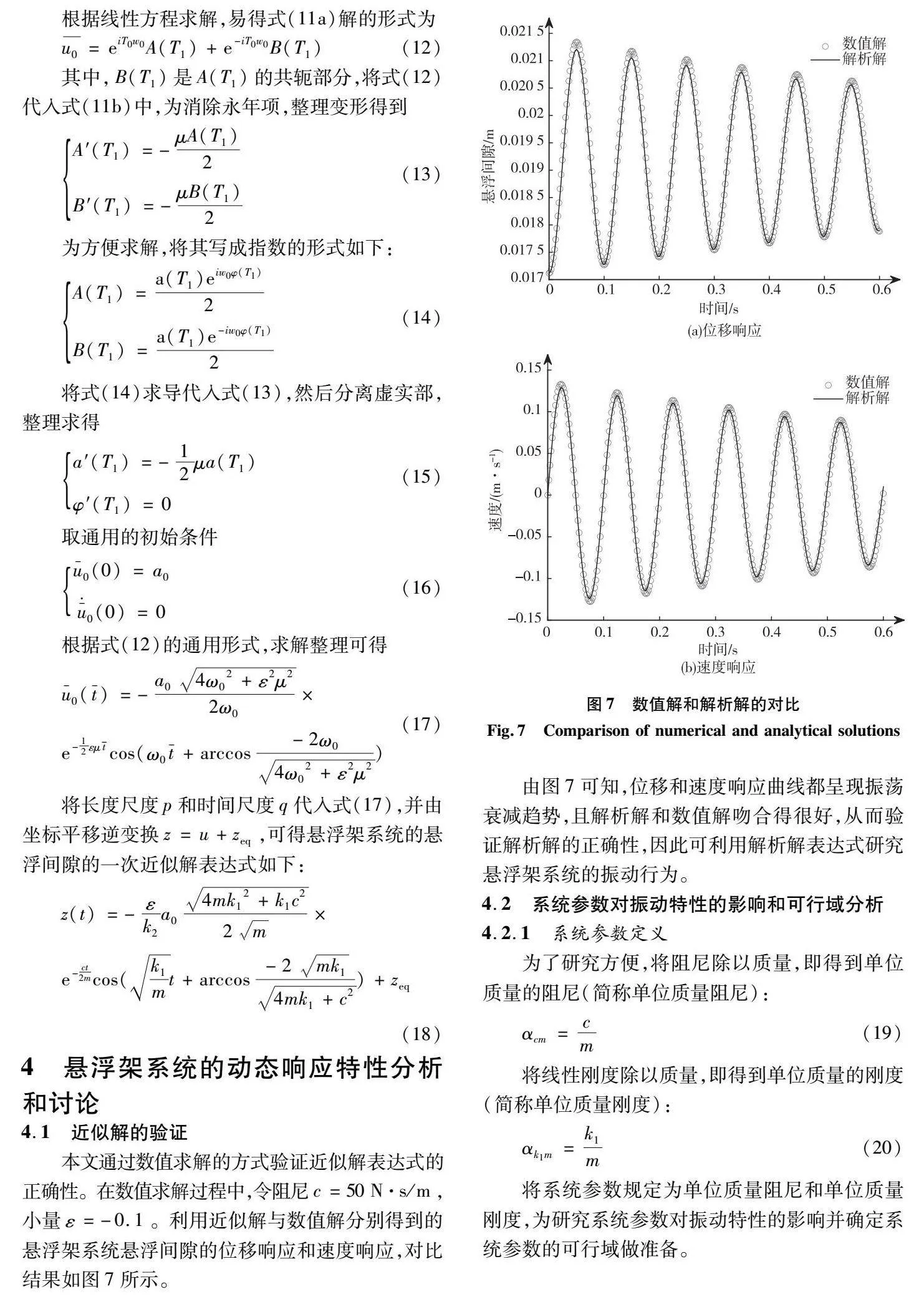
本文通过数值求解的方式验证近似解表达式的正确性。在数值求解过程中，令阻尼c=50N·s/m，小量ε=-0.1。利用近似解与数值解分别得到的悬浮架系统悬浮间隙的位移响应和速度响应，对比结果如图7所示。

由图7可知，位移和速度响应曲线都呈现振荡衰减趋势，且解析解和数值解吻合得很好，从而验证解析解的正确性，因此可利用解析解表达式研究悬浮架系统的振动行为。

4.2系统参数对振动特性的影响和可行域分析

4.2.1系统参数定义

为了研究方便，将阻尼除以质量，即得到单位质量的阻尼（简称单位质量阻尼）：

αcm=cm（19）

将线性刚度除以质量，即得到单位质量的刚度（简称单位质量刚度）：

αk1m=k1m（20）

将系统参数规定为单位质量阻尼和单位质量刚度，为研究系统参数对振动特性的影响并确定系统参数的可行域做准备。

4.2.2安全性指标

为了保证磁悬浮列车的安全运行，悬浮架系统的悬浮间隙需要满足磁悬浮标准中的动力学指标，即限定在一定范围内，可得

z（0）－zeq≤zstr（21）

式中：zstr为偏离平衡位置允许的最大振动幅值。

设初始时刻的位置达到最大振动幅值，由式（21）可得

εa0=k2zstrk1（22）

4.2.3衰减性指标

为了满足快速衰减的性能，规定在悬浮架系统第一次达到峰值偏离平衡位置的差值，即为最大超调量，需衰减到允许最大振幅的η（0<η<1）倍，这时需确定达到峰值的时间tp，由式（18）易得

cos（k1mtp+arccos－2mk14mk1+c2）=－1（23）

可得

tp=π－arccos－2mk14mk1+c2mk1（24）

由此将式（22）代入式（18），同时根据式（19）和（20）整理可得

zM=z（tp）－zeq=zstr4αk1m2+αk1mαcm22αk1m×e－αcm2αk1mπ－arccos－2αk1m4αk1m+αcm2（25）

根据式（25，由衰减性指标整理可得

f（αk1m，αcm）=4αk1m2+αk1mαcm2×

e－αcm2αk1mπ－arccos－2αk1m4αk1m+αcm2－2αk1mη≤0（26）

4.2.4舒适性指标

为了保证乘客的舒适性，磁悬浮列车的加速度需满足人体的承受能力，则悬浮架系统上的加速度需要限定在特定的范围内。由式（20）可以2次求导，并根据三角函数和公式，整理可得加速度表达式：

a（t）=－εa0（4mk12+k1c2）[16mc2k1+（c2－4mk1）2]8k2m2me－ct2m×

cosk1mt+arccos－2mk14mk1+c2－arccosc2－4mk116mc2k1+（c2－4mk1）2

（27）

则

a（t）≤－εa0（4mk12+k1c2）[16mc2k1+（c2－4mk1）2]8k2m2m

（28）

规定式（28）的上限为最大加速度amax，根据式（19）和（20）和（22）可得

amax=zstr（αcm2+4αk1m）4αk1m2+αk1mαcm28αk1m（29）

由于乘客乘坐的舒适性，要求最大加速度不应超过允许最大加速度amaxstr，则根据式（29）可得到磁悬浮列车系统参数应该满足

gαk1m，αcm=zstr（αcm2+4αk1m）×

4αk1m2+αk1mαcm2－8αk1mamaxstr≤0（30）

4.2.5分析和讨论

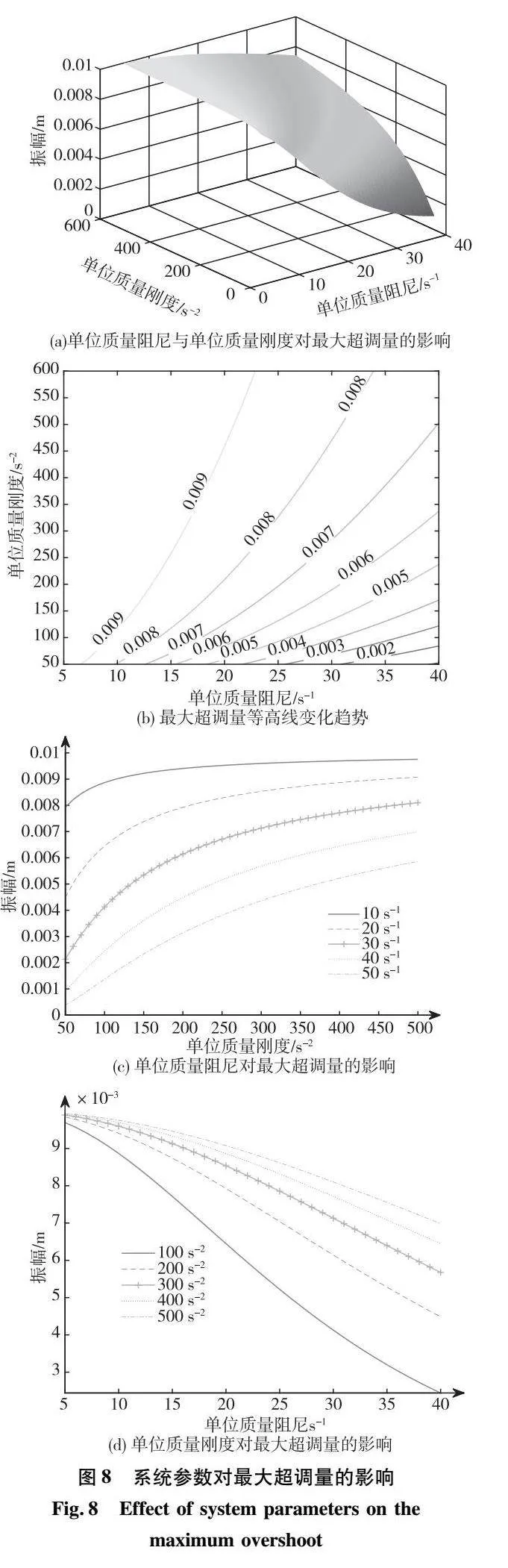
由式（25）可知，最大超调量受单位质量阻尼和单位质量刚度的影响，呈现非线性的关系。根据高温超导磁悬浮列车的悬浮架本体和铁轨之间的悬浮高度为10mm左右，两者间的距离偏离平衡位置的最大振幅为5mm；而高温超导磁悬浮列车的悬浮架本体和永磁轨道之间的悬浮高度为20mm左右，根据同样比例限值规定，后者的距离偏离平衡的最大振幅确定为10mm。由式（25）可得最大超调量与系统参数的关系，如图8所示。

由图8中（a）和（b）可知，最大超调量随单位质量阻尼的增大而减小，随单位质量刚度的增大而增大；由图8（c）可知，随单位质量阻尼的增大，最大超调量减小程度越来越快，且单位质量刚度越小，减小速度更快；由图8（d）可知，曲线整体呈上凸趋势，且随单位质量刚度的增大，最大超调量增大程度逐渐变慢，且单位质量阻尼越大，增大速度越来越慢。综上所述，单位质量阻尼是影响最大超调量的重要因素，次要因素是单位质量刚度。为了限制最大超调量，单位质量阻尼应取较大值，单位质量刚度应取较小值。

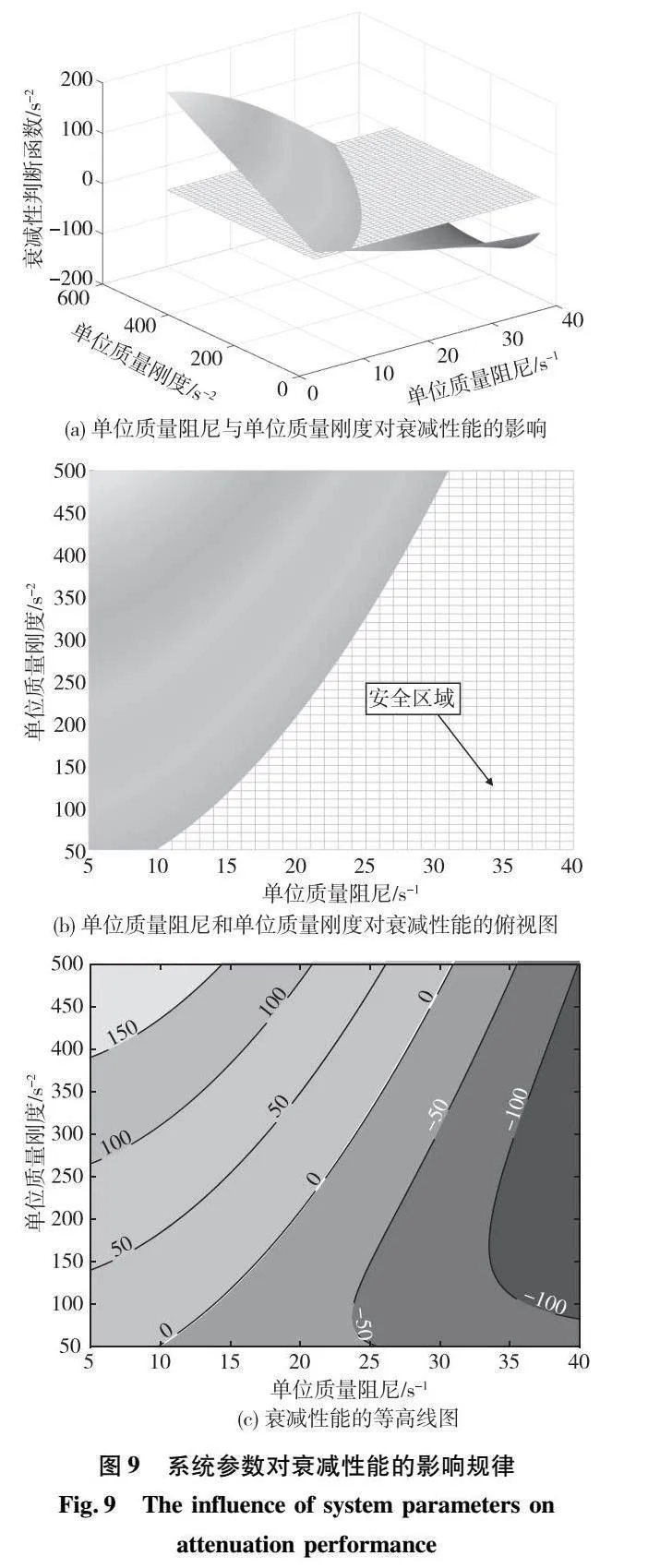
由式（26）可根据衰减性能指标得到单位质量阻尼和单位质量刚度需满足的可行域，根据式（26）中f（αcm，αk1m）的表达式，假定η等于0.8，得到满足衰减性能指标的范围，如图9所示。图9（a）中的彩色曲面在0横截面以上对应的系统参数均不满足衰减性能的标准，图9（b）和（c）中可观察到0标准线的位置，标准线以下为系统参数可行域，如图9（b）中浅绿色区域所示。

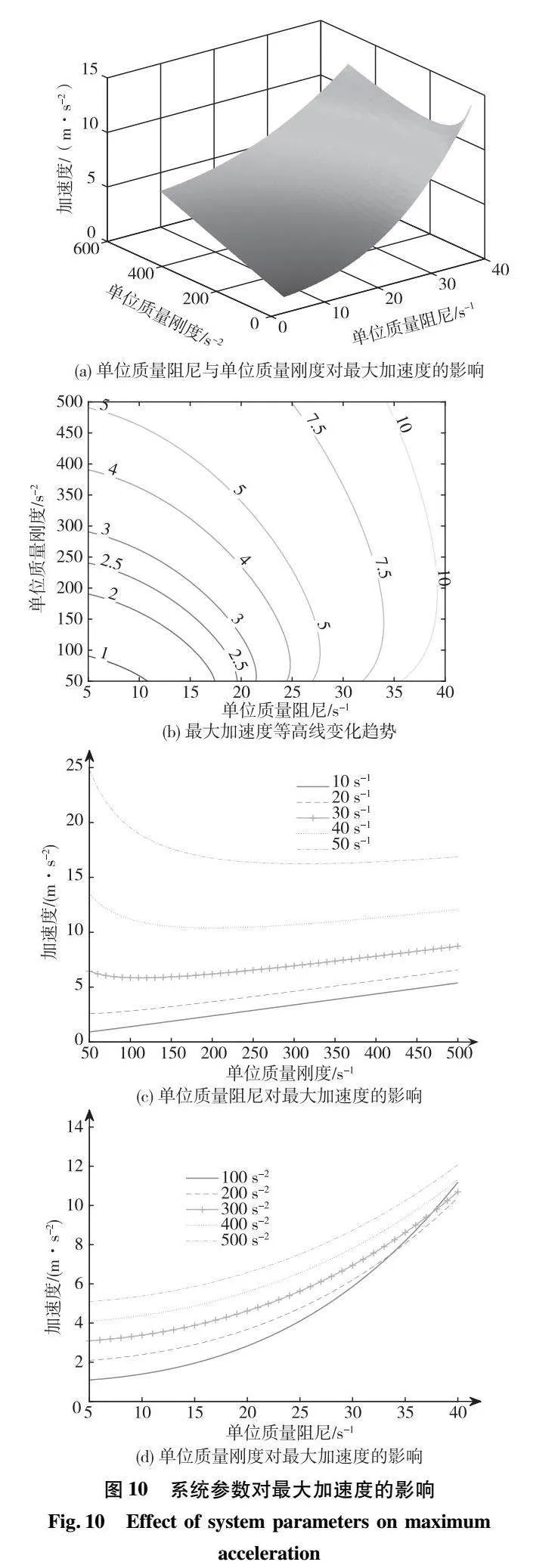
由式（29）可知，最大加速度受单位质量刚度和单位质量阻尼的影响，呈现出非线性的关系，由式（29）可得最大加速度与系统参数的关系，如图10所示。

由图10（a）和（b）可知，最大加速度随单位质量阻尼的增大而增大，随单位质量刚度先减小后逐渐增大；并且单位质量阻尼对其影响更显著；由图10（c）知，曲线整体呈下凹的趋势，表明随单位质量阻尼的增大，最大加速度增大程度越来越快；由图10（d）可知，在不同的单位质量阻尼下，单位质量刚度的变化趋势不同；单位质量阻尼较小时，最大加速度随单位质量刚度的增大而增大；单位质量阻尼较大时，随单位质量刚度的增大，最大加速度一开始呈明显的下降趋势，后逐渐增大，但增大趋势较缓慢。综上所述，影响最大加速度的重要因素是单位质量阻尼，其次是单位质量刚度。为了满足舒适性指标，限制最大加速度的大小，单位质量阻尼和单位质量刚度应取较小值。

由式（30）可根据舒适性指标得到单位质量阻尼和单位质量刚度需满足的可行域，根据式（30）中g（αcm，αk1m）的表达式，根据磁悬浮列车标准中的动力学指标，假定悬浮架系统上允许最大加速度等于2.5m/s2，得到满足舒适加速度的范围，如图11所示。图11（a）中的彩色曲面在0横截面以上对应的系统参数均不满足舒适加速度的标准，图11（b）和（c）中可观察到0标准线的位置，标准线以下为系统参数可行域，如图11（b）中黄色区域所示。

由图11可知，当单位质量阻尼较大时或单位质量刚度较大时，系统容易不满足最大加速度舒适性的许用标准。系统需要有合适的单位质量刚度和单位质量阻尼才能满足舒适性指标，由图11（b）和（c）可观察到系统参数的可行范围呈现近似的子弹头区域，要想满足舒适性指标，必须在可行域内部，即0标准线的左侧。为满足舒适性指标，单位质量阻尼和单位质量刚度不宜取太大。

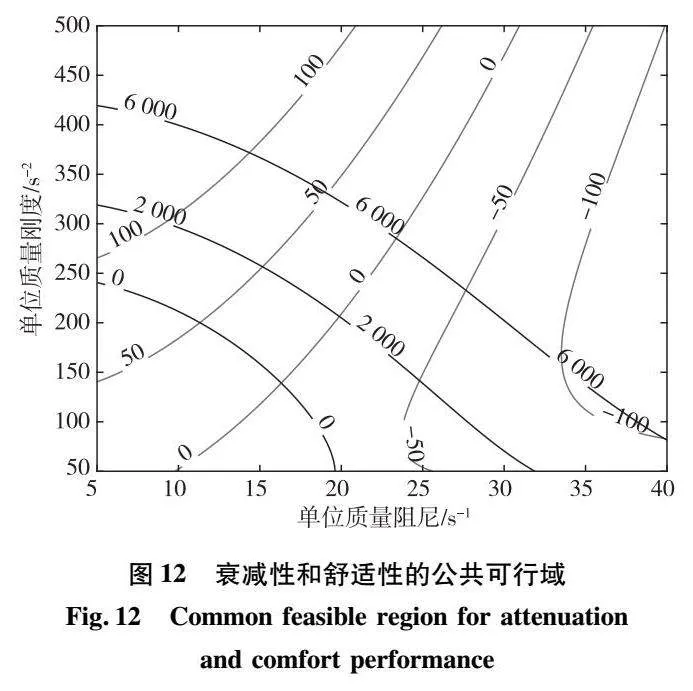
根据衰减性和舒适性两个指标得到系统参数需满足公共的可行域，使磁悬浮列车具有更好的动态性能。根据式（26）和式（30）中f（αcm，αk1m）和g（αcm，αk1m）均小于0，可得系统参数需满足的公共可行域，如图12所示。

由图12可观察到两个0标准线中间底部蓝色阴影区域的交集即系统公共的可行域，经计算可得到三个交点（9.8，50），（19.6，50），（16.3，139），当单位质量刚度和单位质量阻尼过大时，系统一定不

满足两个标准。需要注意的是当单位质量阻尼小于19.6s-1，但是单位质量刚度参数不合适时，也有可能不符合两个指标；同理，当单位质量刚度小于139s-2，但是单位质量阻尼参数不合适时，也有可能不符合两个指标，系统参数可行域近似为扇形区域，在参数设计时需要在阴影区域取值。

5结论

本文建立了高温超导钉扎磁悬浮列车的悬浮架系统的动力学微分方程，基于解析解分析了悬浮架系统自由振动运行规律，研究了系统参数对悬浮架系统最大超调量和最大加速度的影响，基于磁悬浮列车标准中的动力学指标提出了一种确定系统参数可行域的方法。主要结论如下：

1）利用多尺度法得到了悬浮架系统悬浮间隙解析解表达式，通过数值仿真的方式验证解析解的正确性。

2）利用解析解得到了系统的最大超调量和最大加速度解析形式，研究得到了最大超调量随单位质量阻尼的增大而减小，随单位质量刚度的增大而增大；最大加速度随单位质量阻尼的增大而增大，随单位质量刚度的增大先减小后增大，同时得到两者的重要影响因素均是单位质量阻尼，单位质量阻尼宜取小值，单位质量刚度宜取小值。

3）根据磁悬浮衰减性和舒适性两个动力性指标得到系统参数需满足的可行域，当单位质量阻尼大于19.6s-1或单位质量刚度大于139s-2时，系统一定不满足两个指标；更为重要的是研究表明可行域近似为扇形区域。

本文揭示了悬浮架系统在自由振动下的运动演化行为，为悬浮架系统的参数设计提供了理论指导。

参考文献：

[1]王家素，王素玉.高温超导磁悬浮列车研究综述［J］.电气工程学报，2015，10（11）：3-4.

［2］徐飞，罗世辉，邓自刚.磁悬浮轨道交通关键技术及全速度域应用研究［J］.铁道学报，2019，41（3）：40-49.

［3］邓自刚，张卫华.高温超导磁悬浮或将引发交通运输的大变革［J］.金融经济，2016，11（19）：42-43.

［4］HELLMAF，GYORGYEM，JOHNSONDW，etal.LevitationofamagnetoveraflattypeIIsuperconductor［J］.JournalofAppliedPhysics，1988，63（2）：447-450.

［5］PETERSPN，SISKRC，URBANEW，etal.ObservationofenhancedpropertiesinsamplesofsilveroxidedopedYBa2Cu3Ox［J］.AppliedPhysicsLetters，1988，52（24）：2066-2067.

［6］COOMBST，CAMPBELLA.Gapdecayinsuperconductingmagneticbearingsundertheinfluenceofvibrations［J］.PhysicaCSuperconductivity，1996，256（3/4）：298-302.

［7］COOMBST，CARDWELLD，CAMPBELLA.Dynamicpropertiesofsuperconductingmagneticbearings［J］.IEEETransactionsonAppliedSuperconductivity，1997，7（2）：924-927.

［8］TESHIMAH，TANAKAM，MIYAMOTOK，etal.Effectofeddycurrentdampersonthevibrationalpropertiesinsuperconductinglevitationusingmelt-processedYBaCuObulksuperconductors［J］.PhysicaCSuperconductivity，1997，274（1/2）：17-23.

［9］TESHIMAH，TANAKAM，MIYAMOTOK，etal.Vibrationalpropertiesinsuperconductinglevitationusingmelt-processedYBaCuObulksuperconductors［J］.PhysicaCSuperconductivity，1996，256（1/2）：142-148.

［10］HIKIHARAT，MOONF.Chaoticlevitatedmotionofamagnetsupportedbysuperconductor［J］.PhysicslettersA，1994，191（3/4）：279-284.

［11］HIKIHARAT，FUJINAMIT，MOONF.Bifurcationandmultifractalvibrationindynamicsofahigh-Tcsuperconductinglevitationsystem［J］.PhysicsLettersA，1997，231（3/4）：217-223.

［12］王晓融.高温超导YBCO块材在永磁导轨上方导向力的研究［D］.成都：西南交通大学，2003.

［13］MOONF，YANOVIAKM，WARER.Hystereticlevitationforceinsuperconductingceramics［J］.AppliedPhysicsLetters，1988，52（18）：1534-1536.

［14］勾艳凤.高温超导磁悬浮车环形线振动特性研究［D］.成都：西南交通大学，2015.

［15］肖玲，任洪涛，焦玉磊，等.YBCO超导体的磁悬浮力及其测量［J］.低温物理学报，1999，21（4）：317-320.

［16］DENGZ，ZHENGJ，SONGH，etal.Freevibrationofthehightemperaturesuperconductingmaglevvehiclemodel［J］.IEEETransactionsonAppliedSuperconductivity，2007，17（2）：2071-2074.

［17］LIUW，WANGJS，LIAOXL，etal.Influenceofthetrappedfieldonthelevitationperformanceofthemagnetizedbulkhigh-TcSuperconductor［J］.JournalofSuperconductivityandNovelMagnetism，2011，24（5）：1563-1569.

［18］张兴义，周军，周又和.高温超导体时效与记忆效应实验研究［J］.实验力学，2013，28（5）：572-579.

［19］胡博，林建辉，邓自刚.高温超导磁悬浮动态测控系统运动控制与数据采集部分的关键技术研究［J］.装备制造技术，2017，39（2）：1-5.

［20］李刚，刘坤，杨文姣，等.YBCO堆叠高温超导磁体的磁悬浮振动传递特性实验研究［J］.低温物理学报，2018，40（3）：8-12.

［21］杨文姣，马光同，QUEVALL，等.基于三维多物理场强耦合模型的超导磁悬浮振动特性［J］.科学通报，2019，64（31）：3255-3266.

［22］任晓晨，刘伟，庞鹏，等.空间高频交变磁场对超导块材悬浮力影响研究［J］.低温物理学报，2019，41（5）：355-360.

［23］陈楠，陈洋，孙睿雪，等.高温超导-永磁混合悬浮车基本系统的理论模型与实验［J］.科学通报，2020，65（9）：847-855.

［24］ZHANGML，SUNGX，LIUPF，etal.Researchonforcecharacteristicsandrunningperformanceofnoveltypehigh-temperaturesuperconductormagneticlevitationvehicle［J］.JournalofSuperconductivityandNovelMagnetism，2022，35（3）：635-646.

［25］张明亮，李明远，刘鹏飞，等.面向高温超导钉扎磁悬浮列车悬浮特性研究［J］.中国机械工程，2022，33（22）：2764-2771.

（责任编辑：于慧梅）

Abstract：

Thefreevibrationcharacteristicsofthesuspensionsystemofhightemperaturesuperconductingpinnedmaglevtrainswillaffectthesafetyandcomfortofpassengers，thusitisofgreatimportancetostudythefreevibrationofthesuspensionsystem.Thelevitationforcedatabetweenthehightemperaturesuperconductorscombinationandthepermanentmagnetguidewayiscollectedbytheexperimentaldevice，andtheempiricalformulaofthelevitationforceisobtained.Theverticalvibrationdynamicmodelofthesuspensionsystemisestablishedbasedontheempiricalformula.Themulti-scalemethodisusedtoderivetheapproximatesolutionofsuspensiongapresponse，andthecorrectnessoftheapproximatesolutionisverified.Basedonthesuspensiongapapproximationsolution，theexpressionsofmaximumovershootandmaximumaccelerationofthesystemarederived，andtheinfluenceofdampingpermassandstiffnesspermassofsystemparametersonmaximumovershootandmaximumaccelerationisstudied.Accordingtothetwodynamicindexesofattenuationandcomfortofmaglevstandard，amethodtodeterminethefeasibleregionofsystemparametersisproposed.Theresultsshowthatthedampingpermassshouldbelessthan19.6s-1，thestiffnesspermassshouldbelessthan139s-2，andthefeasiblerangeofsystemparametersshouldbeapproximatelysector-shaped.Theaimofthismanuscriptistoprovidethetheoreticalsupportfortheparameterdesignofthesuspensionsystem.

Keywords：

suspensionframesystem;levitationforce;multi-scalemethod;approximationsolution;feasibleregionofsystemparameters

收稿日期：2024-02-26

基金项目：河北省高等学校科学技术研究资助项目（ZD2022064）；国家自然科学基金青年资助项目（52205064）；河北省自然科学基金青年资助项目（E2021210065）；光电技术与智能控制教育部重点实验室（兰州交通大学）开放课题资助项目（KFKT2020-7）；牵引动力国家重点实验室（西南交通大学）开放课题资助项目（TPL2010）

作者简介：张明亮（1984—），男，副教授，博士，研究方向：机械系统动力学和磁悬浮技术，E-mail：zmlhit@126.com.

*通讯作者：张明亮，E-mail：zmlhit@126.com.