牛顿-莱布尼茨的微积分发明优先权之争(中)
2024-09-30陈学雷

中年牛顿的转变
牛顿在1685—1687年完成了旷世名著《自然哲学的数学原理》(简称《原理》,关于这一过程可参见笔者《苹果》一文)。然而在该书中他使用了传统的几何论证给出他的结果,并没有直接使用他的微积分方法——流数法。不过,在该著第一版中,牛顿提到了这一方法以及莱布尼茨:“十年前,在与技艺高超的几何学家莱布尼茨先生通信时,我指出我拥有一种求极大与极小、求曲线切线等的办法,这位名家回复说他也发现了这样的方法,并将他的方法透露给我。除了词句和记号外,这方法与我的几乎没有不同。”后来,当微积分发明的优先权发生争议时,牛顿一方认为这段话说明牛顿早已发明了微积分方法,而莱布尼茨一方则认为这段话说明牛顿承认莱布尼茨发明了微积分方法,以及他收到过莱布尼茨关于微积分方法的说明。两人冲突爆发后,牛顿在《原理》后来的版本中删去了这段话。
1687年,牛顿完成了《原理》后,性格似乎发生了某些改变。在此之前,牛顿只专注于他的研究,对此之外的事几乎毫不关心,也很少与人交流。但是这一年,《原理》还在印刷中,牛顿就参与了一项重大政治活动。1685年英王查理二世(CharlesⅡ)去世,詹姆斯二世(JamesⅡ)继位。自1534年亨利八世(HenryⅧ)因为离婚与罗马天主教决裂后,英国国教成为英国的主流宗教,但仍有一部分人信奉罗马天主教,詹姆斯二世就是如此。他上台后,就试图将一些天主教徒任命到高位上,最终目标是使英国回归天主教。1687年,他特旨要求剑桥大学给一位天主教修士授予学位,而免去一切考试和宣誓。这里的关键是,按照英国议会通过的法律要求,获得学位者需要宣誓承认国王是教会的最高权威,而这是遵奉教皇为最高权威的罗马天主教徒不接受的。此前,国王也时常颁发各种特旨,让大学对某些人免去常规的义务,比如牛顿本人以前就是靠这种特旨而免去了担任圣职的义务。但是,这次国王的特旨却遭到了剑桥大学师生的普遍反对,因为从当时的情况看,国王是准备让剑桥大学授予该修士学位后就任命他管理剑桥大学。有点出人意料的是,一向埋首学问的牛顿这次竟然是抗议活动的领头人之一,是向国王请愿团的骨干成员,并撰写了宣传小册子。牛顿虽然并不完全认同英国国教会,但是他显然更不能接受天主教会。詹姆斯二世撤了当时剑桥大学副校长的职(当时剑桥大学正校长是挂名的,副校长是实际负责人),并对请愿团成员发出威胁,但即便如此,请愿团和剑桥大学最终也没有屈服。詹姆斯二世向各个重要位置大批任命天主教徒的做法激起了国内的强烈反抗,先后爆发了数次起义。次年(1888年),詹姆斯二世被迫流亡法国,而他信奉新教的女儿玛丽(Mary)和女婿威廉(William)被议会选为新的统治者,这就是英国宪政历史上非常著名的“光荣革命”。牛顿于是一举成为反抗詹姆斯二世的英雄,被选为代表剑桥的两位议会议员之一。牛顿在议会并不活跃,几乎从未发言,但他与此时当政的辉格党人高层建立了密切关系,特别是毕业于三一学院、此时负责财政的蒙塔古(C. Montague,后成为哈利法克斯伯爵)与牛顿成为好友。托他的关系,1696年牛顿被任命为英国造币厂总监。

很多人都知道牛顿晚年在造币厂任职,不过并不了解其历史背景,以为牛顿是有什么特殊的经济理论或专业才能而被任命的。其实,造币厂总监一职当时被视为一种待遇优厚的闲职,是蒙塔古等辉格党人给牛顿的照顾或酬报。这一职位的收入(每年400英镑)远高于牛顿作为剑桥大学卢卡斯讲座教授的薪金(每年100英镑)。剑桥虽然给牛顿提供了一个自由的研究环境,但此时的剑桥在学术上并不活跃,而牛顿对教学显然也没什么兴趣。年过半百的牛顿创造力也开始下降,不想再埋头做研究,所以决定离开剑桥而去造币厂任职。不过,牛顿到任后并未像之前的总监那样坐享清福,而是主动开始承担其大量管理工作。1699年,前任厂长去世后牛顿继任了厂长职位(年薪500英镑+铸币利润分成)。在造币厂的职位上牛顿很认真地工作,为英国铸造了大量高质量硬币,还负责抓捕制造假币者,在这方面他毫不留情,把多个抓获的造假币者送上绞刑架。后来蒙塔古承认,尽管他最初只是想给牛顿一个领薪水的闲职,但幸亏有牛顿对铸币工作的高效管理,其货币政策才最终得以推行。牛顿被封为爵士也是由于他在造币厂的工作而不是由于他的科学贡献。

中年莱布尼茨
莱布尼茨到汉诺威后主要任务是管理图书馆和编撰不伦瑞克(Brunswick)家族的历史,这使他获得了资金可以走访欧洲各地,从各处的图书馆、修道院中查找相关资料,这在当时的学者中是很难得的经历。莱布尼茨的家族史研究颇具实用价值——由于他的一系列历史考证证明了这一家族的高贵血统,使他们最终获得了选帝侯也就是选举神圣罗马帝国(德国)皇帝的资格。不过,撰写这一漫长的家族史耗费了莱布尼茨大量的时间精力,直至他去世也未能完成,而且由于他迟迟未能完成这一历史著作,他的几任雇主都对他不太满意,倒是汉诺威宫廷中的聪明女士们都很喜欢这位渊博的学者。不过,最终该家族地位的真正提升并不来自莱布尼茨的历史考证,而是来自公爵夫人,她是英国皇室后裔,在斯图亚特王朝绝嗣后,她的儿子作为新教徒被英国议会选中继承了英国王位,1714年成为英王乔治一世(George I) 。该家族此后成为英国王室并持续至今,只是后来把名字改为听起来更英国化的“温莎王朝”。
在学术方面,莱布尼茨进行了哲学、语言学等多方面的研究和写作,这使他在后世尤其以哲学家著称。在数学方面,除了微积分之外,莱布尼茨还发明了二进制、行列式,并开启了位置分析(拓扑学前身)。不过,莱布尼茨也有一些失败:在汉诺威他主动提议用风力驱动为一座矿山排水,以解决在旱季原来的水力驱动无法运行的问题,还设计了风车,但这一计划最后失败了,使莱布尼茨损失了一大笔钱。但他也因此走访了许多矿山,成为地质和化石研究的先驱。
总之,莱布尼茨知识渊博,人脉广阔,学术地位不断上升。莱布尼茨对组织学术团体也很感兴趣,说动普鲁士国王资助创办柏林学会,身在汉诺威的莱布尼茨也成为其首任会长。彼得大帝访问汉诺威时专门与他交谈。他发表的微积分尤其影响广泛, 很多人从他这里学到了微积分,并习惯采用了他的术语(“微分”“积分”)和符号。
牛顿微积分的公开发表
1693年,牛顿的微积分结果也终于公开发表了,不过发表这一结果的还不是牛顿本人,而是老一辈英国数学家沃利斯(J. Wallis, 1616—1703),学生时代牛顿曾学习过他的著作。
这一时期的英国还远不是后来称霸全球的日不落帝国,与当时欧洲文明的中心法国相比各方面都差一大截,因此不少英国人很在意别人的眼光。沃利斯就是这样,他特别注重宣扬英国学者的成就。他曾从柯林斯(J. Collins)那里知道牛顿的微积分成果,眼看莱布尼茨的著作风行天下,世人都只知道微积分是莱布尼茨发明的,老沃看不下去了。于是他征得牛顿同意,在他1693年出版的一本教科书的附录中发表了牛顿之前写的文章,介绍了流数法。


为何此前坚决不肯公开发表这一结果的牛顿此时又同意发表了呢?可能牛顿自发表了《原理》之后自信心大增,性格与以往不同。笔者猜还有一个因素,就是莱布尼茨的微积分也并没有受到牛顿预想中的攻击,反之广为流行并受到好评。沃利斯在书中指出牛顿和莱布尼茨的微积分只是术语和记号不同,实质是完全一样的。老沃在书中甚至认定牛顿的符号更好,这只能说是用力过猛了,后来几乎所有的学者都认为莱布尼茨的符号更便利。沃利斯在书中说,牛顿在1676年给莱布尼茨的信中就曾提到这一方法,意思就是牛顿的发明更早,不过他也没有否认莱布尼茨的独立发明。沃利斯的这一叙述还是比较符合历史事实的。
莱布尼茨听说沃利斯的书后,倒也没有否认牛顿的独立发明权。此时,他处在有利的地位上,毕竟是他首先公开发表了微积分。虽然英国人现在声称牛顿更早发明了微积分,但在莱布尼茨的理论流行之前没有公开发表过,其可信度大打折扣。对于英国人的这种说法一些欧陆学者颇为怀疑,如果牛顿那么早就发明了微积分,为什么他在多年里都不公开发表?莱布尼茨的朋友约翰·伯努利(Johann Bernoulli, 1667—1748)就怀疑,牛顿其实是从莱布尼茨的文章那里才学到了微积分,之前牛顿也许只是提出了“流数”的概念,而真正的微积分还有具体的“算法”,牛顿未必都掌握了,否则牛顿为什么在他的《原理》中不使用流数法呢?仅仅提个概念就把微积分的发明权拿走,这也太便宜牛顿了吧?不行,得想个办法。

最速降线
伯努利是数学史上著名的家族,出了多位学者,不过他们喜欢反复使用几个名字,让人很容易搞混。这其中,在微积分上做出主要贡献的是约翰·伯努利。他想出一个办法:他要出个微积分难题,看看牛顿能否做出来,这就是历史上非常著名的最速降线问题。
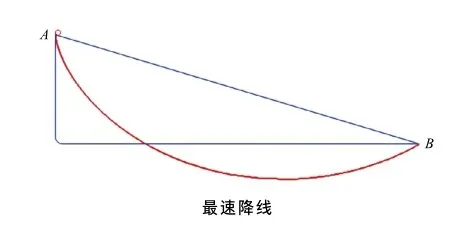
同一平面上的两点A, B,A在B的斜上方,那么有无数多条曲线连接A和B。设想一质点在重力作用下从A滑向B,忽略摩擦,什么样的曲线可以使其最快滑到B?
A和B之间最短的是连接这两点的直线,但沿直线滑下去并不是用时最短的,因为如果一条曲线一开始的部分比直线AB更陡一些,那么质点就会较早地加速到更高的速度,虽然路程长一些,却可以更快抵达B点。但最短的线到底是什么呢?解决这一问题的方法是变分法,这是微积分中比较高级的技巧。后来,约翰·伯努利的学生欧拉发展了系统的变分法,而这道题的答案是,最速降线其实是一种旋轮线——想象我们标记一个轮子边上的一点,那么轮子滚动前进时这一点画出的轨迹就是旋轮线。
当然,约翰·伯努利没法直接对牛顿说“老牛,我不信你真会微积分,来做做我的考试题”。所以,1696年,他在《学者学报》(Acta eruditorum)上公布了这个面向全欧洲学术界的挑战题,限期6个月到当年年底。同时他也专门给牛顿、沃利斯等英国人寄去了这一挑战题。不过,一开始牛顿等人并未理会。于是,他又再次发文给出挑战,将挑战延期了几个月,声称到1697年复活节会公布自己和莱布尼茨的解答,并且写了一段话,赤裸裸地将能否解出这一题目与是否真正掌握了微积分联系起来。这次牛顿回应了。据说,1697年1月某日,牛顿在造币厂辛苦工作了一天后,凌晨4点才回到家中,看到了寄来的题目,马上开始做,用了2小时,赶在早班邮递员到来时写出答案寄走了,而约翰·伯努利本人当初是花了两个星期才做出来的。牛顿寄给约翰·伯努利的答案并没有署名,但约翰·伯努利“从爪印中认出了狮子”。
按时完成挑战题目的只有牛顿、莱布尼茨、伯努利兄弟和他们的学生洛必达(de L’Hopital)侯爵(今天学习微积分的学生都知道的“洛必达法则”其实是约翰·伯努利给出的,但发表在洛必达撰写的微积分教科书中)。挑战结果公布后,莱布尼茨感叹,做出这道题目的人都在他意料之中,都是真正深入理解微积分的人,除了牛顿外,就是他自己和他的弟子们。他这话惹怒了一个人,纷争开始了。
争端初起
一开始,牛顿和莱布尼茨彼此默认各自独立发明了微积分。但是,这种和平很快就被打破。1699年,伯努利的瑞士同乡、莱布尼茨的师弟、牛顿的疑似同性恋人尼古拉·法蒂奥·德·杜里耶(Nicolas Fatio de Duillier, 1664—1753)开始公开质疑莱布尼茨剽窃了牛顿的结果。法蒂奥少年时代就在天文、光学等方面发表了多篇论文,他给出了黄道光的正确解释——黄道面上的碎石和尘埃反射的太阳光。后来他向惠更斯学习数学,从这个角度说可以算莱布尼茨的师弟,惠更斯对他颇为欣赏并介绍他与莱布尼茨通信,但不知何故这二人话不投机。另一方面,法蒂奥倒是和牛顿一见如故。
有人怀疑牛顿是同性恋,这是因为他和法蒂奥一度关系很亲密,有段时间他们经常在一起参加各种活动,法蒂奥还说要帮助牛顿修订《原理》。法蒂奥有一次生病以为自己将不久于人世,于是给牛顿写了封信,牛顿回信口吻非常亲密和关切,表示要和他住在一起并亲自照料他,这在牛顿一般是客套而冷淡的通信中可谓绝无仅有。但是不知何故,1693年后,二人的关系突然疏远了。而也就在这一时期,牛顿经历了一次精神崩溃,在长时间失眠后写了胡言乱语的绝交信给他的好友、英国经验主义哲学家洛克(J. Locke, 1632—1704)和著名日记作者、英国海军主管佩皮斯(S. Pepys, 1633—1703),不过后来牛顿逐渐恢复了正常。所以有人猜测,法蒂奥是牛顿的同性恋人,而牛顿精神崩溃与二人关系破裂有关。不过,也有学者认为这种猜测属于捕风捉影,二人的关系可能被过度解读了,甚至牛顿的精神崩溃是否与二人关系有关都难以确定。由于缺乏更多史料,这是一桩难以定论的悬案。总之,法蒂奥后来逐渐淡出了科学圈,成为一个小教派的传教者,不过在此之前,他首先开启了微积分发明优先权之争。
法蒂奥也解出了最速降线问题,但没赶上截止期。莱布尼茨认识他,却没把他列入精通微积分、有可能解出此题的人选之内,这让他感到自己被轻视了。1699年法蒂奥出版了一篇专著,给出了自己的解答。他声称早在1687年,自己在读到莱布尼茨的1684年论文前,也独立地发明了微积分,虽然时间比莱布尼茨稍晚。不过法蒂奥接着说,他在认识牛顿后发现,牛顿才是微积分的第一发明者,而且牛顿非常谦虚,不像莱布尼茨那样到处宣扬自己。他在文中暗示莱布尼茨是从牛顿那里“借走了”流数法,变成他的微积分。法蒂奥此时已和牛顿疏远了6年,但终其一生他一直对牛顿崇敬有加。

莱布尼茨通过沃利斯给皇家学会写信回击法蒂奥,说学者们应该相互尊重,而不是像泼妇们一样互相指责和争吵。莱布尼茨声称他对牛顿极为尊重,但在他1684年发表第一篇微积分论文时根本没听说过牛顿的流数法,何谈“借走了”牛顿的流数法?
莱布尼茨说的是否是真话呢?此前,牛顿在1676年给他的两封信中曾暗示自己有一种数学方法,事后看其实就是流数法或者说微积分,不过牛顿并没有明确地说出来。但是莱布尼茨还在柯林斯那里读到过牛顿的《分析》(见本文上篇),按说他应该是知道牛顿的微积分发明的,否则莱布尼茨当年回信时也不大可能把自己的微积分结果告诉牛顿。不过,莱布尼茨当时的关注点是无穷级数,在匆匆的阅读中对论文中关于微分和积分的部分并没有太在意,多年之后遗忘了也不是完全没有可能。而且,在《分析》中牛顿并没有用他后来使用的“流数”等术语,所以莱布尼茨说他此前没有听说过流数法也说得通。但另一方面,莱布尼茨此时也有很强的动机否认当年已知道牛顿发明了微积分,因为承认这一点不仅将使他沦为第二发明者,而且还会被质疑为何他的1684年论文只字不提牛顿。此时,柯林斯早已去世,这件事也只有莱布尼茨自己知道,他连好友约翰·伯努利也没有告诉。因此,莱布尼茨在这封信中的说法很可能并不完全诚实。
不过,莱布尼茨也没有否认牛顿独立于他发明了微积分。莱布尼茨在给沃利斯的信中指出,牛顿在《原理》中也肯定了他独立地发明了微积分,因此莱布尼茨断言法蒂奥对他的指责牛顿都不会同意。的确,牛顿在此次争议中一言未发。这场争论的结果似乎是,双方各自默认对方独立发明了微积分。
莱布尼茨的匿名书评
也在1699年,沃利斯又出版了一本书,这次书里又附上了牛顿1676年通过奥登堡(H.Oldenburg)发给莱布尼茨的那两封信。在此之前,虽然牛顿在一些场合提到过他和莱布尼茨1676年写信交流的事,但别人并不清楚他们到底交流了什么,有人甚至误以为牛顿从莱布尼茨那里学到了微积分,而这些信件的公布以及其中字谜的解密清晰地表明了牛顿的优先权。这些信件当年通过奥登堡转发,在皇家学会中留有存档,为牛顿提供了客观证据。沃利斯在出版这些信件前征得了莱布尼茨同意,不过莱布尼茨的一些友人忧心忡忡,对莱布尼茨说英国人是要把这一发明的光荣从莱布尼茨手中夺走。接着,又有几位英国学者相继出版了关于牛顿流数法的著作,都声称牛顿的发明具有优先权。这些对莱布尼茨作为微积分发明者的地位构成了挑战,莱布尼茨对牛顿的态度此时开始发生变化。
牛顿这边,1703年老对手胡克去世了,牛顿重返皇家学会,随即被选为皇家学会会长,从此学会的实权也从秘书长转移到会长。此时皇家学会有所衰落,定期会议的内容相当无聊,牛顿打算重整学会,使其再度辉煌,为此牛顿每次都亲自出席并主持学会会议。不用再担心老对手胡克攻击的牛顿此时也出版了他的《光学》,并在书的附录中发表了他撰写的两篇数学论文,其中《曲线的求积》一文给出了流数法的完整阐述。
针对牛顿的这一著作,莱布尼茨于1705年在《学者学报》上匿名发表了一篇书评。尽管对牛顿《光学》的总体评价还算正面,但对于这一附录,其中写道:“代替莱布尼茨的微分,牛顿先生如他一贯的那样使用了流数……他优雅地在《原理》以及其后的其他著作中都使用了这一方法,正如法布里在他的《几何简介》中用他的运动法代替卡瓦列里的无限小一样。”尽管不承认自己是作者,但莱布尼茨后来解释说,这里提到法布里(H. Fabrius, 1607—1688)和卡瓦列里(B. F. Cavalieri, 1598—1647)这两位之前的数学家,是因为他们使用的术语分别类似于牛顿的“流数” 和莱布尼茨的“无穷小”,如果是这样,表面上看这一评价似乎没什么特别。但是,当时的数学家都知道,法布里剽窃了卡瓦列里,所以这也可被理解为讥讽牛顿剽窃了莱布尼茨。
那么,莱布尼茨是否只是在这篇书评中一不小心用词不当造成误会呢?不是的。在这一时期发表的多篇匿名评论中,莱布尼茨针对流数法以及牛顿的学说都给出了一些批评或贬低。如果说,这些还勉强可以辩解只是不留情面的学术批评的话,他还让人在一本书中发表了一个牛顿《原理》第一版中的错误清单,假托是已经去世的惠更斯写的。其实,这个错误清单是牛顿自己为了在《原理》第二版中修订而总结的,经由法蒂奥之手流传到荷兰,并最终传到莱布尼茨手中,显然托名发表《原理》的错误清单也是有意识地打击牛顿学术声望的一招。
莱布尼茨和牛顿此前虽然关系疏远,但显然两人都知道对方的学术水平,在公开场合也总是彼此互相称赞,莱布尼茨更是高度公开赞誉牛顿。据说,某次普鲁士王妃问莱布尼茨牛顿的数学如何,莱布尼茨说如果把有史以来的数学发现排在一起,牛顿的发现要占一大半。莱布尼茨对牛顿独立发明微积分也并未公开提出质疑,那么他为何要在匿名书评中搞这些小动作呢?这种心理值得分析。也许莱布尼茨不甘放弃自己微积分最早发明者的地位,法蒂奥对他的攻击更使他反感牛顿,因而内心深处有贬低牛顿的欲望。莱布尼茨开始匿名发表一些批评或贬低牛顿的评论,可能他觉得反正是匿名的,牛顿追究不到自己头上。但是,莱布尼茨似乎有点一厢情愿,众所周知他是《学者学报》的创办者之一,而且这些评论根据其内容和受益者很容易被猜出是他写的,而这招致牛顿一方的报复是迟早的事,双方的关系开始恶化。
[1]Whiteside D T, eds. The mathematical papers of Isaac Newton, vols 1-8. Cambridge: Cambridge University Press, 1968.
[2]Newton I. The Principia, Mathematical Principles of Natural Philosophy. Translation by Cohen I B and Whitman A, guide by Cohen I B. Oakland: University of California Press, 1999.
[3]Westfall R. Never at Rest, a biography of Isaac Newton. Cambridge: Cambridge University Press, 1980.
[4]Rupert Hall A. Philosophers at War, the quarrel between Newton and Leibniz. Cambridge: Cambridge University Press, 1980.
[5]Bardi J S. The Calculus Wars, Newton, Leibniz, and the Greatest Mathematical Clash of All Time. New York: Thunder’s Mouth Press, 2006.
[6]Antognazza M R. Leibniz, An Intellectual Biography. Cambridge: Cambridge University Press, 2009.
关键词:微积分 牛顿 莱布尼茨 ■
