基于设备驱动和实质路径的逆序柔性综合调度算法

摘 要：现有的柔性综合调度算法大多正向调度工序且按短用时策略为工序选择加工设备，需要考虑工序的多个紧前工序约束条件且可能会造成同设备工序串行加工而延长产品完工时间，针对这些问题，提出了一种逆向调度工序的柔性综合调度算法。提出的算法首先构造逆置的工艺调度模型；接着采用短用时策略为设备选择预调度工序；驱动时刻，根据备选工序集中预调度工序存在的三种情况，分别采取三种不同的方式对工序进行调度。实例表明，该算法有效地提高了柔性综合调度的并行处理效率和设备利用率，缩短产品制造时间。

关键词：柔性综合调度；设备驱动；实质路径；逆序

中图分类号：TH165 文献标识码：A 文章编号：2096-4706（2024）14-0152-05

Reversed Flexible Integrated Scheduling Algorithm Based on

Device Driving and Essential Path

GUI Zhongyan1， ZHANG Zhen2， WANG Qian3， JIANG Leilei4

（1.School of Computer Science and Technology， Heilongjiang University， Harbin 150080， China; 2.Department of Information Technology， Sichuan Business Vocational College， Chengdu 610091， China; 3.School of Data Science and Technology， Hei-longjiang University， Harbin 150080， China; 4.Department of Safety Production， Jiusan Grain and Oil Industry Group Co.， Ltd.， Harbin 150090， China）

Abstract： The existing flexible integrated scheduling algorithms mostly schedule the procedures in the forward direction and adopt short-time strategy to select the processing devices for the procedures. It needs to consider the multiple constraint conditions of pre-process procedures and it may lead to serial processing of procedures on the same device thus prolong the completion time of the product. Aiming at these problem， this paper proposes a flexible integrated scheduling algorithm for reverse scheduling procedures. The proposed algorithm firstly constructs a process scheduling mode with reverse structure. Then short-time strategy has been used to select pre-scheduling procedure for devices. At the driving moment， this paper uses three different ways to schedule the procedures according to the three situations of the pre-scheduling procedures in the alternative procedures set. Examples show that the proposed algorithm effectively improves the parallel processing efficiency and the device utilization ratio of the flexible integrated scheduling， and the product processing time has been reduced.

Keywords： flexible integrated scheduling; device driving; essential path; reversed

DOI：10.19850/j.cnki.2096-4706.2024.14.031

收稿日期：2024-01-14

0 引 言

柔性车间调度问题是对传统车间调度问题的扩展，柔性加工工序具有多个可加工设备，更符合实际生产情况[1-4]。近年来，针对柔性调度优化问题的研究日益增多，相关专家学者已经取得了一定的成果[5-6]。例如，文献[7]提出一种分布式的柔性综合调度算法，该算法首先为产品构造正向调度的工艺树模型，再按照短用时策略为可柔性加工工序确定加工设备，将柔性综合调度问题转化为综合调度问题，然后采用拟关键路径法自底向上对工艺树中的工序进行调度，获得了较好的调度效果。但由于该算法是由工序找设备，即将工序调度到设备上加工时，需要在相应的设备上为工序寻找尽早加工结束的空闲时间段，不仅需要一定的比较空隙操作，而且当空闲时间段小于工序加工时间时，会出现工序延迟加工的情况。同时，该算法只采用短用时策略为柔性工序选择对应的加工设备，可能出现多个工序选择的最短加工用时设备为同一个设备的情况，导致该设备被安排大量工序串行加工，形成瓶颈设备，影响产品的加工制造效率。

为了避免以上算法由工序寻找加工设备过程带来的大量比较操作和工序延迟加工等问题，本文采用设备驱动策略[8-9]求解柔性综合调度问题。设备驱动策略是由设备寻找可调度工序，设备一旦空闲，便寻找可调度工序加工，无须比较空闲时间段操作，不会出现空闲时间段过小而导致产品延后加工的问题。但考虑到空闲设备驱动时刻，某空闲设备上可能会出现大量预调度工序排队等待串行加工的情况，因此，本文在驱动时刻采用了动态实质短路径策略[9-10]，解决大量工序等待加工时如何选择调度工序的问题。同时，为了更好地实现工序间的并行处理，当某一空闲设备上不存在预调度工序时，遵循设备尽量忙原则，从可调度工序集搜索加工设备为该空闲设备的工序加工。最后采用实例将本文算法与文献[7]中的算法进行对比，以说明本文算法的优越性。

1 问题分析

以往的调度算法大多是按照产品工艺树的加工顺序，自底向上对产品进行调度，优先调度子节点工序，再调度父节点工序[7]。由于多个当前节点（子节点）对应一个后继点（父节点），因此在自底向上方式中，当前节点和后继节点是多对一的调度关系，这种多对一的关系使得后继节点工序必须在所有当前节点工序全部调度完毕后才能被调度。由于当前节点的调度是比较零散的，开始加工时间和加工时长都是不固定的，这会影响后继节点工序的开始时间。如此循环下去会影响整个产品的加工时间。

当把产品工艺树逆置后，优先调度父节点工序，再调度子节点工序，当前节点（父节点）和后继节点（子节点）是一对多的关系，当前节点工序被调度完毕后，其任意后继节点均可开始加工，所以当前节点较早地加工完毕时，其多个后继节点也可以较早地并行加工处理，从而缩短总的加工时间。因此，有必要采用逆序方式自顶向下对工艺树中的工序进行调度。

1.1 相关概念

逆序柔性综合调度：逆序构建柔性综合调度产品的加工工艺树，再按照新的约束关系顺序对工序进行调度。

预加工设备：采取短用时策略为每道工序确定的加工设备。

预调度工序：预加工设备上的可调度工序。

可调度工序集：紧前工序数为0的工序组成的集合。

备选工序集：设备驱动时刻，某一空闲设备的预调度工序组成的集合。

1.2 数学模型

设N为工序数，D为加工设备数，Tmk为设备m上第k道工序的驱动时刻，tmi为设备m上第i道工序的加工时间，t′im为可柔性加工工序i在设备m上的加工时间。本文研究问题的数学模型描述为：

T = min{max{Tmk}}（1≤k≤N） （1）

tmi = min{t′im}（1≤m≤D） （2）

tmk = {Hmk = min{ （Lmj + tmi）， （Lmi + tmj}}-{Lmk} （3）

Tm（k+1）≥Tmk + tmk （4）

式（1）为目标函数，表示最小化最后完工时间；式（2）为通过短用时策略确定设备m的预调度工序；式（3）为采用动态实质短路径策略确定空闲设备m的加工工序。其中Lmi为设备m的备选工序集中最长路径上的预调度工序i的路径长度，Lmj（ j = 1，2，…，n-1）为m的备选工序集中其余预调度工序的路径长度，将最短路径上的预调度工序的加工时间赋值给tmk。式（4）为驱动时刻满足的约束关系。

2 调度策略设计

2.1 调度策略

研究加工和装配同步处理的柔性综合调度算法，就是为可同时在多个设备加工和装配处理的工序选择合适的加工设备，在满足工序间前后约束关系的前提下，使产品尽早加工结束。本文研究的调度问题满足文献[9]中描述的约束条件，并使用了以下调度策略。

2.1.1 短用时策略确定预调度工序

设工序Pi可在D个设备上加工，加工时间分别为{gi1，gi2，…，giD}。确定Pi的加工时间tmi = min（gi1，gi2，…，giD），即选择加工用时最短的设备m为Pi的加工设备。对设备m而言，某一驱动时刻，当Pi成为可调度工序时，Pi即为设备m的预调度工序。

2.1.2 空闲设备驱动策略

建立由设备集、备选工序集、可调度工序集、加工工序集和事件队列构成的调度系统[8]。驱动时刻，系统根据事件队列中出现的事件对设备集和工序集进行处理。

2.1.3 动态实质短路径策略

当空闲设备m存在多个（假设x个）预调度等待加工时，选择其中最长路径Lmi上的预调度工序pi作为计划调度工序，将pi分别与其余x - 1个工序pj（ j = 1，2，…，x - 1）两两交叉放到对方路径之前计算实质路径长度，选取路径长度最小值Hmk = min{Lmi + tmj，Lmj + tmi}（ j = 1，…，k，…，x - 1）为实质短路径长度，优先调度实质短路径Hmk上的预调度工序pk。当存在多条长度相等的实质短路径时，调度其中加工用时多的预调度工序。

2.1.4 设备尽量忙原则

驱动时刻，当空闲设备m的备选工序集不存在预调度工序但可调度工序集存在可调度工序时，搜索可调度工序集是否有可在m上加工的可调度工序，如果有一个，则确定其为m上的加工工序；如果有多个，则选择其中路径最长的可调度工序为m上的加工工序，如果不存在，则m继续处于空闲状态。

2.2 调度方案设计

首先根据产品加工顺序的工艺约束关系建立产品工艺树模型，将工艺树模型中工序的加工顺序取反，形成自顶向下调度的工艺树模型。然后，按短用时策略确定各个工序和加工设备的对应关系。再采用空闲设备驱动策略，建立空闲设备集、可调度工序集、加工工序集和每个设备的备选工序集。驱动时刻，系统按序优先为存在预调度工序的空闲设备确定加工工序：如果当前空闲设备的备选工序集只有一个预调度工序，则直接调度加工；如果有多个预调度工序，则按动态实质短路径策略确定实质短路径上的预调度工序加工。当所有存在预调度工序的空闲设备都处理完毕后，对于其余的不存在预调度工序的空闲设备，则按设备尽量忙原则从可调度工序集剩余的工序中选择工序加工，更新设备集和工序集的状态。该驱动时刻所有空闲设备都调度完毕后，计算下一设备驱动时刻。在下一驱动时刻，更新所有工序集和设备集的状态，并重新按上面描述的调度过程驱动空闲设备调度工序加工。如此不断地循环，直至全部工序都加工完毕。

3 算法设计

算法的具体步骤如下：

1）设置工序属性。pi为工序i的名称；{ti1，…，tiD}为工序pi在D个设备上的加工时间集合；{m1，m2，…，mD}为pi的D个可柔性加工设备集；ci为pi的紧前工序数，每个工序的紧前工序唯一，初始时刻，叶节点工序无紧前工序，设置为0，其余工序的紧前工序设置1；li为pi的路径长度；{ni1，ni2，…，nix}为pi的紧后工序名称，其中x为紧后工序个数，初始时刻，根节点不唯一且无紧后工序，其余工序的紧后工序设置为紧后工序名称。于是，工序属性可以表示为pi / {ti1，ti2，…，tiD} / {m1，m2，…，mD} / ci / li / {ni1，ni2，…，nix}。

2）设置设备m的状态属性。mbusy = 1为设备忙，mbusy = 0为设备空闲。

3）短用时策略确定柔性工序Pi（1≤i≤n）的预加工设备。

4）计算所有工序的路径长度li。

根节点工序不唯一且其紧后工序数为0，因此，所有根节点的路径长度为其各自的加工时间。非根节点工序pi对应的路径长度li可以通过pi的紧后工序Pj（1≤j≤n）的路径长度lj加上该非根节点工序的加工时间ti的最大值得到。

5）空闲设备驱动策略。

6）调度结束。

其中步骤5）空闲设备驱动策略又分为以下7个步骤：

1）建立可调度工序集S。初始时刻T0，只有一个叶节点工序∈ S。非初始时刻，根据工序Pi的紧前工序个数属性ci，将ci = 0的工序动态更新到S中。

2）建立加工工序集H。初始时刻T0，H为空。

3）建立空闲设备集midle。初始时刻T0，所有设备均处于空闲状态，所有设备∈ midle。非初始时刻，根据设备的状态属性，将mbusy = 0的设备动态地添加到midle中。

4）建立设备的备选工序集。初始时刻T0，将每个设备的预调度工序加入该设备的备选工序集。

5）确定Tk时刻空闲设备上的加工工序。首先系统按序为备选工序集中存在预调度工序的空闲设备确定加工工序。即对于某空闲设备，如果它的备选工序集中只有一个预调度工序，则直接调度加工；如果存在多个预调度工序，则按动态实质短路径策略确定预调度工序加工。

另外，此时刻还有设备空闲且S不为空，遵循设备尽量忙原则，系统按序为这些空闲设备从可调度工序集选择工序加工。

6）更新设备集和工序集的状态。将该时刻确定的所有加工工序Pi（1≤i≤n）加入加工工序集H，并将Pi（1≤i≤n）从S和设备的备选工序集中删除。将加工设备的mbusy信号置1，并分别计算加工结束时间T = Tk + ti（Tk为当前驱动时刻，ti为Pi的加工时间）。

7）在下一设备驱动时刻的更新操作。将H中的加工结束时间最小值Tk+1 = min{Tk + ti}确定为下一驱动时刻。在Tk+1时刻，将加工完毕的设备的mbusy信号置0，将加工结束的工序Pi（1≤i≤n）从H中删除，对于每一个加工结束的工序Pi，将Pi的所有紧后工序Pj（1≤j≤n - 1）的紧前工序数属性cj置0，将Pj加入可调度工序集S。判断S是否为空，如是，转步骤6），否则转步骤5）。

4 实例对比与分析

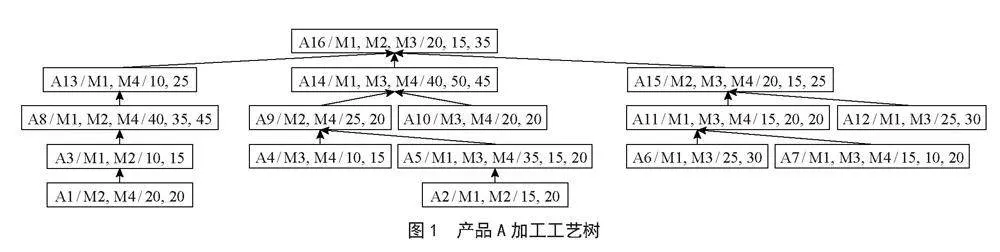
设复杂单产品A有16个工序，在4台设备上加工，图1为A的加工工艺树。下面分别用文献[7]的算法和本文提出的算法对产品A进行调度。

4.1 算法1：文献[7]中的短用时策略

首先按短用时策略对柔性产品进行化简，缩小工序加工设备的选择范围，使其转化为在单一设备上加工的调度问题。接着，按拟关键路径法确定工序的调度次序。在整个调度过程中遵循工序尽早加工的要求确定各工序的开始时间，加工甘特图如图2所示。

4.2 基于设备驱动和实质路径的逆序柔性综合调度算法

首先将图1中可柔性加工工序的加工次序约束关系取反，构造逆序产品工艺树。再采用短用时策略确定各柔性工序的预加工设备，缩小工序加工设备的选择范围。

初始时刻T0 = 0，建立空闲设备集M为{M1，M2，M3，M4}；建立设备的备选工序集O为{M1{}，M2{A16}，M3{}，M4{}}；建立可调度工序集S为{A16}。此时，只有M2的备选工序集中有预调度工序A16，直接调度加工，更新设备集和工序集，计算加工结束时间T1 = 15作为下一驱动时刻。

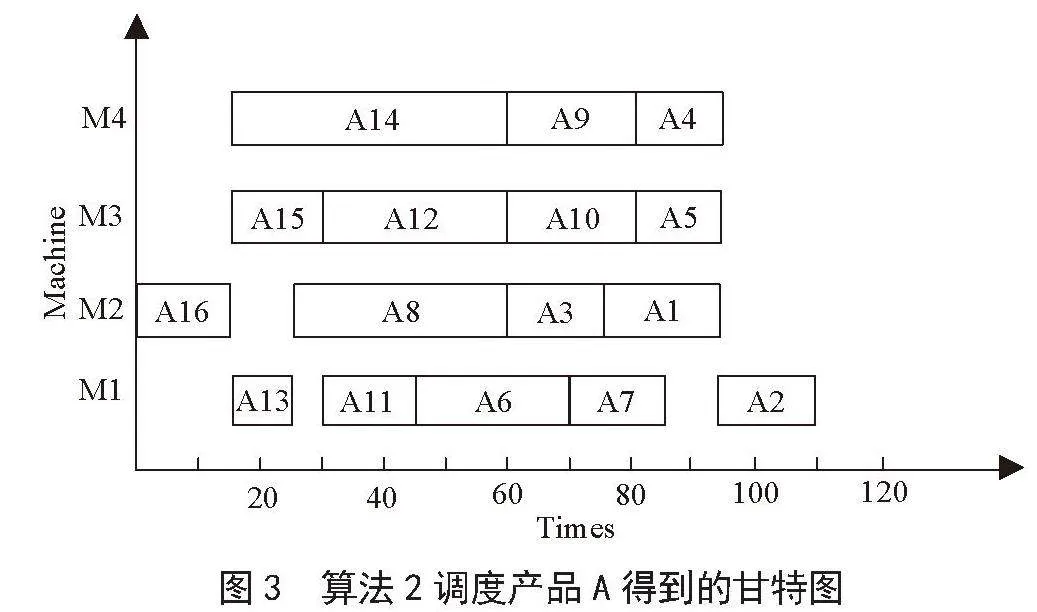
在T1 = 15时刻，A16调度完毕，其后继工序A13，A14，A15成为可调度工序，此时空闲设备集为{M1，M2，M3，M4}，备选工序集为{M1{A13，A14}，M2{}，M3{A15}，M4{}}，可调度工序集S为{A13，A14，A15}。M1上预调度工序不唯一，采用动态实质短路径策略，确定实质短路径上的工序A13在M1上加工。M3上有且仅有一个预调度工序A15。M2和M4无预调度工序，但此时可调度工序集S不为空，依次为M2和M4搜索S中是否有可加工工序，此时S中只有一个工序A14，其可在M4上加工，因此调度A14到M4上加工。M2上无可调度工序，继续处于空闲状态。将此时刻确定的所有加工工序加入加工工序集H，将它们从S和O中删除，并分别计算加工结束时间。选择H中的最早加工结束时间作为下一驱动时刻。在下一驱动时刻按以上过程重新对产品进行调度，如此循环，直至全部工序调度完毕。采用本文算法的调度甘特图如图3所示。

通过对比甘特图可以看出，本文提出的算法2明显地优于算法1，工序间充分地实现了并行处理，在产品制造时间和设备利用率上都得到了显著的提升。

5 结 论

本文提出算法的主要优点：1）为使当前工序加工完毕后，其后继工序可以立即调度加工，采用逆序方式对产品工艺树进行调度。2）为动态确定并行工序、方便操作和提高设备利用率，采用设备驱动策略。3）为使每个工序尽可能在加工用时最短的设备上加工，在驱动时刻，优先处理存在预调度工序的空闲设备。4）为解决大量工序排队等待加工时如何确定调度工序，采用实质短路径策略。5）为避免空闲设备闲置，使设备利用率最大化，采用备尽量忙原则。因此，提出算法可以提高柔性综合设备利用率，增加工序间的并行处理，缩短产品完工时间，对柔性综合调度的深入研究有重要的借鉴作用。

参考文献：

[1] SCHWORM P，WU X Q，GLATT M，et al.Solving Flexible Job Shop Scheduling Problems in Manufacturing with Quantum Annealing [J].Production Engineering，2022，17（1）：105-115.

[2] 胡瑞淇，程辉，张执南.基于表达式树的顺序柔性车间调度问题求解 [J/OL].计算机集成制造系统，2022：1-15[2024-07-04].http：//kns.cnki.net/kcms/detail/11.5946.tp.20220317.1506.002.html.

[3] TUTUMLU B，SARAC T. A MIP Model and a Hybrid Genetic Algorithm for Flexible Job-Shop Scheduling Problem with Job-Splitting [J/OL].Computers & Operations Research，2023，155：106222（2023-03-24）.https：//doi.org/10.1016/j.cor.2023.106222.

[4] ZHU K K，GONG G L，PENG N T. Dynamic Distributed Flexible Job-Shop Scheduling Problem Considering Operation Inspection [J/OL].Expert Systems with ApplicatiRNcr9PZkb+LyQm9wV+jjDYyXEykgeDzoxl/Ddu/g7Ws=on，2023，224：119840（2023-03-01）.https：//api.semanticscholar.org/CorpusID：257488716.

[5] 巴智勇，袁逸萍，李明，等. 考虑分层耦合约束的复杂产品综合调度算法 [J]. 计算机集成制造系统，2023：1-24.

[6] 曹望成，谢志强，裴莉榕.考虑工序序列动态时间紧迫度的逆序贪婪综合调度算法 [J].电子与信息学报，2022，44（5）：1572-1580.

[7] XIE Z Q，HAO S Z，YE G J，et al. A New Algorithm For Complex Product Flexible Scheduling with Constraint Between Jobs [J].Computers & Industrial Engineering，2009，57（3）：766-772.

[8] 谢志强，吕妮.存在预启动设备的综合调度算法 [J].机械工程学报，2021，57（17）：217-225.

[9] 谢志强，桂忠艳，杨静.基于设备驱动和实质路径的动态并行综合柔性调度算法 [J].机械工程学报，2014，50（18）：203-212.

[10] 桂忠艳，杨静，谢志强.基于剪枝分层的柔性加工车间调度算法 [J].控制与决策，2017，32（11）：1921-1932.

[11] 杨丹.存在多重柔性制造的综合调度研究 [D].哈尔滨：哈尔滨理工大学，2023：35-37.

作者简介：桂忠艳（1987—），女，汉族，黑龙江哈尔滨人，工程师，博士研究生，研究方向：调度算法优化、数据挖掘。