Python在应用统计学课程教学中的应用

摘 要：应用统计学是高等院校绝大多数经管类专业的专业基础课程，对学生统计思想的培养和后续专业课程的学习起着承上启下的重要作用。文章旨在探讨将Python编程技术引入应用统计学课程的教学改革，以抽样分布（卡方分布、t分布和F分布）为例，深入研究其在统计学课程中的实际应用。通过分析Python在教学中的基础应用、抽样分布的应用实践，以及Python编程技术在教学中的积极影响发现，Python应用能使学生更好地理解抽样分布的概念、原理，可为高等院校的统计类课程培养数字时代所需人才的改革提供一些参考。

关键词：抽样分布；卡方分布；t分布；F分布；Python

中图分类号：TP39；G434 文献标识码：A 文章编号：2096-4706（2024）14-0183-07

Application of Python in the Teaching of Applied Statistics Course

GUO Peng

（Xi'an Technology and Business College， Xi'an 710200， China）

Abstract： Applied Statistics is a fundamental course for the majority of economics and management majors in higher education institutions， playing an important role in cultivating students' statistical thinking and studying of subsequent professional courses. This paper aims to explore the teaching reform of introducing Python programming technology into the course of Applied Statistics， using sampling distributions （Chi-square distribution， t distribution， and F distribution） as examples to deeply study their practical applications in statistics courses. By analyzing the basic application of Python in teaching， the practical application of sampling distribution， and the positive impact of Python programming technology in teaching， it is found that Python application can help students better understand the concept and principle of sampling distribution， and provide some reference for the reform of statistical courses in higher education institutions to cultivate talents needed in the digital era.

Keywords： sampling distribution; Chi-square distribution; t distribution; F distribution; Python

0 引 言

随着计算机技术的迅猛发展，编程语言在统计教学中的应用日益普及。在当今数字化时代，培养学生的数据思维和解决实际问题的能力显得尤为关键。Python作为一门易学易用的编程语言，在数据科学和统计学领域广受欢迎。本文以Python编程技术为基础，深入研究其在应用统计学教学中的探索与实践，特别关注抽样分布的教学应用，包括卡方分布、t分布和F分布[1]。

通过构建实际问题场景，本文展示了Python技术在统计学教学中的技术优势。充分利用Python强大的功能，有助于学生更好地理解抽样分布这一抽象而难以理解的概念，进而提升他们在统计推断、数据分析和编程方面的能力。将Python作为计算模型学习的工具赋能统计课程教学与实践[2]，这一教学方法积极地影响了学生的学习效果，使他们能够更自信、灵活地应对复杂且抽象的统计学问题。同时通过可视化编程技术将统计理论进行图形图像数字化表达，这样的学习体验不仅有助于拓展学生的认知视野，还为他们在未来的学术和职业领域的研究与工作奠定坚实的基础。

1 Python在统计教学中的基础应用

1.1 数据可视化与探索性数据分析

1.1.1 Matplotlib和Seaborn的介绍

作为Python中的绘图库，Matplotlib提供了丰富的绘图工具，能够创建各种类型的图表，如折线图、散点图等。

Seaborn是建立在Matplotlib之上的高级绘图库，简化了绘图的流程，并提供了更美观的默认主题。

1.1.2 绘制直方图、箱线图等图形

使用Matplotlib和Seaborn绘制直方图，可以直观展示数据的分布情况，有助于学生理解数据的形态。

利用箱线图，学生能够更清晰地识别数据的分散程度和异常值。

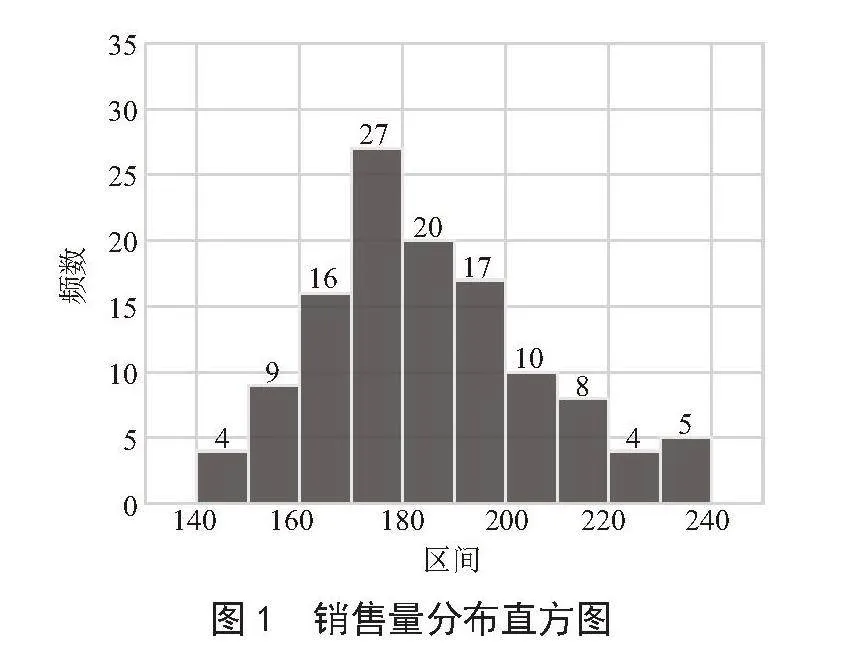
从图1可以更好地了解销售量的分布情况，发现销售量在不同范围内的分布，以此帮助确定销售量在哪些区间内较为活跃或较为稳定，比如峰值附近的区域表示销售量较为集中的范围，对称分布可能表示销售量在中心趋势附近均匀分布，而偏斜分布可能表示销售量在某一方向上更为集中等。

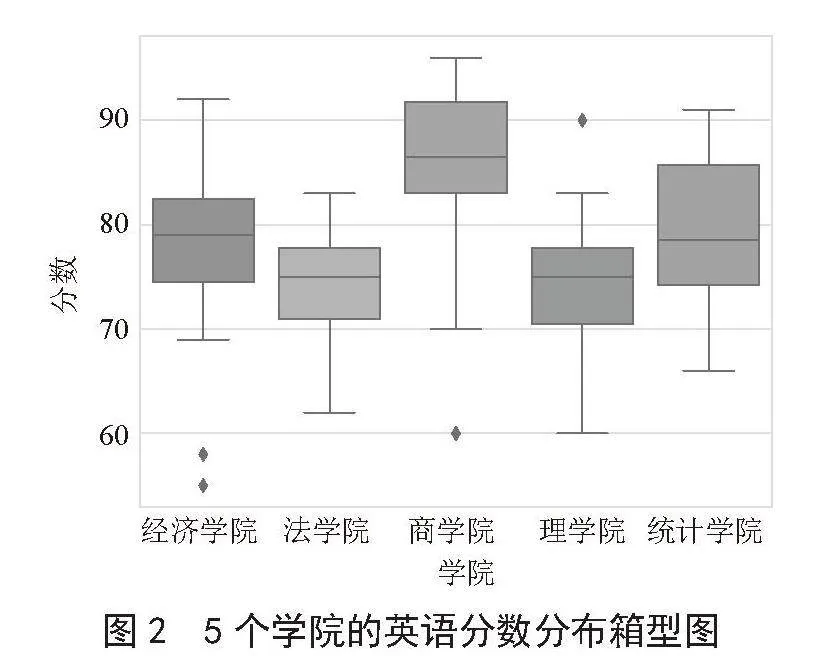
从图2可以看到箱型图提供了有关数据集中趋势、离散程度和异常值的信息。通过观察5个学院的英语分数分布箱型图，可以获取到各学院英语成绩的中位数、分布离散程度、上下四分位数、箱型图的对称性以及异常值等重要信息。

1.2 认识抽样分布

1.2.1 卡方分布

卡方分布（x2分布）是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布[3]。

卡方分布常用于假设检验和置信区间的计算。

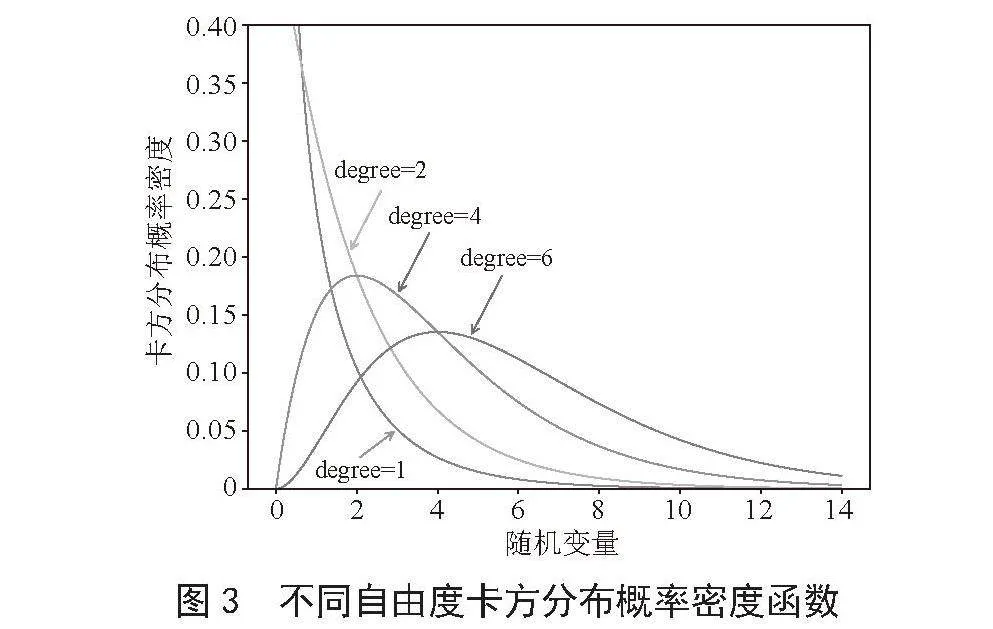
如图3所示，经过程序实现卡方分布图形可以看出，每一个自由度决定了一条曲线形状，当自由度为1、2时显示为指数曲线，当自由度＞2时，显示为单峰曲线，随着自由度逐步变大，曲线峰逐步向右移动，当n趋向于无穷大时，则卡方分布曲线趋近于正态分布[4]。

卡方分布曲线模拟程序如下：

# 生成模拟数据

x = np.arange（0.， 14.， 0.01）

# 自由度（degree=1）的卡方分布随机数概率密度函数

y = st.chi2.pdf（x， 1）

# annotate函数设置指向概率密度函数曲线的箭头和文字

plt.figure（figsize=（8， 6））

plt.annotate（"degree=1"， xy=（3， st.chi2.pdf（3， 1）），

xytext=（0.7， st.chi2.pdf（3， 1） - 0.04）， weight="bold"，

color='steelblue'， fontsize=14，

arrowprops=dict（arrowstyle="->"， connectionstyle="arc3"， color="steelblue"））

y1 = st.chi2.pdf（x， 2）

y2 = st.chi2.pdf（x， 4）

y3 = st.chi2.pdf（x， 6）

plt.plot（x， y）

plt.plot（x， y1）

plt.plot（x， y2）

plt.plot（x， y3）

plt.title（"卡方分布概率密度函数"， size=14）

plt.xlabel（"随机变量"， size=14）

plt.ylabel（"卡方分布概率密度"， size=14）

plt.ylim（0.， 0.4）

plt.show（）

1.2.2 t分布

在概率论和统计学中，t分布（t-distribution）用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知或者在样本数量足够多时，则应该用正态分布来估计总体均值。

t分布曲线形态与n（自由度df）大小有关。与标准正态分布曲线相比，自由度df越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线，当自由度df = ∞时，t分布曲线为标准正态分布曲线。

t分布特征为：

1）t分布为一簇曲线，以0为中心，左右对称。

2）t分布形态与df有关；df越小，t峰越低尾越高。

3）df无穷大时，t分布趋近于标准正态分布N（0，1）。

4）自由度不同，则t分布曲线不同，曲线下95%面积的界值随着自由度变化，具体可以查t界值表。

t分布的用途主要为对总体均值的估计和假设检验（t检验）。

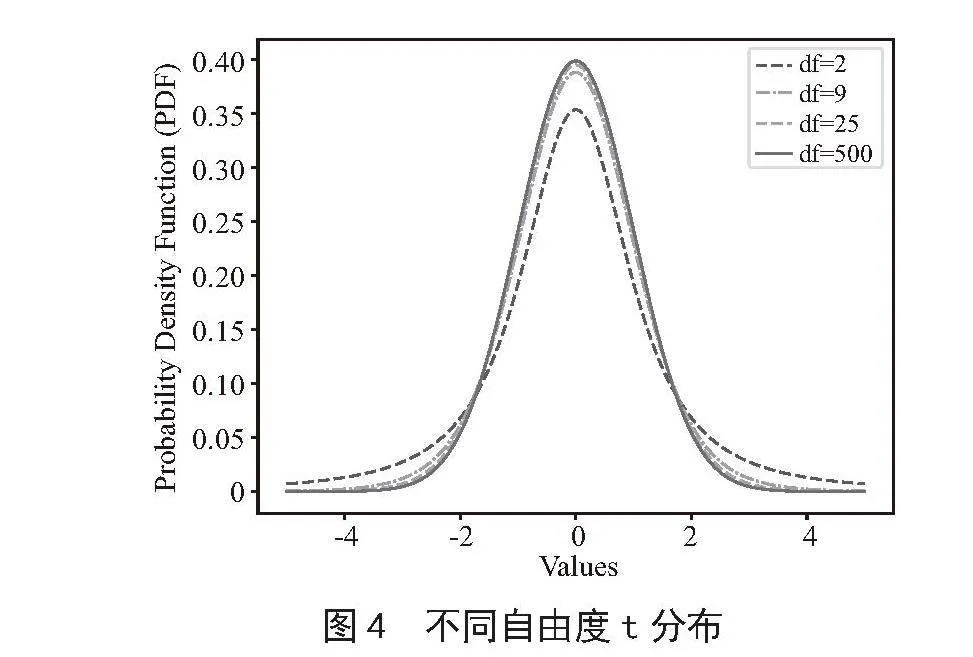
从图4可以看出，不同的自由度会影响t分布的形状。随着自由度的增加，t分布的形状会越来越接近正态分布。

当自由度较小时（例如1或2），t分布的形状会比较扁平，尾部较厚，这意味着在小样本情况下，观测值偏离均值的可能性较大。

当自由度较大时（例如30或更大），t分布的形状会接近正态分布，此时t检验的结果会更稳定。

t分布曲线模拟程序如下：

# 自由度

degrees_of_freedom = [2， 9， 25， 500]

# 生成 x 轴数据

x = np.linspace（-5， 5， 1000）

# 绘制 t 分布曲线

for i， df in enumerate（degrees_of_freedom）：

if df == 500：

plt.plot（x， t.pdf（x， df）， label=f'df = {df}'，

linestyle='solid'）

else：

linestyle = '--' if i % 2 == 0 else '-.' # 切换虚线样式

plt.plot（x， t.pdf（x， df）， label=f'df = {df}'，

linestyle=linestyle）

# 添加标题和标签

plt.title（'t Distribution with Different Degrees of Freedom'）

plt.xlabel（'Values'）

plt.ylabel（'Probability Density Function （PDF）'）

# 添加图例

plt.legend（）

# 显示图形

plt.show（）

1.2.3 F分布

F分布是1924年英国统计学家Ronald.A.Fisher爵士提出，并以其姓氏的第一个字母命名的。它是两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布，是一种非对称的右偏抽样分布，由两个自由度决定分布形状，当两个自由度越来越大时，F分布形状趋近于正态分布。

F分布有着广泛的应用，如在双样本方差F检验、回归方程的显著性检验中都有着重要的地位。

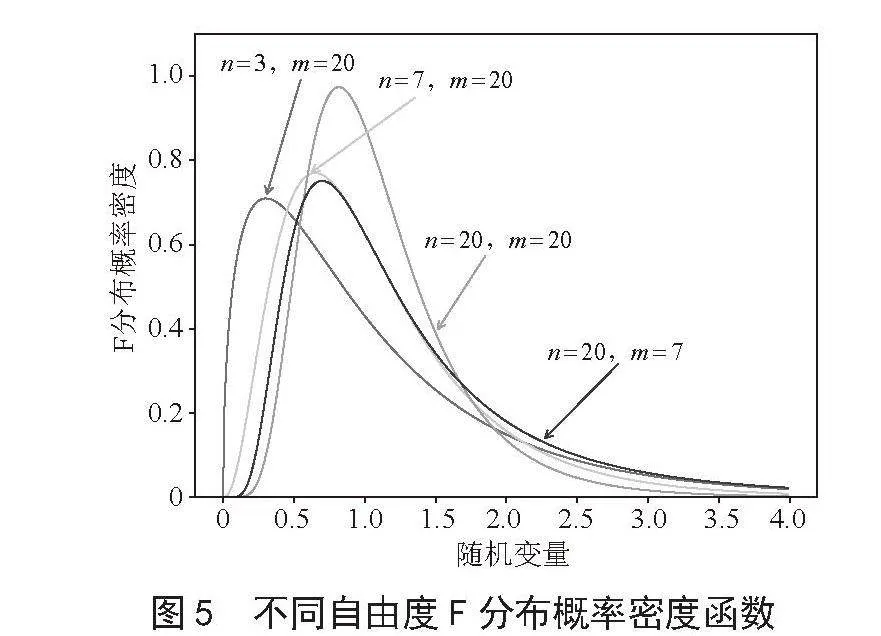
从图5中可以看出当n和m较小时，F分布曲线呈现偏态分布，且随着自由度的增加，F分布曲线逐渐接近正态分布的形状。通过比较不同自由度的F分布曲线，可以了解在不同自由度下F统计量的概率分布情况，从而更准确地判断两个总体方差是否存在显著差异。

F分布曲线模拟程序如下：

plt.figure（figsize=（8， 6））

# 生成模拟数据

x = np.arange（0.， 4.， 0.01） # 随机数

y = st.f.pdf（x， 3， 20） # 自由度为（3，20）的F分布随机数概率密度函数

# annotate函数设置指向概率密度函数曲线的箭头和文字

plt.annotate（"n=3，m=20"， xy=（0.3， st.f.pdf（0.3， 3， 20）），

xytext=（0.3， st.f.pdf（.3， 3， 20） + 0.3）， weight="bold"， color='steelblue'，

fontsize=14，arrowprops=dict（arrowstyle="->"， connectionstyle="arc3"，

color="steelblue"））

y1 = st.f.pdf（x， 7， 20）

y2 = st.f.pdf（x， 20， 20）

y3 = st.f.pdf（x， 20， 7）

plt.plot（x， y）

plt.plot（x， y1）

plt.plot（x， y2）

plt.plot（x， y3）

plt.title（"F分布概率密度函数"， size=14）

plt.xlabel（"随机变量"， size=14）

plt.ylabel（"F分布概率密度"， size=14）

plt.ylim（0.， 1.1）

plt.show（）

通过绘制这些分布的图形，可以直观地观察和分析数据的分布特征，更好地理解这些分布的特点。同时，可以通过比较模拟数据和理论分布，验证模拟方法是否准确。在实际应用中，如假设检验、置信区间估计等统计推断方法都需要用到这些分布。通过模拟生成这些分布的数据，可以更好地理解这些方法的工作原理，并在实际项目中进行应用。

2 抽样分布教学实践

在概率论和数理统计案例教学中，借助Python科学计算库Scipy可以实现各类应用的统计分析功能，如假设检验、拟合分布、计算置信区间等，帮助研究者更好的理解数据的分布、趋势和关系，从而更好地进行实际应用的概率计算、数据分析和模型构建[5]。

2.1 卡方分布在假设检验中的应用

卡方检验是一种非参数统计检验，用于确定预期值和观测值的分布之间是否存在显著差异，用于检测观察到的类别变量的分布是否与期望的不同，分为单因素卡方检验（卡方拟合优度检验）、双因素卡方检验（卡方独立性检验）[6]。

卡方拟合优度检验：依据总体分布状况，计算出分类变量中各类别的期望频数，与分布的观察频数进行对比，判断两者是否有显著性差异，从而对分类变量进行分析[7]。特指一个分类变量的期望频数与观察到的频数相比较是否存在显著差异。其自由度df = k - 1，k表示分类变量类型个数，期望频数=类别比例×观察总数。

卡方独立性检验：检验两个类别变量之间是否存在关系。其自由度df = （R-1）（C-1），期望频数= fr fc / n，其中fc表示列频数和，fr表示行频数和，n表示观察值的总数。

以卡方拟合优度检验为例，其实现步骤如下：

1）建立假设：

零假设（H0）。两个分类变量之间没有显著差异，即相互独立。

备择假设（H1）。两个分类变量之间存在显著差异，即相互依赖。

2）计算期望频数。根据研究的问题和样本数据的特点，计算期望频数。期望频数通过总样本量乘以每个类别在总样本中的比例得到，即为期望频数=类别比例×观测总数。

3）计算观察频数。统计每个类别的观察频数，即实际观测到的频数。

4）设置显著性水平。确定显著性水平（通常为0.05或其他预先选择的值），以便在假设检验中进行比较。

5）计算卡方统计量。使用以下卡方统计量的公式计算观察频数与期望频数之间的差异。

其中，Qi表示观察频数，Ei表示期望频数，总和是针对所有类别的。

6）确定自由度。确定自由度的数量，通常为类别数目减去1，计算自由度df = k - 1，其中k表示类别数目。

7）查找临界值或计算p值。使用卡方分布表或计算p值来比较计算得到的卡方统计量与临界值。如果p值小于显著性水平，拒绝零假设。

8）做出决策。如果p值小于显著性水平，拒绝零假设，认为观察频数与期望频数存在显著差异；否则，接受零假设。

2.1.1 实例分析

场景描述：1912年4月15日，一艘乘坐891名乘客的泰坦尼克号与冰山相撞后沉没。轮船乘客信息包括PassengerId（乘客编号）、Survived（0 =丧生，1 =生还）、Pclass（客舱等级1、2、3）、Name（姓名）、Sex（性别）等信息，如表1所示。

检验目的：卡方检验是一种用于比较观察到的频率和期望频率之间差异的统计学方法。在实例研究中，利用卡方拟合优度检验比较乘客客舱等级对乘客生存（Survived）情况是否有影响[8]。

2.1.2 Python代码实现

依据卡方拟合优度检验实现步骤，通过Python代码编程实现如下：

#导入数据集

data = pd.read_csv（r"train.csv"， index_col='PassengerId'，

usecols=['PassengerId'， 'Pclass'， 'Survived']）

#计算观察频数

PClass_survd = pd.pivot_table（data， index=['Pclass']，

columns=['Survived']， aggfunc='size'）

# 每个客舱等级按行求和，计算每个客舱等级人数占总人数的比例。

pct_class = PClass_survd.sum（axis=1） / 891

# 每个生还情况按列求和，计算生与死人数占总人数的比例。

pct_survived = PClass_survd.sum（axis=0） / 891

#计算期望频数

exp = round（pct_class.to_frame（） @ （pct_survived.to_frame（）.T） * 891）

# 计算卡方值

Chi_table = （（PClass_survd - exp） ** 2） / exp

#求所有客舱等级每个生还与死亡乘客的卡方值总和

Chi_value = Chi_table.sum（）.sum（）

df=3-1=2# 自由度等于分类变量类型个数-1

p_value = chi2.sf（Chi_value， df）

#计算卡方值与p值

print（"Chi square value is "， Chi_value）

print（"P value is"， p_value）

# Chi square value is 101.87213414657131

# P value is 7.563923715789563e-23

#根据P值，P值远小于显著性水平0.05，则拒绝零假设。

#结论：乘客客舱等级与乘客生还情况之间存在显著差异，即相互依赖。

2.1.3 数据分析结论

经过数据分析，根据卡方拟合优度检验，得出结论为舱位等级对幸存者的生存机会具有重要影响。船舱越靠上的乘客幸存率越高，这是因为这些乘客更容易得到救援和生存条件。

基于以上分析，我们可以举一反三，通过卡方检验分析性别、年龄、国籍等不同因素对乘客生存情况的影响程度。

2.2 t分布在假设检验中的应用

t检验，亦称student t检验，主要用于样本含量较小（n＜30），总体标准差σ未知的正态分布。它是用t分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。t检验分为单总体检验、双总体检验和配对样本检验。

以单总体检验t检验为例：

单总体检验：比较一个样本均值所代表的未知总体均值u和已知总体均值μ0是否存在显著差异。

其实现步骤如下：

1）建立假设：

零假设（H0）。样本均值等于理论上的总体均值μ0。

备择假设（H1）。样本均值不等于理论上的总体均值μ0。

2）选择显著性水平。选择适当的显著性水平（通常为0.05），表示在统计上认为差异是显著的。

3）计算样本统计量。计算样本均值（）和样本标准差（s）

4）计算t统计量。使用以下公式计算t统计量：

其中，μ0表示理论上的总体均值，n表示样本容量。

5）确定自由度。自由度为n - 1，其中n为样本容量。

6）查找p值。使用t分布表或统计软件计算t统计量对应的p值。

7）查找p值。使用t分布表或统计软件计算t统计量对应的p值。

8）做出决策。比较p值与选择的显著性水平。如果p值小于显著性水平，拒绝零假设，认为样本均值与理论上的总体均值存在显著差异。

2.2.1 实例分析

场景描述：一家食品加工公司质量控制团队，负责监测一种产品的净重是否符合标准。从生产线上随机选取了一组产品，测量了它们的净重，通过单总体t检验来判断产品的平均净重是否等于标准净重。

检验目的：验证产品的平均净重是否符合标准净重。

2.2.2 Python代码实现

# 设定抽取的净重数据

net_weights = np.array（[150.2， 151.5， 149.8， 150.0， 150.3， 150.1， 150.4， 149.9， 150.2， 150.6]）

# 设定标准净重

standard_weight = 150.0

# 执行单总体t检验

t_statistic， p_value = ttest_1samp（net_weights， standard_weight）

# 显示t统计量和p值

print（f"t统计量： {t_statistic}"）

print（f"p值： {p_value}"）

# 判断显著性水平为0.05

alpha = 0.05

if p_value< alpha：

print（"拒绝零假设，说明产品的平均净重与标准净重存在显著差异。"）

else：

print（"无法拒绝零假设，没有足够证据表明产品的平均净重与标准净重存在显著差异。"）

2.2.3 数据分析结论

程序运行结果如下：

t统计量：1.963 961 012 124 011 2

p值：0.081 126 188 845 830 13

根据实际计算得到的t统计量与临界值或p值的比较，得出结论：p＞0.05，故无法拒绝零假设，没有足够证据表明产品的平均净重与标准净重存在显著差异。

2.3 F分布在假设检验中的应用

双样本方差F检验是一种统计方法，用于检验两个正态总体方差是否存在显著差异[9]。

以双样本方差F检验为例，其实现步骤如下：

1）建立假设：

零假设（H0）。两个总体的方差相等 。

备择假设（H1）。两个总体的方差不相等 。

2）选择显著性水平。选择适当的显著性水平（通常为0.05），表示在统计上认为差异是显著的。

3）计算F统计量。使用以下公式计算F统计量：

4）查找临界值。在F分布表中查找临界值，根据自由度df1与df2，以及选择的显著性水平。

5）查找临界值。如果计算得到的F统计量大于临界值，则拒绝零假设，认为两个总体的方差不相等。

如果计算得到的F统计量小于等于临界值，则不拒绝零假设，认为两个总体的方差相等。

2.3.1 实例分析

场景描述：两工厂生产同一份零件且零件尺寸服从正态分布，A生产的16个零件中，均值为3.1，样本方差为0.04；B生产的25个零件中，均值为3.08，样本方差为0.09。

检验目的：能否在0.05的显著性水平下认为两工厂生产零件的误差（方差）相同？

2.3.2 Python代码实现

# 样本A

Mean_A = 3.1

Variance_A = 0.04

n_A = 16

# 样本B

Mean_B = 3.08

variance_B = 0.09

n_B = 25

# 计算F统计量

F_statistic = variance_A / variance_B

# 计算自由度

df1 = n_A - 1

df2 = n_B - 1

# 查找临界值，这里使用分位数函数 ppf

alpha = 0.05

critical_value = stats.f.ppf（1 - alpha / 2， df1， df2）

# 判断是否拒绝零假设

reject_null = abs（F_statistic） >critical_value

print（f"F统计量： {F_statistic}"）

print（f"临界值： {critical_value}"）

print（"拒绝零假设" if reject_null else "接受零假设"）

2.3.3 数据分析结论

程序运行结果如下：

F统计量：0.444 444 444 444 444 5

临界值：2.437 429 109 077 491 8

根据实际计算得到的F统计量与临界值比较，得出结论：F统计量＜临界值，故接受零假设，没有充分理由拒绝原假设，因此可以判断两工厂生产零件误差大致相同。

3 教学应用中的问题与改进建议

在教学过程中对于没有编程基础或基础薄弱的学生来说，这种多学科交叉授课模式，学生会感到非常困惑，学习曲线也较陡峭。学生存在无法理解或掌握足够的知识来处理复杂的数据统计分析和推断任务，特别是在处理复杂统计模型时，需要一定的编程技巧。另外，在教学中，存在理论学习和实践操作脱节的问题，如何将统计学的理论知识转化为Python的实际操作，需要教师精心的教学设计。

对此考虑以下教学建议：

1）循序渐进地教学：根据学生的基础，在统计学章节知识点教学中从易到难逐步推进和引入更复杂的统计模型和方法。同时，通过大量实例和案例来帮助学生理解和应用。

2）学习不止于课堂，教师可以提供详细的技术指南，帮助学生解决学习过程中问题。此外，可以利用在线交流的形式，为学生提供实时的技术支持。

3）通过项目或实验的形式，让学生将所学的理论知识应用到实际的数据分析中。这不仅可以帮助学生巩固知识，还可以提高他们的实践能力和问题解决能力。

4）Python有很多强大的数据可视化库，如Matplotlib、Seaborn等。教师可以引导学生利用这些工具进行数据可视化，帮助学生更直观地理解数据和分析结果。

最后，鼓励学生分组合作，共同解决数据分析问题。培养学生的团队协作能力，在交流和讨论中互相学习、共同进步[10]。

4 结 论

Python编程技术与统计学课程的交叉融合旨在培养学生运用信息技术手段，通过对抽样分布曲线和实际问题场景的模拟仿真与案例实践，激发学生对应用统计学的学习兴趣。这一整合的教学方法不仅促进了对统计学抽象理论的深刻理解，还使课程内容更为生动有趣，激发了学生的学习热情，有助于提升学生的动手实践能力和问题解决能力，使其更好地适应数字时代人才发展的需求，为其未来职业发展奠定坚实的基础。

参考文献：

[1] 张华初，楚鹏飞，谢观霞.统计分布和中心极限定理的随机模拟 [J].统计与决策，2021，37（4）：69-72.

[2] 刘衍，王刚，杨兴春，等.公安院校基于python语言的程序设计网络课程教学探索 [J].四川警察学院学报，2019，31（4）：106-110.

[3] 徐鹏.偏正态分布与偏t分布的研究 [D].南京：南京邮电大学，2023.

[4] 王宁，孙晓玲.智能手机端Python语言的数学实验案例设计 [J].合肥师范学院学报，2019，37（6）：117-121.

[5] 贺玲，肖蕾，罗刚，等.案例驱动教学法在Python教学中的应用 [J].微型电脑应用，2021，37（1）：134-136.

[6] 房祥忠.卡方分布与卡方检验 [J].中国统计，2022（5）：29-31.

[7] 袁欧，何山.基于python的Z检验法和T检验法研究 [J].大众标准化，2022（15）：174-176.

[8] 周步祥，黄河，刘治凡，等.基于假设检验的快速事件检测算法 [J].合肥师范学院学报：工程科学与技术，2020，52（4）：42-48.

[9] 丁建华，李俊.F分布的Excel构建与模拟 [J].韶关学院学报，2019，40（12）：9-12.

[10] 叶小青.Python在《概率论与数理统计》教学中的应用 [J].中外企业家，2020（8）：226-227.

作者简介：郭鹏（1980.05—），男，汉族，陕西西安人，助教，软件工程硕士，研究方向：数据挖掘、金融大数据分析。

收稿日期：2023-12-22

基金项目：西安工商学院教育教学改革项目（22YJ14）

DOI：10.19850/j.cnki.2096-4706.2024.14.037