基于可靠度理论的岩质滑坡稳定性及敏感性分析

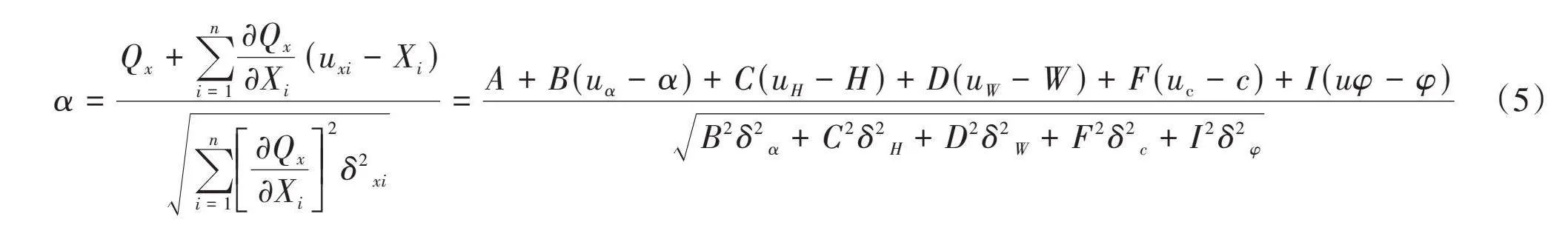
摘 要：【目的】研究西藏高海拔地区岩质滑坡的主要失稳机理。【方法】以数学方程中可靠度理论为基础，根据岩质滑坡圆弧滑动稳定性极限特征，结合现场大量试验及数学概率统计，建立其可靠度判定极限状态方程。【结果】研究结果表明：公式中坡度[α]、坡高H、单位长度滑体的重力W、岩石的黏聚力[c]、岩石的内摩擦角[φ]等物理力学参数的均值与变异性系数、可靠度指标存在一定影响规律，并以此建立了岩质滑坡可靠度分析计算模型。【结论】通过各物理力学参数的可靠度敏感性计算分析可知，岩质滑坡的坡度敏感性最高，其次是滑坡的单位长度重力、内摩擦角和黏聚力指标；对于滑坡坡高没有表现出明显的影响规律。

关键词：西藏地区；岩质滑坡；可靠度指标；概率统计；敏感性

中图分类号：TV697.23 文献标志码：A 文章编号：1003-5168（2024）15-0037-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.15.008

Stability and Sensitivity Analysis of Rock Landslides Based on

Reliability Theory

—Taking the Landslide Along the Penduo Water Conservancy Hub in Tibet as an Example

YANG Zhixiang1 ZHAO Hankuo2 HUANG Runqiu3 PEI Xiangjun3

（1.Henan Industrial Design & Research Institute Group Co.， Ltd.， Zhengzhou 451450， China;

2.China Water Northeast Survey， Design and Research Co.， Ltd.， Changchun 130021， China; 3.Chengdu University of Technology State Key Laboratory of Geological Disaster Prevention and Geological Environmental Protection， Chengdu 610059， China）

Abstract： [Purposes] This papers aims to study the main instability mechanisms of rock landslides in high-altitude areas of Tibet. [Methods] Based on the reliability theory in the mathematical equation， according to the limit characteristics of the circular sliding stability of the rock landslide， and combined with a large number of field tests and mathematical probability statistics， the reliability determination limit state equation is established. [Findings] The research results indicate there is a certain influence law between the variability coefficient as well as reliability indicators and mean value of physical and mechanical parameters such as slope [α]， slope height H， gravity per unit length of sliding mass W， rock cohesion C， and internal friction angle [φ] in the formula have certain influence rules. Based on this， a reliability analysis and calculation model for rock landslides was established. [Conclusions] By calculating the reliability sensitivity of various physical and mechanical parameters， it can be concluded that the inclination angle sensitivity of rock landslides is the highest， followed by the unit length weight， internal friction angle， and cohesion index of landslides; there is no obvious impact pattern on the height of the landslide slope.

Keywords： Tibet region; rock landslide; reliability indicators; probability statistics; sensitivity

0 引言

西藏深切峡谷地区，由于河流的下切作用，经常会出现大型滑坡失稳现象，加之在抽水蓄能电站的建设和运营过程中水位上升和下降比较频繁，导致滑坡灾害频发。许多学者对岩质滑坡的稳定性和敏感性进行了研究，但目前通过可靠度理论研究地质灾害还处于初期阶段。张硕等［1］利用可靠度理论对坠落式危岩体稳定性进行了分析。杨智翔等［2］通过可靠度理论对滑移式孤石的稳定性进行了试验分析。以上研究均只考虑变异性指标对计算参数的影响且灾害模型比较单一，无法准确地模拟影响复杂地质灾害的诱发因素，也不能说明预测结果的可靠性，但为本研究进行滑坡地质灾害概率分析提供了方向。因此，通过可靠度理论对岩质滑坡的稳定性和敏感性进行分析对水电站建设和运营具有指导意义。

本研究以滑坡圆弧滑动稳定性极限状态公式为基础，建立可靠度判定滑坡失稳概率方程，并确定可靠度指标的分析方法。根据现场统计试验，对方程中坡度[α]、坡高H、单位长度滑体的重力W、岩石的黏聚力c、岩石的内摩擦角[φ]等基本参数的可靠度指标、变异性和均值的变化规律进行研究，分析各参数对岩质滑坡失稳概率和可靠度指标的敏感性。

1 岩质滑坡稳定性可靠度判定方法

1.1 极限平衡状态分析

本研究根据岩质滑坡圆弧滑动的特点，建立稳定性极限状态方程。引入抗滑力[R（α，H，W，c，φ）]，下滑力[T（α，H，W，c，φ）]两个基本变量，滑坡稳定性极限状态方程见式（1）。

[Q=Q（α，H，W，c，φ）=R（α，H，W，c，φ）-T（α，H，W，c，φ）=0] （1）

代入后公式见式（2）。

[Q=Wcosαtanφ+cHsinαWsinα] （2）

1.2 分布特征及变量分析

根据式（1），运用可靠度理论对滑坡稳定性进行分析，选取[α]、H、W、c、[φ]为变量，进行可靠度参数分析时，公式中的物理力学参数指标分布特征对可靠度计算结果有一定的影响 ［3-5］，在不考虑其他因素影响计算结果的前提下，各变量统计结果见表1。

西藏旁多水利枢纽电站根据现场调查沿线共发育198处大中型滑坡［4-6］。坝址区属高山地形，谷底高程4 027～4 034 m，两岸山顶高程5 300 m左右，比高1 270 m左右。右岸高程4 060 m以下坡度较陡，为50°左右，高程4 060 m以上坡度变缓，为30°左右。右岸山坡大部分基岩裸露，局部被混合土碎（块）石覆盖；左岸高程4 240 m以下被混合土碎（块）石覆盖，坡度较缓，为15°左右，高程4 240 m以上基岩裸露，坡度大于45°。河谷呈不对称U字形。河床靠近右岸，右岸漫滩、阶地发育不完整。左岸漫滩发育，宽约550 m，三级阶地明显，阶地前缘高出河面分别为7 m、14 m和38 m。

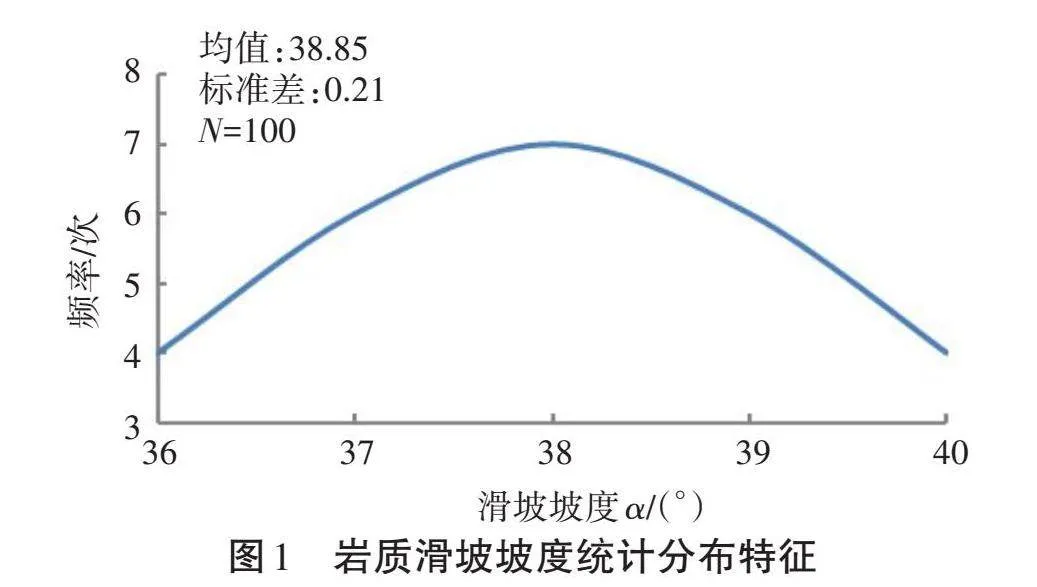
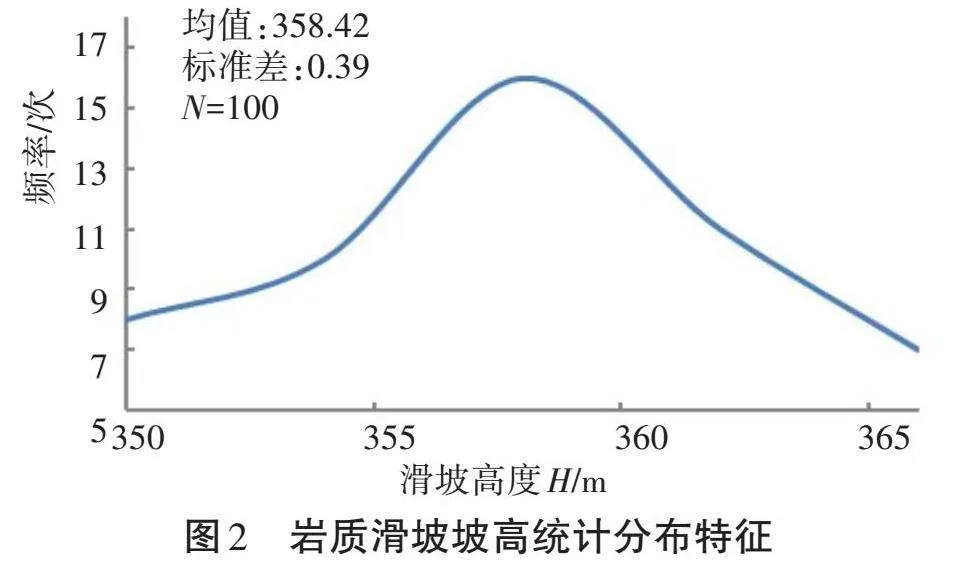
本研究统计分析100处滑坡，得到5个变量的数据，绘制了各变量的分布特征，如图1至图5所示。

1.3 岩质滑坡可靠度指标及失效概率分析方法

令Q=Q（[α，H，W，c，φ]）=Q（X1，X2，X3，X4，X5）=0，则其上一点Qx的均值和标准差分别见式（3）、式（4）。

[E=Qx+i=1n∂Qx∂Xi（uxi-Xi）] （3）

[δ=i=1n∂Qx∂Xi2δ2xi] （4）

以上式中：uxi、δxi分别为影响该点取值的各项变量的平均值和标准差。根据可靠度定义可得式（5）。

式 中：uα、uH、uW、uc、uφ和δα、δH、δW、δc、δφ分别为坡度、坡高、滑体重量、黏聚力和内摩擦角的平均值

和标准差取值。

令[A=Q（uα，uH，uW，uc，uφ）]，[B=∂Q（uα）∂α]，[C=∂Q（uH）∂H]，[D=∂Q（uW）∂W]，[F=∂Q（uc）∂c]，则有式（6）。

[I=∂Q（uφ）∂φ] （6）

当Q=0时，有式（7）、式（8）。

[Zi=（Xi-ui）δxi] （7）

[cosγ=-i=1n∂Qx∂Xiδxii=1n∂Qx∂Xi2δ2xiZi=0] （8）

整理得式（9）。

[Xi=uxi+αcosγiδi] （9）

当[|αi+1-αi|≤]容许误差时，取[α=αi]，失效概率[Pf=1-φ（α）]，[φ（α）]为标准正态分布函数。根据岩质滑坡失稳概率将滑坡分为稳定（Pf<8%）、基本稳定（Pf=8%～35%）、欠稳定（Pf=35%～70%）、稳定性差（Pf=70%～85%）、不稳定（Pf>85%）。通过可靠度判定理论对旁多水利枢纽沿线滑坡进行失稳概率判定，并与其通过稳定性系数计算公式计算的结果进行对比，两者评价结果可相互印证准确性，具体见表2。

2 随机变量与可靠度指标的变化规律

2.1 坡度与可靠度指标敏感性的关系

为了分析岩质滑坡坡度均值和变异系数对稳定性可靠度指标的敏感性，对西藏旁多水利枢纽沿线滑坡坡度分别取坡度均值33°、34°、35°、36°、37°、38°，变异系数为0.022 7、0.023 1、0.023 8、0.024 2、0.024 9、0.031 1，保持其余4种因素不变，分析岩质滑坡稳定性的可靠度指标与均值和变异性系数的变化规律。

根据所采用的坡度均值进行计算，岩质滑坡坡度均值和变异系数可靠度指标计算结果见表3。由表3可知，可靠度指标随着岩质滑坡坡度的增大而减小，几乎为线性变化，递减速率Kα=[3.854−3.74334−33]=0.111，此时最大失效概率增大，因此岩质滑坡坡度增大会导致滑坡失稳可能性变大，这与实际情况相吻合。

由此可知，当滑坡坡度均值增大时，可靠度指标减小；当变异系数增大时，可靠度指标虽然也会减小，但幅度相对较小，而此时最大失效概率增大，递增速率K=[2.058−2.0560.023 1−0.022 7]=0.5。通过比较得出，滑坡坡度变异性系数对岩质滑坡失稳的可靠度敏感性较大。

2.2 坡高与可靠度指标敏感性的关系

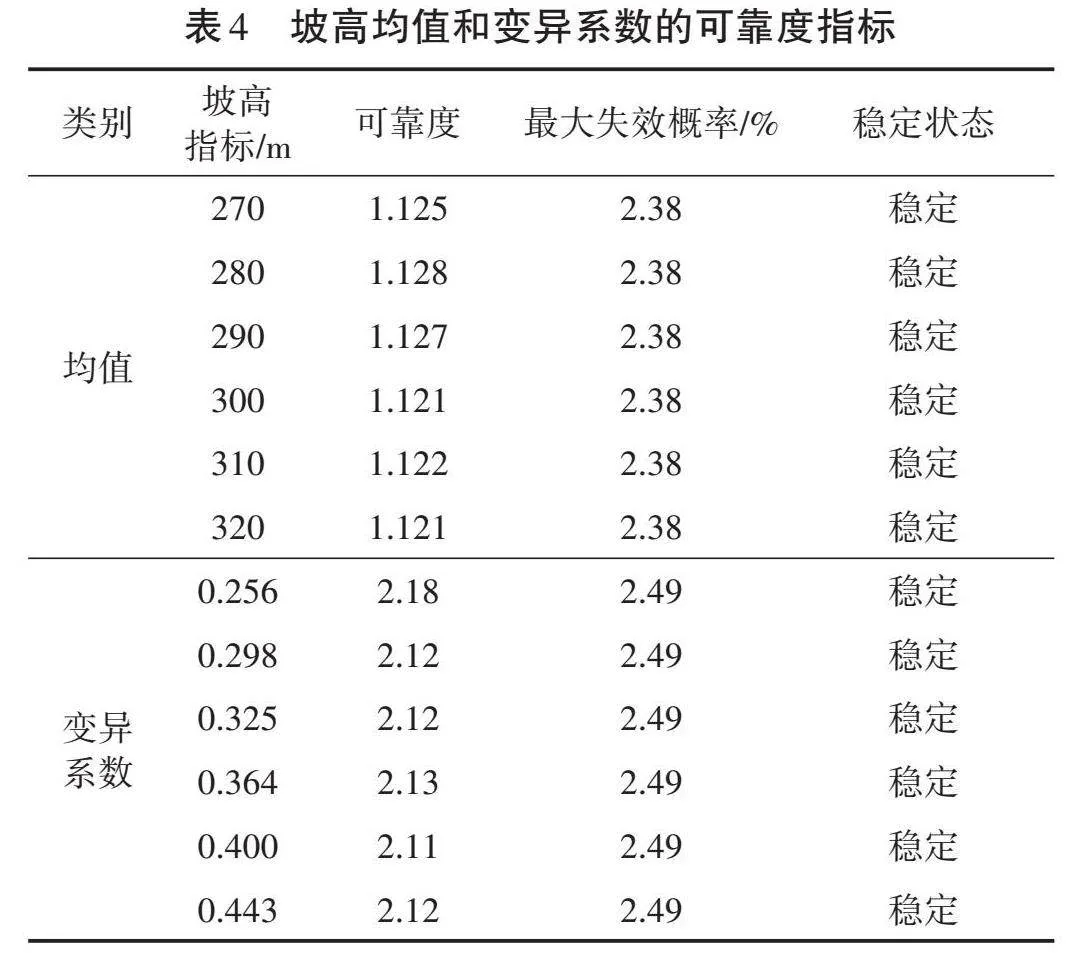
滑坡高度分别取270、280、290、300、310、320 m，变异系数为0.256、0.298、0.325、0.364、0.400、0.443，保持其余参数不变，坡高均值和变异系数的可靠度指标见表4。

由表4可知，随着岩质滑坡坡高均值的增加，其可靠度指标无明显变化，即KH=0，最大失效概率

也基本不变；同时，变异性系数的增大对滑坡的可靠度指标也几乎没有影响。因此可以得出，滑坡高度和变异性系数对滑坡稳定性及敏感性无影响。

2.3 单位长度滑坡重量与可靠度指标敏感性的关系

滑坡重量分别取950、1 050、1 150、1 250、1 350、1 450 kN，变异系数为0.022、0.034、0.045、0.058、0.062、0.073，保持其余参数不变。根据所采用的滑

坡重量均值进行计算，岩质滑坡重量均值和变异系数可靠度指标计算结果见表5。由表5可知，可靠度指标随着岩质滑坡坡度的增大而减小，几乎为线性变化，递减速率Kw=[150.85−145.381050−950]=0.05，此时最大失效概率增大，因此岩质滑坡重量增大会导致滑坡失稳可能性变大，这与实际情况相吻合。

由此可知，当滑坡重量均值增大时，可靠度指标减小；当变异系数增大时，可靠度指标虽然也会减小，但幅度相对较小，而此时最大失效概率增大，递增速率K=[1.833−1.8020.034−0.022]=0.03。通过比较得出，滑坡重量均值对岩质滑坡失稳的可靠度敏感性较大。

2.4 黏聚力与可靠度指标敏感性的关系

岩体黏聚力分别取120、130、140、150、160、170 kN，变异系数为0.113、0.125、0.137、0.159、0.168、0.179，保持其余参数不变，根据所采用的岩体黏聚力均值进行计算，岩质滑坡黏聚力均值和变

异系数可靠度指标计算结果见表6。由表6可知，可靠度指标随着岩质滑坡黏聚力的增大而减小，几乎为线性变化，递减速率Kc=[0.381−0.313130−120]=0.01，此时最大失效概率增大，因此岩质滑坡黏聚力增大会导致滑坡失稳可能性变大。

由此可知，当滑坡黏聚力均值增大时，可靠度指标减小；当变异系数增大时，可靠度指标虽然也会减小，但幅度相对较小，而此时最大失效概率增大，递增速率K=[1.957−1.8540.125−0.113]=0.08。通过比较得出，滑坡黏聚力变异系数对岩质滑坡失稳的可靠度敏感性较大。

2.5 内摩擦角与可靠度指标敏感性的关系

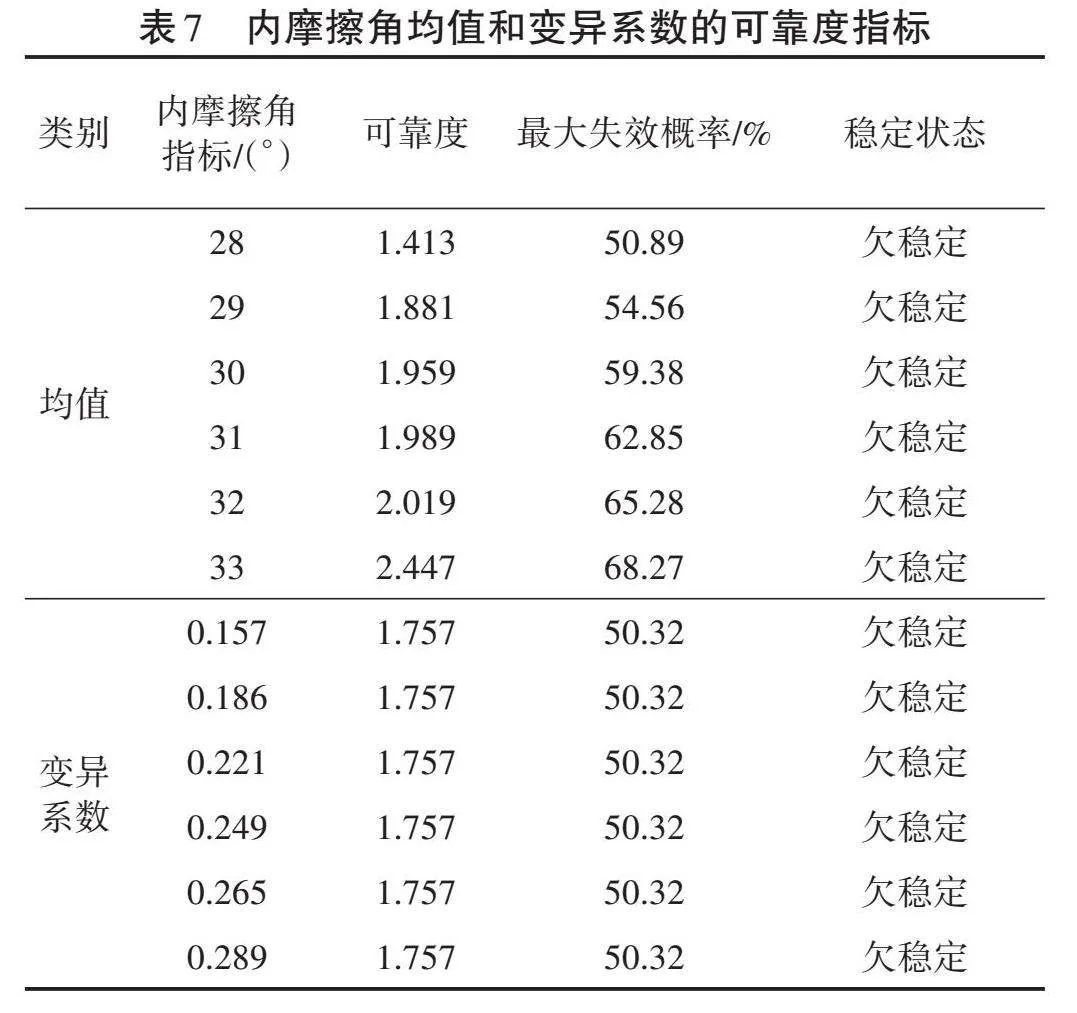
岩体内摩擦角分别取28°、29°、30°、31°、32°、33°，变异系数为0.157、0.186、0.221、0.249、0.265、0.289，保持其余参数不变，根据所采用的岩体内摩擦角均值进行计算，岩质滑坡内摩擦角均值和变异系数可靠度指标计算结果见表7。由表7可知，可靠度指标随着岩质滑坡内摩擦角的增大而减小，几乎为线性变化，递减速率Kc=[1.881−1.41329−28]=0.04，此时最大失效概率增大，因此岩质滑坡内摩擦角增大会导致滑坡失稳可能性变大。

由此可知，当滑坡黏聚力均值增大时，可靠度指标减小，此时最大失效概率增大；当变异系数增大时，可靠度指标变化不大。通过比较可以得出，滑坡内摩擦角均值对岩质滑坡失稳的可靠度敏感性较强。

3 结论

①通过对西藏旁多水利枢纽沿线典型滑坡统计分析，得出了滑坡坡度、坡高、单位长度滑坡重量、岩体黏聚力、岩体内摩擦角等参数呈正态分布。

②随着岩质滑坡坡度、重量的增大，滑坡的可靠度指标逐渐减小，失效概率逐渐增大，滑坡越不稳定；随着岩体黏聚力、内摩擦角的增大，滑坡的可靠度指标逐渐增大，失效概率逐渐减小，滑坡越稳定。

③岩质滑坡倾角的敏感性最高，其次是滑坡单位长度重量、内摩擦角和黏聚力指标；对于滑坡坡高没有表现出明显的影响规律。

参考文献：

［1］张硕，路军富，裴向军，等.坠落式危岩体稳定性可靠度判定及参数敏感性分析［J］.工程地质报，2015，23（3）：429-437.

［2］杨智翔，裴向军，袁进科.基于可靠度理论对滑移式落石的稳定性及敏感性分析［J］.科学技术与工程，2017，17（1）：285-290.

［3］李昌隆，兰措，格桑央培，等.西藏旁多水利枢纽工程对拉萨河径流情势变化的影响［J］.中国农村水利水电，2022（8）：41-49.

［4］黄扬一，向尚君.西藏旁多水利枢纽大坝沥青混凝土系统设计与运行［J］.人民长江，2021，52（2）：143-146，176.

［5］付光均，向尚君.西藏旁多水利枢纽截流施工［J］.四川水力发电，2016，35（4）：1-3，17.