晶体结构与性质考点归类分析

晶体结构与性质的相关题目往往以新科技、新能源等社会关注的热点问题为出发点，考查学生的抽象思维和逻辑推理能力，是高考的必考点之一．本文介绍了晶体结构与性质的常见题型，以提高学生对该部分内容的理解能力．

１ 考查晶胞化学式

晶胞化学式的书写，考查的是晶胞中微粒的个数，核心思想在于“均摊”．当用均摊法进行计算时，首先观察晶胞的结构，确定微粒的位置，然后运用均摊法进行计算，得出某个微粒的个数，最后写出正确的化学式．。

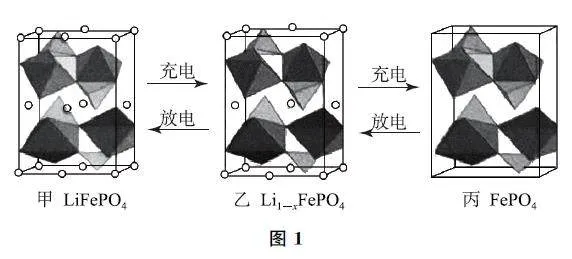
例１ LiFePO４ 的晶胞结构示意图如图１Ｇ甲所示，其中O 围绕Fe和P分别形成正八面体和正四面体，它们通过共顶点、共棱形成空间链结构，每个晶胞中含有LiFePO４ 的单元数有____个．。

电池充电时，LiFePO４ 脱出部分Li＋ ，形成Li１－xFePO４，结构示意图如图１Ｇ乙所示，则x ＝____，n（Fe２＋ ）∶n（Fe３＋ ）＝____．。

分析 本题将电化学知识和电极材料的晶体结构进行了结合，具有一定的创新性．学生解决该题的第一个思维障碍点在于如何理解LiFePO４ 晶胞结构的示意图．常规题型会对示意图中的微粒进行说明，明确微粒的具体成分，但该题并未对该部分作出阐释，仅仅给出了充放电过程中不同物质的晶胞结构示意图，需要学生对示意图中的微粒进行自主分析判断，对学生的观察理解能力有更高的要求．可以从两个方面进行思考．一是通过观察图像发现，只有“小圆球”发生了变化，其余均保持不变，且物质由LiFePO４变化为Li１－xFePO４ 再变化为FePO４，说明小圆球代表Li＋ ．二是根据题干信息“O 围绕Fe和P分别形成正八面体和正四面体”容易推知小圆球代表Li＋ ．第二个思维障碍点在于计算晶胞中“含有LiFePO４ 的单元数”．常见题型中，无论计算哪种微粒在晶胞中的个数，都能够计算出单元数．但该题只能从“Li＋ ”的微粒数进行分析，其他微粒的计算则相对较困难．根据图１Ｇ甲可知，顶点上Li＋ 数目为８×１/８＝１，面上Li＋ 数目为４×１/２＝２，棱上Li＋ 数目为４×１/４＝１，１个晶胞中含有Li＋ 的数目为１＋２＋１＝４，故每个晶胞中含有LiFePO４ 的单元数为４．据图１Ｇ乙可知，顶点上Li＋ 数目为８×１/８＝１，面上Li＋ 数目为３×１/２＝１.５，棱上Li＋ 数目为３×１/４＝０.７５，共有Li＋ 数目为３.２５，根据图１Ｇ甲、图１Ｇ乙中含有Li＋ 数列等式有１/１－x ＝ ４/３．２５，计算可得x ＝ ３/１６．图１Ｇ乙所代表物质的化学式为Li１３Fe１６（PO４）１６，则根据化合物中正、负化合价的代数和为０可知，n（Fe２＋ ）∶n（Fe３＋ ）＝１３∶３．

２ 考查晶体密度

晶体密度是高考常见的考点之一．可以按照图２所示步骤展开计算．

第１步：计算１mol晶胞的质量（均摊思想）．

１mol晶胞的质量可以写作XM ，其中X 为１个晶胞中包含化学式的个数;M 是化学式对应的摩尔质量．

第２步：计算１mol晶胞的体积．

第３步：根据公式ρ＝m/V 算出晶体密度．

在进行晶体密度计算时，需要注意单位的换算．

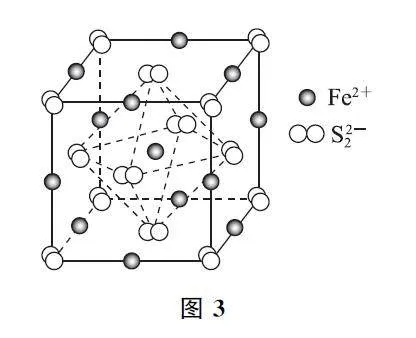
例２ FeS２ 晶体的晶胞如图３所示，晶胞边长为a nm、FeS２ 相对分子质量为M 、阿伏加德罗常数的值为N A，其晶体密度的计算表达式为____g·cm－３．

分析 第１步：计算１mol晶胞的质量．对晶胞的结构进行分析，可以发现顶点和面心位置被S２２－ 占据;棱边和体心位置被Fe２＋ 占据．则在该晶胞中，S２２－的个数为６×１/２＋８×１/８＝４;Fe２＋ 的个数为１２×１/４＋１＝４，因此，１个晶胞中含有的FeS２ 单元数为４;FeS２的摩尔质量是M ，故１mol晶胞（含４molFeS２）的质量为４M ．

第２步：计算１mol晶胞的体积．由于是立方晶胞，且FeS２ 晶胞的边长为a nm，１个晶胞的体积为（a×１０－７）３cm３，则１mol晶胞的体积为N A ×a３×０－２１cm３．

第３步：根据公式计算晶体密度ρ＝m/V ＝ ４M/N Aa３×１０－２１ g·cm－３．

３ 考查微粒分数坐标参数

在高中化学教学过程中，涉及书写微粒分数坐标参数的试题可能不会频繁出现在学生的课本和习题中，但近年高考试卷中经常出现该类题型．通常情况下，这类试题的出题方式是先给出一些相关的微粒（如离子、原子等）的分数坐标信息，接着要求学生利用微粒分数坐标参数对特定的其他微粒进行准确的位置描述．这样的题目设计旨在考查两个方面的能力：首先，考查学生是否能够有效地从题目中提取关键信息，并且理解这些信息在三维空间坐标系中的具体含义，即是否具备建立三维坐标的能力;其次，考查学生是否能够将化学知识与数学知识相结合，通过数学工具来解决化学领域中的具体问题，这反映了学生跨学科知识整合的能力．解答微粒分数坐标参数相关试题时，可以按照如下步骤进行：

第１步：根据已知微粒的坐标确定坐标系原点．

第２步：根据已知微粒坐标，确定坐标系的走向，建立三维坐标系，一般以坐标轴所在正方体的棱长为１个单位．

第３步：从微粒所在位置分别向x、y、z 轴作投影，所得坐标轴上的截距即为该原子的分数坐标．

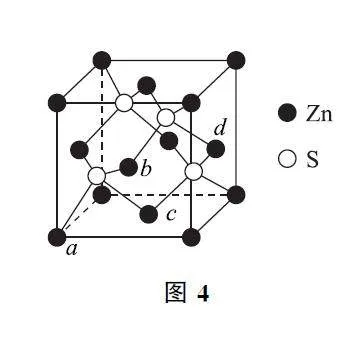
例３ S与Zn所形成化合物晶体的晶胞如图４所示．原子坐标参数可表示晶胞内部各原子的相对位置．如图４晶胞中，原子坐标参数a 为（０，０，０）;b 为（１/２，０，１/２）;c 为（１/２，１/２，０），则d 的坐标参数为____．

分析 第１步：根据已知原子的坐标确定坐标系原点．a 的坐标为（０，０，０），此为坐标原点．

第２步：建立三维坐标系．根据已知信息，可以确定三维坐标系模型如图５所示．

第３步：从原子所在位置分别向x、y、z 轴作投影，所得坐标轴上的截距即为该原子的分数坐标．根据d 的位置，可知其坐标参数为（１，１/２，１/２）．

４ 考查晶胞空间利用率

对于空间利用率的求解过程，解题思路如下：

第１步：根据“均摊法”确定晶胞中的微粒个数．

第２步：根据原子半径计算所有微粒的体积．

首先要知道每个微粒（如原子或分子）的半径．将每个微粒视为球形（对于原子而言），我们可以利用公式４πr２/３ 来计算单个微粒的体积（r 代表微粒的半径），将单个微粒的体积乘以晶胞中的微粒个数，就可以得到晶胞中所有微粒所占据的总体积．

第３步：根据晶胞参数或晶胞密度计算晶胞体积．

第４ 步：根据公式计算．（空间利用率＝晶胞占有的微粒体积/晶胞体积×１００％）

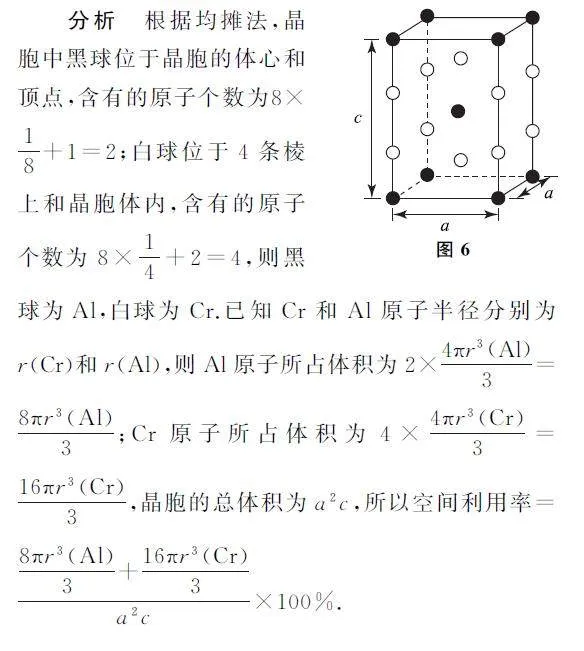
例４ AlCr２ 具有体心四方结构，如图６所示，设Cr和Al原子半径分别为r（Cr）和r（Al），则金属原子空间占有率为％___（列出计算表达式）．

５ 考查晶胞结构的投影图

原子的投影问题是最近几年试题中较新的考点，近５年高考中都有相应的考查．由于需要一定的空间想象能力和推断能力，所以也提升了晶体结构知识考查的难度．此类题有“升维”和“降维”两种考法．“降维”是以晶胞图为基础，通过观察三维图像，在三维坐标内进行投影．考查的知识点类似于数学中的“三视图”，是数学中的立体几何知识渗透化学知识的具体呈现形式．“升维”是以投影图为基础，利用投影图去分析晶胞的三维结构，通过原子在某个平面上的投影，确定原子在空间的位置．

晶体结构与性质的考点，可归结为两大类，一是数目问题，如微粒的个数、化学式、晶体的密度以及空间利用率计算等;二是结构问题，如配位数问题、分数坐标、晶胞投影、晶胞空隙等．数目问题主要考查的是晶体结构中微粒的个数和分布，以及如何根据这些信息推导出晶体的化学式和密度．对于这类问题，通常需要使用“均摊法”，即将晶胞中的微粒按照其在晶胞中的分布情况均摊到每个晶胞中，从而得到每个晶胞的微粒数目，进而计算出晶体的化学式和密度．结构问题则主要考查的是晶体结构的形状和构造，需要对晶体结构有深入的理解和分析能力，从结构入手，厘清常见晶体的结构，建立晶胞相关计算的思维模型，才能轻松应对考题．

（完）