例析水平面内圆周运动的临界问题

物体在水平面内的圆周运动的向心力可以是某一个力，也可以是几个力的合力．当物体的角速度或者线速度变化时，会引起物体受力的变化，受力的变化也会导致角速度或者线速度发生变化．物理量变化过程一般会涉及临界问题，该类问题考查的知识内容点多面广，能力要求较高，学科素养导向明显，备受命题者青睐．

１ 支持力临界

如果绳连接物体在圆锥体表面做圆周运动的向心力是绳的拉力，当物体的运动状态变化时，会引起圆锥体表面的支持力的变化，当支持为０时，往往物体的变化规律发生突变，抓住支持力为０时的物体的受力和运动特点，是解决问题的关键．

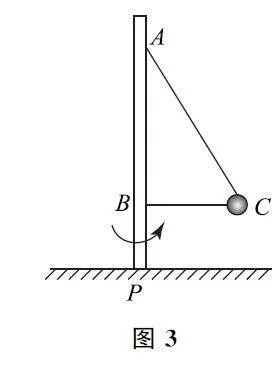
例１ 如图１所示，一个光滑的圆锥体固定在水平桌面上，其轴线竖直，母线与轴线之间夹角为θ，一条长度为l 的轻绳，一端固定在圆锥体的顶点O 处，另一端拴着一个质量为m 的小球（可看作质点），小球以角速度ω 绕圆锥体的轴线做匀速圆周运动，细线拉力F 随ω２ 变化关系如图２ 所示．重力加速度g 取１０m·s－２，由图２可知（ ）．

A．小球的角速度为２.５rad·s－１时，刚离开锥面

B．母线与轴线之间夹角θ＝３０°

C．小球质量为０.６kg

D．绳长为l＝２m

解析 根据图２可知，当小球的角速度满足ω２ ＝２５＇４rad２·s－２时，小球恰好要离开锥面，此时角速度为ω＝５／２rad·s－１，故选项A 正确．

当小球将要离开锥面时，绳子拉力与小球重力的合力提供向心力，有Fsinθ＝mω２lsinθ，即F＝mω２l．当小球离开锥面后，设绳子与竖直方向的夹角为α，绳子拉力与小球重力的合力提供向心力，有Fsinα＝mω２lsinα，即F＝mω２l，则根据图２，结合所得绳子拉力F 与ω２ 的函数关系可知，当小球离开锥面后ml＝１kgm．当小球未离开锥面时，分析小球受力情况，水平方向根据牛顿第二定律有Fsinθ－FNcosθ＝mω２lsinθ，竖直方向根据平衡条件有Fcosθ＋FNsinθ＝mg，联立可得F ＝mlsin２θω２＋mgcosθ，根据图２，结合所得函数关系可得mlsin２θ＝ ９／２５kg·m，mgcosθ＝４N，联立解得θ＝３７°，l＝２m，m ＝０.５kg．故选项D正确，选项B、C错误．

点评 细绳的拉力发生变化时，圆锥体对小球的弹力也发生变化，圆锥体与小球间弹力为０是此类问题的临界状态．

２ 细绳拉力临界

当细绳的拉力提供圆周运动的向心力时，细绳的拉力往往随物体的运动状态的变化而变化，涉及两条细绳时，哪条细绳先达到临界状态是分析的重点．

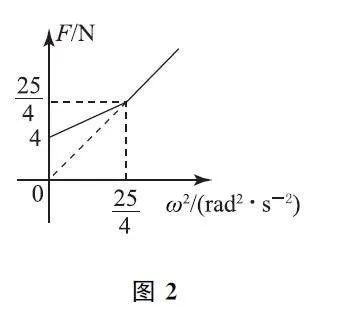
例２ 如图３所示，AP 为竖直转轴，P 端放在地面上，细绳AC 和BC 的结点C 系一质量为m 的小球，两绳能承担的最大拉力均为２.２５mg，当AC 和BC 均拉直时∠ABC ＝９０°，∠ACB ＝５３°，细绳AC 长度为L＝２ m，ABC 能绕竖直轴AP匀速转动，因而小球在水平面内做匀速圆周运动，当小球的转速增大时，两绳均会被拉断，g 取１０m·s－２，sin５３°＝0.８，cos５３°＝０.６．