计算思维与计算问题解决过程

摘要：本文以解决“计算问题”作为计算思维的核心，结合计算机科学等相关学科的教学实践，提出了一个解决计算问题的过程框架，总结了人们在解决计算问题的过程中经历的重要思维阶段和行动环节。该过程框架有助于推动对计算思维内涵的深入研究，并可以成为教师开展计算思维教学的教学模型。

关键词：计算思维；问题解决；计算问题

中图分类号：G434 文献标识码：A 论文编号：1674-2117（2024）18-0090-05

计算机科学和信息技术的发展影响了人们对计算思维的理解，以及对计算思维的教育理念和教学方式的理解。本文基于“计算思维的核心是解决计算问题”这一本质性认识，从计算理论和思维理论出发，在对与计算思维紧密相关的若干概念的辨析的基础上，结合相关教学实践，提出了计算问题解决的过程模型，讨论了该过程中影响实践的重要因素，以期为计算思维教育实践者和课程设计者提供实践思路。

计算思维概念提出的意义和价值

尽管计算思维的概念是由周以真（Jeannette Wing）教授于2006年正式提出，但是周教授也指出这个概念的首创者是MIT的认知科学家西摩尔·派普特（Seymour Papert）[1]，西摩尔·派普特于20世纪60年代发现LOGO语言编程中的问题解决思维对中小学生认知发展的影响。周教授的贡献在于用“计算思维”概念标识出计算机时代一种独特的思维过程，阐述了这种思维过程的普遍存在性，论证了在计算机无处不在的时代各行各业与计算机打交道的人都需要具备这种思维。

1.计算机学科的教育历程回顾

早期，学生对计算机学科的学习是从接受各种“计算知识”开始的[2]，其中编程语言作为人与计算机“交流”的工具，顺理成章地占据了主要地位。由于算法设计是编程的核心，所以算法研究一直是计算机科学领域的重中之重，有关算法的知识也自然而然成为教学的重点。将学习计算思维等同为掌握“算法思维”，这种认识对现在的计算思维培养和计算机科学教学仍存在深刻的影响。[3]

自20世纪80年代起，随着计算机软件的崛起和普及，人们关注的焦点转向了计算机软件的应用领域，对信息时代人才的计算机素养的教育转变为对计算工具尤其是计算机软件的学习。受此影响，我国的中小学计算机教育的主体内容也由编程语言学习（指挥计算机）转向了应用软件（以计算机为工具）的学习，典型的学习内容包括文字处理软件、幻灯片制作软件、画图修图软件等。[4]英、澳等国也将“运用技术工具处理信息资源”等内容写入信息与通信技术的课程标准。[5]然而这一“唯工具论”的教学理念很快就遇到了问题。由于计算机软件的飞速发展和频繁更新，教学内容迭代的速度明显跟不上软件产品更新换代的速度，这种“职业技能培训”式的教学目标设定，非但不能增进学生对计算机技术发展的认识，反而会让学生陷入“为学工具而学工具”的误区。[6]但是从计算机科学的角度讲，正是由于计算机软件的大力发展，系统化思维才逐渐受到重视，系统、模型、架构等概念成了学科发展的基石，这对此后计算机科学的发展产生了深远的影响，也为人们对计算思维的理解带来了新的启发。

2.计算思维的“问题解决”特性

在历经了“计算知识接受”和“认知工具应用”两个阶段后[7]，人们逐渐发现计算思维的本质是利用计算机这个工具最大化地解决问题。从思维理论上看，这一趋势也逐渐与思维的“解决问题”这一根本特性相吻合。[8]因此，了解与掌握计算机系统的工作原理，并利用计算机科学和信息技术领域的思想方法解决问题，成为计算思维教育的重要特征和价值导向[9]，计算思维的教育也步入了“普世价值推广”阶段。[10]2011年，美国国际教育技术协会（ISTE）和计算机科学教师协会（CSTA）将计算思维定义为借助计算机或相关工具解决问题的过程，并强调要将这种思维方式应用于宽泛的问题解决中。[11]在我国《普通高中信息技术课程标准（2017年版）》中，计算思维被定义为：个体在运用计算机科学领域的思想方法形成问题解决方案的过程中产生的一系列思维活动。

问题解决能力与计算思维的挂钩，已成为研究领域和教学实践领域的共识，围绕“如何培养问题解决能力”的新一轮探索已然展开。计算机科学家威廉·沃尔夫（William Allan Wulf）认为利用计算思维解决问题主要依赖于过程的处理[12]，因此算法的学习是培养计算思维的关键途径。美国数学家、计算机科学家和教育家戴维·穆尔桑德（David Moursund）等人谈到程序思维和计算思维密切相关，因此开发、表征、测试、调试，以及各自程序性的指令都是问题解决的重要方法。[13]哥伦比亚大学教授阿霍提出，构造问题解决方案的关键在于其所依赖的计算模型，因此寻找适当的计算模型用以界定问题并得出解决方案是培养计算思维的重要途径之一。[14]计算思维的提出者周以真指出“抽象与自动化”是计算思维的核心，并建议在计算思维的培养过程中应注重与工程学之间的联系。[15-16]计算机科学家罗伯特·康斯特勃（Robert Constable）则认为，计算思维不是一套静态的、有限的技能和思维过程，而是一个开放的、不断增长的“概念清单（Growing List of Concepts）”[17]，这也说明了计算思维的内涵以及培养方式会随着科学技术的发展而不断地更新。

从上面的综述中可以看出，人们对计算思维以及利用计算思维解决问题的方式有着各种各样的理解，计算思维的培养理念和方式也不尽相同。本文尝试将相关的零散观点进行组织整合，形成一个相对完整的计算问题解决过程框架，以便更好地理解和进一步研究计算思维及其内涵。

计算问题解决过程

在计算理论中，“计算问题”指的是能够在计算机上以合适的数学表达方式表示，并存在有效的解决算法的问题。[18]因此，从问题解决的角度来看，具备计算思维的学生，在遇到生活实际问题时，首先要基于对问题的理解与分析，判断其是不是一个计算问题，或者能否转化为一个计算问题。在解决计算问题时，学生会经历生成计算策略、构建计算模型、设计算法，以及借助相应计算系统实现计算作品等过程。

当学生对计算问题有了充分的理解后，就需要先概括描述问题解决的思路和步骤，包括尝试将其分解为易于控制和实现的子问题，这种有一定的抽象度的解题步骤称之为“计算策略”。[19]计算策略是学生面对计算问题时产生的初步解决思路，有时还需要借助其他学科理论知识、生活常识或经验，以及相关数据分析结果，为问题的定义和分解提供思路。计算策略的选择反映了学生对计算问题的认识与理解程度，更影响着后续计算模型的构建与算法的设计。

抽象是计算思维的本质之一，形式化又是计算思维的重要表达方式[20]，而“模型”正是对某一类别问题特定的形式化表达。因此，在确定了问题解决目标并形成了初步的计算策略后，学生就应当基于对问题的理解构建相应的计算模型。“计算模型”指的是能够对算法或程序进行规约和分析的框架，包含四个功能，即描述各功能模块如何相互连接、判定有效的算法和程序、定义给定输入的有效执行序列，以及能够计算每一模块的执行成本。[21]

概括能力是学科能力和思维能力的基础。[22]构建计算模型的过程正是学生抽象与概括计算问题特征的必要过程，也是对计算策略实施的模块化、形式化表达的过程。由于计算模型是一个由相互联系、相互作用的元素组成的集合，学生在抽象建模的过程中应以系统化的方式对其进行思考和设计。按照从整体到局部的逻辑，学生应先忽略底层交互细节，从整体上理解模型的行为和特征，识别模型的构成元素、行为、层次关系等，而后进行模块化或层次化设计。按照从内到外的角度，在计算模型的构建过程中，应先定义其边界、范围和大小，并控制复杂度，然后理解模型与外部环境的相互作用，识别模型外的关键影响因素，调整和优化模型的设计。[23]

自动化是计算思维的另一个本质。自动化是计算机最根本的特性，它离不开算法的支持。因此，在完成模型的建构之后，学生就要针对模型中的每个模块进行算法设计，而计算概念是算法设计的基础，在Brennan和Resnick提出的计算思维三维框架中，列举了七个广泛使用的计算概念，即序列、循环、事件、并行、条件、运算和数据。[24]在学习和实践的过程中，学生还会遇到更多专业、复杂的计算概念。学生在充分理解了算法的应用情境后，便可结合适用的计算概念，使用合适的方式（如流程图、伪代码等）对算法进行设计和表达，并且能够基于经验或数学理论分析效率，对算法本身及计算模型进行优化。

思维具有生产性，人们会为解决问题制作思想产品。[25]学生在完成算法设计后，就需要借助计算系统加以验证，以迭代的方式实现并完善解决方案，创造计算作品。计算系统在广义上指的是任何可以进行计算和信息处理的设备，在这里笔者将计算系统定义为解决计算问题所需要的平台，它可以是某种编程环境，也可以是某个应用程序，甚至可以是一台具体的计算机。而在创造计算作品的过程中，学生还需从功能性、可靠性、易用性等角度对计算作品进行分析和评估，并历经多次的测试调试和性能优化，甚至还需收集他人（用户）对作品的评价与反馈，才能保证计算问题被全面、有效地解决。[26]

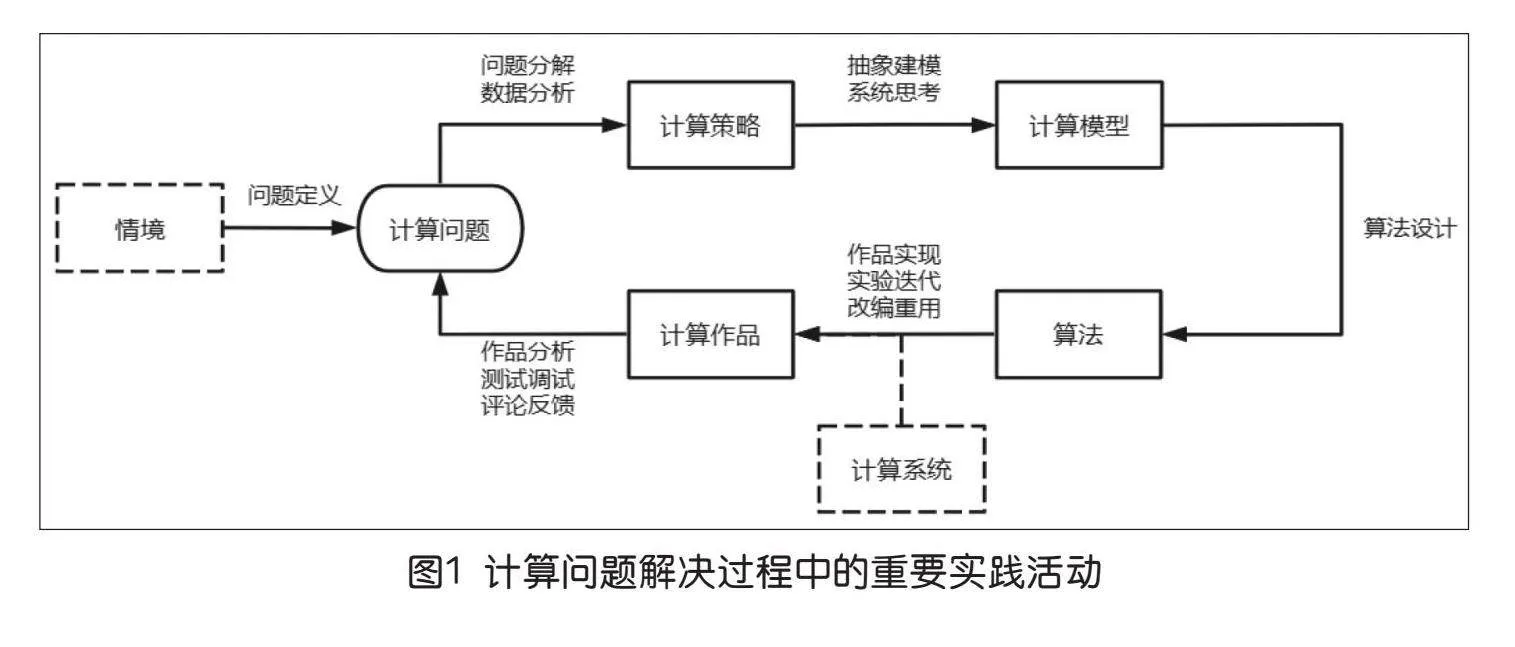
图1所示反映了计算问题解决过程中学生可能经历的重要实践活动。[27]如果说在生成计算策略时需要的是问题界定与问题分解能力，那么在构建计算模型的过程中，需要的则是抽象、概括和系统化思维能力。在算法设计与实现阶段需要对计算概念有充分的了解以便规划自动化过程。软件的调试、测试、迭代开发则体现了工程思维和系统化思维。

案例分析

下面，笔者结合实际的教学案例，详细描述如何引导学生在遇到具体问题时，有意识地思考与实施上述计算问题解决过程框架的每一步骤，在最终完成问题解决的同时，习得并强化相关的计算思维能力。本课使用某图形化编程平台作为教学工具，面向对象为小学三至四年级的学生。

在本课中，学生的任务是制作一个抽奖大转盘程序。在观看教师对已完成转盘游戏的效果演示后，学生很容易发现该程序的大致运行机制，即在有抽奖权限的玩家点击按钮后，转盘开始转动，一段时间后转盘停下，根据指针位置提示所得奖励。这样，学生在脑海中便可产生初步的计算策略，这时教师要求学生把初步的计算策略画在纸上，帮助学生明确任务完成步骤的第一级抽象，如图2（a）所示。

然后教师引导学生依序对程序中的每一个角色的行为进行完整分析。“按钮”是启动转盘的开关，当它被点击后，便会有一个被按下的动画效果，之后触发“转盘”转动，“转盘”在持续转动一段时间后，会在随机位置停下，最后根据“指针”所指位置，提示玩家所中奖品。根据上面对“按钮”“转盘”和“指针”三个角色功能和交互关系的梳理，学生便可构建出如图2（b）所示的计算模型。

接着，教师便可引导学生围绕计算模型涉及的相关计算概念，复习已知计算概念，学习新的计算概念。在掌握了必要的计算概念后，学生就能以角色为对象，在编程平台上进行编程，进行细节化的算法设计和实现，具体如图2（c）和图2（d）所示。

总结

本文围绕“计算思维的核心是解决计算问题”这一中心思想，并使用计算理论中的部分概念，构建了“界定计算问题—形成计算策略—构建计算模型—设计算法—借助计算系统实现计算作品—解决计算问题”的计算问题解决过程框架。

对于该框架在教学实践中的落地，教师和学者可以从单元设计、教学设计和教学评价方面深入探索。在单元设计方面，教师可以设置各单元的重点计算思维实践，梳理实践能力之间的进阶关联，并将它与计算思维概念结合编写进阶的能力目标。在教学设计方面，教师可以围绕图1中不同阶段可能经历的重要计算实践设计教学活动，构建思维发生发展的空间。在教学评价方面，该框架可以作为计算思维表现性评价的参考依据。但该框架目前仅围绕计算理论及计算机科学等方面展开，如何将其应用于数学、物理等自然科学的教学与研究，甚至向社会科学方向推广，仍有待进一步研究。

参考文献：

[1]Wing，J.Computational Thinking[J].Communications of the ACM.2006，49（03）：33-36.

[2][6][7][10]李锋，王吉庆.计算思维教育：从“为计算”到“用计算”[J].中国电化教育，2015（10）：6-10+21.

[3]张进宝.计算思维教育：概念演变与面临的挑战[J].现代远程教育研究，2019，31（06）：89-101.

[4][20]王荣良.中小学计算思维教育实践[M].上海：上海科技教育出版社，2019.

[5]刘敏娜，张倩苇.国外计算思维教育研究进展[J].开放教育研究，2018，24（01）：41-53.

[8][25]林崇德.我的心理学观——聚焦思维结构的智力理论[M].北京：商务印书馆，2008.

[9]李锋.中小学计算思维教育：STEM课程的视角[J].中国远程教育，2018（02）：44-49.

[11]ISTE，CSTA.Operational Definition of Computational Thinking for K-12 Education[DB/OL].[2012-04-15].https：//cdn.iste.org/www-root/Computational_Thinking_Operational_Definition_ISTE.pdf.

[12][13][15][17]National Research Council.Report of a Workshop on the Scope and Nature of Computational Thinking[R].Washing（D.C.）：The National Academies Press，2010.

[14]Aho，V.Computation and Computational Thinking[J].The Computer Journal，2012，55（07）：832-835.

[16]Wing，J.Computational Thinking and Thinking about Computing [J].Philosophical Transactions of the Royal Society，2008，366（1881）：3717-3725.

[18]Sipser，M. Introduction to the Theory of Computation （3rd ed.）[M].Boston， MA： Cengage Learning，2013.

[19][21]Bilardi，G.， & Pietracaprina，A. Models of Computation， Theoretical[M].Boston， MA： Springer，2011.

[22]林崇德.从智力到学科能力[J].课程·教材·教法，2015，35（01）：9-20.

[23][26][27]李泽，李伟，毛顿，等.计算思维实践框架研究[J].中小学信息技术教育，2021（09）：7-10.

[24]Brennan K.，Resnick M.New frameworks for studying and assessing the development of computational thinking[J].American educational research association，2012（01）：25.

作者简介：李泽，深圳点猫科技有限公司高级工程师；毛顿，深圳点猫科技有限公司高级工程师；夏立，深圳职业技术大学商务外语学院讲师。

本文为广东省教育教学成果特等奖“八微驱动、集群推进：爱加（AI+）笃行创客教育探索与实践”的阶段性研究成果；受深圳职业技术学院校级科研启动项目（6022312003S）资助。