学习支架类型对不同元认知水平学学习成绩和计算思维的影响研究

摘要：本研究旨在探讨学习支架类型对不同元认知水平学生学习成绩和计算思维的影响。温州市某小学四年级83名学生参与了为期六周的实验，被分配至实验1班（n=41）和实验2班（n=42）。实验1班的学生采用反思型学习支架进行干预，实验2班的学生则采用支持型学习支架进行干预。实验结果表明，在计算思维和元认知倾向方面，学习支架类型与元认知水平具有交互作用。对于低元认知水平学生而言，支持型学习支架比反思型学习支架更有利于提升他们的计算思维倾向和元认知倾向。然而，学习支架类型和个体元认知水平之间的交互对学习成绩没有显著影响。

关键词：计算思维；学习支架；元认知

中图分类号：G434 文献标识码：A 论文编号：1674-2117（2024）14-0021-06

引言

随着数字化时代的到来，计算思维被认为是21世纪青少年的一项重要思维技能。[1]计算思维指的是利用计算机科学的基本概念来解决问题、设计系统和理解人类行为的一系列思维活动。[2]计算思维强调通过对任务的抽象和分解，将复杂的任务逐步自动化。然而，在实际执行任务时，学生往往难以将庞大而复杂的问题拆分为若干个更易处理的小问题，这种困难影响了他们成功解决问题的能力。[3]研究表明，如果没有适当的指导，学生在发展计算思维技能方面面临着重大挑战。[4]因此，研究者认为可以给学习者提供学习支架，帮助学习者将高难度任务分解。[5]

研究证明，不同的学习支架类型对学生的影响是不相同的[6]，近期有更多的研究比较了不同学习支架类型的优势。[7]支持型学习支架能够指导学习者考虑什么以及如何将想法联系起来，反思型学习支架通过元认知问题帮助学习者澄清他们的反思过程。[8]许多研究都报道了学习支架可以提高学习者解决问题的能力，并对学习成就产生积极影响。[9]然而，他们并未证明对不同学生而言哪种学习支架类型最为有效。

此外，研究表明，由于学生元认知水平不同，学生的解决问题的能力有所差异，从而会影响到学习效果。[10]元认知水平高的学生解决问题的能力会更高，而元认知水平低的学生在问题解决活动中可能更需要帮助。因此，针对不同元认知水平的学生应该提供不同的学习支架。[8]综上所述，本研究旨在探讨学习支架类型对不同元认知水平的学生的影响差异。研究问题如下：

①学习支架类型对不同元认知水平学生的学习成绩是否有影响？②学习支架类型对不同元认知水平学生的计算思维倾向是否有影响？③学习支架类型对不同元认知水平学生的元认知倾向是否有影响？

研究方法

1.研究对象

本实验选择了温州市某小学四年级的83名学生，他们的平均年龄为11～12岁，被分配至两个班。其中一个班为实验1班（n=41），另一个班为实验2班（n=42）。学生信息均做匿名处理。

在实验班级内部，通过收集实验对象元认知倾向问卷数据进行处理，根据元认知水平的高和低将实验对象各分为两组。两个班由同一位教师授课，学习时间与课程内容相同。

2.研究背景

本实验选取了浙江省义务教育教科书四年级信息技术教材中的部分内容作为主要的学习内容。在实验过程中，支持型学习支架以提示和视觉材料的形式呈现，提供课堂知识内容和学习者需要接受的指导。反思型学习支架由探索性问题、暗示、总结等部分组成，为学习者提供了元认知问题，帮助他们回顾学习内容和反思学习过程。在为期四周的学习过程中，指导者没有提供额外的支持来控制实验。每次在完成支架的设计后，都交由具有4年教学经验的实验学校的教师进行检阅和修改。

3.研究工具

本研究采用的测量工具包括学习成绩前后测、计算思维倾向问卷和元认知倾向问卷。其中，学习成绩的前后测由笔者结合学生所学知识自主出题，试卷完成后由该领域专家和经验丰富的信息技术教师共同检阅通过，难度适合四年级学生的水平。前后测都包含10道选择题。每套题目中都含有两个反向思维题，每题10分，共计100分。前后测试题的组成结构大致相同，且难度相差不大。

计算思维倾向问卷改编自Huang，Y.和Zheng，X.开发的量表。[11]它由6道题目组成，采用5点李克特量表评分方案（非常同意、同意、一般、不同意、非常不同意）。问卷的Cronbach's alpha值为0.763。

元认知倾向问卷改编自Lai，C.-L.和Hwang，G.-J.开发的量表[12]，包含5个条目，其Cronbach's alpha值为0.757。问卷采用5点李克特量表进行评分，分值从1至5，依次代表“完全不同意”“不同意”“中立”“同意”和“完全同意”。

4.实验流程

本实验共持续六周，每周一课时，每次课45分钟。在第一周，学生需要完成前测和前问卷。从第二周至第五周，教师授课，其中，实验1班的学生采用反思型学习支架进行干预，实验2班的学生则采用支持型学习支架进行干预。在第六周，学生完成后测知识测验，并填写后测问卷。安排如图1所示。

5.数据分析方法

在本次实验研究中，收集了以下几种数据：前后测学习成绩、前后测计算思维倾向以及前后测元认知倾向。

为了区分不同元认知水平的学生，根据前问卷的元认知倾向评分，将学生分为高元认知组和低元认知组。实验1班得分高于中位数（3.8）为元认知水平高，低于的为元认知水平低；实验2班得分高于中位数（4.0）为元认知水平高，低于的为元认知水平低。

在剔除了异常情况的数据之后，收集到了实验1班高元认知水平组16个样本量，低元认知组14个样本量，1组总计样本量为30个；实验2班高元认知水平组15个样本量，低元认知组15个样本量，2组总计样本量为30个。两组共计样本量为60个。实验对象情况如表1所示。

数据分析

1.学习成绩

为了了解学习支架类型和元认知水平对学生学习成绩的影响，笔者采用了双因素协方差的数据分析方法。将学生的前测成绩作为协变量，消除学习者在学习活动前原有知识水平的差异。自变量为学习支架类型和元认知水平，因变量为学生的学习成绩。

双因素协方差分析结果如表2所示，在学习成绩方面，学习支架类型和元认知水平之间不存在显著交互作用（F=0.894，p＞0.05），说明学习支架类型和元认知水平不会共同对学生学习成绩产生显著影响。此外，学习支架类型（F=1.261，p＞0.05）和元认知水平（F=0.061，p＞0.05）对学生的学习成绩也没有显著影响。

2.计算思维倾向

为了了解学习支架类型和元认知水平对学生计算思维倾向发展的影响，本研究采用了双因素协方差分析方法。

双因素协方差结果分析如表3所示，在计算思维倾向方面，支架类型和元认知水平之间存在显著的交互作用（F=5.973，p＜0.05），两者之间的交互效应量为0.098。

进一步分析元认知水平对学生计算思维倾向的简单主效应，如表4所示。

结果表明，实验1班（F=3.658，p＞0.05）和实验2班（F=2.783，p＞0.05）学生的元认知水平在计算思维倾向方面均没有显著性差异。

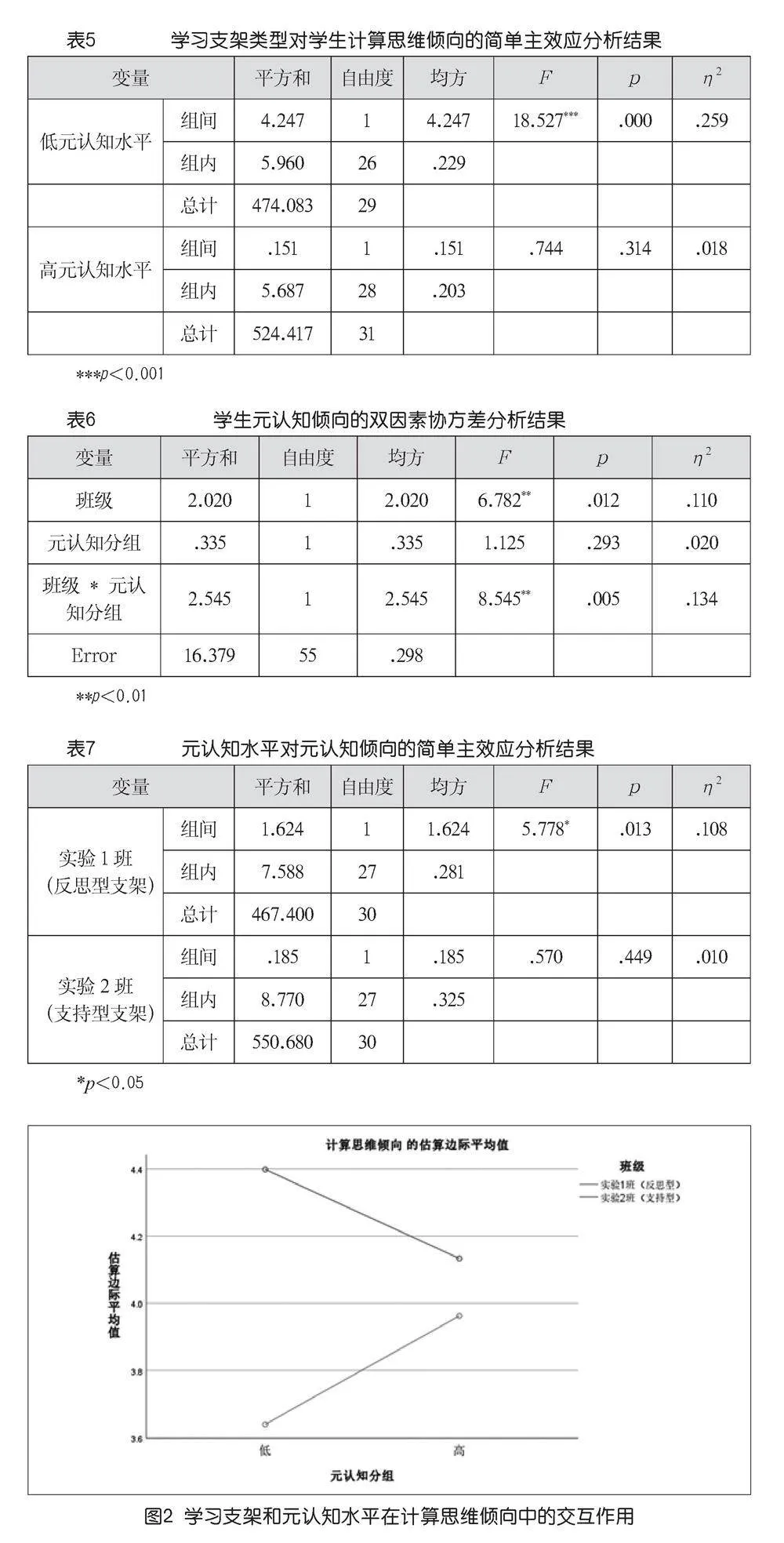
进一步分析学习支架类型对学生计算思维倾向的简单主效应，如下页表5所示。

表5为学习支架类型对学生计算思维倾向的简单主效应分析结果。低元认知水平的学生在学习过程中使用不同的学习支架，计算思维倾向发展有显著性差异（F=18.527，p＜0.001，η2=0.259）。高元认知水平的学生在学习过程中使用不同的学习支架，计算思维倾向发展没有显著性差异（F=0.744，

p＞0.05）。结果表明，相比元认知水平高的学生，学习支架更有利于元认知水平低的学生。

图2为学习支架类型与元认知水平对学生计算思维倾向影响的交互作用图。结果表明，采用支持型学习支架的学生比使用反思型学习支架的学生具有更高的计算思维倾向。此外，当使用支持型学习支架时，低元认知水平的学生的计算思维倾向发展明显高于高元认知水平的学生。

3.元认知倾向

为了了解学习支架类型和元认知水平对学生元认知倾向发展的影响，本研究采用了双因素协方差分析方法。双因素协方差结果分析如表6所示，学习支架类型对学生元认知倾向有显著影响（F=6.782，p＜0.05），效应量为0.11。同时，学习支架类型和元认知水平对学生的元认知倾向具有显著的交互作用（F=8.545，p＜0.01），两者之间的交互效应量为0.134。

进一步分析元认知水平对学生元认知倾向的简单主效应，如表7所示。实验1班不同元认知水平的学生在元认知倾向上存在显著性差异（F=5.778，p＜0.05，η2=0.108）。实验2班不同元认知水平的学生在元认知倾向上没有显著性差异（F=0.57，p＞0.05）。结果表明，在采用反思型学习支架时，高元认知水平的学生的元认知倾向明显高于低元认知水平的学生。

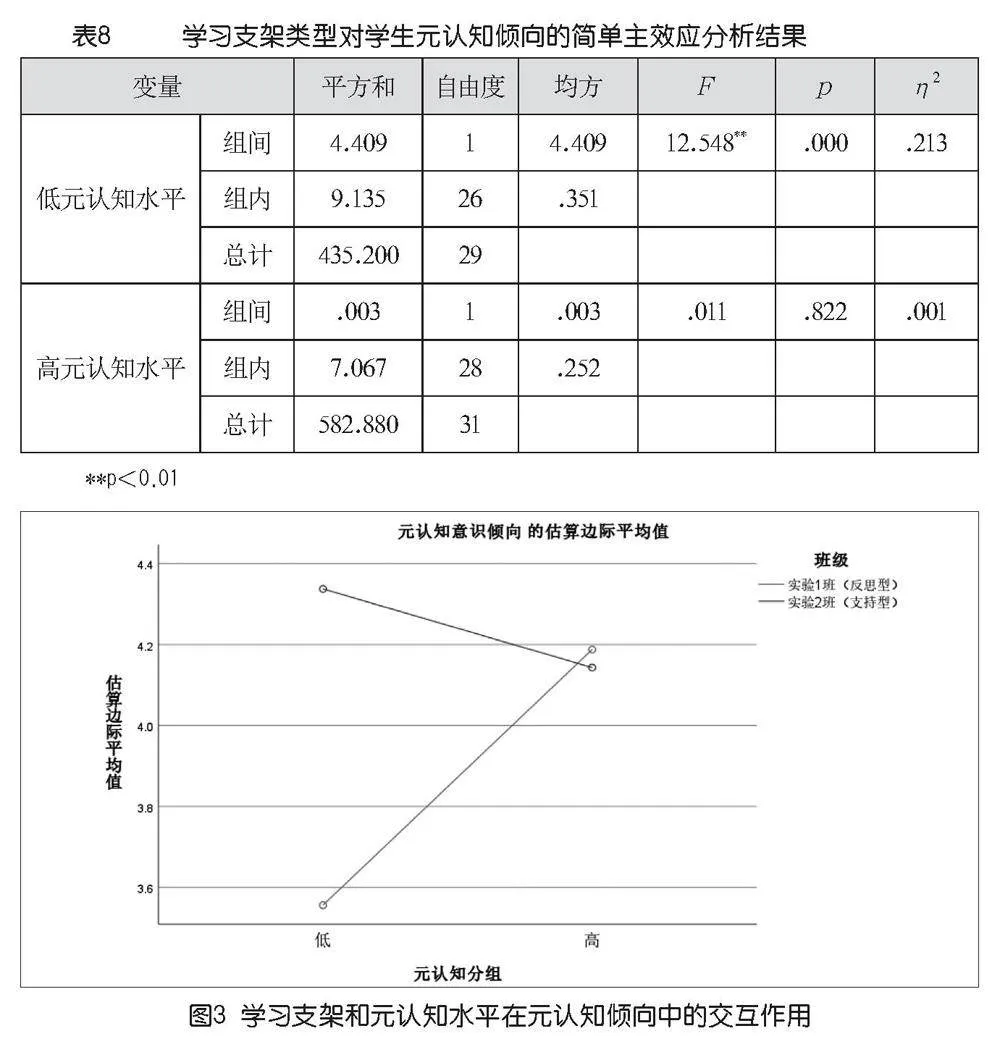
如表8所示，高元认知水平的学生在使用不同的学习支架时，元认知倾向没有显著差异（F=0.11，p＞0.05）。然而，低元认知水平的学生在使用不同的学习支架时，元认知倾向存在显著差异（F=12.548，p＜0.05，η2=0.213）。结果表明，对于低元认知水平的学生来说，使用支持型学习支架比使用反思型学习支架对提高元认知倾向更有效。

图3为学习支架类型与元认知水平对学生元认知倾向影响的交互作用图。结果表明，使用支持型学习支架的学生比使用反思型学习支架的学生有更高的元认知倾向。此外，支持型学习支架更有利于低元认知水平的学生提高他们的元认知倾向。

讨论与结论

本研究考察了学习支架类型对不同元认知水平学生的学习成绩、计算思维倾向和元认知倾向的影响。实验结果表明，在计算思维倾向和元认知倾向方面，学习支架类型与元认知水平具有交互作用。对于低元认知水平学生而言，支持型学习支架比反思型学习支架更有利于提升他们的计算思维倾向和元认知倾向。然而，学习支架类型和个体元认知水平之间的交互对学习成绩没有显著影响。

在学习成绩方面，根据研究结果，学习成绩并未受到支架类型、元认知水平以及这两者相互作用的影响。这种现象可能源于实验持续时间较短和教学课时不足，这限制了支架对学生学习干预的效果。

在计算思维倾向的发展上，分析结果显示，支架类型与元认知水平之间存在显著的相互作用。具体来说，接受支持型学习支架的学生展现出比使用反思型学习支架的学生更强烈的计算思维倾向。以往研究发现，在空间能力自我效能方面，支持型学习支架比反思型学习支架更有效，这与本研究的发现相呼应。[6]因此可以推断，支持型学习支架对于促进学生计算思维倾向的发展起到了更为关键的作用。

在元认知倾向方面，研究结果揭示，支架类型与元认知水平具有显著的交互作用。这表明通过使用学习支架可以有效地促进学生元认知思维的提升。因此，学习支架可以成为学生促进元认知活动的有效策略，通过提供解释性问题，在学习过程中诱导计划、监控和评估，帮助学生学习特定领域的知识。[13]另外，进一步的比较分析发现，相较于反思型学习支架，支持型学习支架更能促进学生元认知倾向的发展，尤其是在低元认知水平的学生群体中，其元认知倾向的提高更为明显。学者Jeon，H.J.在研究中发现，学习支架通过使学生专注于重要信息来促进元认知思维，低元认知组的学生在接受关于支持型的支架时表现更好，这与本文研究发现相符。[14]

当然，本研究也存在一些局限性。首先，本研究的样本总量较小，这可能导致实验结果代表性弱，后续研究可以扩大样本量。其次，本实验的实验周期较短，对于习惯传统模式教学的学生来说，支架的干预作用并不明显，从而使某些方面的实验结果并不显著。建议未来的研究者考虑延长实验时间，以增强支架对学生学习过程的干预效果。

参考文献：

[1]Bocconi，S.，Chioccariello，A.，Kampylis，P.，Dagiene，V.，Wastiau，P.，Engelhardt，，& K.，E.，J.，Horvath，M.A.，Jasute，E.，Malagoli，C.，

Masiulionyte-Dagiene，V.and Stupuriene，G.Reviewing Computational Thinking in Compulsory Education，2022.

[2]Wing，J.M.Computational thinking[J].Communications of the ACM，2006，49（03）：33-35.

[3]Tikva，C.，Tambouris，E.The effect of scaffolding programming games and attitudes towards programming on the development of Computational Thinking[J].Education and Information Technologies，2022，28（06）：6845-6867.

[4]Denner，J.，Werner，L.，Ortiz，E.Computer games created by middle school girls： Can they be used to measure understanding of computer science concepts？[J].Computers & Education，2012，58（01）：240-249.

[5]Zhou，Y.，Chai，C.S.，Li，X.ect.Application of Metacognitive Planning Scaffolding for the Cultivation of Computational Thinking[J].Journal of Educational Computing Research.2023，61（06）：1123-1142.

[6]Atman Uslu，N.，Yildiz Durak，H.，Ay，G.M.Comparing reflective and supportive scaffolding in 3D computer‐aided design course： Engineering students' metacognitive strategies，spatial ability self‐efficacy，and spatial anxiety[J].Computer Applications in Engineering Education，2022，30（05）：1454-1469.

[7]Kim，N.J.，Vicentini，C.R.，Belland，B.R.Influence of Scaffolding on Information Literacy and Argumentation Skills in Virtual Field Trips and Problem-Based Learning for Scientific Problem Solving[J].International Journal of Science and Mathematics Education，2021，20（02）：215-236.

[8]Kim，J.Y.，& Lim，K.Y..Promoting learning in online，ill-structured problem solving： The effects of scaffolding type and metacognition level[J].Computers & Education，2019，138（SEP）：116-129.

[9]Joo-Yeun，K.L.，Kyu Yon.The effects of scaffolding types on problem solving ability and achievement in problem solving learning with creative thinking method[J].Journal of Korean Association for Educational Information and Media，2015.

[10]Huang，Y.，Zheng，X..Effects of Scaffolding Types and Individual Metacognition Levels on Learning Achievement in Online Collaborative Argumentation，2021.

[11]Hwang，G.-J.，Li，K.-C.Trends and strategies for conducting effective STEM reseGwo-Jen Hwang arch and applications： a mobile and ubiquitous learning perspective，2020.

[12]Lai，C.-L.，& Hwang，G.-J.Effects of mobile learning time on students’ conception of collaboration，communication，complex problem-solving，meta-cognitive awareness and creativity，2014.

[13]Lee，S.Effects of Scaffolding and Metacognition and Collaborative Preference on Problem-solving in Blended Collaborative Learning.Korean Association for Educational Information and Media[J].2017，23（01）83-108.

[14]Jeon，H.J.The effects of learner's metacognition and scaffolding types on problem solving process in web‐based PBL，2007.