光滑曲面上绳子或链条张力的确定
2024-07-13王伟民辛存良
王伟民 辛存良
摘 要:采用微积分的方法对一道涉及光滑的定滑轮上静止绳子中张力的问题进行解析;推导沿高度递增的光滑斜面拉动质量分布均匀的绳子需要的拉力公式,以例题解答的方式阐述这一公式在解决相关问题中的应用。
关键词:均质绳;光滑曲面;张力
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2024)6-0070-4
将有质量的绳子或链条放在高度递增的光滑曲面上,在其最上端施加外力使其保持平衡状态,若绳子或链条的各部分都紧贴在曲面上,由于其自身重力的作用,绳子或链条有沿曲面下滑的趋势,使得各部分相互牵拉而产生张力。因为绳子或链条与光滑曲面之间只存在正压力,不存在摩擦力,所以,对平衡状态下的绳子或链条,当其下端受到沿曲面切线方向向下的拉力,绳子或链条各部位依然紧贴曲面的情况下,这个额外施加的力会大小不变地“传递”到绳子或链条的各点——即绳子或链条各点的张力都比原来多出了这个增加的拉力。利用这一规律和相关条件,可以求解绳子或链条各点张力的大小。
1 对一道力学题目的解析
例题1 质量为m、长为l的均匀绳,搭在半径为R的光滑的定滑轮上,如图1所示,求绳中的最大张力[1]。
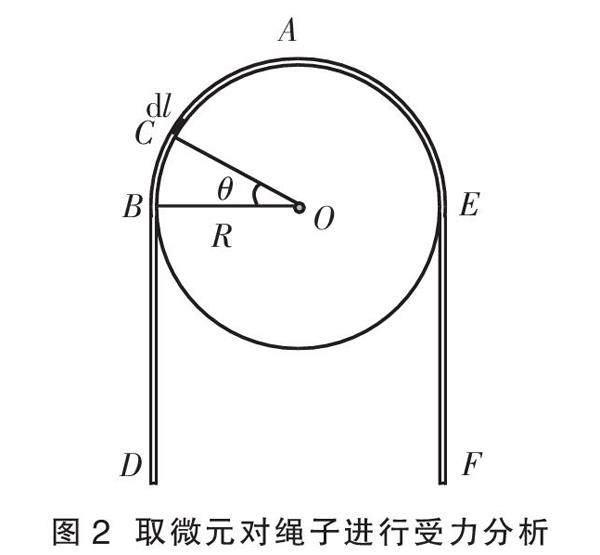
分析 因为绳子质量分布均匀,滑轮是光滑的,所以绳子搭在滑轮上能够保持静止状态时,滑轮两边绳子的长度必须是相等的。显然,这种状况下绳子张力最大的位置在其最高点,即图2中的A点,因此,我们只需确定该点绳子的张力即可。本题解法较多,下面先采用微积分的方法进行求解。
解析 如图2所示,C点是压在光滑滑轮边缘圆弧型绳子上的任意一点,OB是滑轮的水平半径,设∠BOC=θ。依题意可知,绳子的线密度为ρ=m/L。在C点的上方取一段微圆弧绳子dl,它所对的圆心角为dθ,那么这段微圆弧绳子的质量为
dm=ρdl=(m/L)Rdθ
在光滑滑轮上,沿滑轮边缘的切线方向单独牵拉这段微圆弧绳子并保持平衡时需要的拉力为
我们可否避开微积分方法,采用中学的知识进行求解呢?
2 沿光滑曲面匀速拉动绳子需要的拉力
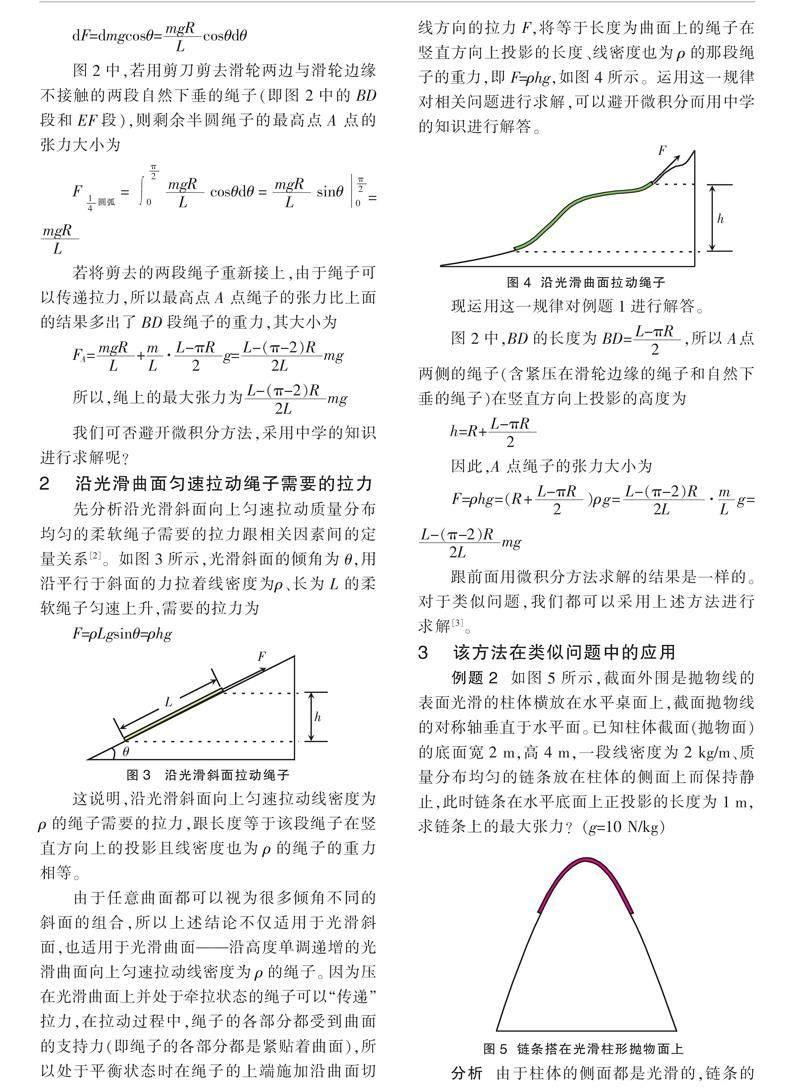
先分析沿光滑斜面向上匀速拉动质量分布均匀的柔软绳子需要的拉力跟相关因素间的定量关系[2]。如图3所示,光滑斜面的倾角为θ,用沿平行于斜面的力拉着线密度为ρ、长为L的柔软绳子匀速上升,需要的拉力为
F=ρLgsinθ=ρhg
这说明,沿光滑斜面向上匀速拉动线密度为ρ的绳子需要的拉力,跟长度等于该段绳子在竖直方向上的投影且线密度也为ρ的绳子的重力相等。
由于任意曲面都可以视为很多倾角不同的斜面的组合,所以上述结论不仅适用于光滑斜面,也适用于光滑曲面——沿高度单调递增的光滑曲面向上匀速拉动线密度为ρ的绳子。因为压在光滑曲面上并处于牵拉状态的绳子可以“传递”拉力,在拉动过程中,绳子的各部分都受到曲面的支持力(即绳子的各部分都是紧贴着曲面),所以处于平衡状态时在绳子的上端施加沿曲面切线方向的拉力F,将等于长度为曲面上的绳子在竖直方向上投影的长度、线密度也为ρ的那段绳子的重力,即F=ρhg,如图4所示。运用这一规律对相关问题进行求解,可以避开微积分而用中学的知识进行解答。
现运用这一规律对例题1进行解答。
跟前面用微积分方法求解的结果是一样的。对于类似问题,我们都可以采用上述方法进行求解[3]。
3 该方法在类似问题中的应用
例题2 如图5所示,截面外围是抛物线的表面光滑的柱体横放在水平桌面上,截面抛物线的对称轴垂直于水平面。已知柱体截面(抛物面)的底面宽2 m,高4 m,一段线密度为2 kg/m、质量分布均匀的链条放在柱体的侧面上而保持静止,此时链条在水平底面上正投影的长度为1 m,求链条上的最大张力?(g=10 N/kg)
分析 由于柱体的侧面都是光滑的,链条的质量分布均匀,所以静止于柱体侧面上的链条必然关于抛物线的对称轴对称,且抛物线顶点处链条的张力最大。因此,只要能够确定抛物线两侧的链条在竖直方向上投影的长度,根据题目给出的链条线密度的条件,即可求解最高点链条的张力。
F=ρhg=2 kg/m×1 m×10 N/kg=20 N
即,链条上的最大张力为20 N。当然,本题也可以用微积分的方法进行求解。不过,相比于直接运用公式F=ρhg的求解方法,采用微积分的方法进行解答的过程较为复杂。
例题3 如图7所示,表面光滑的圆柱体横放于水平地面上,其截面半径R=0.8 m(图中为圆柱体的横截面,O是截面圆的圆心)。A、B为两个半径都是r=0.2 m金属球的球心,A、O、B三点在同一水平线上,A'C、B'D是两根轻质无弹性细线,将两个金属球与一段质量分布均匀的软绳(图2中压在圆弧CD上的绳子)的两端相连接,且C、D两点是细线A'C和B'D与圆O相切的切点。两金属球的质量均为0.4 kg,圆弧绳子的线密度为ρ=1 kg/m。试求绳上的最大张力。(取g=10 N/kg)
分析 系统稳定后,A金属球受到自身重力、圆柱体对其水平向左的支持力和绳子对球的拉力这三个力的作用(B金属球的受力情形类似,不再重复分析),其中球的重力及细线拉力的示意图如图8所示。因为圆柱体的侧面是光滑的,CD段绳子及两个金属球的位置都是关于圆柱体的竖直直径对称,所以圆弧绳子最高点E处的张力最大,大小等于跟圆弧在竖直方向上投影长度对应、同样线密度绳子的重力与细线AC对C的拉力(也等于对A的拉力)之和。因此,根据题目条件,只要能够确定细线对金属球拉力的大小和弓形的高EH即可。
因为OH=Rcos∠COH=Rcos∠OAC=0.48 m,所以EH=OE-OH=0.32 m。
因此,绳子最高点E处的张力大小为
F=T+ρg·EH=5 N+1 kg/m×0.32 m×10 N/kg=8.2 N
所以,绳子上的最大张力为8.2 N。
4 结 语
高度单调递增的光滑曲面上放置的质量分布均匀的绳子(或链条)保持平衡状态,或对其施加外力使其保持平衡状态,如果绳子(或链条)上的各部分都是紧压在曲面上,那么,由于自身重力而使绳子(或链条)上某点产生张力,张力的大小等于曲面上跟该点下方的绳子(或链条)在竖直方向上投影长度相等的同样线密度的绳子(或链条)的重力。利用这一规律并结合相关条件,可以方便、快捷地求解光滑曲面上绳子的张力问题。
参考文献:
[1]杨榕楠.更高更妙的物理:高考高分与自主招生决胜篇(第二版)[M].杭州:浙江大学出版社,2018.
[2]王伟民,牟银勇.等时圆——求解物体沿光滑斜面滑行问题中的桥梁[J].物理教学探讨,2023,41(2):61-64.
[3]曹鹏,李力.任意光滑曲面上静止均质链所需拉力与总支持力的计算[J].物理教师,2017,38(6):61.
(栏目编辑 蒋小平)
收稿日期:2023-09-15
作者简介:王伟民(1964-),男,中学高级教师,主要从事中学物理教学研究。
*通信作者:辛存良(1977-),男,中学高级教师,主要从事中学物理教学研究。
