基于气象观测数据建立卷积神经网络算法反演PM2.5
2024-06-28王雨轩周甘凝许文龙秦孟晟
王雨轩 周甘凝 许文龙 秦孟晟

收稿日期:2023-11-10
基金项目:江苏省青年基金项目(KQ202330)。
作者简介:王雨轩(1993—),男,扬州宝应人,助理工程师,主要从事气溶胶、大气探测研究。
摘 要:利用扬州市气象观测站点和中国环境监测总站的逐小时数据估算PM2.5的各相关组合因子,然后利用CNN卷积神经网络算法构建反演PM2.5质量浓度的机器学习模型。结果表明:(1)利用 CNN卷积神经网络算法反演PM2.5是有效且可行的,且比一般的线性回归算法效果更佳,为反演PM2.5提供了一种新的机器学习方法。(2)在影响PM2.5反演的各输入变量因子中,PM10与能见度变量为高相关因子。利用神经卷积网络算法反演PM2.5理论上反演精度能够随着输入信息增多而不断提高。
关键词:CNN卷积神经网络算法;气象观测数据;PM2.5
中图分类号:P407.7 文献标识码:B文章编号:2095–3305(2024)03–0-03
PM2.5是指悬浮在空中的空气动力学当量直径≤2.5 μm的细颗粒物,其严重影响环境、气候,危害人体健康,破坏生态系统[1]。在排放源相对稳定的情况下,气象因素也是污染物形成、传输及沉降等环节的重要原因[2-3]。因此,从气象学的角度分析大气污染的规律和机制,有助于为大气污染防治提供科学支撑。尽管环境监测站点对近地面PM2.5直接测量的精度较高,但在监测点的数量和分布上的局限性较大,只能反映监测站点小范围内PM2.5的变化。因此,有必要利用气象观测数据对PM2.5乃至其他一些常见的大气污染物进行模拟反演,继而能大范围地揭示常见大气污染物的时空变化规律。
气象要素对PM2.5的形成起着促进或改善作用[4]。魏文静等[5]对山东省17个地市的研究表明,PM2.5受气温和降水的影响较为显著;黄小刚等[6]研究表明,气象对PM2.5污染有一定调节作用,PM2.5与气温、风速、湿度和降水量呈线性递增或递减关系。
前人针对PM2.5也开展了多途径的反演,一般较常用的方法是多元线性回归法。相关学者利用多元线性回归模型分析2014年APEC和2015年国庆阅兵期间气象要素对PM2.5的影响;何钰清等[7]利用多元线性回归分析法建立了PM2.5月均浓度的预测模型。但颗粒物浓度的变化与气象条件之间呈现很强的非线性关系,因此,传统的多元线性回归模型预测PM2.5质量浓度的局限性较大[8]。
近年来,随着机器学习技术的发展,已有不少学者利用神经网络算法来估算PM2.5。陈兵红等[9]应用多元线性回归和随机森林方法反演浙江省PM2.5浓度;石灵芝等[10]运用BP人工神经网络预测短期的PM10小时数据;胡娟等[11]尝试从遥感的角度利用BP神经网络算法反演PM2.5;还有学者基于随机森林算法的气象归一化方法评估了全球11个城市2020年初的PM2.5、O3等浓度的变化情况。机器学习基于统计学原理,理论上只要输入的信息越多越详细,神经算法的效果就越好。不同于以往传统的对复杂的大气污染的物理化学过程和卫星遥感原理的研究,神经网络算法为PM2.5的反演提供了新途径。
1 数据来源及算法原理
1.1 数据来源
聚焦扬州地区,大气污染数据来源于中国环境监测总站,包括PM2.5和PM10,使用其逐小时数据计算日平均值。相应的气象数据来源于扬州市气象局自动观测站监测数据。时间段为2018年1月1日—2022年11月30日。其中,2020年2月1日—6月30日数据缺失,不在研究范围内。
1.2 算法原理
1.2.1 卷积神经网络算法
卷积神经网络(Convolution Neural Networks,CNN)
最早由Yann LeCun等提出。CNN 卷积神经网络是一种包含卷积计算且有深度结构的前馈神经网络,是深度学习算法代表之一[12]。近年来,随着机器学习方法的不断发展,CNN卷积神经网络算法也逐渐被应用于大气科学领域。 典型的CNN网络结构主要包含输入层、隐含层和输出层(图1)。其中,隐含层主要包含卷积层、池化层和全连接层。数据通过输入层后,依次在各个神经网络层传递,每一网络层都能够获取对平移、缩放和旋转不变的观测数据的显著特征。隐含层的主要作用是实现特征提取。
1.2.2 多元线性回归
多元线性回归模型(MLR)是应用较为广泛的统计方法,可用于研究因变量与多个自变量之间的关系。建立多元线性回归模型可较好地解释以及估计因变量的值,其一般形式为:
Y=β0+β1x1+β2x2+…+βmxm+ε(1)
式(1)中,Y为因变量,x1,x2,…,xm为自变量,β0,
β1,…,βm为回归系数,ε为随机误差。
1.2.3 模型变量选择及评价指标
尝试建立基于气象观测数据的卷积神经网络算法(CNN)反演PM2.5的模型,输入气象观测数据,随机挑选输入的日数据的70%作为神经网络训练集,30%作为结果对比集。反演精度评价指标包括:
均方根误差(Root Mean Squared Error,RMSE)。
RMSE=(2)
均方绝对百分比误差(Mean Absolute Percentage Error,MAPE)。
MAPE=||(3)
决定系数(Coefficient of Determination,R2)。
(4)
(5)
式(2)~式(5)中,为PM2.5实测值,为多元线性回归MLR或卷积神经网络CNN反演得到的PM2.5。
2 结果与分析
2.1 PM2.5反演模型的建立
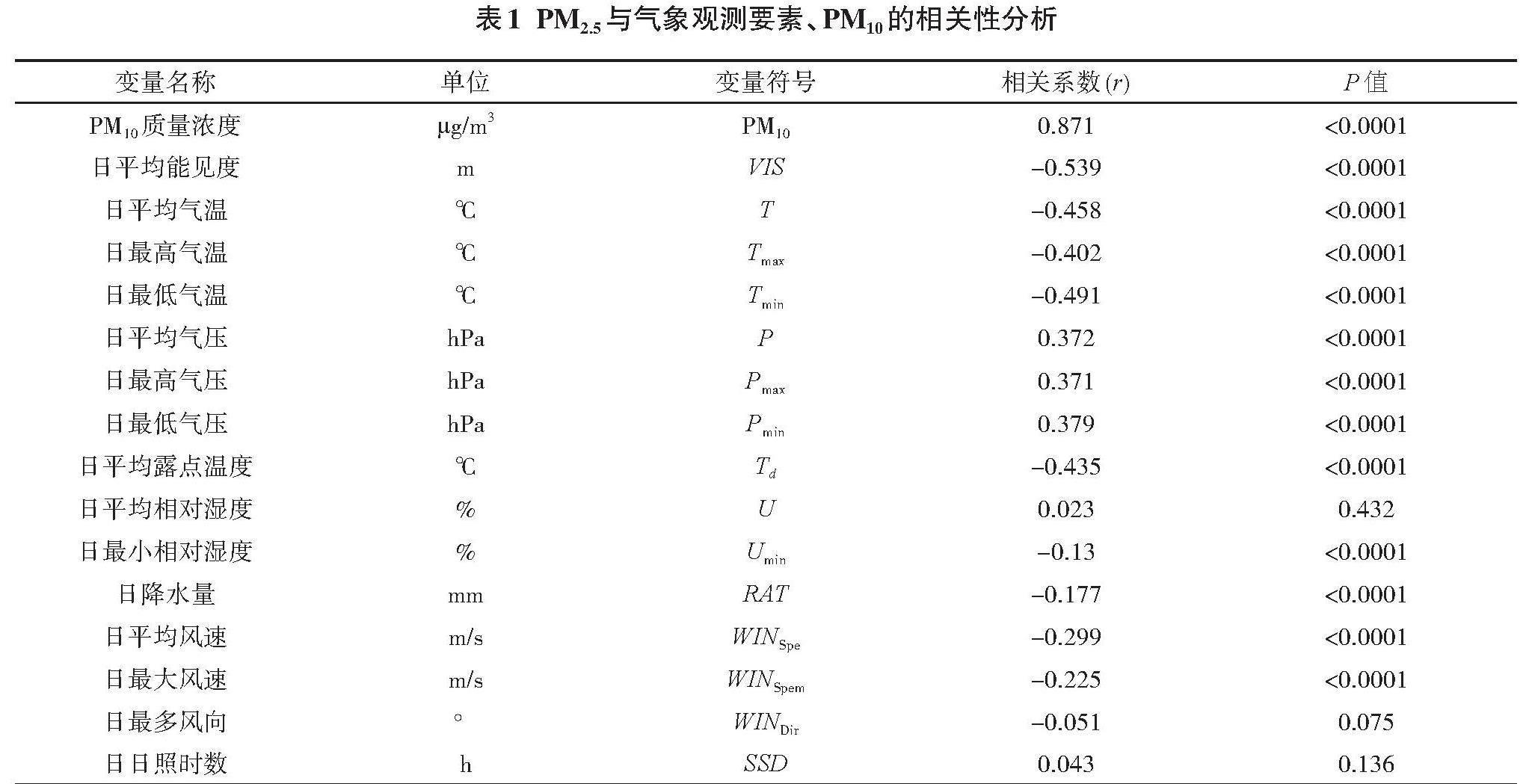
输入参数包括PM10、能见度、温度系列参数、气压系列参数、相对湿度系列参数,露点温度、风向风速系列参数、降水量和日照时数(表1)。利用皮尔逊相关系数r估计变量x,y间的相关性。r值介于[-1,1],r>0表示正相关,即两变量同向相关,反之表示两变量异向相关。r绝对值越接近1,表示两变量的关系越密切;越接近0,表示两变量的关系越不密切。表1是各变量因子与PM2.5的相关系数r和显著性水平P。该表可以反映出,与PM2.5相关性较大的变量为PM10、VIS。其中,PM10、P、Pmax、Pmin、U、SSD这6个变量与PM2.5呈正相关关系,剩下的10个变量与PM2.5呈负相关关系。还可以发现,除了U、WINDir和SSD,其余变量均在0.01水平(双侧)上相关性显著。
2.2 CNN与MLR反演性能对比
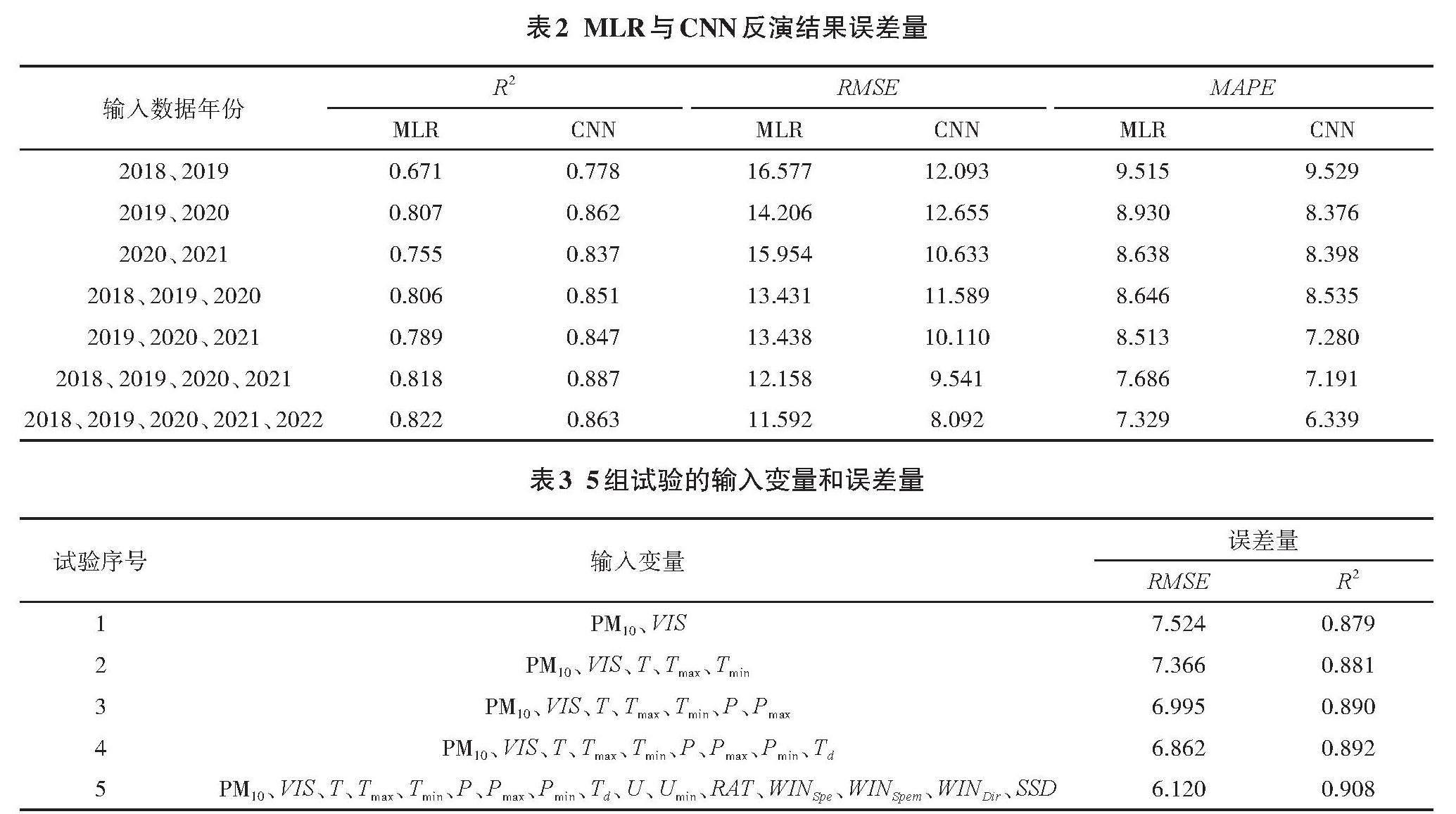
基于上述建立的PM2.5反演模型,输入变量首先采用“试验5”的变量组合(表3),CNN和MLR的反演结果对比见表2。其中,按输入数据的年份分为2年期、3年期、4年期和5年期。首先可以整体性地看出,MLR的R2值均小于CNN的R2值,MLR的RMSE和MAPE均大
于CNN的RMSE和MAPE,说明CNN的反演精度要优于MLR。然后对2年期的3组数据和3年期的2组数据取平均。
2年期的3组数据平均值为:
MLR:R2=0.744,RMSE=15.579,MAPE=9.028;
CNN:R2=0.826,RMSE=11.794,MAPE=8.768。
3年期的2组数据平均值为:
MLR:R2=0.798,RMSE=13.435,MAPE=8.580;
CNN:R2=0.849,RMSE=10.850,MAPE=7.908。
由此可以看出,随着输入数据年份数的增加,CNN
和MLR的反演性能指标都在提升,其中,R2值随着年份数的增加而增大,RMSE和MAPE随着年份数的增加而减小。表明反演的相关性不断提升,误差不断减小,精度有所提高。因此,若能有长时间的年份数据作为神经网络的训练集,反演的PM2.5理论上十分接近实际的PM2.5。
2.3 CNN模型输入参数的分析
在验证CNN模型的反演精度后,有必要对CNN模型的输入参数做研究,探讨各输入参数对反演精度的影响情况。考虑依次增加输入参数,即“试验1”至“试验5”(表3)。由于PM10和能见度VIS与PM2.5的相关性较大,因此,将其作为基本的输入参数,即“试验1”,后依次增加温度系列参数、气压系列参数、露点温度,即“试验2”至“试验4”,“试验5”包含研究全部的气象观测数据参数。从反演的误差结果可以看出,随着输入参数的不断增加,RMSE值不断减小,R2值不断增加,说明反演精度不断提高,这也与上述介绍的机器学习的特性相对应:理论上,输入的信息越多,机器学习的效果越好。
3 结论
(1)利用 CNN卷积神经网络算法反演PM2.5是有效可行的,且比一般的线性回归算法效果更好,为反演PM2.5提供了一种新的机器学习方法。
(2)在影响PM2.5反演的各输入变量因子中,PM10与能见度变量为高相关因子。利用神经卷积网络算法反演PM2.5理论上反演精度能够随着输入信息增多而不断提高,具体有待进一步研究。
参考文献
[1] 郭新彪,魏红英.大气PM2.5对健康影响的研究进展[J].科学通报,2013,58(13):1171-1177.
[2] 余钟奇,马井会,毛卓成,等.2017年上海臭氧污染气象条件分析及臭氧污染天气分型研究[J].气象与环境学报, 2019,35(6):46-54.
[3] 严文莲,刘端阳,康志明,等.江苏臭氧污染特征及其与气象因子的关系[J].气象科学,2019,39(4):477-487.
[4] 冯万富,沈新志,周继良,等.基于气象要素的鸡公山景区PM10浓度预测[J].河南大学学报(自然科学版),2022,52(5): 571-578.
[5] 魏文静,谢炳庚,周楷淳,等.2013—2018年山东省大气PM2.5和PM10污染时空变化及其影响因素[J].环境工程, 2020,38(12):103-111.
[6] 黄小刚,赵景波,孙从建,等.汾渭平原PM2.5空间分布的地形效应[J].环境科学,2021,42(10):4582-4592.
[7] 何钰清,李磊,杨红龙,等.深圳PM2.5浓度变化趋势及其月尺度预测方法[J].科学技术与工程,2022,22(1):400-408.
[8] 刁一伟,王红磊,沈利娟,等.2015—2021年南京市大气污染特征及污染个例研究[J].环境科学研究,2023,36(2):260-272.
[9] 陈兵红,靳全锋,柴红玲,等.浙江省大气PM2.5时空分布及相关因子分析[J].环境科学学报,2021,41(3):817-829.
[10] 石灵芝,邓启红,路婵,等.基于BP人工神经网络的大气颗粒物PM10质量浓度预测[J].中南大学学报(自然科学版),2012,43(5):1969-1974.
[11] 胡娟,郑军,许文龙,等.利用多源数据建立GA-BP算法模型估算PM2.5的研究[J].气象科学,2021,41(3):314-322.
[12] 姚姝含,官莉.基于星载红外高光谱观测用机器学习算法反演大气温湿廓线[J].红外与激光工程,2022,51(8):461-472.
