对比教学：促进学生的乘法分配律模型建构

朱绮琳

［摘要］ 乘法分配律变式较多，是小学数学运算律教学中公认的难点；突破这一难点的有效方式不是反复操练，而是帮助学生建立概念的基本模型，加深对概念原型的理解。以苏教版四年级下册“乘法分配律”教学为例，通过横向对比、纵向对比、交叉对比，指出乘法分配律的核心切入点和路径，以帮助学生建立清晰的概念结构与模型建构，形成灵活应用的思路方法。

［关键词］ 小学数学；乘法分配律；对比教学；模型建构；数学变式

乘法分配律是运算律教学中公认的难点。为什么呢？因为它变式多且复杂，加之四年级的学生在“观察”能力的精细度上本身有所欠缺。针对这样的情况，课堂上教师常常会抓住各种变式，让学生反复操练，但往往“力倍功半”。其实，变式越多，越要明晰概念的基本模型，加深对概念原型的辨识度。只有这样，当学生面对各种变式时，才能将它与“原型”对接，甚至是将它变回“原型”，这样的学习过程学生经历的是一次次“转化旅程”，尤其是在数系扩张时，学生才能顺利地实现“理”与“法”的转化与迁移。基于以上分析，笔者在课堂实践中着重采用对比教学法，从多个维度、不同路径加深学生对“乘法分配律”概念的理解。

一、横向对比，厘清“乘法结合律”和“乘法分配律”的模型

在实际应用中，“乘法结合律”和“乘法分配律”最容易发生混淆，为了加强概念原型的认识和方法的指导，我们设计了一些合理的变式练习，有针对性地帮助学生形成一些简算方法与策略，提高其运算能力。

出示三题计算，让学生独立完成，学生呈现出如下的作业情况：

师：第二题可以简便计算吗？你怎么看出来的？

生1：可以，算式中有25和4，相乘正好是100。

生2：不可以，原式中没有加法，下面却出现了加法，上下两个算式结果就不相等了。

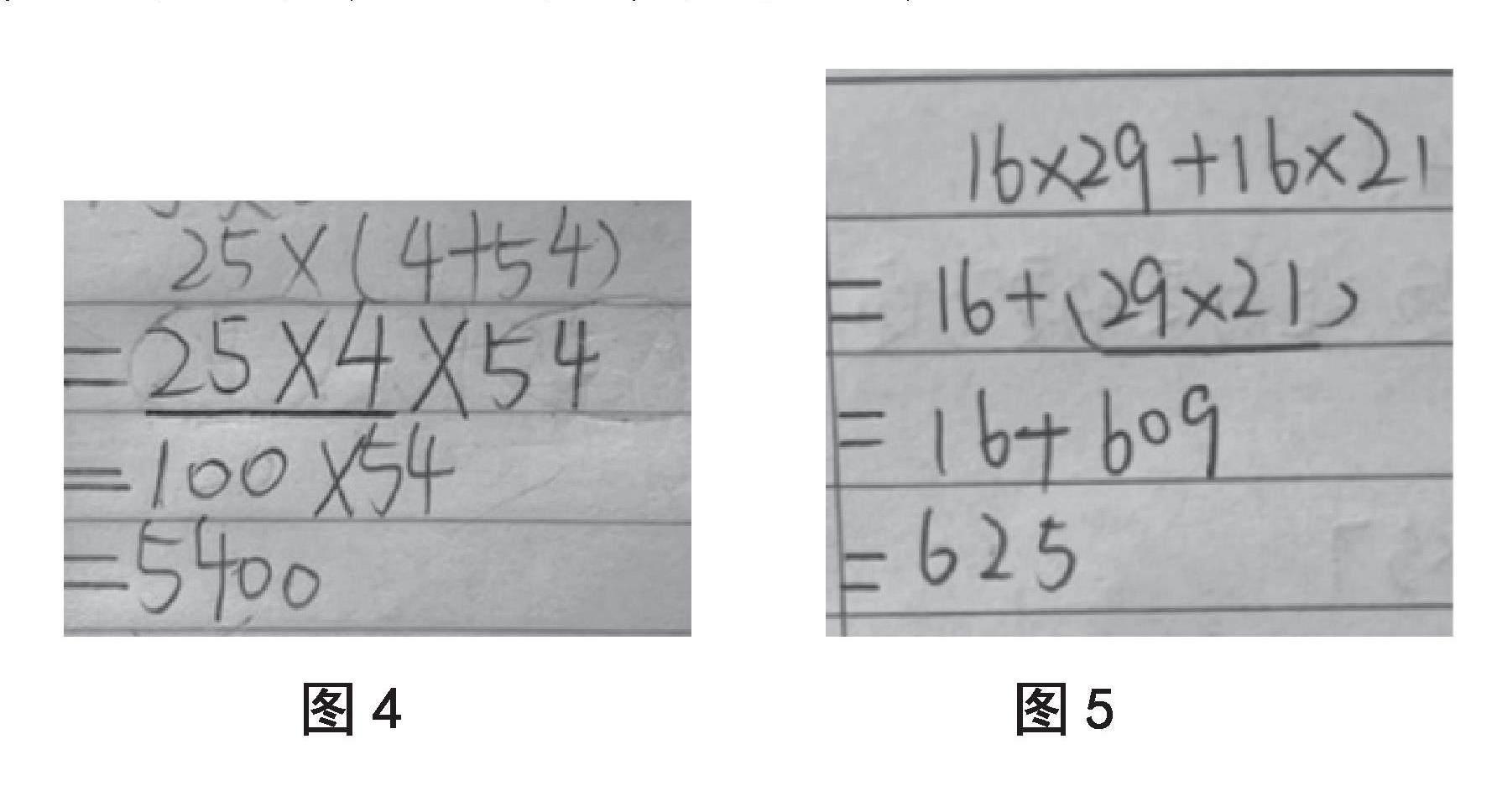
生3：这一题应该使用乘法结合律使25和4凑整。所以原式=25×4×54=100×54=5400。

（同学们纷纷表示赞同）

师：再来看看第三题，它和第二题有什么联系与区别？这一题能简便计算吗？为什么？

生4：算式中的三个数都相同，也都含有括号，就是括号里的符号不同。可以简便计算，因为算式中有25和4，相乘正好是100。

师：黑板上的做法对吗？

生5：不对，使用乘法分配律应该用25去乘括号里的每个数，所以原式=25×4＋25×54。

【设计意图】从上述学生的三个例证中，第一题的形式是标准的乘法分配律“a×c＋b×c=（a＋b）×c”，学生一下子就能找到简便计算的窍门进行计算。第二题和第三题的检测点在于，学生在运用中会不会出现结合律与分配律的混淆。从测试反馈看，果然不出所料，学生对于乘法分配律和乘法结合律的概念认知还不够清晰。这里的第二、第三题有意使用“控制变量”的方法，使算式中数字相同，符号不同。通过这样的横向对比，更加强化了乘法分配律与乘法结合律的区别，以便进行接下来的教学。

师：下面的两题做法对吗？（出示学生作业）比一比，怎样区分乘法结合律和分配律？

生：乘法分配律有乘有加，是二级运算，乘法结合律只有乘法，是同级运算。

师：抓住乘法分配律与结合律的最大不同快速区分，是个好办法。要判断一个算式中是否存在“乘法分配律”，关键要寻找什么？

生（齐说）：相同数。

【设计意图】第二题和第三题“外形”很相似，区别就在于小括号里的符号。班级里近一半的学生将此题做错，究其原因就是对“原型”的认识不够深入。通过这种“同屏对比”的方法，把学生的思维过程展示出来，使学生在对比中发现乘法分配律和乘法结合律的区别。但是在“找”了并“说”了之后，仍需要认识到问题核心：怎样区分乘法结合律和乘法分配律。通过上述两组相对简单却又容易发生混淆题目的横向对比，来引导学生体会“相同因数”是明确乘法分配律原型的关键要素，厘清“乘法结合律”和“乘法分配律”的模型，以期化解学生头脑中的矛盾冲突，更清楚地建立乘法中这两种运算律的模型。

二、纵向对比，体现“乘法分配律”模型的深度

乘法分配律是“运算律”单元的重点，也是“运算律”单元的难点，更是变式较多的知识点。在上述清楚地建立起这两条运算律的表象后，可以对乘法分配律进行更为精细的深化练习，通过分配律各种题型的纵向对比，促使学生突破乘法分配律的变式难点。

出示题组1：口算下面各题，并用乘法分配律解释算理。

23×34×1216×52×48

师：谁来说说你是如何计算“23×3”的？

生：先算“3×3”，再算“十位上的2×3”，合起来就是69。

师：能用乘法分配律解释吗？

生：这样的算法，其实就是把23拆分成20＋3，先算3个3是多少，再算20个3是多少，把两个得数合在一起，就是23×3的结果。

【设计意图】这里的两位数乘一位数的乘法口算，是学生在数学三年级上册就掌握的内容。当时，虽然并没有揭示“乘法分配律”的本质内涵，但在计算中已经充分运用了“乘法分配律”的原理。通过这一题组的计算，可以调动学生已有的学习经验，将新、旧知识进行联结，活跃计算思维，以期实现从“算出结果”向“理解算理”再向“知识建构”的方向跨越发展。同时，即使有的学生不能像教师要求的那样说得贴切、流利，但在这样的思考过程中，也有助于他们跟上接下来的题组练习，辅助其思维向纵深迈进。

出示题组2：用自己的方法计算23×36。

展示下面的学生作业：

师：这里有4位同学的作业，他们用的方法各不相同，你能说说这些方法之间的联系与区别吗？

生1：前两位同学用了竖式计算，后两位同学用了乘法分配律的方法进行计算。

生2：我发现第一个竖式计算和第三个算法其实是一样的。在第一个竖式中，先用个位上的6去乘23，再用十位上的3去乘23，然后把所得结果相加。相当于把36拆分成了30和6，先算6个23是多少，再算30个23是多少，最后直接相加算出36个23是多少。

师：的确，两位数乘两位数的算理是可以用乘法分配律来解释的。

生3：照这样的理解，第二个竖式和第四个算法也是相同的道理。不同的是，刚才是对36进行拆分，这里是对23进行拆分。

师：是啊，不管是把哪个乘数拆分，使用乘法分配律都能使两位数乘两位数的计算变得更加简便。

【设计意图】这是学生在三年级下册就掌握的两位数乘两位数的计算，之所以在这里设计本题，目的是让学生从已有的竖式计算经验中跳出，引导其思考“既然两位数乘一位数可以用乘法分配律解释计算原理，那么，两位数乘两位数是否也可以呢？”通过这一题的练习，学生发现两位数乘两位数，也蕴含着乘法分配律，既可以解释成36个23是多少，也可以解释成23个36是多少，无论拆分哪个乘数，最后都能计算出23×36的结果。进而，学生能够发现，乘法运算都可以用乘法分配律的原理进行解释，而用乘法分配律的思考过程其实就是竖式计算的过程。这样的纵向对比练习，不仅巩固了乘法的算理，又能进一步加深学生对乘法分配律的知识理解。

出示题组3：64×9-14×912×（40-5）

师：这两题，可以简便计算吗？为什么？

生1：不可以。虽然这两题和乘法分配律很像，但是乘法分配律里面是加法，而这里是减法，和乘法分配律不一样。

生2：可以。算式中变了一个符号，但是也可以仿照乘法分配律进行计算。比如第一题，实际上就是用64个9减去14个9，结果是50个9。所以原式=（64-14）×9。第二题也是相同的道理，原式=12×40-12×5。

【设计意图】当学生第一次看到这类算式时，不免会跟“乘加”的算式进行对比，当他发现“乘减”的算式中的减号不符合乘法分配律的模型时，就会给出否定的答案。此时，教师可以直接告诉学生，乘法分配律不仅可以在“乘加”的算式中使用，在“乘减”的算式中也同样适用，再让其尝试计算并进行检验，这样就能达到由“乘加”向“乘减”迁移的目的。

总之，“乘法分配律”的变式较多，不少学生缺乏一些简算的小技能，这也是他们觉得难学的原因之一。因此，在练习中不仅要呈现较为常见的变式题，还应设计一些体现新方法与策略的变式题。在课堂上，将上述3个题组同时抛出，让学生在实际操练、纵向对比提炼中获得简算的新技能，从建立概念结构与原型，到变式练习推进还原，有效提升学生在简算中“灵活应用”的能力，促进其数学思维的发展，充分体现“乘法分配律”模型的深度。

三、交叉对比，拓宽“乘法分配律”思维模型

仅仅把乘法分配律的教学停留在以上层面仍然不够，还应加入思维含量更加丰富的题型，以充实学生对“乘法分配律”的认识，提高他们思维的灵活性。

例1：用简便方法计算下面两题。

35×9876×99

通过上述的两个环节的教学，大部分学生都能想到使用拆分的方法进行计算，例如下图：

通过计算，学生会发现这种算法并没有使计算变得简便，计算量也不小。那么，面对这样类型的题目该如何计算呢？

通过观察“35×98”和刚才的“23×36”，发现“35×98”中的98非常接近整百数100，想到可以从“减法”的角度对本题展开思考：如果用“100-2”代替“98”，是不是可以使计算更加简便呢？通过尝试计算，结果果然如此，计算过程如下图所示：

这样一个交叉对比练习，主要是打开学生思维的灵活性。其实，并不是所有的两位数乘两位数都只能使用“乘加”的方法进行简便计算，有时候使用“乘减”，反而更加简便。如此一来，就可以打破学生的思维定式，培养其多角度思考问题的习惯。

例2：用简便方法计算下面两题。

360×52+480×36999×8+111×28

出示这两题，班级大多数同学都表示，难以进行简便计算，原因是题目中没有相同的乘数，无法使用乘法分配律，同时乘法结合律也没法使用。

此时，教师可以给学生一些提示：

提示1：算式中没有相同的乘数，能否用以前学过的知识使得算式中出现相同的乘数？

提示2：想一想，乘法中有没有什么规律可以实现提示1的目的？

通过这两个提示，有的学生发现：在“360×52+480×

36”中，有两个数比较特殊，即“360和36”。如果把这两个乘数都变成360或者36，那么，本题就能使用乘法分配律进行简便计算。于是，我们想到，应用积的变化规律可以把“360×52”转化成“36×520”，或者把“480×36”转化成“48×360”，这样就能化解计算难点，如下图所示：

同理可得，“999×8+111×28”也可以应用积的变化规律对原式进行等积变形，使其满足乘法分配律的形式，解题过程如下：

【设计意图】例2的教学要点，旨在达成用“相同因数”进行灵活合理地简算的目的。例1与例2变式难度逐级递增，一部分学生无法用已有的认知水平去解决没有相同因数这类变式题。这两道例题一前一后出现，学生一时难以参透其中的奥秘，这时，就需要放慢脚步，找寻困惑之处，然后通过交叉对比的方式，引导学生相互学习与思辨，讨论可行的方法与策略。同时，也要让他们再次尝试与应用，体会“变式”打回“原型”的意义。在加深概念理解的同时，真正获得简算技能，提升运算能力。如此一来，就能拓宽“乘法分配律”思维模型。

通过上面3个层次6个题组的对比教学，笔者获得了以下四点启示：一是结构化的数学教学可以使数学知识更加立体；二是巧妙运用“对比教学法”可以厘清概念，促进知识意义建构；三是从真实的问题出发，可以更适切地帮助学生“拨乱反正”，建立正确的概念；四是螺旋上升的教学方式可以打开学生思维的深度，拓展学生思维的广度。

史宁中教授指出，模型是数学发展所依赖的思想本质之一。因此，理解“乘法分配律”的原型，不能只停留在“外貌”上的认识，更应该在概念本质上去建构，这样才能在应用中体现灵活性。本文从学生常见的错题入手，按照由低到高、由简到难的逻辑顺序，进行同屏的“横向对比”“纵向对比”“交叉对比”，并将这些题目在一堂课上集中呈现。这样的安排，不仅遵循了学生数学学习的规律，还能让其在原有的基础上对乘法分配律的概念加深印象，明白“万变不离其宗”，不管何种题型，不管是否见过，只要抓住“乘法分配律”的本质内涵，就能一通百通。这样的教学，同时也培养了学生思维的深度和宽度，利用螺旋上升的教学方式，把与“乘法分配律”相关的习题进行了分类与整理。经历对典型例题的学习，相信学生已经能够清晰地认识到乘法运算律的概念本质。

［参考文献］

［1］史宁中.基本概念与运算法则[M].北京：高等教育出版社，2013.

［2］曹培英.跨越断层，走出误区：“数学课程标准”核心词的解读与实践研究[M].上海：上海教育出版社，2017.

［3］姜荣富.追问知识意义与核心价值：对运算律的理解维度[J].小学教学，2012（05）.

［4］刘善娜.通性通法：运算律教学的核心价值（二）——“交换律”一课的教学实践[J].教学月刊小学版（数学），2017（Z2）.

［5］任宁，李亦儿.整体推进定序列 多元途径破难点——人教版数学四年级下册“运算定律”单元整体教学思考[J].江西教育，2021（23）.