基于类的余弦距离聚类缺失值填补方法研究

夏婷婷 林康 张潇予 刘海忠

摘 要：【目的】为了解决欧氏距离计算相似性带来的高维度问题，提出了基于类的余弦距离聚类缺失值填补方法。【方法】首先将不完整数据集分为两个不同的组（G1和GIM）；其次通过聚类中心对GIM组中的缺失数据进行预填补；再次利用余弦距离计算相关性；最后选择与G1组中距离最小的数据来填补缺失值。【结果】实验结果表明，该方法在类别和混合数据集上均优于其他插补方法。【结论】该方法显著提高了准确率、召回率、F1-score及插补效果。

关键词：不完整数据；缺失值插补；聚类；余弦距离

中图分类号：TP181；TP311.13  文献标志码：A    文章编号：1003-5168（2024）08-0028-08

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.08.006

A Study of Missing Value Imputation Methods for Class-based Cosine Distance Clustering

XIA Tingting1 LIN Kang2 ZHANG Xiaoyu3 LIU Haizhong1

（1.Lanzhou Jiaotong University， Lanzhou 730070， China; 2.Beijing Normal University， Zhuhai 519087， China;3.School of Social and Behavioral Sciences， City University of Hong Kong， Lanzhou 730070， China）

Abstract： [Purposes] In order to solve the high dimension problem caused by the similarity of Euclidean distance calculation， a class-based cosine distance clustering missing value imputation approach is proposed. [Methods] Firstly， the incomplete data set is divided into two different groups （G1 and GIM）; secondly， the missing data in the GIM group is pre-filled by the clustering center; the cosine distance is used again to calculate the correlation ; finally， the data with the smallest distance from the G1 group is selected to fill the missing values. [Findings] The experimental results show that the proposed method outperforms other imputation methods for both categorical and mixed datasets. [Conclusions] The CBC-IM-COS method significantly improves accuracy， recall and F1-score and imputationperformance.

Keywords： incomplete data; missing value imputation; clustering; cosine distance

0 引言

缺失值的挑战是数据科学中最普遍的问题之一［1］。在医疗数据中尤其如此，由于某些指标难以衡量、数据采集不及时、数据存储不当、医疗信息难以跨平台共享等因素，导致医疗数据中往往存在许多缺失值［2-3］，直接影响疾病诊断、治疗选择、出院评估、预后评估等临床决策。如果不及时处理大量缺失的数据，往往会导致严重的偏差，从而得出错误的结论。因此，有必要对缺失数据进行有效处理，以提高医疗数据的质量和临床决策的准确性。处理缺失数据方法大致可分为2类：删除法和插补法。根据Strike等［4］和Raymond等［5］的研究，当数据集包含非常少量的缺失数据时，如缺失率小于10%或15%，采用删除法删除缺失数据，不会对最终挖掘或分析的结果产生显著影响。但是，当缺失率较大时，该方法则会导致有价值的信息丢失。与删除策略不同，缺失值插入（MVI）是处理不完整数据集问题最常用的解决方法，插补法是从可利用的数据中估计出的数值去替换缺失的值。

目前，缺失值插补法可分为两种类型［6-7］，即基于统计的方法和基于机器学习的方法。基于统计的方法主要有均值、中值、众数以及期望最大化和多重填补技术。Tsai等［8］的研究提出了基于类中心的缺失值插补（CCMVI）方法，该方法通过类中心、标准差、欧式距离来填补缺失值，但是该算法不适用于高缺失率的情况；因此刘莎等［9］改进了类中心、标准差、阈值的计算，并使用灰色关联度计算实例间的相关性，提出了灰色类中心的缺失插补方法，实验结果表明，该方法提供了分类精度和插补效果；朱荣慧等［10］和唐健元等［11］分别介绍了多重填补技术医学研究中和临床研究中的基本思想和步骤；Sefidian等［12］结合灰色关联分析、模糊C均值、互信息、回归模型提出了一种新缺失值填补方法，实验结果表明，提出的方法在RMSE、MAE、决定系数方面优于其他5种填补方法。基于机器学习的方法主要有k近邻（KNN）、支持向量机（SVM）、聚类、随机森林技术。李琳等［13］和白洪涛等［14］证明了随机森林插补具有较好的插补效果；Vazifehdan等［15］使用贝叶斯网络和张量因式分解相结合的方法预测乳腺癌复发的可能性，实验结果表明，该方法能够有效地提高数据质量和预测质量；Batra等［16］提出集成填补模型，并与均值填补、K近邻填补、迭代填补等方法进行比较，对比结果表明所提出的方法在准确性方面优于其他几种缺失值填补方法。

由于现实世界中的许多函数问题都是高维的，为了克服现有的填补技术和应用的距离函数具有高维的问题，Yelipe等［17］提出了基于类的欧式距离聚类缺失值填补（CBC-IM-EUC）方法，较好地解决了这一问题。但该算法的主要缺点是：①随着维度的增加，欧几里得距离的作用就越小；②在计算相似度时，忽略了GIM组中缺失数据的不完整属性值对应的平均向量元素值。邵俊健［18］在不同的大规模高维数据集中，比较了4种不同的距离度量函数，结果表明，余弦距离与欧式距离相比可以得到较好的结果。针对上述问题，本研究提出了基于类的余弦距离聚类缺失值填补（CBC-IM-COS）方法，通过利用余弦距离代替欧式距离来计算实例间的相关性，并且在计算相关性时对GIM组中的缺失数据进行预填补。

1 相关工作

1.1 缺失机制

Little和Rubin［19］将缺失机制分为3种，分别为完全随机缺失（MCAR）、随机缺失（MAR）、非随机缺失（MNAR）。

假设Y为整个数据集的矩阵，该矩阵分解为y0和ym，y0表示数据集Y中没有缺失的数据，ym表示数据集Y中的缺失数据。R是指示变量矩阵，其中0表示数据缺失，1表示数据未缺失，定义见式（1）。

[R=1      yij∈y00      yij∈ym] （1）

①完全随机缺失（MCAR）：表示缺失数据不依赖于其本身和其他未缺失的数据。MCAR的概率定义见式（2）。

[PRym， y0=PR] （2）

②随机缺失（MAR）：表示缺失数据独立于任何缺失值但与其他未缺失的数据有关。在这种机制下，缺失值可以通过观察到的预测变量进行处理［20］。MAR的概率定义见式（3）。

[PRym， y0=PRy0] （3）

③非随机缺失（MNAR）：表示缺失数据依赖于其本身和其他未缺失的数据。MNAR概率定义见式（4）。

[PRym， y0=PRy0， ym] （4）

1.2 缺失值方法

通过介绍和描述用于估算原始不完整数据集的方法，介绍了4种应用的插补技术。

①统计方法包括均值/众数法和多重插补（Multiple imputation）

②基于机器学习的方法包括支持向量机（SVM）和多层感知机（MLP）。

1.2.1 统计方法。统计填补方法包括均值/众数法和多重插补（MI）。

均值/众数法（Mean/Mode method），均值法和众数法分别是数值属性值和分类属性值最简便的插补方法。当数据发生缺失时，均值/众数法是使用未缺失数据的平均值/众数来代替缺失的数据。此方法简单易行，但是忽略了属性之间的依赖关系。

多重插补（Multiple imputation，MI），是由Rubin于20世纪70年代末首次提出，其核心思想认为缺失数据都是随机的［21］。将MI描述为3个步骤。首先，使用适当的模型来创建缺失观测的合理值（通常为5-10个），该模型反映了由缺失数据造成的不确定性。每一组合理的值都可以用来“填充”缺失的值，并创建一个“完整的”数据集；其次，对每个数据集进行分析；最后，将结果进行综合，进而产生最终的预测结果。该方法适用于填补任何类型的数据。MI反映了缺失数据的不确定性，并解决了单一插补［22］的局限性。于是在多重插值方法中，我们选择了链式方程多元归算（multiple imputation by chained equations）（MICE）。

1.2.2 机器学习方法。基于机器学习的估算方法是一个复杂的过程，通常包括创建一个预测模型来估计将替代缺失的值。基于机器学习方法包括支持向量机（SVM）和多层感知机（MLP）。

支持向量机（SVM），是一种有监督学习模型，支持向量机插补缺失数据的原理是先利用不完整数据集中的未缺失数据来训练支持向量机模型，再利用训练好的模型去预测缺失数据。SVM与SVR分别用于离散/类别与连续/数值缺失数据的填补。该方法的优点是无论自变量的维度如何，都能表现出优异的性能。但是，该方法的准确性会随着样本数量的增加而降低。

多层感知机（MLP），是由输入层、隐藏层、输出层组成的前馈神经网络。首先，自变量的值通过输入层进入MLP，并利用隐含层的输入值生成权值的和；其次，通过多个隐藏层重复生成加权和的过程后，利用输出层生成因变量的值并输出；再次，使用反向传播学习算法对构成MLP的神经元进行训练，并在此过程中更新权重；最后，将更新的权重存储在MLP的神经元中，并使用存储的权重定义自变量和因变量之间的非线性关系。

2 总体设计

2.1 整体工作流程

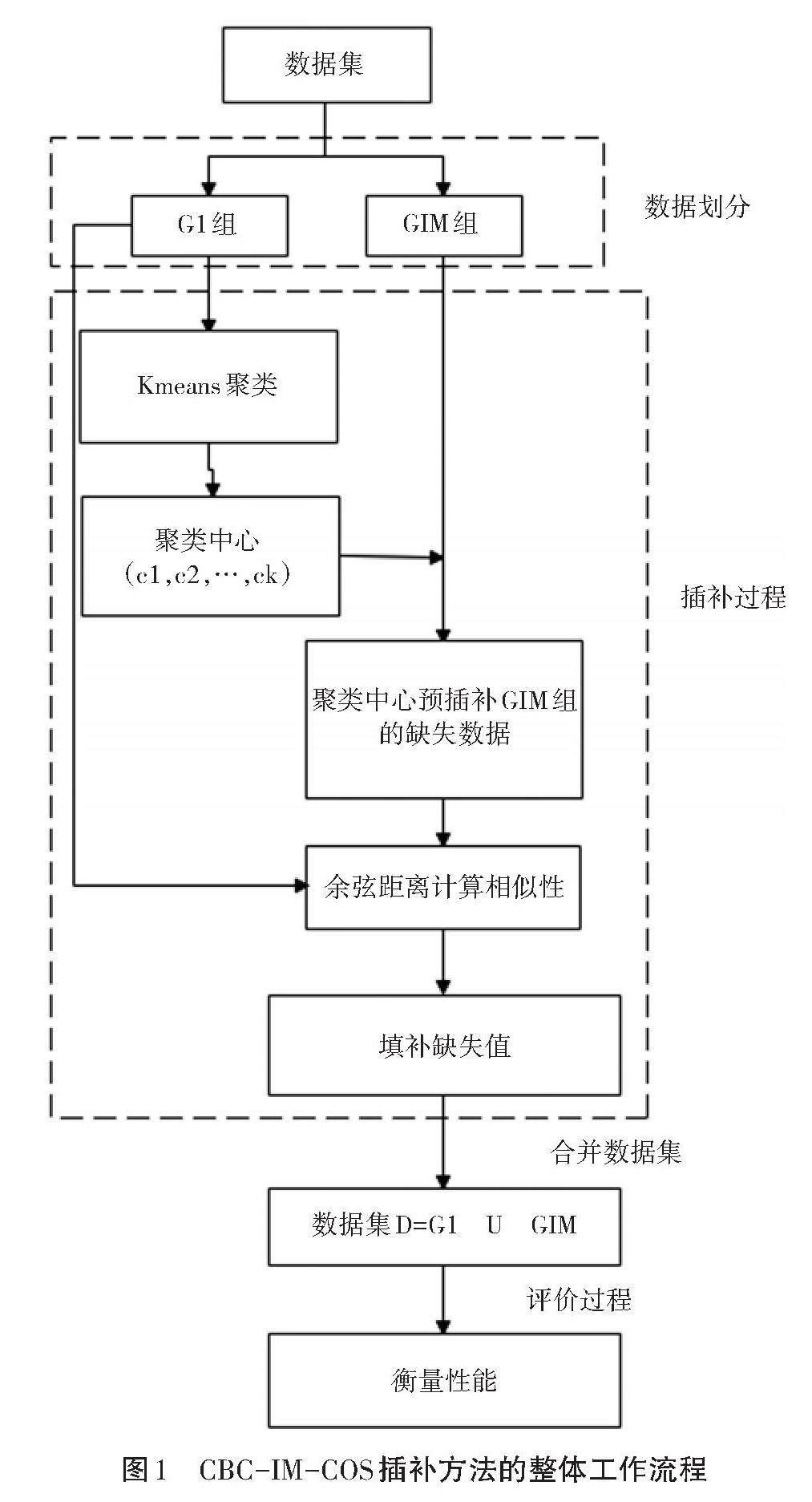
本研究提出的CBC-IM-COS方法的整体工作流程包括4个步骤，如图1所示。

步骤1：数据划分。数据集被划分为2组。G1组（不包含缺失值）和GIM组（包含缺失值）。

步骤2：插补过程。利用CBC-IM-COS方法，进行缺失值插补。

步骤3：合并数据集。把G1组的数据和填补后的GIM组的数据合并在一起，形成一个完整的数据集。

步骤4：评价过程。使用支持向量机分类器，衡量插补的性能。

2.2 CBC-IM-COS方法步骤

首先，将数据分为不包含缺失值（G1）组和包含缺失值（GIM）组，其目的是先考虑G1组的数据；其次，采用Kmeans聚类算法，获得与决策标签数量相等的聚类，并使用所获得的聚类信息去实现降维；再次，通过分析在G1组得到的集群，从而得到每个集群的聚类中心和偏差；然后，利用从G1组得到的聚类中心，对GIM组中的缺失数据进行预填补；最后，使用余弦距离计算缺失的属性值数据和G1组中每个数据之间的距离（或相似度），并选择与G1组中距离最小（或相似度最大）的数据来进行填补。

如果是数字属性，则填写属性值的平均值；如果是名义属性，则选择并替换类似记录的相应属性值。填补完成后，可以得到最终的完整数据集。

3 实验

3.1 数据集

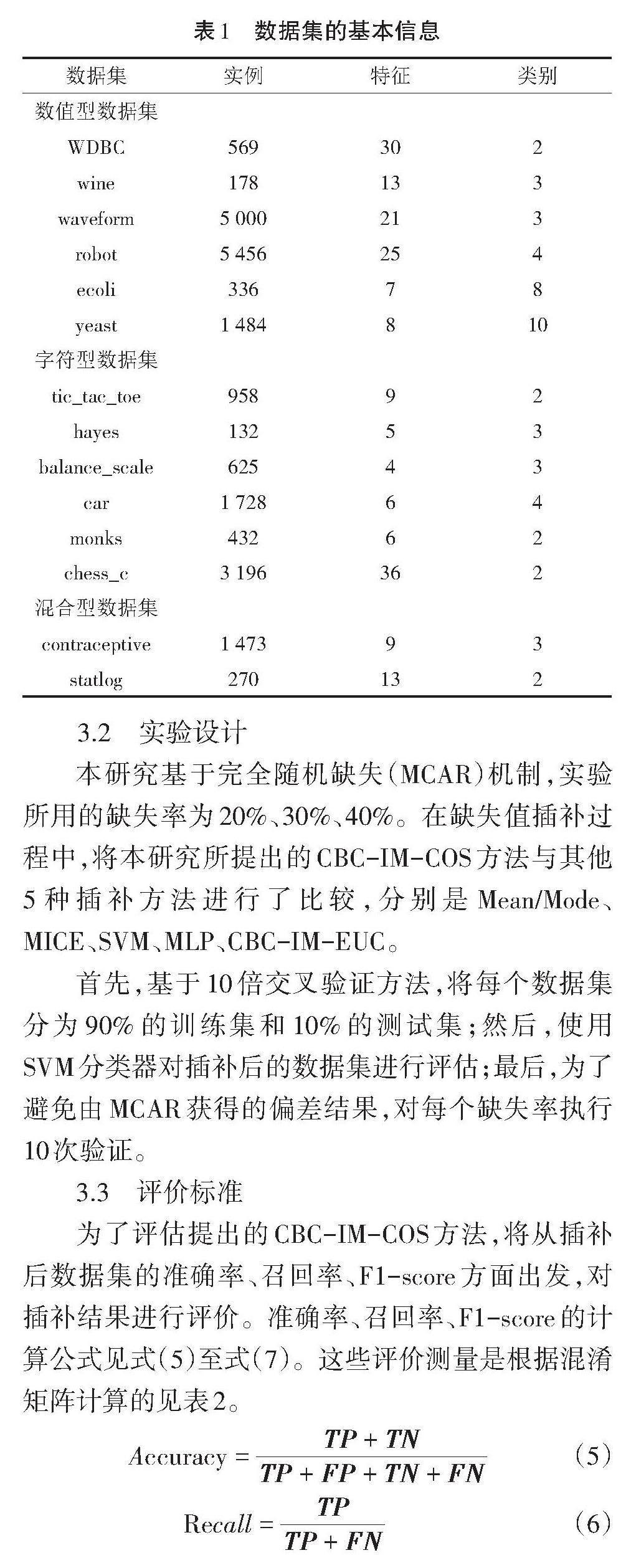
从UCI机器学习库中选择了3种不同类型的数据集，分别为数值型、字符型、混合型数据集。数据样本和属性的数量分别为132到5 000和4到36。数据集的基本信息见表1。

3.2 实验设计

本研究基于完全随机缺失（MCAR）机制，实验所用的缺失率为20%、30%、40%。在缺失值插补过程中，将本研究所提出的CBC-IM-COS方法与其他5种插补方法进行了比较，分别是Mean/Mode、MICE、SVM、MLP、CBC-IM-EUC。

首先，基于10倍交叉验证方法，将每个数据集分为90%的训练集和10%的测试集；然后，使用SVM分类器对插补后的数据集进行评估；最后，为了避免由MCAR获得的偏差结果，对每个缺失率执行10次验证。

3.3 评价标准

为了评估提出的CBC-IM-COS方法，将从插补后数据集的准确率、召回率、F1-score方面出发，对插补结果进行评价。准确率、召回率、F1-score的计算公式见式（5）至式（7）。这些评价测量是根据混淆矩阵计算的见表2。

[Accuracy=TP+TNTP+FP+TN+FN] （5）

[Recall=TPTP+FN] （6）

[F1-score=TPTP+FP+FN2] （7）

3.4 实验结果

3.4.1 数值型数据集实验结果及分析。在数值型数据集上不同的MVI方法对不同缺失率下SVM的平均准确率、召回率、F1-score见表3。由表3可知，平均来说，CBC-IM-COS方法在召回率上表现最好，在准确率和F1-score上取得了次最优的结果。并且，CBC-IM-COS方法相较于CBC-IM-EUC方法的准确率和召回率分别增加了0.26%和0.13%。

不同的MVI方法在数值型数据集上的不同缺失率下的准确率、召回率、F1-score如图2所示。由图2可知，当缺失率为20%时，CBC-IM-COS方法在准确率方面略低于Mice；当缺失率为20%和40%时，CBC-IM-COS方法在召回率方面优于其他填补方法；当缺失率为20%，CBC-IM-COS方法在F1-score表现最好。

3.4.2 字符型数据集实验结果及分析。在字符型数据集上不同MVI方法对不同缺失率下SVM的平均准确率、召回率、F1-score结果见表4。由表4可知，在F1-score上，众数法的效果最好，但是，由于众数法没有考虑到数据之间的相关性，所以认为CBC-IM-COS方法较好。并且，CBC-IM-COS方法相较于CBC-IM-EUC方法的准确率、召回率、F1-score分别增加了0.25%、0.22%、0.16%。

不同MVI方法在字符型数据集上的不同缺失率下的准确率、召回率、F1-score如图3所示。由图3可知，对于不同的MVI方法，随着缺失率的增加，准确率、召回率、F1-score逐渐下降。当缺失率为20%和30%时，众数法是最佳选择；当缺失率为40%时，CBC-IM-COS方法表现最好。

3.4.3 混合型数据集实验结果及分析。在混合型数据集上不同MVI方法对不同缺失率下SVM的平均准确率、召回率、F1-score结果见表5。由表5可知，CBC-IM-COS方法与MLP取得了相同的Accuracy，在召回率和F1-score上，CBC-IM-COS方法表现最好；在Recall上CBC-IM-COS方法取得了次最优的结果。并且，CBC-IM-COS方法相较于CBC-IM-EUC方法的准确率、召回率、F1-score分别增加了0.27%、0.24%、0.27%。

不同MVI方法在混合型数据集上的不同缺失率下的准确率、召回率、F1-score如图4所示。由图4可知，对于不同的MVI方法，随着缺失率的增加，准确率、召回率、F1-score先下降再上升。当缺失率为20%和40%时，Mice优于其他的填补方法；当缺失率为30%时，CBC-IM-COS方法表现最好。

4 结论

本研究针对高维数据的缺失值问题，提出了基于类的余弦距离聚类缺失值填补（CBC-IM-COS）方法，使用了3种不同类型的数据集，即数值型、字符型、混合型数据集，将CBC-IM-COS方法与5种常用方法（Mean/Mode、MICE、SVM、MLP及CBC-IM-EUC方法）进行对比。实验结果表明，对于数值型数据集，CBC-IM-COS方法在召回率上取得了较好的结果；对于分类型数据集，CBC-IM-COS方法在准确率、召回率、F1-score上均优于其他填补方法；对于混合型数据集，CBC-IM-COS方法在准确率和F1-score上取得了较好的结果。并且，对于字符型和混合型数据集，CBC-IM-COS方法相较于CBC-IM-EUC均能在一定程度上提高准确率、召回率、F1-score。除此之外，对于字符型和混合型数据集，CBC-IM-COS方法分别在缺失率为30%和40%时获得最优的结果。

本研究仅基于MCAR机制对缺失数据进行模拟，未考虑其他2种（MAR和MNAR）缺失机制，并且仅使用了SVM分类器衡量插补效果，在未来研究中可使用多种分类器进行综合比较。

参考文献：

［1］ZHANG Z H.Missing data imputation：focusing on single imputation［J］. Ann Transl Med， 2016，4（1）：9.

［2］STONKO D P，BETZOLD R D，ABDOU H，et al.In-hospital outcomes in autogenous vein versus synthetic graft interposition for traumatic arterial injury：a propensity-matched cohort from proovit［J］. Journal of Vascular Surgery，2022，75（5）：1787-1788.

［3］PURRUCKER J C，HAAS K，RIZOS T，et al.Early clinical and radiological course，management，and outcome of intracerebral hemorrhage related to new oral anticoagulants［J］. JAMA Neurology，2016，73（2）：169-177.

［4］STRIKE K，EL E K，MADHAVJI N. Software cost estimation with incomplete data［J］. IEEE Transactions on Software Engineering，2001，27（10）：890-908.

［5］RAYMOND M R，ROBERTS D M.A comparison of methods for treating incomplete data in selection research［J］.Educational and Psychological Measurement，1987，47（1）：13-26.

［6］AITTOKALLIO T.Dealing with missing values in large-scale studies：microarray data imputation and beyond［J］.Briefings in Bioinformatics，2010，11（2）：253-264.

［7］GARCIA-LAENCINA P J， SANCHO-GOMEZ J L，Figueiras-Vidal A R.Pattern classification with missing data：a review［J］. Neural Computing and Applications，2010，19（2）：263-282.

［8］TSAI C F，LI M L，LIN W C. A class center based approach for missing value imputation［J］. Knowledge-Based Systems，2018，151：124-135.

［9］刘莎，杨有龙.基于灰色关联分析的类中心缺失值填补方法［J］.四川大学学报（自然科学版），2020，57（5）：871-878.

［10］朱荣慧，许金芳，王睿，等.多重填补技术在医学研究缺失值处理中的应用及发展［J］.中国卫生统计，2022，39（2）：293-295，298.

［11］唐健元，杨志敏，杨进波，等.临床研究中缺失值的类型和处理方法研究［J］.中国卫生统计，2011，28（3）：338-341，343.

［12］SEFIDIAN A M，DANESHPOUR N. Missing value imputation using a novel grey based fuzzy c-means，mutual information based feature selection，and regression model［J］. Expert Systems with Applications，2019，115：68-94.

［13］李琳，杨红梅，杨日东，等.基于临床数据集的缺失值处理方法比较［J］.中国数字医学，2018，13（4）：8-10，80.

［14］白洪涛，栾雪，何丽莉，等.基于缺失森林的医疗大数据缺失值插补［J］.吉林大学学报（信息科学版），2022，40（4）：616-620.

［15］VAZIFEHDAN M，MOATTAR M H，JALALI M.A hybridbayesian network and tensor factorization approach for missing value imputation to improve breast cancer recurrence prediction［J］. Journal of King Saud University-Computer and Information Sciences，2019，31（2）：175-184.

［16］BATRA S，KHURANA R，KHAN M Z，et al.A pragmatic ensemble strategy for missing values imputation in health records［J］. Entropy，2022，24（4）：533.

［17］YELIPE U R，PORIKA S，GOLLA M.An efficient approach for imputation and classification of medical data values using class-based clustering of medical records［J］. Computers and Electrical Engineering，2018，66：487-504.

［18］邵俊健.高维数据的聚类算法及其距离度量的研究［D］.无锡：江南大学，2019.

［19］LITTLE R J A，RUBIN D B. Statistical Analysis with Missing Data［M］. John Wiley and Sons，2019.

［20］GOMEZ-CARRACEDO M P，ANDRADE J M，LOPEZ-MAHIA P，et al.A practical comparison of single and multiple imputation methods to handle complex missing data in air quality datasets［J］. Chemometrics and Intelligent Laboratory Systems，2014，134：23-33.

［21］RUBIN D B. Multiple imputation after 18+ years［J］. Journal of the American statistical Association，1996，91（434）：473-489.

［22］UUSITALO L，LEHIKOINEN A，HELLE I，et al.An overview of methods to evaluate uncertainty of deterministic models in decision support［J］. Environmental Modelling and Software，2015，63：24-31.

收稿日期：2023-10-18

作者简介：夏婷婷（1997—），女，硕士生，研究方向：缺失值插补。

通信作者：刘海忠（1969—），男，硕士，研究方向：数据科学与时空预测决策。