金属材料表面发射率测量装置的设计与应用
2024-06-21黄锦冬史玉豪陈孟涛戴彭宇吴传书梁博李圣慧张航
黄锦冬 史玉豪 陈孟涛 戴彭宇 吴传书 梁博 李圣慧 张航


摘 要:【目的】针对测量管壳式热交换器的管束表面发射率精度低、成本高的问题,设计了测量金属材料表面发射率的装置,提出测量金属材料表面发射率的方法。【方法】该装置结合温度平滑算法后,可以对设备全工作状态时被测材料表面发射率进行测量。【结果】使用该方法对块状钢材样品在200~500 ℃温度区间内进行测试,结果表明,标准算法下的温度仍然存在波动,且会造成发射率的振荡。而采用优化算法对于噪声和发射率有明显的平滑作用,即使面对外部环境扰动也有足够的抗性。【结论】研究结果可为相关设备炉内温度的精确测量提供参考。
关键词:表面发射率;碳钢;辐射传热;连续测量
中图分类号:TG806 文献标志码:A 文章编号:1003-5168(2024)08-0044-06
DOI:10.19968/j.cnki.hnkj.1003-5168.2024.08.009
Design and Application of Surface Emissivity Measuring Device for
Metallic Materials
HUANG Jindong1 SHI Yuhao1 CHEN Mengtao1 DAI Pengyu1 WU Chuanshu1
LIANG Bo1 LI Shenghui1 ZHANG Hang1,2
(1.School of Aviation and Transportation, Jiangsu College of Engineering and Technology, Nantong 226006, China; 2.Liupanshui Shuangyuan Aluminum Industry Limited, Liupanshui 553022, China)
Abstract: [Purposes] In response to the problem of low accuracy and high cost of measuring the surface emissivity of tube bundles in shell-and-tube heat exchangers, this paper designed a device for measuring the surface emissivity of metal materials and proposed a method for measuring the surface emissivity of metal materials. [Methods] The device combined with a temperature smoothing algorithm can provide measurement of the surface emissivity of the material under test when the equipment is in full operating condition. [Findings] The method was used to test lumped steel samples in the temperature range of 200~500 ℃, and the results show that the temperature under the standard algorithm still fluctuates and causes the emissivity to oscillate. The optimization algorithm has a significant smoothing effect on the noise and emissivity, and is sufficiently resistant even in the face of external environmental perturbations. [Conclusions] The results of the study can provide a reference for the accurate measurement of the temperature in the furnace.
Keywords: surface emissivity; carbon steel; radiative heat transfer; continuous measurement
0 引言
表面发射率是表征物质表面辐射能力的物理量。发射率越大,物体表面的热辐射越强烈,热量传递的速度也越快,因此,表面发射率是一项重要的热物性参数,在很多领域发挥着重要的作用。例如,在红外遥感技术中,通过测量物体表面的发射率可以推断其温度和热辐射性质[1-2];在国防军事领域,发射率被应用于雷达和红外探测器中,可以用来进行目标检测和跟踪[3-4],以及对隐身涂层进行性能评估[5];在工业生产领域,发射率被应用于辐射测温中,可以实时非接触式探测工作现场温度变化[6-7]。因此,发射率的测定具有重要意义。
稳态量热法是一种常用的发射率测量方法。该方法测量精度可达2%,测温范围为-50~1 000 ℃[8]。但是,该方法只能测量全波长半球发射率,不能测量光谱或定向发射率[9]。瞬态量热法采用瞬态加热技术(如激光、电流等),使试样温度急剧升高,通过测量试样温度、加热功率等参数,再结合辅助设备测量物体的发射率。其优点为设备相对简单、测量速度快、测温上限高(4 000 ℃以上)、精度高,缺点是只能测量导体材料[10]。红外测温仪法测量范围广、速度快,不需要接触样品,因此测量精度高,但是这种方法的成本较高[11]。
此外,还有一些其他方法可以用来辅助测量发射率,如使用热像仪进行温度测量和校准等[12]。上述这些方法和设备可高精度测量大温度范围的发射率,但是在被测设备连续运行的情况下无法进行测量,只能停机,这会增加运营维护成本和时间成本。本研究基于辐射模型,设计了一种可连续测量金属材料温度变化下发射率的装置和方法。
1 辐射模型
将室温下的球形金属物体,在初始时刻放入一个加热的球形空腔中,如图1所示。金属球的初始温度设为T1,空腔初始温度设为T2。T1和T2都是时间t的函数。
现对两个同心球面之间的辐射传热进行计算。内球面的平均温度设为T1,外球面的平均温度设为T2。内球面的表面积和发射率分别设为A1和ε1,外球面的表面积和发射率分别设为A2和ε2。假设球面是漫反射灰体[13],内球面的净辐射热流的表达式[14]见式(1)。
[Qrad=AσT42-T411ε2T2+A1A21ε2T2-1] (1)
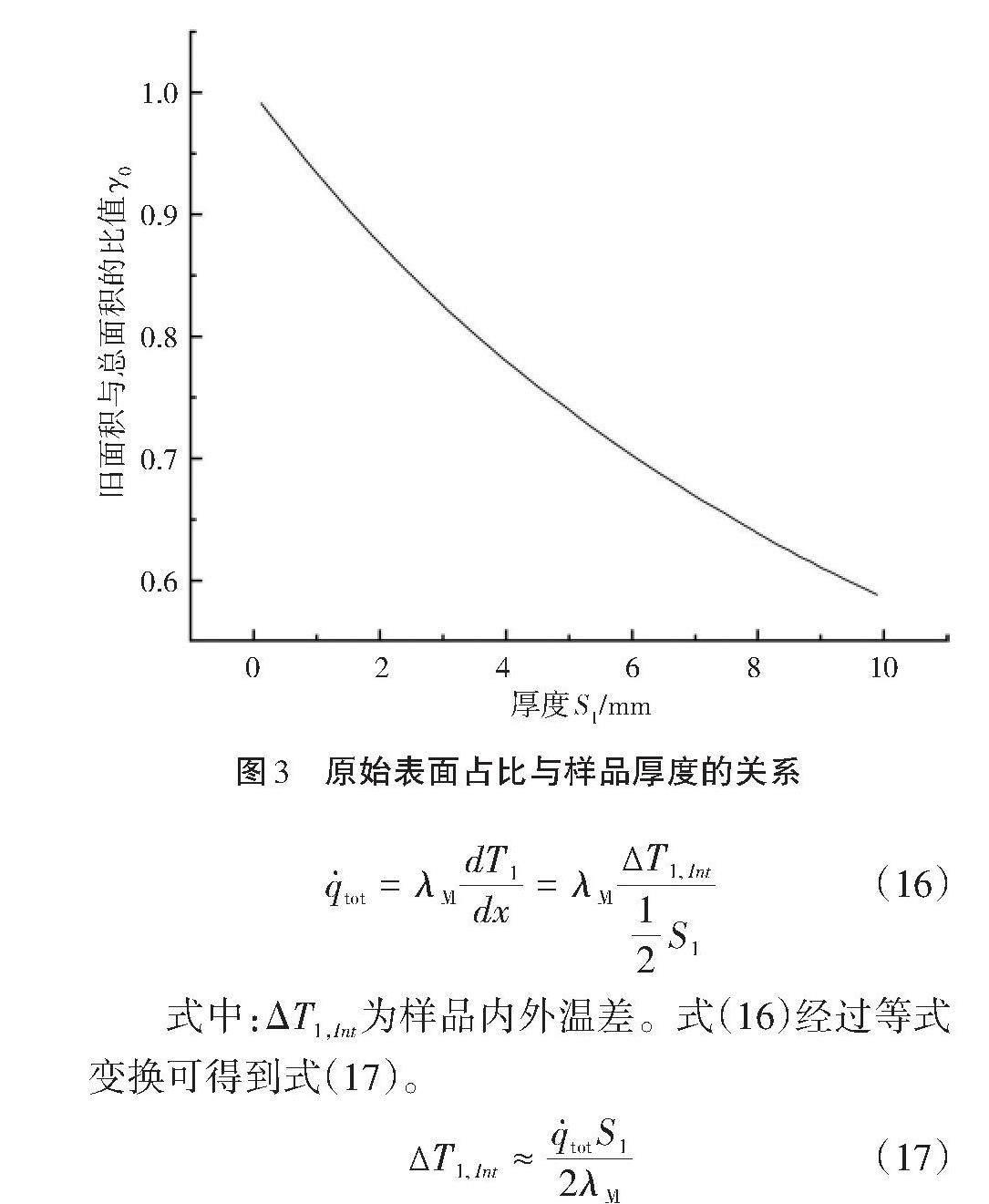
式中:σ为Stefan-Boltzmann常数,取5.67×10-8 W/(m2K4);Qrad正值表示内球面为接收热量(T2>T1),而Qrad负值表示内球面为输出热量(T2 [Qrad=ε1T1AσT42-T41] (2) 即净辐射热流与外球面的发射率无关。在任一时刻,球体都处于能量平衡状态,能量平衡方程可以写成式(3)。 [m1cp1dT1dt=iQi] (3) 式中:m1为物体的质量;cp1为物质的比热;t为时间;Qi为物体与环境之间的换热量,包括辐射热 Qrad和对流热Qconv。因此,式(3)可以变换成式(4)。 [m1cp1dT1dt=QRad+QConv=ε1T1A1σT42-T41+ hconvA1T2-T1] (4) 由此发射率ε1(T1)的表达式可变换成式(5)。 [ε1T1=m1cp1dT1dt-hconvA1T2-T1A1σT42-T41] (5) 式中:m1、σ、A1和cp1已知。在试验过程中记录T1(t)和T2(t)后,hconv通过式(6)至式(10)计算得到,从而确定材料的发射率ε1(T1)。流体与流体中球体之间的自然对流传热方程[15]见式(6)。 [Nu=1.414+0.387Ra1/61+0.492Pr9/168/272] (6) 式中:Nu为Nusselt数;Ra为Rayleigh数;Pr为Prandtl数。Nu的定义见式(7)。 [Nu=hConvLλA] (7) 式中:λA为流体的热导率。Ra的定义见式(8)。 [Ra=Gr?Pr] (8) 式中:Gr为Grashof数,Gr的定义见式(9)。 [Gr=gL31v2AT2-T1T2] (9) 式中:g是万有引力常数(9.81 m/s2);νA是流体的运动黏度。Pr的定义见式(10)。 [Pr=μACpAλA] (10) 式中:μA为动力黏度;CpA为等压比热容。 2 试验方案 2.1 加热炉设计 从实现炉内均匀热辐射场的角度来看,球形炉腔较为合适。但球形炉的成本高,不适合该方法和装置的推广,所以该试验采用更为广泛的平底炉。 炉膛的最小尺寸由辐射传热公式(1)中的假设条件确定,即A2?A1。假设金属样品的长宽为50 mm×20 mm,表面积为1 000 mm2,炉膛表面积约为100 000 mm2,则炉膛左右侧面长宽约为500 mm×200 mm。 为了在某温度范围内获得更准确的材料发射率,样品必须加热到500 ℃以上[16]。为了确保辐射传热是主要的换热方式,炉温应该设置得足够高。否则,发射率测量过程中的任何噪声都对结果非常敏感[17]。因此,必须要求符合式(11)。 [QRadQConv?1] (11) 将式(11)代入式(2)和对流传热的表达式,则得到式(12)。 [QRadQConv=ε1A1σT42-T41hConvT2-T1?1] (12) 当已知ε1、hConv、T1的范围时,式(12)可以用来估算炉温T2的设置范围。通过计算分析,最终炉温选择200~500 ℃。 2.2 样品制备 样品是各种类型的钢材或其他金属材料,形状可以是片材、板材和型材。在该试验中,样品的形状如图2所示。 该试验的样品是从一个大平板上切出来的,那么就存在新旧表面不同的发射率。因此,在制作样品时,尽量使其中旧表面的面积足够大,以确保发射率的精确度。 样品的总面积见式(13)。 [A1, tot=2W1L1+2W1S1+2L1S1] (13) 而旧表面的面积见式(14)。 [A1, o=2W1L1] (14) 因此,测试样品的原始表面积与总表面积的比见(15)。 [γo=A1, oA1, tot=2W1L12W1L1+2W1S1+2L1S1=11+S1L1 +S1W1] (15) 当L1、W1已知的情况下,γo是厚度S1的函数。可以看出,随着样品厚度的增加,γo的值迅速下降。当L1=50 mm、W1=20 mm时,γo与S1的函数关系如图3所示。 此外,样品厚度还受能量平衡方程假设条件的制约,即在试验过程中样品内部温度保持均匀。实际上,由于从样品表面到内部的热传导需要一段时间,因此内部温度并不均匀。当样品的长度和宽度远远大于厚度时,传热问题本质上是一维的。设qtot为样品表面的总热通量,λM为样品材料的热导率,则样品表面的导热可由式(16)算出。 [qtot=λMdT1dx=λM?T1, Int12S1] (16) 式中:ΔT1,Int为样品内外温差。式(16)经过等式变换可得到式(17)。 [?T1, Int≈qtotS12λM] (17) 由式(17)可以看出,样品的内外温差与样品厚度的关系。当炉温达到500 ℃时,qtot约为26 kW/m2,而不锈钢的λM≈20 W/(m·k)。因此,对于厚度为5 mm的样品,ΔT1,Int约为3.3 K,这个温差是可以接受的。结合经验可知,样品的厚度应该至少为2 mm[18]。 样品长度L1的选取需要根据炉内空气与样品之间的对流传热来确定。式(6)至式(10)经过合并变换后可得到样品长度L1与hConv的关系式。空气和空气中的垂直板之间自然对流的对流传热系数如图4所示。由图4可知,长度越小,样品的对流传热系数越高。为了确保辐射传热的主导地位,需要尽量减小对流换热的占比,所以样品的长度不应小于50 mm。 综上所述,样品的尺寸建议厚度为2~5 mm、长度为50 mm、宽度约为20 mm的扁平块状材料。 3 试验过程 3.1 设备与样品 马弗炉采用上下结构,上层为工作区,下层为控制区,如图5所示。上层采用双层陶瓷,四面加热,右侧配有热电偶插孔。下层配备数字式PID控制器,可调节升温曲线,温度上限为1 000 ℃。马弗炉的炉膛尺寸:长400 mm、宽200 mm、高180 mm、表面积0.376 m2。 样品制备:在材料厚度方向上切一个3 mm深的矩形槽,如图2所示。将热电偶插入槽中,并用螺旋压力机将热电偶紧紧压在槽的两侧。将样品悬挂在炉膛内的铁质吊钩上,热电偶的导线穿过马弗炉侧面小孔与温度采集器相连。 3.2 炉温测量 炉内空气的温度通过K型热电偶进行测量,3个热电偶被固定在支架上,高度分别为20 mm,70 mm和120 mm,如图5所示。导线的外漆在燃烧过程(温度超过400 ℃)中,热电偶产生的信号剧烈振荡,无法获得有用数据。但是,热电偶没有外漆仍可以稳定工作,因此,试验中使用的热电偶都是预先燃烧过的。 炉膛内空气的温度分布如图6所示。由图6可以看出,在炉门打开(t=120 s)后的20 s,炉温存在较大波动。 3.3 数据记录与处理 温度数据的采集与记录选用的控制核心是STM32单片机。为了提高精度和稳定性,选用热电偶数字转换器MAX6675对信号进行处理。STM32单片机的内核采用ARM公司的Cortex-M3架构,最高工作频率72 Hz,存储空间256 k,内存48 k,通信接口丰富。在正常工作时,热电偶的模拟信号经过冷端补偿、线性化、放大后送入单片机。MAX6675芯片可以有效解决热电偶信号传输过程中的问题[19]。MAX6675与单片机通过3线串口进行通信。单片机每间隔1 s记录样品(1个通道)和炉膛(3个通道)的温度,并按串行通信协议存储为TXT文件。 一般起始温度选择为过渡期结束时的温度。在该试验中,时间起点为达到设定值±20 ℃以内的任意时刻。选择时间终点的原则为样品温度变化速率达到dT1/dt项的相对不确定度上限。因此,时间终点为样品温度比炉温设定值低100 ℃的任意时刻。 在炉温到达设定温度15 min后打开炉门,将样品及其支撑架放入,关闭炉门。当样品的温度开始接近炉温时,再次打开炉门,将样品和支撑架从炉中取出。最后,终止记录数据。当炉门打开时存在低频噪声的污染,因此采用以下方法进行额外的平滑处理。 样品温度dT1/dt的时间导数按标准算法处理:首先,将每个时间点及其前后各四个单位时间的平均温度作为当前时间的样品温度。然后,在ti时刻的样品温度导数按式(18)计算。 [dT1dt=T1, i+1-T1, i-12?t] (18) 利用式(6)至式(10)计算样品与炉膛内空气之间的对流传热系数。炉内空气的热力学参数是在炉膛和样品的平均温度下取得的。 4 结果与分析 样品的升温曲线及发射率如图7所示。样品和空气的温度,如图7(a)所示。由图7(a)可知,样品在t=120 s时温度发生急剧下降,受热电偶采样方式的影响出现温度振荡。在炉门关闭后,样品温度测量受热电偶性能的影响出现轻微浮动。使用标准算法对噪声污染的数据进行分析得到发射率的温度在达到400 ℃后,出现振荡,说明常规方法对噪声的处理不能满足要求。 优化算法后,样品温度为样品表面温度与炉温的平均值。炉温的采样点是三个不同高度、三个不同深度的空间点。样品温度dT1/dt的时间导数按以下方式计算:首先,每个时间点的温度是当前温度与前后各4个点的温度变化率的平均值的乘积,再加上当前温度作为当前时间的样品温度;然后,在ti时刻的样品温度导数由式(18)算出。 从处理结果可以看出,样品进出炉时的温度变化过程更加缓慢。优化算法的结果比标准算法得到的结果更平滑,如图7(b)所示。 5 结论 金属表面的发射率是工业生产设备中的重要参数,因此发射率的精确测定可以提高生产效率。本研究设计开发了一种用于测量金属材料表面发射率的装置及方法,可以连续测量设备在线工作时金属材料表面的发射率。通过试验得到以下结论。 ①样品温度数据受热电偶抗干扰性能影响,但是可以通过算法进行反馈补偿。在炉膛的封闭体系内,样品的温度出现浮动。使用标准算法可以对噪声数据进行一定优化,但是仍然存在波动。而且,这种波动对于发射率的振荡没有抑制作用。采用优化算法对于噪声和发射率有明显的平滑作用。 ②当炉门开启时,环境扰动也会导致温度数据呈现不稳定波动,但是优化算法在温度区间内对于这类扰动有足够的抗性。 参考文献: [1]刘波,李海洋,刘夷平,等.材料表面发射率的影响及其测量技术研究进展[J].工业计量,2018,28(6):90-94. [2]刘波,郑伟,李海洋.材料表面发射率测量技术研究进展[J].红外技术,2018,40(8):725-732. [3]石东平,吴超,李孜军,等.红外热像技术在安全领域的研究进展[J].红外技术,2015,37(6):528-535. [4]刘占一,许婷,张魏静,等.热防护材料表面发射率测试研究[J].火箭推进,2019,45(4):79-84,90. [5]谈珍,李博文.低发射率红外隐身涂层的制备[J].现代涂料与涂装,2016,19(11):13-16. [6]王聪,代蓓蓓,于佳玉,等.太阳能光电、光热转换材料的研究现状与进展[J].硅酸盐学报,2017,45(11):1555-1568. [7]张衍国,张颖,杨潇潇.高炉熔渣颗粒热物性参数的瞬间测量[J].清华大学学报(自然科学版),2020,60(3):248-253. [8]林芳,胡进坤,徐海涛,等.不同表面粗糙度金属的辐射发射率实验设计[J].实验技术与管理,2018,35(12):43-47,61. [9]胡轶嵩,姜葳,罗发,等.高温氧化对304不锈钢红外发射率影响研究[J].西北工业大学学报,2020,38(1):225-229. [10]冯驰,刘思源.涡轮叶片发射率测量[J].哈尔滨商业大学学报(自然科学版),2020,36(5):576-581. [11]李文军,徐永达,郑永军.红外热像仪与表面热电偶测量发射率的匹配法[J].中国测试,2017,43(6):12-15. [12]元月,宇慧平,秦飞,等.热像仪对QFN封装表面发射率环境透射率的标定[J].红外与激光工程,2017,46(9):216-220. [13]刘硕,朱希安,王占刚,等.三维灰体辐射传递系数蒙特卡罗的GPU计算[J].计算机应用研究,2019,36(11):3357-3360. [14]王怡,王宇琨,孟晓静.高温热源工业建筑室内辐射热在各壁面分布研究[J].西安建筑科技大学学报(自然科学版),2020,52(2):302-308. [15]PATEL P A, BHATNAGAR D, KUMAR S R, et al. Numerical study on turbulent natural convection and radiation heat transfer of nanofluids in a differentially heated square enclosure[J]. Journal of Thermal Analysis and Calorimetry,2020,147(1):675-684. [16]王煜伟,张禹,任建新,等.过热器管壁温度红外在线测量系统研究[J].锅炉技术,2020,51(5):5-10. [17]刘光昱,宦克为,安保林,等.基于积分球反射法的面辐射源发射率分布测量研究[J].计量学报,2023,44(4):503-507. [18]周玉雪,任培旗,张文杰,等.填料近表层分布对红外隐身涂层发射率的影响[J].节能技术,2023,41(2):99-104,129. [19]程智,张文昌.基于无线传感网络技术的热解炉温度测量节点设计[J].医疗卫生装备,2009,30(9):20-23. 收稿日期:2024-01-09 基金项目:2023年江苏省职业院校学生创新创业培育计划项目(G-2023-0364);江苏省高职院校青年教师企业实践培训项目(2023QYSJ021);江苏工程职业技术学院自然科学研究基金项目(GYKY/2022/6、GYKY/2022/3);江苏省高等学校基础科学(自然科学)研究重大项目(23KJA460004);江苏省高等学校基础科学(自然科学)研究面上项目(22KJD510002);南通市社会民生科技计划项目(MSZ2022168)。 作者简介:黄锦冬(2003—),男,本科生,研究方向:热力设备的智能检测。 通信作者:张航(1987—),男,博士,讲师,研究方向:热力设备的故障检测。
