四自由度串联嫁接机器人架构约束模块识别可视化方法
2024-06-17张国渊王豪李栋廉佳汝闫超
张国渊 王豪 李栋 廉佳汝 闫超
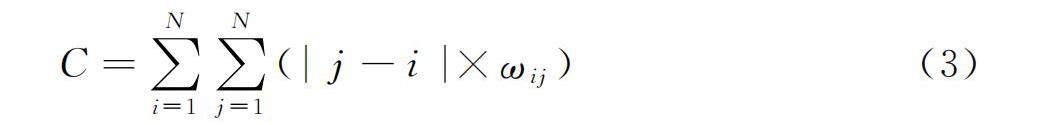
摘要:为实现育苗嫁接的智能化与高效化,一类四自由度串联嫁接机器人的新结构被提出;针对其机械结构、时序控制、联动运行等复杂性,发展该类机器人架构约束下的模块识别可视化方法及设计流程。首先,构建考虑特定架构约束下机器人的设计结构矩阵(DSM),并采用大型社区快速展开算法(LOUVAIN算法)实现对机器人架构模块的预划分;其次,采用改进遗传算法(AGA)对DSM进行聚类,获得多组高模块度的划分结果,由此形成成组可能性矩阵(GLM),并将其对角化得到对角GLM(DGLM);最后,提出针对DGLM的可视化策略并完成着色处理,实现对最优模块划分方案的辨识。结果显示:四自由度串联嫁接机器人可分解为较独立的7大模块,模块度可达0.782。
关键词:嫁接机器人;模块化设计;架构约束;遗传算法
中图分类号:S220; TH112
文献标识码:A
文章编号:2095-5553 (2024) 06-0191-10
收稿日期:2023年3月8日
修回日期:2023年3月30日
*基金项目:陕西省重点研发计划项目(2022GY—314)
第一作者:张国渊,男,1979年生,甘肃靖远人,博士,教授;研究方向为摩擦学、旋转机械动力学。E-mail: guoyuanzhang@xidian.edu.cn
Visualization method for architectural constraint module indentification
of four-degree-of-freedom serial grafting robot
Zhang Guoyuan, Wang Hao, Li Dong, Lian Jiaru, Yan Chao
(School of Mechano-Electronic Engineering, Xidian University, Xian, 710071, China)
Abstract: In order to achieve intelligent and efficient of seedling grafting process, a new mechanical structure scheme regarding the four-degree-of-freedom serial grafting robot is proposed. In view of the complexity of its structure, timing control and linkage operation, the module identification visualization method and design implementation with the architectural constraints is developed. Firstly, the design structure matrix (DSM) of the robot considering the specific architecture constraints is constructed, and a large community fast unfolding algorithm (LOUVAIN Algorithm) is used to realize the pre-division of the robot architecture blocks. Secondly, the DSM is clustered by using an advanced genetic algorithms (AGA), and multiple sets of high modularity divisions are obtained, which form a group possibility matrix (GLM). The diagonal GLM (DGLM) is obtained by diagonalizing GLM. Finally, the visualization strategy for DGLM is developed, and the colored optimal module division result is obtained. The optimal design result shows that the four-degree-of-freedom serial grafting robot should be divided into seven independent modules, and the modularity reaches 0.782.
Keywords: grafting robot; modular design; architectural constraints; genetic algorithms
0 引言
育苗嫁接设备及其技术开发是现代农业发展的重要方向,农业发达国家特别注重育苗嫁接工业技术发展,有不少不同结构的育苗嫁接机器人被提出并应用。如荷兰ISO Graft 1100型半自动嫁接机,采用转盘机构完成了砧木部分的连续作业流程,12个工位的转盘使得嫁接效率可达1 000株/h。但该嫁接机械设备具有独特的地域作物适用性要求,对秧苗的标准化要求很高,推广应用难度很大。近年来,国内部分研究人员也提出了一些育苗嫁接机器人的方法和技术。如姜凯等[1]设计了一种四手爪柔性夹持搬运机构,能够实现上苗、切削和对接工位同步作业,提高了机器嫁接效率,该机构嫁接平均速度为1 052株/h,是同类型单手爪嫁接机作业效率的1.72倍。李伯康等[2]基于Arduino单片机设计一种树苗硬枝嫁接机器人控制系统,可实现嫁接机器人砧木与穗木的夹持、搬运、定位、切苗、接合及捆绑作业。肖庆港等[3]提出采用机械手的形式实现对单株嫁接对象的抓取和嫁接定位,但其结构较为复杂,单株嫁接效率不高,对操作控制要求较大,缺少工程开发性。目前我国现代农业发展规划中,在降低劳动者强度和提升农业现代化水平目标指引下,果蔬育苗嫁接机器人的研发需求极为迫切;同时限于引进设备价格高昂且缺少适用性,具有自主知识产权的、高效的、自动化程度高的嫁接机器人现代设计方法成为农业科技发展亟待解决的基础科学问题[4]。基于此,本文拟提出一种四自由度串联果蔬育苗嫁接机器人,其作为一类复杂产品及系统,设计过程较为复杂,拟发展其模块化设计方法及给出其设计流程。
模块化设计是对产品进行更能分析,划分出一系列功能模块,来满足市场不同需求的设计方法[5]。复杂产品及系统的设计可以采用模块化设计方法,且已经得到了很好地应用。刘学敏等[6]基于现有花生收获机以及油莎豆收获机功能单一的特点,运用模块化设计方法,成功研制了一种振动筛式多功能收获机。张海燕等[7]以设计概念为主线,以功能—原理—行为—结构设计过程模型为映射获得系统零部件的综合相关关系矩阵,实现了变双曲圆弧齿线圆柱齿轮专用机床的快速模块化设计。Xu等[8]采用组遗传算法(GGA)将缠绕机部件聚类为标准化模块,以产品性能最好和成本最低为目标建立模块配置模型,实现了对缠绕机设计过程的快速重构。程贤福等[9]根据起重机抓斗结构及其零部件的复杂性,提出关联其设计过程的模块间解耦策略,提高了起重机抓斗的设计效率。Li等[10]提出了一种改进的Elbow方法来确定聚类过程中的最佳粒度水平和相应的模块度谱,基于现有文献实例和颚式破碎机模块化设计案例,进行了方法验证。由上述已有研究过程及结果可见,复杂产品及系统采用模块化设计方法能取得良好的设计结果,这为本文拟开展的嫁接机器人模块化设计方法及实现流程的提出提供了可供借鉴的理论基础,同时设计优化结果的实现也将为模块化设计过程中的算法优化及可视化方法发展提供实践参考。
模块化设计过程的核心在于模块识别算法的准确性和先进性[11],其直接决定了设计水平和效率。长期以来模块识别主要是基于模块设计结构矩阵DSM的聚类算法,如汪文旦[12]、Daie[13]、Wilschut[14]等分别提出了系统架构DSM聚类方法。近年来,一些新的优化模型被提出,如郏维强等[15]发展了基于模糊关联分析与求解的复杂产品模块化设计方法;王蕾等[16]提出了一种带供应商耦合约束遗传算法的再制造服务资源模块聚类优化模型;Zhang等[17]开发了一种基于DSM的模块化和排序算法;Li等[18]建立了复杂产品模块化的双目标优化模型。但已有的这些算法研究中,通常把产品构件之间的约束关系分为两类:第1类约束关系是两个元素必须配置在同一模块中,第2类是两个元素禁止配置到同一模块中;但这些基于聚类及优化算法的模块化设计方法并不能很好地处理复杂约束条件。因此,新的交互式模块划分方法被提出并逐渐发展起来,其过程一般为先用聚类算法自动生成模块划分方案,然后设计人员依据架构约束条件和产品知识对模块划分结果进行修正。如Sanaei等[19]采用新颖的交互式模块划分算法来处理架构约束条件;Sinha等[20]改进了两种聚类算法:社区监测算法(CDA)和IGTA,将多种设计约束纳入到改进的算法中,避免了不合理的模块划分结果。然而,分析其模块设计结果可发现这些划分算法与自动式的聚类算法一样无法直观地显示出多种潜在模块。
基于此,本文将在已经发展了模块边界约束条件下的DSM对角化排序优化算法[21]、架构约束条件下产品模块识别的可视化方法[22]及包含构件成组约束的多目标产品模块识别方法[23]等研究基础上,以嫁接机器人为具体的模块化设计对象,提出一种新的架构约束条件下的可视模块化设计方法。
1 四自由度串联嫁接机器人概念设计
1.1 嫁接机器人结构组成
兼顾嫁接机器人结构合理性和工作效率,概念设计过程通过分解功能指标获得求解方案集。育苗嫁接机器人功能需求:完成快速自动化上苗、定位、切割、对接、上夹、运输等时序动作;可嫁接成组秧苗(具体数量可调);节省劳动力和劳动强度,将人工嫁接所需的人工从2人下降到1人,工作时工人完成辅助简单工作流程,如手动上夹、在指定位置放置育苗盘等;嫁接效率不低于750株/h。
嫁接机器人概念设计过程中将其功能实现的结构分为四部分:定位、夹持、切削及运输结构。定义的四自由度分别为实现砧木和接穗苗的X-Y方向的运动、旋转切苗运动、升降平台Z方向运动等。这些运动过程按照时间先后顺序执行;因此此类机器人可归结为一类四自由度串联机器人结构及机电一体化复杂产品。
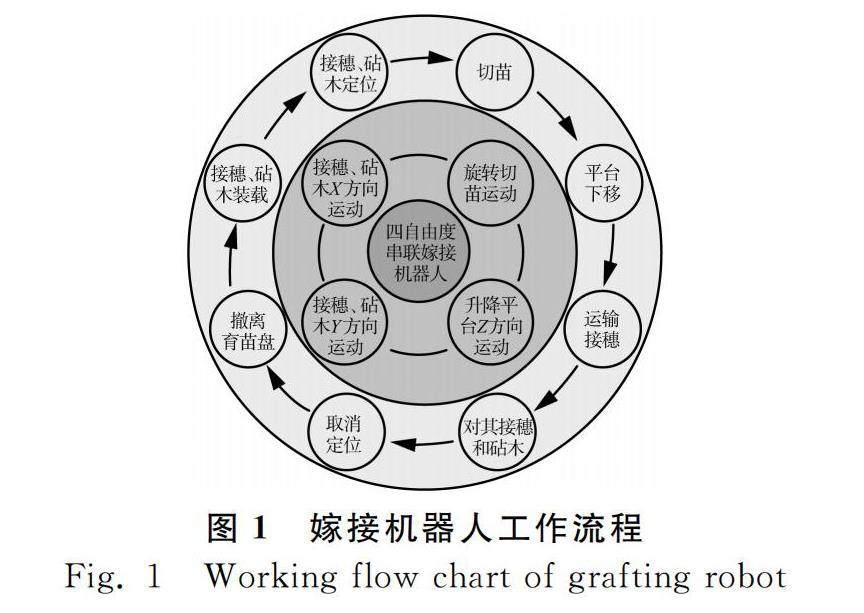
概念设计过程育苗嫁接机器人包括工作平台、夹持定位机构、旋转切苗机构、接穗运输机构等四个功能模块。按照功能—行为—结构的设计流程,对每个模块进行后续设计,细化的动作流程如图1所示,具体为定位、夹持、切削、运输与对接、固定嫁接苗等动作。
从图1可见,嫁接机器人的工作流程极为复杂,概念设计过程提出的四个功能模块的实现方案较多,如何设计最优模块结构将成为详细设计的核心,为此本文结合概念设计初步的构件及关联关系,对模块进行优化分析,得到最优的设计结果。
1.2 嫁接机器人设计结构矩阵
本文从四自由度串联嫁接机器人构件之间的结构关系和联动控制关系来构建设计结构矩阵。概念设计后的四自由度串联嫁接机器人一共包含74种构件,参与模块化设计的构件为68种。工作平台是总线型结构的构件,会对聚类结果产生影响,且该构件一般情况下没有设计变更需求,所以在初始化DSM的时候去除该元素,不参与模块化的设计;只与工作平台单独连接的支腿也不参与模块化的设计。螺栓、螺母、螺钉和轴承,这些通用件只起到了构件之间的连接作用,也不参与模块化的设计。
首先完成对构件之间的相关关系的量化,定义连接强度系数,强相关系数为1;弱相关系数为0.5;无相关系数则为0。即当构件之间具有连接关系、构件之间是直接驱动关系时,系数为1;如果构件之间是间接驱动关系,则设置为0.5。举例,旋转切苗机构中电机直接驱动主动齿轮且它们之间具有连接关系,故系数为1,但电机最终的目的是实现刀片的旋转,所以电机与刀片具有间接驱动关系,则系数为0.5。
2 架构约束下的模块识别可视化方法
2.1 架构约束条件
本文所提及的架构约束条件指的是构件之间的配置约束关系,具体定义为两类:第一类约束关系是构件对必须配置在同一个模块中,第二类约束关系是构件对禁止配置在同一个模块中。特别地,当一对构件之间具有比较强的相关关系,且一个构件发生设计变更时会导致另一个构件也需要发生设计变更时,它们之间的关系就属于第一类架构约束关系。第二类约束关系的一个重要体现是在安全协同设计的过程中,涉及机密参数的构件与共享参数的构件禁止配置到同一个模块中。
以四自由度串联嫁接机器人概念设计中的旋转切苗机构为例,对其约束条件的定义如下:旋转切苗机构的刀片和刀片支架之间具有强连接关系,且刀片发生尺寸和材料的设计变更时,刀片支架也会发生改变,故这两个构件之间具有第一类约束关系。控制切苗机构发生上下移动的传功杆,其运动方式是沿Z轴的平移;切削砧木和接穗苗的刀片,其运动方式是沿X轴的旋转;且他们之间不存在直接或间接的耦合关系,所以这两个构件之间具有第二类约束关系,禁止划分到同一模块中。
2.2 预模块划分
在传统的模块化设计中,模块数是通过人为的方式预先定义的,但当产品系统具有较复杂的结构时,无法准确地定义模块数。鉴于处理图2所示完整DSM矩阵模块化的复杂性和收敛性,本节先采用LOUVAIN算法[24]进行预模块划分,该算法的优点在于单次运行的时间较短,其结果可以为后续完整的自动聚类算法提供所需的最大模块数和优质解阈值。
2.2.1 聚类准则
采用模块度增量ΔQ函数作为聚类准则,即[24]
ΔQ=∑C,in+2ki,in2m-∑C,tot+ki,tot2m2-∑C,in2m-∑C,tot2m2-ki,tot2m2(1)
式中:∑C,in——被划分到模块C内的所有构件之间的连接强度系数之和;
∑C,tot——模块C内所有构件与模块C外所有构件之间的连接强度系数之和;
ki,tot——构件i与其他所有构件之间的连接强度系数之和;
ki,in——构件i和模块C内所有构件的连接强度系数之和;
m——所有构件的连接强度系数之和。
采用模块度Q函数作为聚类准则,即[24]
Q=12m∑i,j∈VAij-kikj2mδci,cj(2)
m=∑i,j∈VAijki=∑j∈vAij
式中:V—— DSM中所有构件的集合;
Aij—— DSM中的构件i、j之间的连接强度系数;
ci——构件i所划分到的模块序号。
如果ci=cj,即表明构件i、j划分在同一模块中,定义δci,cj=1,其他情况δci,cj=0,Q的最大值为1,Q值越大则模块化程度越高。
2.2.2 算法实现过程
步骤1:初始化形成构件初始模块。将每个构件i分配为不同的子模块,形成初始模块。
步骤2:初始模块合并与移除处理。对每个构件i,计算分析将i从其模块中移除并加入与i有相关关系的构件j所在的模块中所带来的模块化增益ΔQ。
步骤3:确定模块合并位置。将i放到ΔQ最大(ΔQmax)的模块中,如果产生的ΔQmax<0则将它放在原来的模块。对所有节点重复并顺序地应用此过程,直到没有构件发生移动。
步骤4:建立模块网络。模块中的每个节点对应于步骤3中确定的模块合并位置,节点之间的相关关系为步骤3中两个模块中的构件之间的相关关系之和,节点内部的相关关系为步骤3模块内所有构件的相关关系之和。
步骤5:计算模块网络的模块度Q。重复步骤1到步骤4,直到模块网络的模块度Q不再增加为止。
2.2.3 举例
旋转切苗结构由17种构件组成,用字母a~q分别代表这些构件。图2为旋转切苗结构的原始DSM。
LOUVAIN算法基于Python语言开发,运行算法的计算机平台系统配置为Intel? CoreTMi5-7200U CPU(2.5 GHz),4 GB RAM(后续算法的实现平台均为此),耗时约0.015 s,优化后的模块度Q=0.462,图3给出了具体的模块划分可视化结果,划分到同一模块的构件用相同颜色标记。
由图3可见,第一次聚类将旋转切苗结构划分为6个模块,模块度为0.413;第二次聚类将旋转切苗结构划分为3个模块,模块度为0.462;第三次聚类将旋转切苗结构划分为1个模块,模块度为0;算法结束。将旋转切苗机构划分为{a, b, c, d, e}、{f, g, h, i, k}、{j, l, m, n, o, p, q}的模块划分方案具有比较明显的模块化结构。基于此结果,本文采用自动聚类算法时将最大模块数Nmax设置为3,优质解阈值设置为0.462。
2.3 自动聚类实现
本文提出并采用遗传算法进行自动聚类,采用模块度Q函数作为聚类准则,其具体的实现过程及举例如下。
2.3.1 DSM预处理
1) 对原始DSM矩阵进行预排序,使得满足第一类约束条件的构件沿着对角线分布在一起,形成最小聚类单元。举例,如图2所示的原始DSM,其架构约束条件为构件b(刀片支架)和构件c(刀片)必须放到一个模块中,构件c(刀片)和构件j(传动杆)禁止放到一个模块中。为此,预处理后的DSM如图4所示,则其最小聚类单元为[b,c]、[j]、[a]、[d]、[e]、[f]、[g]、[h]、[i]、[k]、[l]、[m]、[n]、[o]、[p]、[q]。
2) 定义最小聚类单元的边界点索引矢量。图4的索引矢量定义为index=[0, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]。如此本例中原17个构件的聚类问题将转换为16个构件的聚类问题,这不仅能很好地体现第一类架构约束条件,也能缩小算法的搜索范围;当约束条件较多时,效果更突出。
2.3.2 遗传算法的实现过程
1) 初始化。种群包含Np个个体,将种群初始化,每一个个体中的最小聚类单元被随机分配一个模块标号。
2) 染色体编码。个体染色体编码如图5所示。每一位上的数值代表该基因位上对应的构件模块标号。模块标号是整数,其取值范围为0~Nmax-1,这里的Nmax是由上文LOUVAIN算法确定的最大模块数。在最小聚类单元中的构件必须具有相同的模块标号。
3) 交叉和变异算子。本文采用多点交叉算子,并将约束条件考虑在内。由于数据量的变化,为了增大算法搜索范围,交叉点的个数会有调整。交叉点的位置在染色体每一个基因边界,这里由于考虑到第一类约束条件,故交叉点的位置为最小聚类单元的边界。算法随机选择交叉点,对父代染色体进行交叉操作。本文将违反第二类约束条件的个体的模块度设置为0,因此其适应度的值也为0。
变异算子也采用多点方式,首先随机选取一个基本位,将0~Nmax-1之间产生的一个随机数替换此基因位上的模块标号;然后重复多次。变异点的个数也随着数据量的变化而变化。如果违反第二类约束条件,将该变异后的个体模块度设置为0。
2.3.3 算法举例
使用遗传算法对预排序后的DSM(图4)进行自动聚类,该算法运行约17 s,将Q>0.462的模块划分方案作为优质解,满足架构约束条件的优质解如图6所示。从图6可以看出,构件g的划分比较灵活。对于旋转切苗结构产生的优质解较少,设计者可以通过人工筛选来确定最终的模块划分方案。但是对整个嫁接机器人系统展开模块化设计会产生比较多的优质解,通过人工筛选的方式来确定最终的模块划分方案难以实现。下文将对产生的优质解集进行处理,基于优质解集建立GLM,将GLM进行对角化排序,最后对DGLM进行模块识别,以确定最终的模块划分方案。
2.4 对角化排序
利用优质解集来捕获2个构件分配到同一模块的可能性,这种可能性反映了一对构件之间的耦合强度[19]。GLM中的非对角单元记录了一对构件之间的耦合强度。将GLM进行对角化排序,并对DGLM着色可以看出清晰的可视化模块结构。本文中对角化排序算法采用改进的遗传算法,此遗传算法与上文采用的遗传算法的区别在于交叉算子和变异算子的优化选择处理。
2.4.1 计算GLM
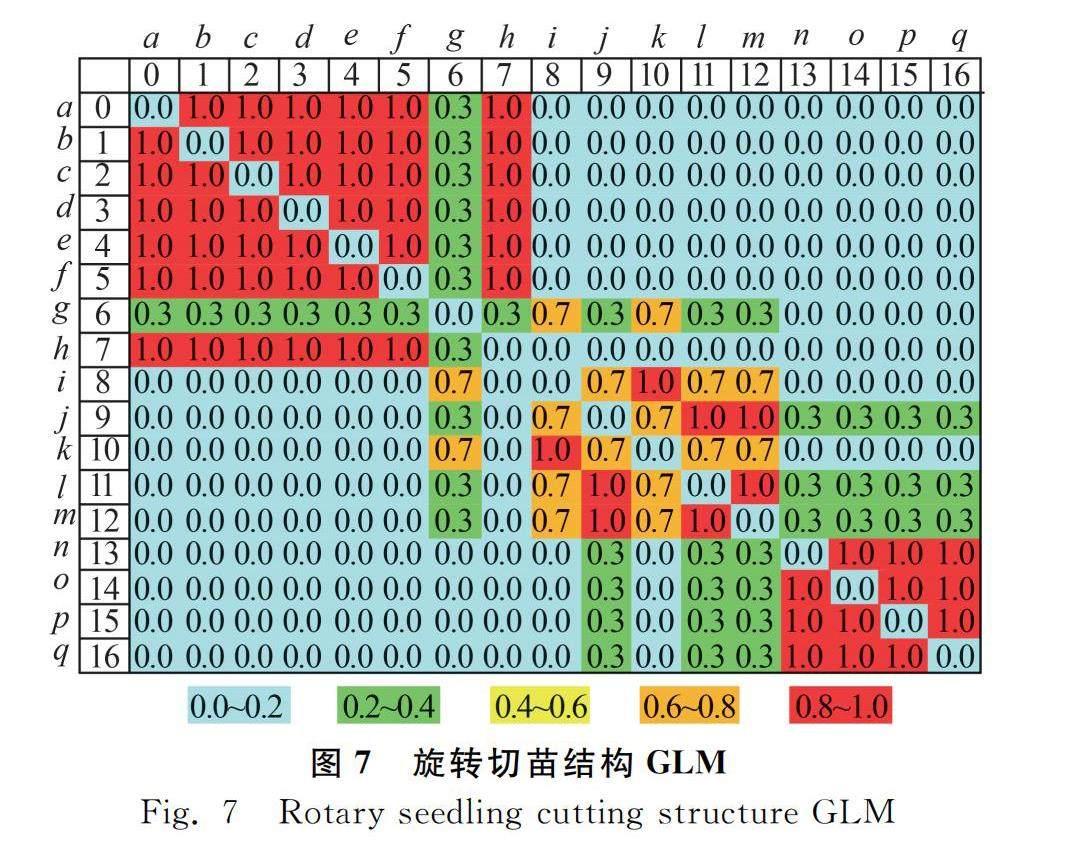
GLM记录了优质解集中不同构件划分在一个模块中的可能性,GLM中元素的取值范围为[0,1],如图7所示。一共有n个优质解,其中有m个优质解将构件i和构件j划分在了一个模块中,其成组可能性则为m/n。
2.4.2 对角化准则
根据下面的对角化准则进行对角化排序
C=∑Ni=1∑Nj=1(|j-i|×ωij)(3)
式中:N——GLM中元素的个数;
i、j——GLM中的行指针和列指针;
ωij——GLM中的元素。
2.4.3 遗传算法
采用改进的遗传算法来求解GLM的对角化排序问题。
1) 染色体编码。染色体编码如图8所示。每一条染色体代表的是构件标号产生的随机序列。
2) 种群初始化。按照染色体编码格式随机产生 Np个个体,因为自动聚类算法产生的优质解集已经满足了架构约束条件,所以对角化排序无需考虑架构约束条件。
3) 交叉和变异算子。本文采用两点交叉算子,如图9所示。交叉点的位置为每个基因位的边界。采用两种交叉方式进行交叉[25]:(1)选择两个随机位置,被选中的两点之外的染色体段为父代1所固有的,其余的基因序列按照父代2中的基因序列放置到两点之内的染色体段中;(2)选择两个随机位置,被选中的两点之内的染色体段为父代1所固有的,其余的基因序列按照父代2中的基因序列放置到两点之外的染色体段中。
采用两种交叉方式的概率都为0.5。
变异算子采用移位变异算子[26],如图10所示,随机选择两个位置,将染色体中某一位置上的基因删除然后插入到另一位置上。
2.5 可视化模块识别
通过遗传算法对GLM进行排序得到最优排序,算法耗时约8 s,优化后的对角化准则C=213.5,得到可视化的DGLM如图11所示。设定一个成组可能性阈值,将大于某一阈值的构件对配置在同一模块。
以0.6为阈值[22],可以看出清晰的模块边界有{a, h, f, d, e, c, b},{p, q, o, n}。构件k、i同时与构件g和块{j, m, l}具有高的成组可能性。因为交叠项较大,所以将它们配置在同一模块中。最终将旋转切苗机构划分为三个模块,模块度为0.482,得到的模块划分方案为{a, h, f, d, e, c, b},{g, k, i, j, m, l},{p, q, o, n}。
2.6 总体流程
总体流程如图12所示。
本文提出并采用不同算法实现的模块化设计的具体流程,其中的主要步骤为:首先,利用LOUVAIN算法进行预模块划分;其次,采用遗传算法自动聚类得到一组满足架构约束条件且高模块度的模块划分方案(优质解集);再次,计算GLM并将其对角化,对角化排序算法采用改进的遗传算法;最后,对DGLM进行着色处理,获得最合理的模块划分方案。
3 嫁接机器人的模块化设计过程
针对本文提出的四自由度串联嫁接机器人概念设计结构,进行整机原始DSM(图1)的模块化优化设计,具体设计过程如下。
3.1 预模块划分
使用LOUVAIN算法进行预模块划分。算法运行约0.5 s,第一次聚类将四自由度串联嫁接机器人划分为18个模块,模块度为0.630;第二次聚类将嫁接机器人划分为7个模块,模块度为0.782;第三次聚类将嫁接机器人划分为4个模块,模块度为0.723;算法结束。将嫁接机器人划分为7个模块的划分方案具有比较明显的模块化结构。因此后续模块划分中将最大模块数Nmax设置为7,将优质解阈值设置为0.723。
3.2 自动聚类实现
使用遗传算法进行自动模块划分。算法运行约20 min,产生63个模块划分方案(优质解)。最大优质解的模块度为0.773,最小优质解的模块度为0.725。
3.3 对角化排序
用优质解集建立GLM,然后使用改进的遗传算法进行对角化排序,建立DGLM,并对DGLM进行着色处理,如图13所示。算法运行约4 min,对角化准则C=4 158。
3.4 可视化模块识别
对DGLM进行模块识别,以0.6作为构件配置在同一模块的可能性阈值[22]。可以看出四自由度串联嫁接机器人边界清晰的模块有{0, 1, 2, 3, 4, 5, 7},{8, 9, 10, 11, 12, 13, 14, 15, 16},{17, 18, 19, 21, 22, 23},{39, 40, 41, 42, 43, 44, 45, 46},{47, 48, 49, 50, 51},{52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67}。
构件6与块{8, 9, 10, 11, 12, 13, 14, 15, 16}和{0, 1, 2, 3, 4, 5, 7}同时具有比较高的成组可能性。为了避免过大的模块,将这两个块独立。可以将构件6与块{8, 9, 10, 11, 12, 13, 14, 15, 16}划分在一个模块中或者与块{0, 1, 2, 3, 4, 5, 7}划分在一个模块中。从结构稳定性的角度出发将构件6与块{0, 1, 2, 3, 4, 5, 7}配置到一个模块中。
构件33、构件21和块{20, 25, 26, 27, 28, 29, 30, 31, 32, 34, 35, 36, 37, 38}同时具有比较高的成组可能性,但是构件33和块{17, 18, 19, 21, 23}之间的成组可能性不高,且为了避免过大的模块,所以将构件33与块{20, 25, 26, 27, 28, 29, 30, 31, 32, 34, 35, 36, 37, 38}配置到一个模块中。
构件24只与构件20具有耦合关系,所以构件24应该划分到构件20所在的模块中。
最终将四自由度串联嫁接机器人划分为7个模块:{0, 1, 2, 3, 4, 5, 6, 7},{8, 9, 10, 11, 12, 13, 14, 15, 16},{17, 18, 19, 21, 22, 23},{20, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38},{39, 40, 41, 42, 43, 44, 45, 46},{47, 48, 49, 50, 51},{52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67};该模块划分方案的模块度为0.782。具体的嫁接机器人模块划分方案如表1所示。
图14给出了基于优化模块化设计结果四自由度串联嫁接机器人整体结构方案,用不同的颜色对不同的模块加以区分。
整机运动驱动部分由8个电机和4个舵机驱动构成,实现了四个自由度的控制。8个电机实现了X轴定位与运输机构的沿X方向的夹持运动和沿Y方向的往复运动、Y轴定位与运输机构的沿Y方向的夹持运动和沿X方向的往复运动、升降式平台和旋转切苗结构的上下往复移动。4个舵机实现了旋转切苗机构旋转切削运动。
结合此总体结构,提出的嫁接机器人控制动作流程如下:(1)传送带将两个育苗盘送入升降台指定位置处,然后按下开关按钮,机器开始工作,耗时3 s;(2)两侧Y轴运输机构向中间移动,同时夹板插入幼苗间隙,耗时2 s;(3)Y轴定位机构与X轴定位机构的上下两层夹板交错运动,靠拢夹紧幼苗根茎,耗时1 s;(4)旋转切苗运输机构向下移动到工作位置,刀具旋转开始切断接穗和砧木,然后旋转切苗机构上移回到原来位置,耗时6 s;(5)X轴运输机构向左移动,升降台下移,把切好的接穗苗运输到砧木根茎所在位置,X轴运输机构向右移动升降台上移,耗时5 s;(6)工人使用塑料夹一一固定幼苗,完成确认后各机构复位,工人撤离育苗盘,准备下一轮嫁接,耗时28 s;(7) 轮嫁接共耗时45 s,共嫁接10株秧苗(育苗盘2×5穴),效率为800株/h。
采用问卷调查的方式,对本文嫁接机器人模块化设计结果进行评价。调查对象包括机械设计专家、从事嫁接技术专家和嫁接操作人员等(26人)。调查结果如表2所示。
对问卷调查结果的分析可见,嫁接机器人的模块划分结果是较为合理的,但模块数是否为做优解还有一定的不确定性,这与模块划分过程中阈值的选择有关,本文参照前期研究选用0.6,但实际需要结合后期机器人的运行、维护等表现做具体细化。模块化设计过程中定义的架构约束关系可能不能恰当处理诸如索、绳等柔性单元,故通用性有待提高。但设计结果展示了好的可视化效果,也有利于机器人复杂系统后续更新,具有好的实践性。
4 结论
1) 提出一种架构约束下的模块识别可视化方法。其特点是采用LOUVAIN算法进行预模块划分,基本的遗传算法实现嫁接机器人的自动聚类,改进的遗传算法实现GLM的对角化排序。该设计方法能较好地解决设计人员在模块化设计过程中需要调整模块数的弊端;通过可视化的DGLM更好地表达育苗嫁接机器人的内部耦合关联和整体协同关系。
2) 发展了适用于排序的改进遗传算法,该算法将优化选择两点交叉和移位变异算子,结果表明其显著提高了设计效率,完成嫁接机器人整体GLM排序用时约4 min。同时,基于此结果给出的模块识别可视化原则具有较好的可行性,实现了对于结果的直观展示。
3) 模块化设计结果显示四自由度串联嫁接机器人应划分为7个模块:旋转切苗机构运输模块、旋转切苗模块、Y轴运输模块、Y轴定位模块、育苗盘升降模块、X轴运输模块、X轴定位模块等,模块度达到了0.782。研究结果对于嫁接机器人的多方协同设计与研发、产品族的改进和系列化发展具有重要的工程指导价值。
参 考 文 献
[1]姜凯, 陈立平, 张骞, 等. 蔬菜嫁接机器人柔性夹持搬运机构设计与试验[J]. 农业机械学报, 2020, 51(S2): 63-71.
Jiang Kai, Chen Liping, Zhang Qian, et al. Design and experiment on flexible clamping and conveying mechanism of vegetable grafting robot [J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51 (S2): 63-71.
[2]李伯康, 赵颖, 孙群. 树苗硬枝嫁接机器人控制系统设计[J]. 中国农机化学报, 2016, 37(2): 186-190.
Li Bokang, Zhao Ying, Sun Qun. Design a control system for a sapling branch grafting robot [J]. Journal of Chinese Agricultural Mechanization, 2016, 37(2): 186-190.
[3]肖庆港, 周建平, 李明, 等. 一种高效嫁接机器人[P]. 中国专利: CN209964697U, 2020-01-21.
[4]张国渊, 邹永成, 梁茂檀, 等. 一种半自动化嫁接机器人[P]. 中国专利: CN112449895B, 2022-04-01.
[5]程贤福, 罗珺怡. 考虑两两模块之间关联关系的产品模块划分方法[J]. 机械设计, 2019, 36(4): 72-76.
Cheng Xianfu, Luo Junyi. Method of product module partition based on the relationship between two modules [J]. Journal of Machine Design, 2019, 36(4): 72-76.
[6]刘学敏, 刘志辉, 梁燕, 等. 基于模块化设计理念的多功能收获机开发[J]. 中国农机化学报, 2012, 43(5): 47-50.
Liu Xuemin, Liu Zhihui, Liang Yan, et al. Development of multifunctional harvesting machine based on modular theory [J]. Journal of Chinese Agricultural Mechanization, 2012, 43(5): 47-50.
[7]张海燕, 侯力, 罗岚, 等. 变双曲圆弧齿线圆柱齿轮专用机床的模块化设计[J]. 机械工程学报, 2021, 57(3): 77-86.
Zhang Haiyan, Hou Li, Luo Lan, et al. Modular design for machine tools of variable hyperbolic circular-arc-tooth-trace cylindrical gear [J]. Journal of Mechanical Engineering, 2021, 57(3): 77-86.
[8]Xu Xiaoming, Zhang Wuxiang, Ding Xilun. Modular design method for filament winding process equipment based on GGA and NSGA-Ⅱ [J]. International Journal of Advanced Manufacturing Technology, 2018, 94(5-8): 2057-2076.
[9]程贤福, 万冲, 邱浩洋, 等. 模块化产品设计中模块间的关联分析与解耦策略[J]. 计算机集成制造系统, 2020, 26(4): 1043-1051.
Cheng Xianfu, Wan Chong, Qiu Haoyang, et al. Association analysis between modules and decoupling strategies in modular product design [J]. Computer Integrated Manufacturing Systems, 2020, 26(4): 1043-1051.
[10]Li Zhongkai, Wei Wenyuan. Modular design for optimum granularity with auto-generated DSM and improved elbow assessment method [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2022, 236(4): 413-426.
[11]顾新建, 马步青, 顾复, 等.产品模块化中的若干智能方法[J]. 机械工程学报, 2021, 57(17): 1-9.
Gu Xinjian, Ma Buqing, Gu Fu, et al. Some intelligent methods in product modularization [J]. Journal of Mechanical Engineering, 2021, 57(17): 1-9.
[12]汪文旦, 秦现生, 阎秀天, 等. 一种可视化设计结构矩阵的产品设计模块化识别方法[J]. 计算机集成制造系统, 2007, 13(12): 2345-2350.
Wang Wendan, Qin Xiansheng, Yan Xiutian, et al. Visual design structure matrix method for product design modules identification [J]. Computer Integrated Manufacturing System, 2007, 13(12): 2345-2350.
[13]Daie P, Li S. Matrix-based hierarchical clustering for developing product architecture [J]. Concurrent Engineering Research and Applications, 2016, 24(2): 139-152.
[14]Wilschut T, Etman L, Rooda J E., et al. Multi-level flow-based markov clustering for design structure matrices [J]. Journal of Mechanical Design, 2017, 139(12): 121402.
[15]郏维强, 刘振宇, 刘达新, 等. 基于模糊关联的复杂产品模块化设计方法及其应用[J]. 机械工程学报, 2015, 51(5): 130-142.
Jia Weiqiang, Liu Zhenyu, Liu Daxin, et al. Modular design method and application for complex product based on fuzzy correlation analysis [J]. Journal of Mechanical Engineering, 2015, 51(5): 130-142.
[16]王蕾, 夏绪辉, 熊颖清, 等. 再制造服务资源模块化方法及应用[J]. 计算机集成制造系统, 2016, 22(9): 2204-2216.
Wang Lei, Xia Xuhui, Xiong Yingqing, et al. Modular method of remanufacturing service resources [J]. Computer Integrated Manufacturing System, 2016, 22(9): 2204-2216.
[17]Zhang Xiaojin, Ma Shuang, Chen Songlin. Healthcare process modularization using design structure matrix [J]. Advanced Engineering Informatics, 2019, 39: 320-330.
[18]Li Yupeng, Ni Yongbo, Zhang Na, et al. Modularization for the complex product considering the design change requirements [J]. Research in Engineering Design, 2021, 32(4): 507-522.
[19]Sanaei R, Otto K N., H?ltt?-Otto K, et al. Incorporating constraints in system modularization by interactive clustering of design structure matrices [C]. Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2016.
[20]Sinha K, Han S Y, Suh E S. Design structure matrix-based modularization approach for complex systems with multiple design constraints [J]. Systems Engineering, 2019, 23(2): 211-220.
[21]卫军朝, 张国渊, 闫秀天. 模块边界约束条件下产品设计结构矩阵排序算法[J]. 制造业自动化, 2017, 39(12): 106-110.
Wei Junchao, Zhang Guoyuan, Yan Xiutian. Product design structure matrix sorting algorithm under boundary constraints of modules [J]. Manufacturing Automation, 2017, 39 (12): 106-110.
[22]卫军朝, 张国渊, 闫秀天. 架构约束条件下产品模块识别的可视化方法[J]. 计算机辅助设计与图形学学报, 2018, 30(5): 936-945.
Wei Junchao, Zhang Guoyuan, Yan Xiutian. A visual method for identifying modules considering architectural constraints [J]. Journal of Computer-Aided Design and Computer Graphics, 2018, 30(5): 936-945.
[23]卫军朝, 闫秀天, 张国渊. 包含构件成组约束的多目标产品架构模块划分[J]. 计算机集成制造系统, 2018, 24(12): 3096-3106.
Wei Junchao, Yan Xiutian, Zhang Guoyuan. Multi-objective module division method for product architecture incorporating component grouping constraints [J]. Computer Integrated Manufacturing Systems, 2018, 24(12): 3096-3106.
[24]Blondel V D, Guillaume J L, Lambiotte R, et al. Fast unfolding of communities in large networks [J]. Journal of Statistical Mechanics: Theory and Experiment, 2008(10): 10008.
[25]Murata T, Ishibuchi H. Performance evaluation of genetic algorithms for flowshop scheduling problems [C]. IEEE World Congress on Computational Intelligence, 2002.
[26]Larranaga P, Kuijpers C M H, Murge R H, et al. Genetic algorithms for the travelling salesman problem: A review of representations and operators [J]. Artificial Intelligence Review, 1999, 13(2): 129-170.
DOI: 10.13733/j.jcam.issn.2095-5553.2024.06.030
崔海朋, 秦朝旭, 马志宇. 基于深度学习的鱼类特征点检测与体征识别方法[J]. 中国农机化学报, 2024, 45(6): 201-207
Cui Haipeng, Qin Chaoxu, Ma Zhiyu. Fish key feature point detection and sign identification based on deep learning [J]. Journal of Chinese Agricultural Mechanization, 2024, 45(6): 201-207
