基于具身认知理论的高中数学生本课堂*

【摘 要】圆锥曲线与方程是高中数学的重要内容之一。研究圆锥曲线有两个重要任务：一是研究它的概念及其标准方程，二是研究其性质。在研究的过程中，教师可以基于具身认知理念，引导学生通过体悟、探索、实验以及迁移，实现自主探究学习、深度学习，从而落实数学核心素养的培养，打造生本课堂。

【关键词】高中数学；概念数学；椭圆；具身认知；核心素养

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2024）15-0041-04

【作者简介】崔绪春，江苏省清江中学（江苏淮安，223001）教师，正高级教师。

“具身认知”（Embodied Cognition）指人类思维和感知过程不仅来自于大脑神经系统，还与身体的运动、肌肉和感知器官的活动密切相关。具身认知理论启示教师要不断创造条件，鼓励学生通过多种感官训练手段去体悟、探索、实践，从而促成探究学习、深度学习。［1］下面笔者以苏教版高中数学选择性必修一“椭圆概念”教学为例，阐述“具身认知”理论下的高中数学生本课堂的实践探索。

一、教学分析

（一）教学内容分析

圆锥曲线是高中数学的重要内容之一，研究圆锥曲线不是用规律推理形式，而是运用代数方法解决几何问题，即用方程的解来表征几何结论，这是“数形结合”思想的重要体现。“椭圆概念”是圆锥曲线章节起始课，由于椭圆与双曲线、抛物线是同构的，研究好椭圆的概念及其标准方程，对本章后续知识的学习具有基础性与示范性作用。教材中直接给出椭圆定义，学生容易“知其然”但“不知其所以然”，对椭圆几何属性的认知不够透彻。因此，教学中笔者参考教材的章节导入内容，尝试依据历史上数学家对于椭圆几何性质的探究，带领学生从具体情境中抽象出椭圆的几何本质，经历完整的椭圆概念生成过程。

（二）教学目标

1.初步了解椭圆等圆锥曲线的现实背景，感知椭圆等圆锥曲线在解决具体问题和表述现实世界方面的作用；

2.以具身认知理论为指导，通过“旦德林双球”实验，引导学生抽象、归纳出椭圆的定义，并能够用恰当的自然语言、符号语言进行表征。

二、教学流程

（一）课堂引入：看一看

播放视频：“天问一号”成功进入预定轨道。

师：“天问一号”在苍穹中划过了一道优美的曲线（如图1），这条轨道曲线叫什么名字？

【设计意图】通过观看视频，学生了解了我国的火星探测工程，了解了圆锥曲线的航天应用，在引入新课的同时，激发了学生的爱国情怀和民族自豪感。

（二）问题提出：说一说

师：卫星运行的轨迹是椭圆。生活中还有哪些椭圆？请举例说明。

生：油罐车横截面，阳光斜照下篮球的影子，斜削火腿肠截面，鸡蛋的纵截面……

师：同学们善于用数学眼光观察世界，举的例子都很好！但是你能确定这些例子都是椭圆吗？是不是只要把圆压扁一点就是椭圆呢？究竟什么样的图形才是椭圆？让我们带着这些问题开始今天的学习。

【设计意图】上述教学旨在引导学生提出问题。通过对话，引发学生的认知冲突，让学生自然而然产生这些问题，引导他们从数量关系上定量地去思考椭圆，实现学生自主探究学习。

（三）实验感知：想一想

师：同学们，“跟着感觉走”明显不行，我们必须从数量关系上定量地去思考椭圆的定义。如何从数量关系上定义椭圆？椭圆有什么性质？为了解决这个问题，历史上很多数学家深入探究，通过数量关系描述了椭圆上的点的规律。这个规律是什么呢？现在就让我们一起沿着数学家走过的历程，揭开它神秘的面纱。

1.知识预备

如图2，在一个圆锥内，上下放置两个小球，容易得到：它们与圆锥侧面的公共点形成两个圆，我们把这两个圆记作圆C1和圆C2。［2］

学生分小组讨论研究以下问题。

【问题1】圆C1与圆C2所在平面平行吗？

【问题2】取圆C1与圆C2之间的线段PQ，让PQ与圆锥母线平行，请问PQ与两小球相切吗？

【问题3】若将线段PQ保持与圆锥母线平行，绕着圆锥的侧面转动一圈，线段PQ的长度变不变？为什么？

2.椭圆几何性质的探索

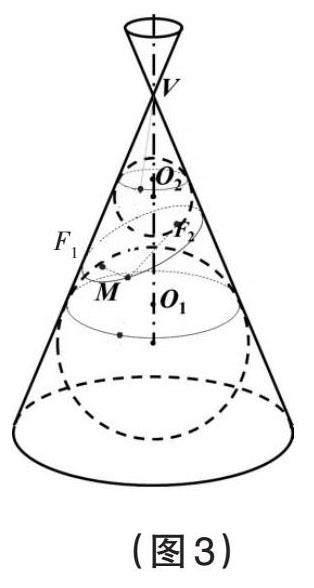
操作1：如下页图3，在图2基础上，用一个平面斜截圆锥得到椭圆形交线，并让椭圆所在平面与两个小球相切，记切点为F1，F2，在椭圆上任取一点M，连接MF1，MF2。

操作2：如下页图4，现在过点M作之前那样的PQ，由之前得到的结论：MF1，MP都与上方小球相切，所以│MF1│=│MP│（切线长相等），同理，│MF2│=│MQ│。

师：通过观察推理可得，当点M在椭圆上运动时，MF1，MF2分别与上下两个小球总相切。现在，让我们想一想刚才的问题“能否用数量关系表示椭圆上的点的运动规律？”请同学们按照小组，继续讨论以下问题。

【问题4】除了线段PQ的长度之外，在椭圆所在平面内，还有什么几何量是不变的吗？

【问题5】当点M在椭圆上运动时，点F1，F2的位置不发生变化。能否用语言描述一下：椭圆上的点应具有怎样的性质呢？

学生通过对问题的自主探究和交流讨论得到椭圆的性质：椭圆上的任意一点到两个定点的距离之和为常数，其中两个定点叫作椭圆的焦点，焦点之间的距离称为焦距，即：│MF1│+│MF2│=│MP│+│MQ│=│PQ│= 定值。

3.了解数学史

师：同学们，这个数学实验是19世纪比利时数学家旦德林给出的，旦德林在圆的切线与圆锥等领域研究上取得了突出成就，闻名世界的“旦德林双球”就是用他的名字命名的，我们要学习数学家旦德林勇于探索的创新精神。正是因为通过一平面截圆锥面，可以得到椭圆、双曲线、抛物线，所以椭圆、双曲线、抛物线才被称为圆锥曲线。

【设计意图】通过圆锥背景下的“旦德林球”，探索并发现椭圆的本质特征是本节课的难点。学生了解椭圆发展史上旦德林的经典证明，体会数学家巧妙的数学方法——构造法，并进行数学文化渗透。

（四）数学建构：画一画

师：同学们，通过刚才的实验，我们研究出了椭圆的几何性质，即椭圆上的任意一点满足到两定点距离之和为定值的数量关系。反过来，满足这一数量关系的点的轨迹是否是椭圆呢？下面我们来画椭圆，看看满足条件的点的轨迹是否为椭圆。

活动方案：（1）拿出准备好的硬纸板、图钉、细线；（2）用图钉固定好F1、F2，把细线两端固定在图钉上，用笔撑直绳子，同桌两人共同配合，让笔与绳之间是自由运动的，这样转动一周，画出的图形就是椭圆（如图5）。

学生在活动探究的基础上思考以下问题。

【问题6】画椭圆时，PF1，PF2的距离之和为什么要大于点F1，F2之间的距离？

【问题7】为什么这样画出来的图形就是椭圆？

师：平面内到两个定点F1，F2的距离之和等于常数2a（2a大于│F1F2│）的点的轨迹叫作椭圆。两个定点F1，F2叫作椭圆的焦点，两个焦点间的距离叫作椭圆的焦距。当2a =│F1F2│时，轨迹为线段F1F2；当2a＜│F1F2│时，轨迹不存在。

【设计意图】通过画椭圆的活动，学生对椭圆的本质特征有了更深刻的认知，更直观地体会了椭圆定义，为后续研究椭圆标准方程作铺垫。

（五）知识应用：做一做

例1：若动点M（x，y）到定点F1（-4，0）和F2（4，0）的距离的和为10，则动点M的轨迹为（    ）

A.椭圆   B.双曲线   C.线段   D.圆

变式1：动点M（x，y）到定点F1（-4，0）和F2（4，0）的距离的和为8，则动点M的轨迹是      。

变式2：动点M（x，y）到定点F1（-4，0）和F2（4，0）的距离的和为6，则动点M的轨迹是      。

变式3：方程[x2+（y+4）2]+[x2+（y-4）2]=10表示的曲线是      。

【设计意图】通过几道题目，学生进一步明确椭圆的定义，在概念的辨析中增强学生对椭圆概念的理解与记忆，为后续推导椭圆的标准方程作铺垫。

（六）反思提炼：悟一悟

（1）同学们，请回顾今天的学习内容，大家有哪些收获？

（2）诗歌欣赏：

椭圆

偏行已是欲离辙，浩瀚星空藉此歌。

一种相思天注定，月盈之夜两心合。

三、教学反思

（一）基于具身认知，促进学生深度学习

上述教学基于“具身认知”理论，通过椭圆性质探究、画椭圆等数学实验，让学生沿着数学家的思路探究、归纳椭圆的概念。教学以展示学生的研究成果为主，教师主要引导学生在探究的过程中逐渐形成观察发现、积极思考的习惯。这个过程既发展了学生数学概括、抽象能力和合作意识，又落实了教学核心素养培养要求。当视觉、听觉、直觉、身体都共同作用时，学生脑中烙下了深刻的印象，这样的教学很大程度上提高了学习的深度，让学习活动真正发生。

（二）突出主体地位，促使学生主动发展

本节课突出学生主体，所有问题都是学生自己动手、动脑去探索和“再创造”的。在这样的教学情境下，学生的思想是开放的、灵活的，能产生更多的“生成的东西”，能体验到更多成功感和愉悦感。这种教学法与传统的以教师为中心的教学相比，有以下优点：以学生为中心，有效调动了学生学习的积极性；有利于发展学生的数学思维能力；培养了学生的合作学习意识；培养了学生的主动探究意识与创新精神。［3］

（三）设计链式问题，促使学生思维创新

根据“学生最近发展区”理论，笔者为了让学生理解旦德林双球实验，突破难点，精心设置了7个问题，形成了问题链，步步相连、逐步推进，这不仅有利于启迪学生的思维，还能加深学生对椭圆本质的认识，同时通过这些问题的解决，巩固了学生对椭圆概念的理解，有效地激发学生自己去探索、研究。笔者认为在课堂教学中，教师提出的问题，就要像一根链条，每个问题都是链条上的一环，环环相扣，步步相依，由浅入深，拾级而上，呈现梯度性。这样能够充分暴露学生的思维过程，拓展学生的数学思路。

【参考文献】

［1］李昱蓉.具身学习：立足学科核心素养的学习方式［J］.当代教育科学，2017（9）：7-10.

［2］徐迪斐.“圆锥曲线”起始课教学设计［J］.中国数学教育，2015（10）：2-8.

［3］崔绪春.新课程理念下课堂上如何启迪学生的数学思维［J］.中学数学，2014（17）：12-13.