深水钻井隔水管横向振动振型分析
2024-06-07韩春杰姜继帅袁建马文倩荆国林
韩春杰 姜继帅 袁建 马文倩 荆国林


基金项目:国家科技重大专项(批准号:2016ZX05020?006)资助的课题。
作者简介:韩春杰(1969-),教授,从事钻柱力学的研究。
通讯作者:姜继帅(1998-),硕士研究生,从事深水钻井隔水管相关振动的研究,jishuaijiang243@163.com。
引用本文:韩春杰,姜继帅,袁建,等.深水钻井隔水管横向振动振型分析[J].化工自动化及仪表,2024,51(3):456-461;515.
DOI:10.20030/j.cnki.1000?3932.202403013
摘 要 为了分析深水钻井隔水管的横向振动固有频率和振型,综合考虑深水隔水管受到的顶部张紧力、海洋环境载荷、钻井平台漂移等作用力,借助微元法建立受力分析模型。根据连续梁理论和隔水管单元的动力学微分方程,确定其无阻尼自然振动基本方程,并进一步剖析建立隔水管横向振动固有频率微分方程和模态振型基本方程,然后进行数值求解。使用控制变量法逐步分析隔水管长度、张力比、自身材质对隔水管固有频率的影响和变化规律。通过MATLAB软件表现出不同阶数的振动振型,结果表明:控制张力比、合理选择隔水管类型能够有效提高固有频率,避免与波流力形成共振,进而保证深水钻井作业安全。此外,隔水管的振型并不是标准正弦曲线,振型会受时间的影响不断变化。
关键词 模态振型 深水钻井隔水管 力学分析 固有频率 控制变量法 MATLAB
中图分类号 TE951 文献标志码 A 文章编号 1000?3932(2024)03?0456?07
随着勘探钻井作业进入更深的水域,隔水管设计中的动态振动效应越来越受到关注,因为隔水管的损坏意味着资本损失和昂贵的停机时间。隔水管是井口和平台间的重要设备,在深水海域,隔水管的相對刚度会降低,其固有频率可能会和海流的频率接近,从而发生共振现象。共振状态会使隔水管在横向产生很大幅度的振动,降低隔水管的使用寿命,故存在极大的安全隐
患[1,2]。
准确掌握隔水管的固有振动频率[3,4]和振型是隔水管振动分析和精确设计的基础,动态振动行为中最重要的一部分是由钻井平台自身运动连同隔水管一同形成的,即隔水管的横向自然振动。因此,开展深水钻井隔水管振动特性研究,对于合理选配隔水管和确定相关参数,保证深水钻井作业安全顺利进行具有重要意义。
现阶段对隔水管振动模态振型的深入研究并不多见,文献[5]对隔水管横向自然振动频率以及相关因素对其影响进行了初步研究,但并未考虑时间对模态振型产生的影响。本研究在其基础上重点针对影响因子时间t对模态振型产生的影响进行相关研究,以期找到对应的变化规律。
1 深水钻井系统的力学模型
深水钻井作业条件下,隔水管的受力会比较复杂[6,7]。作用在隔水管系统上的载荷主要包括:
a. 重力,隔水管的重力由其自重和内部的钻井液产生;
b. 浮力,隔水管的浮力由周围的液体和隔水管上分布在各处的浮力块产生;
c. 张紧力,主要由顶部的张紧器产生;
d. 波浪力和海流力,由水质点在波浪中的动态行为产生。
此外,深水隔水管的长度远大于横截面直径,因此在理论计算时常常把隔水管简化为均匀细长的支杆[8]。本研究以隔水管的轴向力方向为x
轴、水平方向为y轴建立深水钻井隔水管力学模型,如图1所示。
2 隔水管横向固有频率的计算
2.1 隔水管横向振动微分方程
使用微元法[9,10],在隔水管上任意部分取一段微元dx,隔水管单位长度受到的浮重为W、弯矩为M、轴向力为F、偏移角为θ、剪切力为Q,受到的海流力与波浪力相结合的力设为F,p、p分别为隔水管管壁外部和内部的压强,示意图如图2所示。
对于隔水管的自然振动来说,固有频率与其本身的结构及边界条件有着极其密切的关系,与外界的载荷无关。根据海洋钻井工程中隔水管单元的动力学微分方程[11],其无阻尼自然振动基本方程可以表示为:
E
I
-T
-m=0(1)
其中,EI为微元的抗弯刚度,对于等截面体,EI=EI;E为隔水管的弹性模量,Pa;I为隔水管的截面惯性矩,m4;T为隔水管的顶部张力,N;m为单位长度隔水管的质量,kg。
式(1)可以写为:
EI-T
-m=0(2)
式(2)属于铰支边界的齐次微分方程,采用分离变量法,设:
y(x,t)=Y(x)T(t)=Y(x)sin(ωt+φ)(3)
其中,φ为偏移角,rad;ω为自然振动的角频率,rad/s。
为便于计算,张力取隔水管所受张力的平均值,T(t)=T,其中:
T=(4)
T=T--++b(5)
其中,d、d分别为隔水管的外径和内径,m;
T、T分别为隔水管顶部张力和隔水管不同长度所受到的张力,N;b为单位长度浮力块产生的浮重,N/m;l为隔水管长度,m;ρ、ρ分别为隔水管密度和钻井液密度。
隔水管单位长度质量的计算式为:
m=(6)
Y(x)简写为Y,这样就可以得到:
EI-T-mωY=0(7)
令ε=,ε=,简化式(7),可得:
-ε-εY=0(8)
当理论分析隔水管横向的自然振动时,设隔水管上部的球形接头与平台相连且平台不漂
移[12],式(8)的边界条件为:
Y|=S
EI
=K
(9)
下边界为:
Y|=0
EI
=
K
(10)
式(8)的特征方程为:
λ-ελ-ε=0 (11)
其中,λ为特征方程的根;K为隔水管顶部挠性接头的转动刚度,kN·m/rad;K为隔水管底部挠性接头的转动刚度,kN·m/rad;S为钻井平台或钻井船横向的漂移距离,m。
特征根有一对实根和一对共轭复根,式(9)、(10)中当K、K取值为0时,微分方程的通解为:
Y=Ce+ Ce+Ccos(λx)+Csin(λx)(12)
λ
=
λ
=-
λ
=
λ
=-(13)
其中,C、C、C、C均為待定系数。
代入边界条件可得:
解得:
C=C=C=0
λ=,n=1,2,3,…
2.2 隔水管横向振动的频谱规律
由理论分析可得:
=(15)
ω=(16)
f=(17)
此处,n表示阶数。
3 隔水管横向自然振动的影响因素分析
结合钻井实例[13],主要参数为:隔水管外径d1=0.5334 m,壁厚0.025 4 m,隔水管长度l=500 m,隔水管密度7 850 kg/m3,钻井液密度1 200 kg/m3,海水密度1 030 kg/m3,隔水管顶部张力T=2.5×106 N。
现采用控制变量法逐一探究隔水管长度、张力比以及隔水管的材质对横向自然振动固有频率的影响。
根据所推的固有频率的相关理论研究,可以证明:
a. 通过表1~3中的数据可以看出,在其他因素不变的情况下,隔水管横向自然振动的固有频率会随着阶数的增加而增大。
b. 根据表1可以看出,同阶数下固有频率会随着隔水管长度的增加而减小,经过理论计算也可得出隔水管达到4 255.29 m时,其第一阶固有频率几乎为0,长度再增加时低阶的固有频率会变为虚数。
c. 表2中,隔水管横向振动的固有频率会随着张力比的增大而增大,并且随着阶数的不断增加,其同阶的变化趋势也随之变大。
d. 相比广泛应用的钢材隔水管以及根据不同海况使用的铝合金隔水管[14],目前已经研制出钛合金钻杆[15]、隔水管等海洋钻探钻井工程中应用的重要部件,结合表3进行分析可以得到,密度4 500 g/cm3的钛合金隔水管要比密度7 000 g/cm3的铝合金以及广泛使用的密度7 850 g/cm3的X80钢材隔水管的横向振动固有频率要高,固有频率越高越能避免与海浪产生的低频形成共振,降低对隔水管的疲劳损耗,延长隔水管的使用寿命。根据表中数据分析可得,张力比及自身材质都是影响隔水管固有频率的重要因素,严格控制才能延长隔水管的使用寿命,降低作业风险。
4 隔水管横向自然振动的模态振型分析
4.1 横向自然振动的模态函数
模态分析[16,17]是确定结构振动特征的一种手段。借助上文推出的隔水管横向自然振动的固有频率,从而可以得到隔水管横向自然振动的模态函数为:
Y(x)=Csin
x=Csin
x(18)
每一阶的模态振型具有相互独立的特性,但是又满足正交条件,即:
mY(x)Y(x)dx=mlδ(19)
δ=1,i=j
0,i≠j(20)
进而可以得到:
Y(x)=sin
x(21)
当隔水管存在顶部张力时,对于n阶含有时间t的模态方程可表示为:
y(x,t)=sin
xsin(ωt+φ)(22)
4.2 振动振型的探究
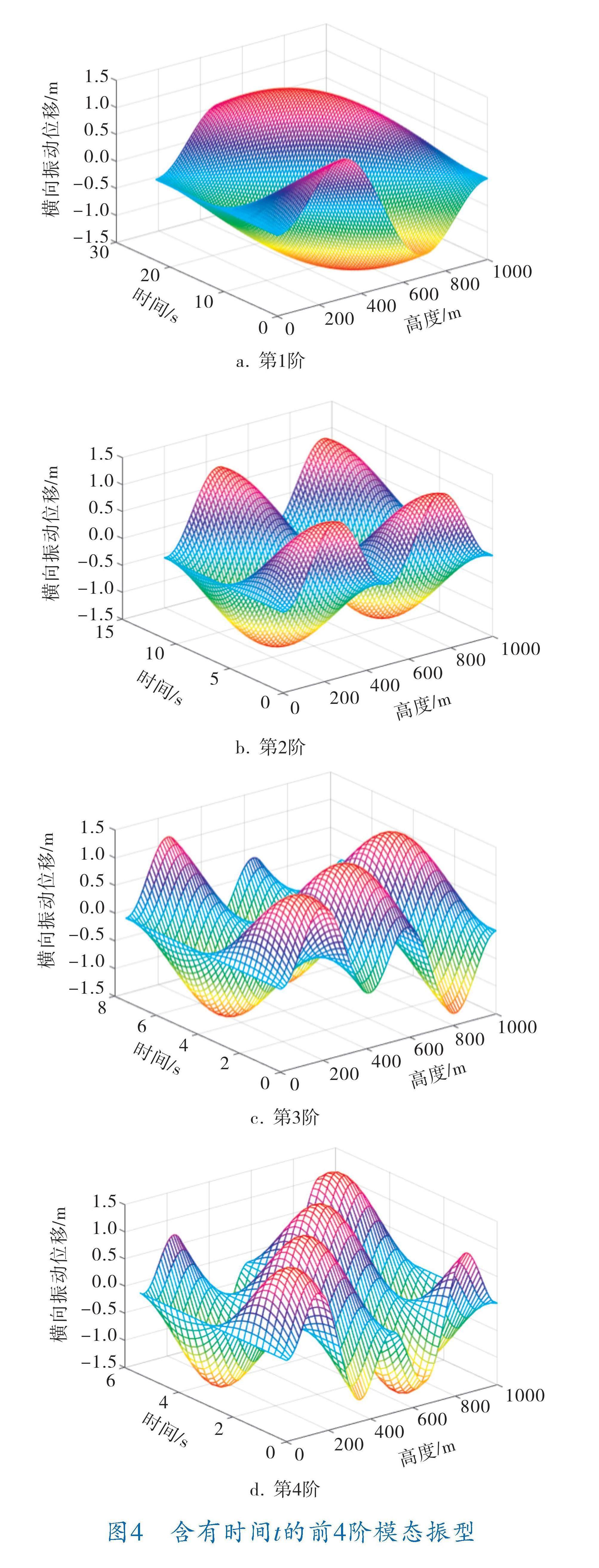
将文献[12]示例中的实际数据代入式(21)、(22),运用软件MATLAB编程计算可以得到隔水管横向振动的模态振型(图3),以及含有影响因子时间t的三维模态振型图(图4)。
根据图3所展现的隔水管横向振动的前4阶模态响应可以看出:第1阶振动响应只有一个节点,横向位移最大值约在0.5l处;第2阶振动响应有两个节点,横向位移最大值约在0.3l和0.6l处;第3阶振动响应有3个节点,横向位移最大值约在0.17l、0.5l及0.83l处;依此类推,隔水管上的最大位移节点会随着阶数的不断增加而遍布整个隔水管的各个部位。
由图4可以看出,隔水管模态振动会产生波动,并且波动数量会随着阶数增加而增多;隔水管的振型会随着时间的变化而不断变化,并且振型不是标准正弦曲线;在时间一定的情况下,波动强度会随着阶数的增加愈发剧烈。
5 结论
5.1 通过所建深水钻井隔水管系统力学模型,使用微元法整合求解得到隔水管横向自然振动基本方程,采用分离变量法求得固有频率,并分析其影响因素可得:固有频率与张力比成正比,与隔水管长度、隔水管密度成反比。
5.2 通过MATLAB软件对求得的横向自然振动的模态函数编程,得出不同阶数的振动振型。分析图像可知:隔水管模态振动波动的数量会随着阶数的增加而增多;在时间一定的情况下,波动强度会随着阶数的增加愈发剧烈;隔水管的振型会随着时间的变化而变化,并且振型不是标准正弦曲线。
参 考 文 献
[1] 陈锟,黄剑,韩雪莹,等.海洋隔水管系统力学特性分析[J].船舶工程,2021,43(12):6-13.
[2] 韩春杰,郭明,王祥旭,等.海洋钻井隔水管横向振动机理的研究[J].化工自动化及仪表,2019,46(12):1028-1031.
[3] 郝逸,王文明,李皓冉,等.基于非线性模型的深水隔水管横向振动固有频率分析[J].石油科学通报,2018,3(3):332-341.
[4] 孙巧雷,李中,王尔钧,等.深水测试管柱与隔水管的横向承载特性[J].天然气工业,2020,40(12):106-115.
[5] 郭明.对深水钻井隔水管振动规律的研究[D].大庆:东北石油大学,2021.
[6] 王川,黎俊,谢真强,等.隔水管悬挂模式下的纵向振动特性仿真研究[J].系统仿真学报,2019,31(10):2122-2130.
[7] 王腾,张修占,朱为全.平台运动下深水钻井隔水管非线性动力响应研究[J].海洋工程,2008(3):21-26.
[8] 李华桂.海洋钻井隔水管的动力分析[J].石油学报,1996(1):122-127.
[9] DAREING D W, HUANG T. Natural Frequencies of Marine Drilling Risers[J].Journal of Petroleum Technology,1976,28(7):61-80.
[10] 董世民,吕庆东,张宁.分布轴向力作用下隔水管横向自由振动分析[J].力学与实践,2016,38(5):538-543.
[11] BURKE B G.An Analysis of Marine Risers for Deep Water[J].Journal of Petroleum Technology,1974,26(4):1-8.
[12] 华勇,钱利勤,吴欣袁,等.深水钻井隔水管与地层管柱耦合力学分析[J].石油机械,2018,46(3):29-34.
[13] 韩春杰,陈明明,闫铁.深水环境下隔水管的横向自由振动分析[J].应用力学学报,2012,29(3):341-344;359.
[14] 韩哲,刘宝昌,周海龙,等.深水钻井铝合金隔水管材料腐蚀疲劳试验研究[C]//第二十届全国探矿工程(岩土钻掘工程)学术交流年会论文集.北京,2019:416-422.
[15] 吴欣袁,张恒,徐学军,等.钛合金在石油天然气勘探开发中的应用[J].石油化工应用,2016,35(11):105-108;113.
[16] JIN Y,AKOREDE A F.Modal analysis of deep?water drilling riser in freestanding disconnected mode[J].
Ocean Engineering,2022(4):260-299.
[17] GAO G H,CUI Y J,QIU X Q,et al.Study on Natural Vibration Frequency and Mode Shape of Deep Sea Top Tensioned Riser[J].Journal of Physics:Conference Series,2018(5):22-36.
(收稿日期:2023-03-07,修回日期:2024-04-16)
Analysis of Transverse Vibration Mode of Deep?water Drilling Riser
HAN Chun?jie1a, JIANG Ji?shuai1a,2, YUAN Jian1a, MA Wen?qian1a, JING Guo?lin1b
(1a. School of Physics and Electronic Engineering ;1b. College of Chemistry and Chemical Engineering,
Northeast Petroleum University; 2. Shandong Huayu University of Technology )
Abstract For purpose of analyzing both natural frequency and mode of transverse vibration of the deep?water drilling riser, many forces such as the top tension force, marine environment load and the drift of drilling platform were comprehensively considered and their force analysis model was established based on the infinitesimal method. Through basing on continuous beam theory and the dynamic differential equation of the drilling
(Continued on Page 515)
