基于改进动态核主元分析算法的化工过程故障检测
2024-06-07赵鹏洪悦
赵鹏 洪悦

基金项目:辽宁省教育厅2021年度科学研究经费面上项目(批准号:LJKZ0460)资助的课题。
作者简介:赵鹏(1997-),硕士研究生,从事边缘计算的故障检测的研究,1184470646@qq.com。
引用本文:赵鹏,洪悦.基于改进动态核主元分析算法的化工过程故障检测[J].化工自动化及仪表,2024,51(3):403-409.
DOI:10.20030/j.cnki.1000?3932.202403005
摘 要 为克服工业过程数据的非线性、动态性等限制,提出基于希尔伯特黄变换的动态核主元分析算法(HHT?DKPCA)。首先用标准化正常数据计算均值和标准差,之后对原始数据进行标准化。然后对协方差矩阵进行特征分解,将数据映射到低维空间。HHT变换去噪前对每个主元变量进行降维,然后将去噪后的数据重新映射到高维空间,并重新计算T2和SPE。将HHT?DKPCA与PCA、KPCA、DKPCA、HHT?PCA在TE过程故障数据上的处理结果进行比较,结果表明,HHT?DKPCA具有更高的故障检测率。
关键词 故障检测 动态核主元分析 HHT变换 TE过程
中图分类号 TP277 文献标志码 A 文章编号 1000?3932(2024)03?0403?07
在工业过程故障诊断领域,由于基于数据驱动的故障检测和诊断方法无需准确的模型,只需对工业生产过程采集的数据进行数学分析即可实现故障检测,因此近年来得到了广泛应用[1~3]。
工业生产数据往往存在动态性、非线性、高维及样本容量大等特点。为了方便计算,需对数据进行处理,常用的方法以主元分析(Principal Component Analysis,PCA)方法为主,但PCA[4]对非线性数据的处理效果并不好。为了提高非线性数据的处理效率,提出了核主元分析(Kernel Principal Component Analysis,KPCA)方法。KPCA[5]的原
理是使用非线性核函数将原始输入数据映射到高维特征空间,并在该空间中计算核矩阵的特征值和特征向量。但是KPCA在处理动态数据时容易遗漏数据,所以在此基础上提出动态核主元分析(Dynamic Kernel Principal Component Analysis,DKPCA),该方法通过在原始数据矩阵中加入动态时滞矩阵来构建增广矩阵,然后利用核函数将非线性低维数据映射到高维线性空间,最后在高维特征空间中进行主元分析。
针对工业生产过程中存在的多模态、方差差异明显和非高斯特性,郭金玉等提出了一种故障检测方法——加权局部近邻标准化PCA方法[6],在标准化后的数据上建立PCA模型,使用SPE和T2统计量进行故障监视。针对原始信号中噪声信号会干扰齿轮故障模式识别这一问题,高庆云等提出了一种以CSAEMD?KECA角结构距离为基础的齿轮故障识别方法[7],利用角结构距离的聚类算法对特征数据集进行聚类分析,准确率高达98.3%。翟坤等提出了一种新的基于KPCA的非线性过程监测技术[8],与其他非线性PCA[9]技术相比,KPCA只需要求解特征值问题,不需要任何非线性优化;同时还提出了一种在特征空间中计算平方预测误差SPE的简单方法,与线性PCA相比,该技术表示出了优越的过程监控性能。
为了解决工业生产数据的动态性、非线性等问题,笔者在DKPCA的基础上进行改进,提出HHT?DKPCA方法,对每个主元变量进行降维、采用HHT变换对数据进行降噪,通过增加核函数和增广矩阵,消除数据时序间的相关性,从而实现对动态过程的故障检测,提高故障检测正确率。
1 HHT?DKPCA算法
1.1 DKPCA
DKPCA[10~12]的主要思想是在原始数据矩阵中加入动态时滞矩阵来构建增广矩阵,然后利用核函数将非线性低维数据映射到高维线性空间,最后在高维特征空间中进行主元分析。简而言之,DKPCA采用了一种非线性到线性的转换方法,通过提取特征向量的动态自相关性来处理非线性问题。
时间序列模型如下:
X(a)=[X(a)T,X(a-1)T,…,X(a-d)T](1)
其中,X(a)为a时刻训练样本的观测值;d表示动态矩阵的延迟;下标i表示当前向量属于时间序列。
构造动态时滞矩阵如下:
X=
x(a)
x(a-1) …
x(a-d)
x(a-1)
x(a-2) …
x(a-d-1)
[…] […] ? […]
x
[a-(
a-d)]
x[a-(
a-d)-1]…
x(
a-a)(2)
其中,数据x(a)∈R(a=1,2,…,n),n表示样本个数,m表示空间维度。
特征空间中的协方差矩阵C的特征方程为:
λv=Cv(3)
其中,λ是协方差矩阵中的非零特征值;v是特征向量。
?()表示内积核函数,映射过程中去均值处理,则协方差矩阵可表示为:
Cv=?(x)?(x)(4)
式(4)用核矩阵表示为:
[K]=K=〈?(x),?(x)〉(5)
其中,K为n×n的核矩阵,K表示?(x)与?(x)的点积。
式(5)简化后可得:
nλp=Kp,p=[p,…,p](6)
其中,p为映射空间中的相关系数,nλ为K的特征值。
不同情况下选用不同的核函数,文中使用高斯径向基核函数构造核函数[13,14]:
K=exp
(7)
其中,‖x-y‖2为两个特征向量之间的距离,σ为核函数的参数。对复杂的高维空间进行均值中心化处理:
K=K-IK-KI+IKI(8)
其中,I表示元素为1/n的l×l方阵,K表示均值中心化处理后的核矩阵。
因此,对于DKPCA[15],特征空间中的主元分析转换成对核矩阵的特征值分解问题,具体表示如下:
t=〈v,?(x)〉=a〈?(x),?(x)〉=aK(x,x)(9)
其中,t为映射?()在特征向量v上投影的第k个核主元向量,a为规范化系数向量。
1.2 HHT?DKPCA故障检测方法
首先,使用初始数据建立PCA主成分模型,将初始数据映射到低维空间,使用HHT[15,16]算法去噪。然后,将去噪后的数据重新映射到高维空间,更新主成分模型。通过两步递推法,可以获得扩展矩阵的分块主成分模型。接着,对合并的分块主成分模型再次进行主成分分析。对于待检测数据,可以构造扩展矩阵。扩展矩阵的每个块可以通过对应块的主成分模型进行降维处理,然后通过合并的主成分模型再次降维处理,最后实现故障检测。
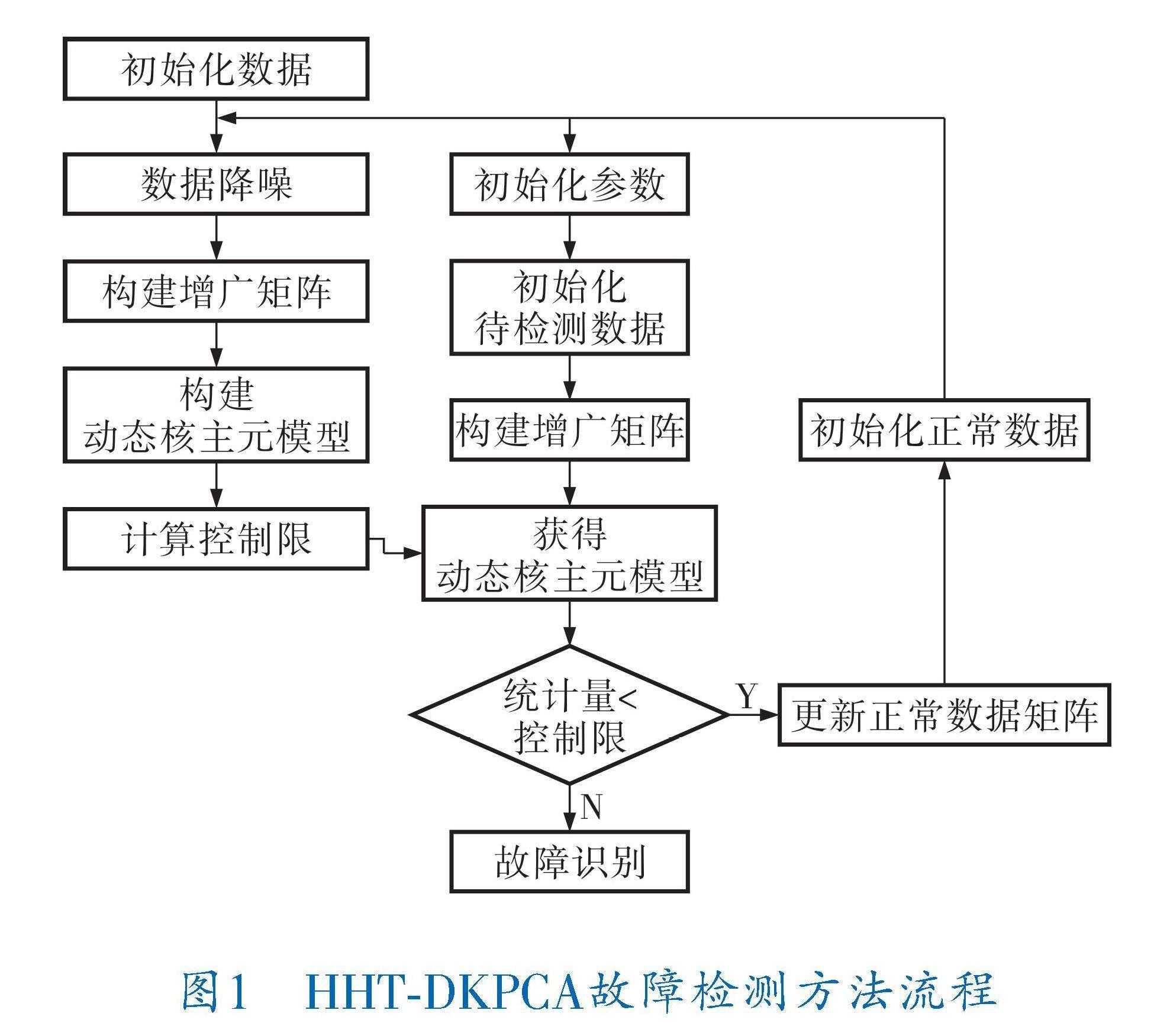
HHT?DKPCA故障检测方法实现流程(图1)如下:
a. 对正常数据进行标准化,使用均值和标准差来标准化原始数据;
b. 对协方差矩阵进行特征值分解;
c. 将数据映射到低维空间中,并对低维空间的每个主元变量进行HHT变换去噪处理;
d. 将去噪后的低维空间数据重新映射到高维空间中;
e. 更新主元模型并计算控制限的T2统计量和SPE统计量;
f. 收集新数据,并使用正常数据的均值和标准差对其进行初始化;
g. 利用新的主元模型计算待检测数据的T2统计量和SPE统计量;
h. 比较待检测数据的T2统计量和SPE统计量与对应的控制限;
i. 如果超过控制限,则认为故障,并使用残差贡献图进行故障识别,然后返回步骤f;
j. 如果未超过控制限,则被识别为正常数据,删除最早数据,然后返回步骤a。
2 实验仿真
2.1 过程故障与数据
TE过程数据分为训练集和测试集,两者分别有21种故障数据,测试集共含有960个数据,其中前160个观测值为正常数据。本实验采用前20个故障数据进行实验研究。在这些故障中,前15个故障类型是已知的,最后5个故障类型是未知的。故障1~7的误差干扰类型为阶跃变化,例如改变A/C的进给速度;故障8~12的误差干扰类型为随机变化,例如反应釜冷却水进水温度;故障13的干扰类型为缓慢漂移,例如电抗器动能效率下降;故障14、15的干扰类型为阻塞,例如电抗器或电容器冷却水进水口调节阀的阻塞;故障16~20的干扰类型未知。
控制限是一种用于确定数据是否异常的统计方法。通常,控制限是根据数据的均值和标准差计算得出的。在TE数据中,可以通过计算控制限来确定正常数据和异常数据的范围。如果前160个数据中低于控制限的变量数越多,则T2和SPE的漏报率越低,效果越好。这意味着油气生产数据的正常数据点被正确地分类为正常数据点,而没有被误认为是故障数据点。在第161~900个数据中,高于控制限的数据越多越好。这是因为这些数据都是故障数据,因此需要尽可能多地识别这些数据,并将其标记为异常数据。如果出现低于控制限的数据,则表明故障检测率下降。
2.2 仿真结果与分析
由表1可知,各种方法对于不同故障类型的处理效果差异显著。一些故障类型在某些方法下表现出高准确率(接近或达到100%),而在其他方法下則较低。这表明不同的故障类型具有不同的特性,需要针对性地选择合适的处理方法。
PCA与KPCA对比。PCA是一种线性降维方法,而KPCA通过引入核函数,能够处理非线性问题。从数据中可以看到,对于某些故障类型(如故障类型3、5、9等),KPCA的效果明显好于PCA,表明这些故障类型的数据具有非线性特性。
DKPCA与KPCA对比。DKPCA是KPCA的扩展,旨在进一步提高性能。从数据上看,DKPCA在多数故障类型下都略优于KPCA,尤其在故障类型3、5、9、10等上优势明显。
HHT与PCA、DKPCA结合后进行对比。HHT是一种时频分析方法,与PCA或DKPCA结合可以进一步提取数据的特征。从数据上看,HHT?PCA和HHT?DKPCA在多数故障类型下都表现较好,尤其是HHT?DKPCA在多个故障类型中都达到了或接近100%的准确率。
由于TE数据中故障11和故障20的样本特征比较明显,具有明显的非线性、动态性,因此笔者重点选择这两个故障数据进行算法仿真分析。
由图2和表2、3可以看出,传统的主元分析方法,如PCA、KPCA和HHT?PCA的检测率都偏低,因此这3种方法不适用于该数据集。DKPCA和HHT?DKPCA均具有较高的检测率,但DKPCA的误报率偏高。而且对于统计量T2,HHT?DKPCA的检测率明显高于DKPCA。所以总体上来讲,HHT?DKPCA算法优于其他算法,具有更好的检测性能。
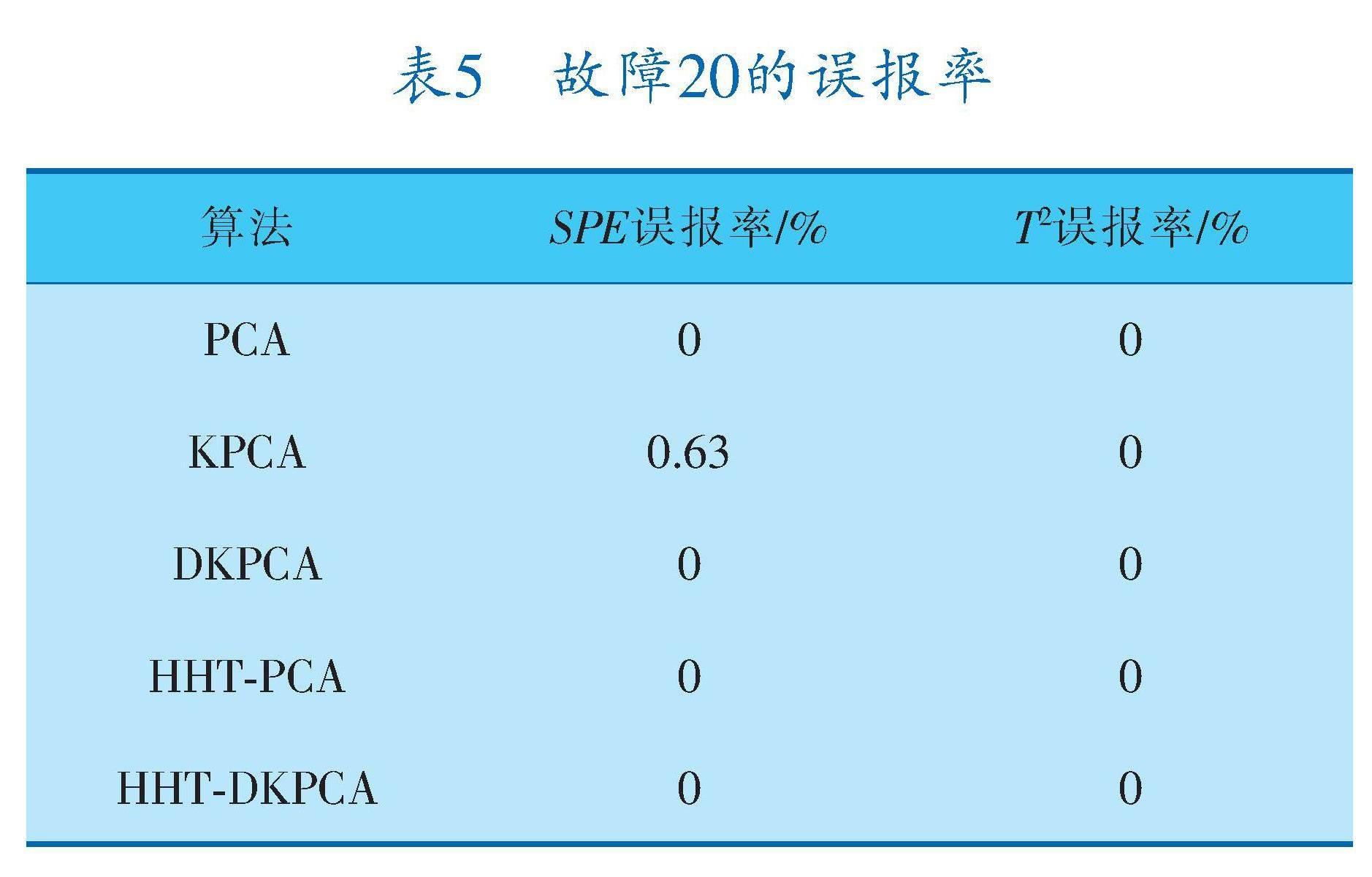
由图3和表4、5可以看出,各算法对故障20的误报率几乎为零,说明这个数据集中故障点的标记是正确的,适用于以上几类算法。然而传统PCA算法与HHT?PCA算法的检测率明显低于其他3种算法,说明这种数据以非线性数据为主,而PCA算法无法处理非线性数据,因此效果不如其他方法。HHT?DKPCA算法对数据降噪处理后的检测效果稍微有所提升,但是提升幅度不明显。综合来看,该数据集中HHT?DKPCA算法相对于其他算法的优势不明显但有小幅提升。
3 结束语
筆者对TE过程数据进行处理和分析,以T2和SPE统计量为基础,运用PCA、KPCA、DKPCA、HHT?PCA和HHT?DKPCA进行了故障检测。重点选择故障11、20两类强类型样本进行仿真和检测率分析,实验结果表明,HHT?DKPCA对于两类样本的数据特征都有着不错的效果,表明HHT?DKPCA更加适用于TE过程数据的故障检测。PCA、KPCA可以有效降低数据维度,去除数据中的冗余信息和噪声,从而提高故障检测的准确性和效率。DKPCA、HHT?PCA则更加适合处理非线性和非平稳的信号数据,并且能够更好地捕捉信号中的变化和趋势。
参 考 文 献
[1] 黄涛,王颖,周艳芳,等.基于数据驱动的微电网故障检测方法[J].中国计量大学学报,2021,32(1):46-53.
[2] CHEN H T,CHAI Z,JIANG B,et al.Data?Driven Fault Detection for Dynamic Systems with Performance Degradation:A Unified Transfer Learning Framework[J].IEEE Transactions on Instrumentation and Measurement,2021,70.DOI:10.1109/TIM.2020.3033943.
[3] ZHANG C,GUO Q X,LI Y.Fault detection method based on principal component difference associated with DPCA[J].Journal of Chemometrics,2019,33(1):e3082.
[4] 李元,张轶男.基于双局部近邻标准化与主多项式分析的故障检测方法[J].计算机应用与软件,2022,39(8):273-279;319.
[5] 郭金玉,于欢,李元.基于KPCA?SVM的相关和独立变量故障检测方法[J].深圳大学学报(理工版),2023,40(1):14-21.
[6] 郭金玉,李涛,李元.基于主元增广矩阵的SVM故障检测[J].深圳大学学报(理工版),2021,38(5):543-550.
[7] 高庆云,郭力,陈长华.基于CSAEMD?KECA和角结构距离的齿轮故障识别方法[J].机电工程,2023,40(1):11-22.
[8] 翟坤,杜文霞,吕锋,等.一种改进的动态核主元分析故障检测方法[J].化工学报,2019,70(2):716-722.
[9] ZHAO Y P,HUANG G,HU Q K,et al.An improved weighted one class support vector machine for turboshaft engine fault detection[J].Engineering Applications of Artificial Intelligence,2020,94:103796.
[10] 张成,韩宏宇,李元.去主元相关性DKPCA故障检测与诊断方法[J].计算机技术与发展,2023,33(4):161-167.
[11] ZHU M R,JI Y J,ZHU X Y,et al.Energy consumption mode identification and monitoring method of process industry system under unstable working conditions[J]. Advanced Engineering Informatics,2023,
55:1-18.
[12] ZHANG J X,LUO W J,DAI Y Y,et al.Cycle temporal algorithm?based multivariate statistical methods for fault diagnosis in chemical processes[J].中国化学工程学报(英文版),2022(7):54-70.
[13] ZHANG Q,LI P,LANG X,et al.Distributed process monitoring for large?scale processes based on MJMI?weighted DKPCA[J].The Canadian Journal of Chemical Engineering,2022,100(10):12-17.
[14] 陆孝锋,李鹏,高莲,等.基于DKPCA的电力信息系统虚假数据注入攻击检测方法[J].电子测量技术,2022,45(2):91-97.
[15] TRUNG NGUYEN THANH,HUNG NGUYEN HUU,CHI THAI THI KIM,et al.Detection of the instantaneous frequency degradation due to damages of a fixed offshore jacket platform using the iEEMD?based Hilbert Huang Transform under a wave excitation[J].Structural Control and Health Monitoring,2022,29(12):1-23.
[16] LU Z Q.Review on mechano?electronic device fault diagnosis based on Hilbert?Huang Transformation[J].Journal of Physics:Conference Series,2022,2351(1):47-52.
(收稿日期:2023-05-24,修回日期:2024-04-10)
Fault Detection of Chemical Process Based on Improved Dynamic
Kernel Principal Component Analysis Algorithm
ZHAO Peng, HONG Yue
(School of Information Engineering, Shenyang University of Chemical Technology)
Abstract For purpose of overcoming the nonlinear dynamics limitations of industrial process data, a Hilbert?Huang transform?based dynamic kernel principal component analysis algorithm (HHT?DKPCA)was proposed, in which, having the standardized normal data based to calculate both mean value and standard deviation and then the original data standardized, including having the covariance matrix decomposed and the data mapped to the low?dimensional space. For each principal component variable, having the dimension reduction performed before Hilbert?Huang transform de?noising, and then, having the data de?noised remapped to high?dimensional space and both T2 and SPE recalculated. Comparing the results of HHT?DKPCA with PCA, KPCA, DKPCA and HHT?PCA in TE process data set shows that, the HHT?DKPCA has higher fault detection rate.
Key words fault detection,DKPCA, HHT,TE process
