基于调查分析 关注推理意识
——学生解决 “∠1和∠2是否相等” 问题的调查与教学启示
2024-06-04□何洁
□何 洁
一、问题的提出
某区四年级上册的质量检测卷中,出现了这样一道题目(如图1)。
本题不仅要求学生准确判断两个角是否相等,还要求他们说明判断的理由。这样的题目,有多少学生能够正确作出判断?学生会从哪些角度入手说明理由?对于那些无法正确说明理由的学生,他们面临的具体困难是什么?带着这一系列问题,笔者开展了调查与分析,从而准确把握学生说理的角度,为教师实施精准教学提供参考。
二、分析与结果
笔者在所在学校四年级中,选取不同教师执教的三个班级共130名学生展开测评。对回收的130份试卷进行深入分析后,得出以下结论。
(一)超过九成的学生判断∠1和∠2相等
统计结果显示,有119 名学生认为∠1 和∠2 相等,占总人数的91.54%。这表明在四年级学生中,有超过九成的学生能够正确判断这两个角相等。而余下的11 名学生(占总人数的8.46%)受各种因素影响,认为∠1和∠2不相等。
(二)学生主要从 “看” “量” 以及 “论证” 这三个角度说明理由
学生会从哪些角度入手说明理由,会如何表达说理的过程,是评价中的一项重要内容,也是实施精准教学的前提。通过对130份试卷的分析,笔者发现:学生主要从 “看” “量” 以及 “论证” 这三个角度入手说明理由。
1. “看” 的角度
“看” 是指观察题目给出的示意图,通过目测,判断∠1 和∠2 的大小关系。采用这种方法的学生共有18 人,占总人数的13.85%。从 “看” 的角度说理可分成两种情况。
一是借助 “第三个量” 判断两角相等。这里的 “第三个量” 指的是与∠1和∠2都相等的量。例如,有学生利用 “看起来∠1和∠2都是90°的一半” 这一观察结果,得出∠1=∠2 的结论。这里的 “90°的一半” 就是 “第三个量” 。部分学生为了进一步验证 “看” 的结果的合理性,还运用算式计算出角的度数,从而证明两角相等。具体来说,学生是先看出∠1和∠2都是45°,再通过算式90°÷2=45°来 “有力” 说明∠1和∠2两角的确是相等的。
二是通过 “移动重合” 判断两角相等。 “移动重合” 是指将∠1或∠2进行移动,看它们是否重合,从而得出结论。例如,有学生写着: “相等,因为把阴影部分向下移,∠1和∠2是重合的。” 还有学生的理由是: “因为它们(指∠1和∠2)可以重叠在一起。” 这部分学生是运用长方形纸片进行实际操作得出结论的,还是没有操作通过想象得出结论的呢?访谈发现,这些学生是在头脑中利用表象通过想象旋转∠1或∠2使两角重合,进而判断两角相等。
2. “量” 的角度
“量” 是指学生通过使用量角器测量出∠1和∠2的度数来判断它们是否相等的结论。采用这种方法的学生仅有3 名,占总人数的2.31%。其中两名学生测量得到的结果是∠1与∠2相等,而另一名学生因为测量时的误差,得到不相等的结果。
3. “论证” 的角度
“论证” 是指学生运用已知条件,有根有据地进行推理,从而得到∠1和∠2相等。采用这种方法的学生占总人数的36.92%。说理过程主要有以下两种形式。
第一种是利用 “两角之和相等” 进行论证。这些学生先将∠1和∠2之间的角命名为∠3,并在图上标注出来(如图2)。然后利用∠1 与∠3、∠2 与∠3 “两角之和” 都是90°这一事实得出结论。即:因为∠1+∠3=90°,∠2+∠3=90°,所以∠1=∠2。虽然四年级学生尚未学过 “等式的性质” 或 “余角的性质” ,但仍有35 名学生(占总人数的26.92%)采用 “两角之和” 的思路来论证。

图2
第二种是利用 “两角之差相等” 进行论证。学生同样先将∠1和∠2之间的角命名为∠3,在图上标注出来。然后利用∠1=90°-∠3、∠2=90°-∠3,得出∠1=∠2的结论。这种论证思路与 “两角之和” 的论证思路类似,但更直接地运用了 “等量的等量相等” 这一原理,共有13 名学生(占总人数的10.00%)采用这种思路。
(三)学生遇到的主要困难是 “不知道度数” 和 “不知道怎么说明理由”
针对学生在解题过程中遇到的困难,笔者也展开了调查。调查结果显示,在130 名学生中,有70名学生表示未遇到困难或未书写困难,另外60 名学生则详细描述了他们在解题过程中遇到的困难。其中, “不知道度数” 和 “不知道怎么说明理由” 是学生遇到的主要困难。
1.不知道度数
“不知道度数” 是指学生不知道∠1、∠2和∠3的度数,所以无法判断两角相等。学生的描述有: “不清楚∠1 和∠2 是多少度。” “不知道∠3 是多少度,所以不能确认∠1 到底等不等于∠2。” “不知道旋转的度数,没有确切的度数,不好算。” 在60名详细描述遇到的困难的学生中,有31名学生表达了这种 “不知道度数” 的困惑。这些学生认为,判断两个角的大小首先要知道它们各是多少度。
2.不知道怎么说明理由
“不知道怎么说明理由” 是指学生不知道怎么来表达∠1 和∠2 相等或不相等的理由。学生的描述有: “不知道怎样详细说明理由。” “想到了却写不出来,不知道怎么表达。” “没有办法清楚直观地写出自己想要表达的观点。” 在60名详细描述遇到的困难的学生中,有13名学生表达了诸如 “不知道怎么说明理由” 的困惑。事实上,四年级学生在之前的学习经历中确实较少遇到这样需要写出说理过程的问题,所以他们不知道怎么说明理由也在情理之中。
三、教学实施
经过上述深入细致的调查与分析,笔者已经较为清晰地掌握了学生在判断两个角是否相等问题上的正确率。同时,也明确了学生会从哪些角度说理以及如何说理,知道了他们在解决这个问题时遇到的主要困难是什么。基于这些信息,笔者设计了更加精准的教学过程,以确保教学目标的顺利实现。
(一)教学过程
1.让学生独立思考并解决这个问题,为小组交流做准备
(1)根据你的判断,∠1和∠2相等吗?
(2)你的理由是什么?
这个环节主要是让学生对相关内容进行回顾与梳理,重点准备在小组交流中怎么说。
2.学生以四人小组为单位,分别在小组中说一说自己的结论与理由
根据前期调查,预计有超过三分之一的学生会采用 “论证” 的方法。本环节旨在让学生通过交流了解不同的说理方式,学习如何运用已知的条件有根有据地讲道理,即运用论证的方法说理。
3.要求学生做好在全班交流的准备
(1)你们小组有没有形成统一的结论?
(2)你们小组采用了哪几种说理的方法?
(3)你们小组认为哪一种说理的方法是比较可靠的,为什么?然后推荐一名同学为小组代表,向全班汇报。
从前面的调查分析中可知,学生主要采用 “看” “量” 以及 “论证” 的方法进行说理。所以在一个小组中,有可能会出现两种或两种以上的说理方法,因此,本环节要求学生对几种说理方法进行初步比较,以便在全班交流,让学生通过生生交流和师生交流提升说理的严密性。
4.全班交流
先由一名小组代表发言,汇报准备的内容,其他小组进行补充。然后在教师的引导下,归纳出 “看” “量” 与 “论证” 三种说理方法。接着,通过实物操作与课件动态演示,引导学生观察长方形的旋转过程,看到两个长方形完全重合。最后,让学生比较三种说理方法的可靠性,体会论证方法的严密性,从而得出以下结论。
(1)观察∠1 和∠2 是否相等的确重要,但仅凭观察得出的结论是不可靠的。即使先观察到∠1和∠2 都是直角的一半,再用算式算出∠1 和∠2 都等于45°,这样的说理方法仍然不可靠。
(2)量的方法相对可靠,但存在误差。不同的人或同一个人多次测量同一角度,可能会得到不同的结果。比如,可能一个人量出来都是45°,说∠1与∠2 相等,而另一个人量出∠1 与∠2 相差1°,说两角不相等。因此,仅凭量的结果判断∠1与∠2是否相等也没有那么可靠。
(3)运用已知条件有根有据地说理论证是最可靠的方法。题目要求判断 “∠1和∠2是否相等” ,因此需先寻找∠1(或∠2)与已知条件之间的关系,再进行说理。已知长方形的角是直角(90°),∠1和∠2都比直角(90°)要小,且∠1(或∠2)与两个角之间未标注的角(学生将其命名为∠3)之和正好等于直角。基于这一发现,学生可以得到:∠1+∠3=90°和∠2+∠3=90°。由于两个等式中都有∠3,因而可以得出∠1=∠2的结论。另一种表达方式是:∠1=90°-∠3,∠2=90°-∠3,得出∠1=∠2。总之,无论使用 “和相等” 还是 “差相等” 的方式来说理论证,其思路都是类似的,都是基于已知条件和数学原理进行严谨推导的过程。
5.回顾与小结(略)
(二)后测的试题、结果与分析
上述教学过程是否真正促进了学生的发展?是否有效帮助更多学生掌握论证的方法?这样教学后,学生是否学会了迁移应用?为了验证这些猜测,笔者对学生进行了后测。以下是后测试题、所得结果以及对结果的简要分析。
1.后测试题
原来的后测试卷是在试卷中增加了以下三道题。
(1)下图(如图3)由直角三角形ABC旋转而成。图中∠4与∠5相等吗?请说明理由。
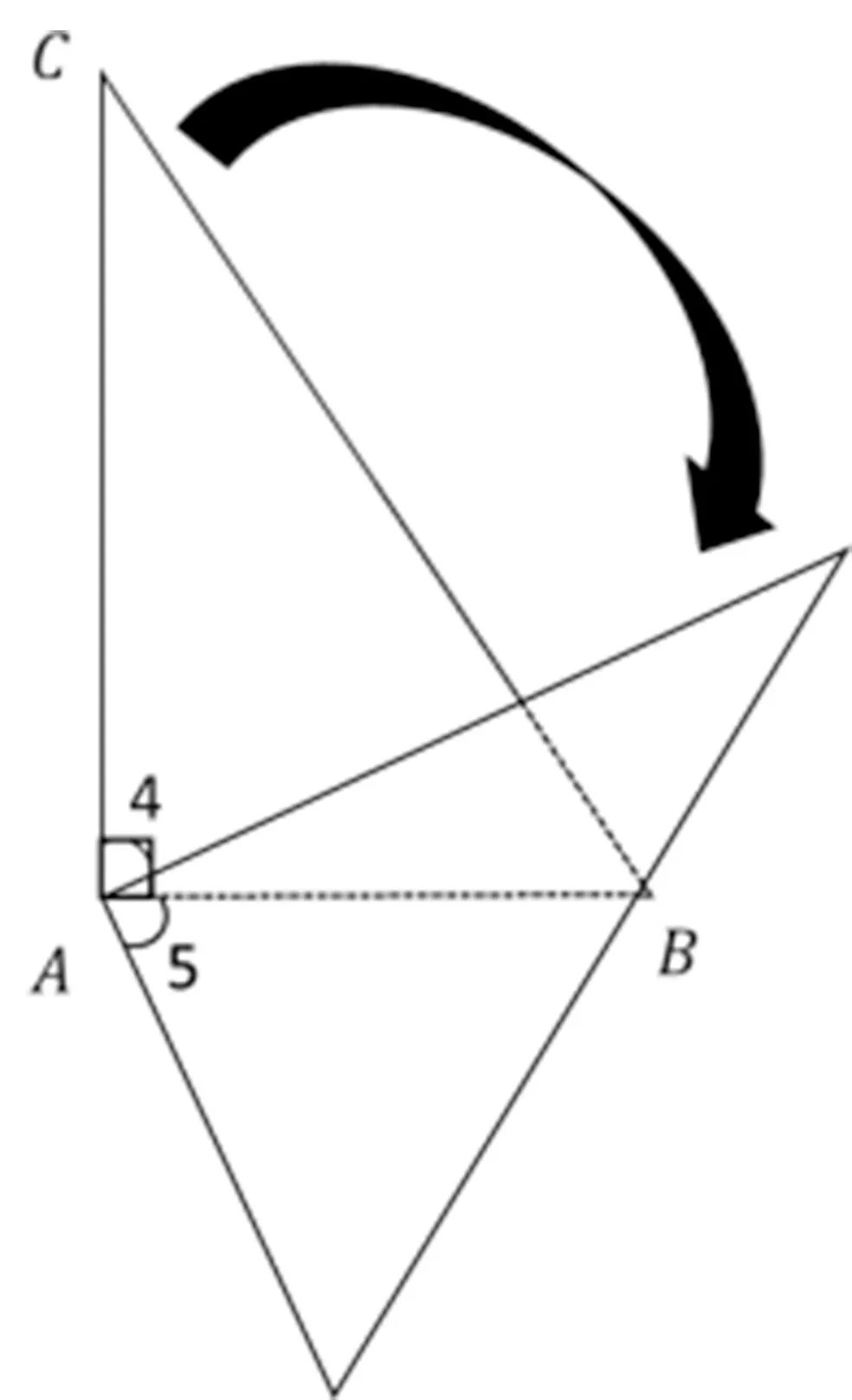
图3
(2)下图(如图4)由三角形ABC旋转而成。图中∠6与∠7相等吗?请说明理由。
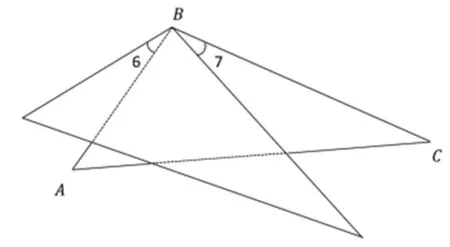
图4
(3)下图(如图5)是一个长方形ABCD绕点A旋转的示意图。观察它的旋转过程,你发现了什么?写一写。
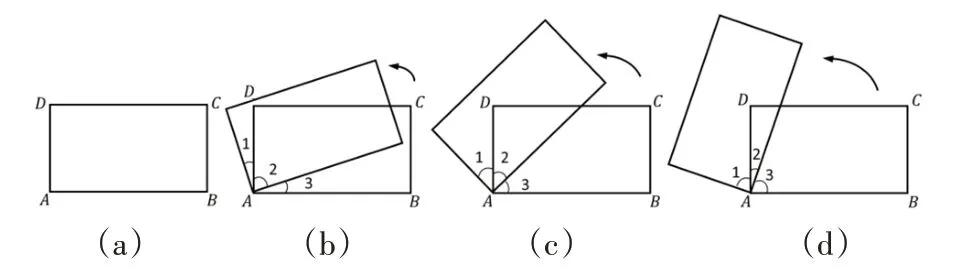
图5
2.测试结果
共有130名学生参与后测,新增三题的测试情况如表1所示。
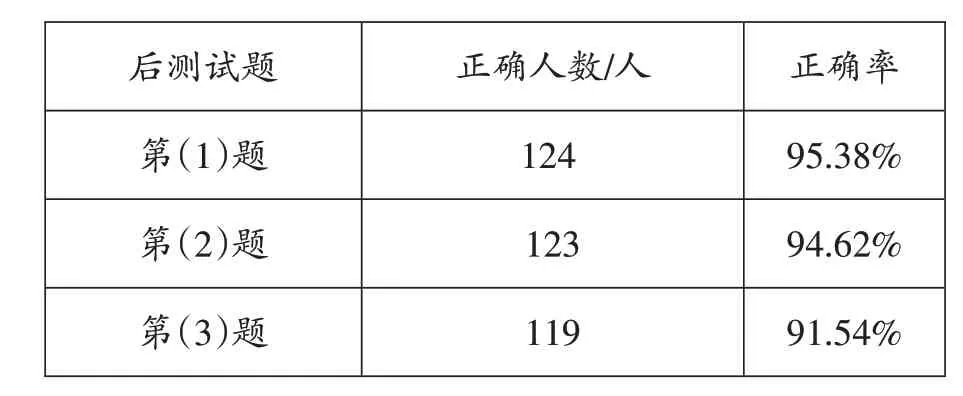
表1
3.结果分析
从所得数据可以看出,经过这样的教学过程,学生采用论证方法说理的正确率从原来的36.92%提升至90%以上。特别是第(1)题和第(2)题,超过90%的学生成功迁移了解决问题的方法。此外,进一步对第(3)题进行分析,发现有超过70%的学生发现了 “不管在什么情况下(怎么旋转),∠1 和∠3的度数始终保持一致(因为∠1+∠2=90°,∠3+∠2=90°)” 的规律。
四、研究启示与建议
(一)学生习惯用 “具体的数或数的运算” 说理,不习惯用抽象的符号说理
通过上面的调查与分析可知,为了说明∠1=∠2,学生希望知道它们各是多少度,或者用算式计算出它们的具体度数来说明这两个角相等,而不习惯用 “等量的等量相等” 这样的原理以及抽象的符号说理。如图6所示,学生在得出 “∠1=90°-∠3,∠2=90°-∠3” 后,并未立即意识到∠1=∠2,而是继续计算两角的具体度数,直至得出 “40°=40°” 的结论,才确认两角相等。这表明学生在没有具体数值支撑的情况下,对结论的可靠性存在疑虑。只有当他们通过测量或观察得出具体度数,并通过计算验证两角度数相等后,才会对结论感到 “安全” 。
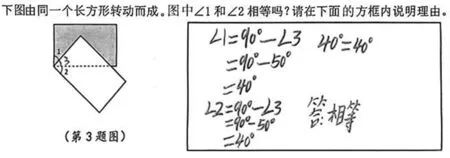
图6
(二)对学生认知水平的评价不仅要关注结果的正确性,也要关注过程表达的逻辑性
根据调查统计,虽然超过90%的学生能够正确判断∠1和∠2相等,但能够清晰说明理由的学生比例却不足60%。这意味着在认知过程中有超过30%的学生存在说理障碍。若仅依据结果进行判断,就无法全面了解这部分学生的真实认知水平。例如,学生甲仅凭观察就得出了∠1 和∠2 相等,而学生乙在观察后还用量角器进行了测量,结果由于测量的误差,得出了∠1和∠2不相等的结论。如果只看结果,容易误认为学生甲比学生乙的认知水平高。而事实上,学生乙的认知水平是高于学生甲的。因此,在评价学生的认知水平时,必须同时关注结果的正确性和过程表达的逻辑性。
(三)从调查入手,仔细分析学生的认知现状是实施精准教学的前提
上述调查与分析帮助教师了解了学生的真实起点和需求,使教师对学生的认知现状有了更为清晰的认识,这为他们后续实施精准教学提供了有力的支撑和依据。从后测结果可知,四年级学生已经具备推理的能力。只要教师的引导方法得当,学生就能够达到 “有根有据、有条有理” 的说理水平。
