基于粒子群优化算法的储能电站经济性优化方法研究

中电建华东勘测设计院（深圳）有限公司 张学昶

随着新能源技术的不断发展，电力系统中新能源并网容量不断增加，这使得储能技术在电力系统的应用中越来越重要。储能电站在电力系统稳定运行、优化资源配置、提高能源利用效率等方面发挥着重要作用。然而，在储能电站建设之前，需要对储能电站的经济性进行分析，以确保其建设具有较高的经济效益[1]。本文旨在介绍一种基于粒子群优化算法的储能电站经济性优化方法，以提高储能电站的经济性。

在实际工程应用中，储能电站的经济性会受到安装以及维护运行等成本影响，因而需要综合考虑其经济性并采用最优方案。本文主要研究如何根据实际中的典型应用场景，建立储能电站在配网侧的经济性价值评估模型，并利用粒子群优化算法来确定储能系统充放电控制经济性最优策略。

1 储能电站的研究现状

蓄电池储能技术的日益成熟与广泛应用，正逐步攻克风电、光伏发电等新能源接入与消纳所面临的技术难题，缓解电网因需求波动而产生的调峰压力，降低投资建设配套输电线路容量的需求[2]。

目前，各种储能蓄电池技术中，铅酸蓄电池由于历史悠久、技术成熟且成本较低而被广泛应用，但由于其能量密度有限、使用寿命短以及可能引发的环境问题，使得铅酸蓄电池在实际应用中的推广逐渐受阻。镍镉电池在动力电池领域的应用以达到一定的普及度，然而因其所带来的重金属污染问题日益突出，使得更为环保的镍氢电池逐渐取代其地位。与此同时，锂电池因受限于大规模集成技术的复杂性，始终未能在大容量应用方面取得突破[3-4]。

新兴钠硫电池和液流电池技术日益受到人们的瞩目，并在实际应用中逐渐占据一席之地。钠硫电池因具有高能量密度、高效率、环保性以及大容量等诸多引人注目的特点，被视为一种具有较大潜力的储能技术，正在能源领域崭露头角。液流电池凭借其大容量、高效率以及超长的循环使用寿命等诸多优势，在新能源领域和电力系统中得到了广泛应用和高度认可。这些新兴的储能技术为提高电力系统的稳定性和效率提供了一定的可能性。

2 储能电站的经济性分析

2.1 初期投资成本

首先是储能电站的初期投资成本。储能电站初期投资成本主要包括：一是规划设计成本，这包括进行项目研究和初步设计的费用；二是物资采购成本，涵盖了设备的采购费用以及运输费用；三是工程建设成本，涵盖了设计费、安装调试费、场地费、验收费。上述成本总和即储能电站的初期投资。综合而言，储能电站初期投资成本如下：

cje是储能电站建设所需j类装置单价；Nj是j类装置数目；m是装置种类数；lj是j类装置运输距离；cjt是运输单价；ca是装置的安装调试费；A是储能电站占地面积；cg是单位土地价格。

2.2 运行维护成本

储能设备的操作与维护成本可划分为运营成本和维修成本两部分。其中，运营成本涵盖了由于设备运行所产生的损失费用，以及定期进行的巡检和检查所产生的费用。立足于设备整个生命周期视角出发，为了得出准确的经济评估，需要将通货膨胀、税收等各种经济因素都纳入考量范围，通过综合计算得出一个社会折现率，然后依据这一折现率来确定每年费用的现值。因此，储能电站第t年的运行维护成本通过下述公式来完成计算：

cOM,t是单位容量年运维成本（万元/MW/年）；Psmax是储能电站最大容量。

2.3 储能装置的退役成本

能量存储单元的退役费用主要包括退役处理的人工费用、环境保护费用和销售回收设备的剩余费用。储能设备因其所使用的电池等特殊材质，在退役后将带来较大的环境成本，因此退役后的处理费用在储能设备的总成本中占有相当大的比重。残值是指在资产的使用年限内，在处理一项长期资产时可以预期获得的价值，即资产残值，通过双倍余额递减法来进行精确计算，以确定第a年资产的残值C残值，Ccaptials是资产初期投资金额，资产在折旧年限Nsi到达时的残值为：

储能电站退役成本为：

初始第0年设第1次投运，设第i次投运储能设备寿命周期为Nsi。如达到及，总的投运次数为a+1次。各业务设备寿命不同，投运次数各有差异。再投入费用需计a次，残值则多计一次。若设备未至退役年限，仅计残值，不计人工与环保费。

储能电站成本的现值为：

3 基于粒子群优化算法的储能电站经济性优化方法

3.1 粒子群优化算法

粒子群优化算法是一种高效、收敛速度快的优化方法，具有概念简单、易于实现的特点，需要调节的参数较少[5]。本文采用粒子群优化算法来解决储能电站经济性的优化问题。在电力系统的优化计算和数学模型的求解中，粒子群优化算法得到了广泛地应用。图1展示了粒子群优化算法的计算流程。在粒子群算法中，首先需要初始化种群。然后根据预设的目标函数，计算每个粒子的适应度值。接着随机生成粒子的速度，并保存每个粒子的个体最优值，同时更新粒子群的全局最优值。随后更新粒子的速度与位置，并且扩大种群的规模。在扩大种群规模的每一步中，都会更新每个粒子的个体最优值与粒子群的全局最优值。同时，判断是否达到预设的最大迭代次数或者精度范围。如果满足条件，算法结束。

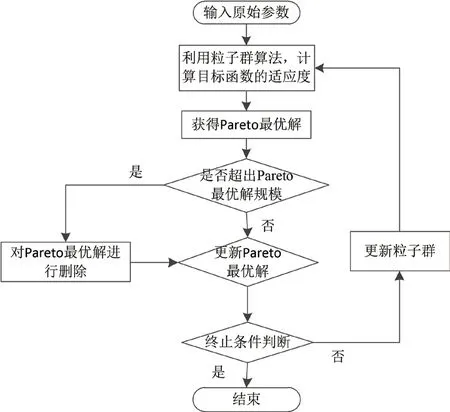
图1 粒子群算法计算流程图

3.2 基于粒子群优化算法的储能电站经济性优化模型

由于储能设备的运行年限一般较长，故也应该从全寿命周期这一长时间尺度去优化储能设备的充放电控制策略，本文详细对此进行了分析。在基于粒子群优化算法的储能电站经济性优化模型当中，本文以储能电站的全寿命周期成本最小为目标函数，如下式所示：

对于基于粒子群优化算法的储能电站经济性优化模型当中的约束条件，包括了储能设备自身的充放电容量约束、充放电次数约束、储能电池的荷电状态约束等。

4 案例分析

近年来，电力用户侧的储能设备安装容量也在不断提高，需要对储能设备的容量配置及运行控制策略进行优化，以便提高储能设备安装的经济性[6]。以某电力用户为例，分析电力储能设备的容量配置及运行控制策略。该电力用户对于供电可靠性的要求较高，该用户的日负荷曲线如图2所示。

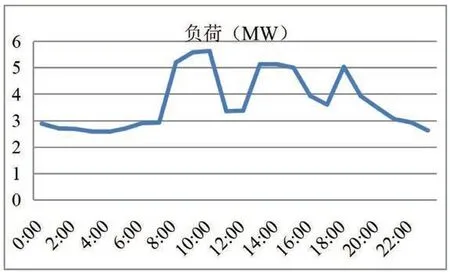
图2 用户的日负荷曲线

假设储能设备的全寿命使用周期为30年，经过对模型采用粒子群算法，并通过MATLAB 软件编程求解，得出了储能设备的最佳安装容量为11.43MWh、储能设备的额定功率为1.42MW，此时储能设备的运行综合效益为110万元。在迭代计算的过程中，迭代次数的收敛曲线如图3所示。

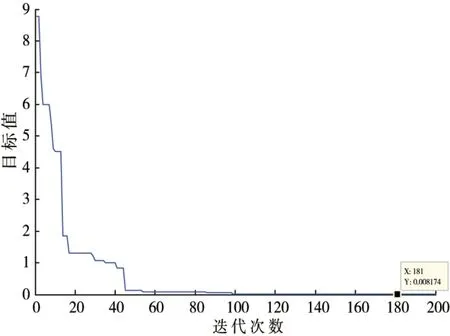
图3 算法的收敛曲线

同时，通过下层优化模型的求解，也得出了储能设备的最佳运行控制策略。储能设备在一天的时间尺度下的充放电运行策略如图4所示。

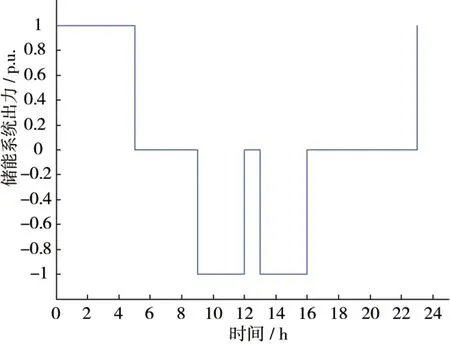
图4 储能设备的运行充放电控制策略

从图4的储能设备运行充放电控制策略中可以看出，在夜间时段，由于此时的负荷较低，故储能设备运行在充电状态，总共充电了一次。而在白天时段，此时的用电负荷水平较高，故储能一般运行在放电状态，以满足用户的实际用电需求，总共放电了两次，达到了优化储能设备运行的目的。本文详细分析了储能设备在运行过程中的成本及效益，并建立了储能设备的运行优化控制模型。采用粒子群算法对所建立的模型进行求解，并开展了算例分析。结果表明，对储能设备的容量及充放电控制策略进行合理地优化，具有较高的经济效益。

综上所述，储能环节的引入为电力系统带来了积极的影响。储能环节的实施能够实现需求侧的有效管理，通过消除昼夜间的电力峰谷差异，实现负荷的均衡分配。提高了电力设备的利用效率，降低了供电成本。同时，储能环节在推动可再生能源利用方面也发挥着重要作用，其能提升系统运行的稳定性，调整电网频率，并对负荷波动进行有效补偿。本文所探讨的基于粒子群优化算法的储能电站经济性优化方法，对于提高电力系统的运行稳定性具有重要意义。