基于广义反演法的不同位置地震引起盆地放大效应的研究

王棪隽 刘启方

摘要：基于强震观测记录，采用广义反演法和HVSR法分析日本仙台盆地48个强震台站以及场地vS30和盆地深度对放大效应的影响。研究表明，相比于广义反演法，HVSR法能够较好地给出场地主频，但会明显低估放大效应的幅值；处于盆地外不同位置的浅源地震引起的盆地放大效应差异明显，仙台盆地南部海域地震引起的放大效应最大，盆地北部陆地地震引起的放大效应最小;盆地南部和东部地震引起的S波的放大效应与vS30的相关性较强，北部地震的放大效应与vS30基本不相关;盆地S波的放大效应与盆地深度在0.5～5 Hz频段内的相关性较强，在0.25～0.5 Hz和5～10 Hz频段内基本不相关。

关键词：仙台盆地; 广义反演; 放大倍数; 盆地深度; S波

中图分类号： TU4      文献标志码：A   文章编号： 1000-0844（2024）03-0614-11

DOI：10.20000/j.1000-0844.20220820002

Basin amplification effect caused by earthquakes at different locations based on the generalized inversion method：a case study of Sendai Basin

WANG Yanjun， LIU Qifang

（Key Laboratory of Structure Engineering of Jiangsu Province， Suzhou Universityof Science and Technology， Suzhou 215009， Jiangsu， China）

Abstract： Based on the strong motion records， the amplification effects of 48 stations in Sendai Basin， Japan， were analyzed by using the generalized inversion and HVSR methods. Then， the impacts of site vS30 and basin depth on the amplification effect were analyzed. Results show that compared with the generalized inversion method， the HVSR method can provide the main frequency of a site， but it underestimates the amplitude of the amplification effect. The amplification effects of the basin induced by shallow earthquakes in different locations outside the basin considerably vary. The amplification effect caused by ocean earthquakes in the southern part of Sendai Basin is the largest， whereas that caused by land earthquakes in the northern part of Sendai Basin is the smallest. The amplification effect of S-wave caused by earthquakes in the southern and eastern parts of the basin shows a strong correlation with vS30， whereas that in the northern part shows little correlation with vS30. The amplification effect of the S-wave in the basin is strongly correlated with the depth of the basin in the frequency band of 0.5-5 Hz but is basically irrelevant in the frequency band of 0.25-0.5 and 5-10 Hz.

Keywords：Sendai Basin; generalized inversion method; amplification factor; basin depth; S-wave

0 引言

影響盆地放大效应的因素，除了众所周知的震源（震级、震源深度和断层类型等）、距离（几何扩散和非弹性衰减）和场地（vS30和覆盖层厚度）三个因素外，还包括台站相对于盆地的位置、震源相对于盆地的位置和震源到达盆地的入射角等因素。

广义反演法（GIT）由Andrews［1］首先提出，可以分离傅里叶振幅谱中依赖频率传播的路径效应、场地效应和震源效应。一些学者已通过这种方法来处理全球范围内的地震动数据［2-7］。

由于不同位置震源到达盆地的入射角和路径不同，所以不同震源引起的盆地地震动放大也不同。已有的研究表明，沉积盆地中存在复杂的路径衰减和强烈的场地效应［8-13］。强烈地震动很可能是由于盆地产生的面波对体波存在较强的影响，这些影响在盆地边缘局部存在，已被证实是地震损害增强的主要原因，如1995年神户地震发生的神户损害带［11］，以及1994年北岭地震圣莫尼卡地区的特别损害带［8］。盆地的不规则形状导致地震传播的路径不同，从而产生的聚焦效应也不同，因此分析不同位置震源作用下盆地的放大差异有重要价值。

本文将广义反演法应用于仙台盆地105次地震的3 327组记录的大量地震数据集，以分离震源、场地和路径效应;将衰减函数进行参数化，得到了与频率相关的S波品质因子;利用ω-2模型对分离的震源谱进行解释［14-15］;比较并分析了利用GIT反演的场地放大倍数与利用HVSR法计算的场地放大倍数之间的关系；重点分析了不同位置震源引起的场地放大倍数与vS30和盆地深度的关系。

1 分析方法

1.1 参数化广义反演法

参数化广义反演法可以分离观测到的傅里叶振幅谱中依赖频率的传播路径效应、场地效应和震源效应三项因素。观测记录的地震动傅里叶振幅谱在频域中可以表示为以下三项的乘积：

Oij（f，Mi，Rij）=Si（f，Mi）·Pij（f，Rij）·Gj（f）（1）

式中：Oij（f，Mi，Rij）是i震源在j台站观测到的震级为Mi，频率为f的S波傅里叶振幅谱，Rij为i震源到j台站的震源距;Si（f，Mi）表示i震源在频率为f时的震源谱;Pij（f，Rij）为i震源到j台站的路径衰减;Gj（f）为j台站的场地放大效应。对式（1）的两边取对数，可将式（1）线性化为式（2）：

lnOij（f，Mi，Rij）=lnSi（f，Mi）+lnPij（f，Rij）+lnGj（f）（2）

1.2 单步非参数化广义反演法

Oth等［5］在研究日本地震动特性时提出了单步非参数化广义谱反演方法，以便更稳定地分离日本地震动的传播路径效应、场地效应和震源效应三项因素。式（2）可以表示为Ax=b的线性方程组，其中b为所有台站记录到的S波的傅里叶振幅谱的一维向量;x为震源谱、场地放大倍数、路径衰减这些未知项的一维向量;A为表示两者关系的稀疏矩阵。矩阵形式如下：

100·…-100·…-100·…

010·…-100·…-100·…

····…-····…-····…

100·…-010·…-010·…

w100·…-000·…-····…

000·…-w300·…-····…

-w22w2-w22·…-000·…-····…

0-w22w2-w22…-····…-····…

····…-····…-····…×

lnP（f，RBin1）

lnP（f，RBinND）…

lnG1（f）

lnGNS（f）…

lnS1（f，M1）

lnSNE（f，MNE）=lnO1（f，M1，R1）lnOij（f，Mi，Rij）00（3）

式（3）中，路徑衰减项（P）、场地放大项（G）、震源项（S）垂直叠加，并以水平虚线分隔;在稀疏矩阵中，由两条垂直虚线分隔的左、中、右子矩阵，分别与路径衰减项（P）、场地放大项（G）、震源项（S）相对应;w1是路径衰减的权重系数，使lnP（f，RBin1）=0，其中RBin1为最小震源距;权重系数w2用来约束路径衰减曲线，使其变得平滑，尽可能排除场地相关的影响因素;权重系数w3是一个限制条件，用来消除场地放大系数和震源项之间存在的权衡，对应参考场地的场地放大系数。

2 数据筛选及数据处理

2.1 地震动记录筛选

本研究中使用的数据均来自日本K-NET和KiK-net（井上），通过下列原则从仙台盆地周边筛选数据：（1）震级MJMA>4;（2）震源距在5～250 km;（3）震源深度不大于30 km;（4）每个台站至少有4次地震记录，每次地震至少被4个台站记录。最终数据库包含了105次地震，48个台站的3 327组记录。图1是地震动记录的震级和震源距的关系。

为了研究地震震源位置对盆地S波放大效应的影响，我们依据震源相对盆地的空间分布将地震记录划分为3个研究区域，如图2所示。区域Ⅰ包含48个台站在27次M4.0～5.9地震中记录到的1 101组数据，用红色圆形表示;区域Ⅱ包含47个台站在10次M4.0～5.8地震中记录到的214组数据，用黄色圆形表示;区域Ⅲ包含48个台站在68次M4.0～6.4地震中记录到的2 012组数据，用蓝色圆形表示。本文以地下剪切波速为vS=1.5 km/s的等值面为盆地底部［16］，定义为Z1.5，深度等值线如图2（b）所示，其中标记为黄色的上三角形为位于盆地外的参考基岩台，黑色的上三角形为选取的所有台站。

2.2 地震动记录的数据处理

（1） 对原始记录进行零线校准，再以0.2～30 Hz为滤波频带进行滤波，以减少噪声对记录的影响。

（2） 采用Husid Plot函数［17］识别S波的起始时间，计算如下：

Hn（T）=∫T0［a（t）］2dt∫∞0［a（t）］2dt （4）

式中：Hn（T）为Husid Plot函数，反映了整个加速度时程能量分布;a（t）为加速度时程，以函数值急剧增加的点为S波的起始时间。

S波的结束时间，采用累积均方根函数（CRMS）来识别［18］，计算如下：

CRMS（T）=1T∫T0‖a（t）‖2dt （5）

式中：CRMS（T）为累积均方根函数;a（t）为加速度时程，以函数值开始下降的点为S波的结束时间。

为了保证记录对频率的分辨率要求，提取到的S波记录长度至少是4 s，使傅里叶谱的分辨率达到0.25 Hz，同时为了避免面波对S波的干扰，提取到的S波记录至多是12 s。在确定S波的起止时间后，在S波前后各多截取10%的S波长度数据，并且乘以边瓣余弦函数窗，来减少截断误差。图3给出了基于上述方法截取的一条S波地震动记录。

（3） 直接通过傅里叶变化得到的曲线有很多毛刺，在进行反演时这些尖刺峰值可能会影响反演结果，因此采用0.5 Hz的矩形窗对S波记录进行平滑处理。

2.3 参考台站的选取

为了消除震源项和场地放大项之间存在的影响，必须将一个合适的台站作为参考场地，将这个台站的放大倍数在所有频率范围内设置为2。一般按照下列条件选取作为参考场地的基岩台站：（1）vS30>600 m/s的场地钻孔剪切波速;（2）H/V谱比曲线较为平坦且幅值较小。

本研究选取台站MYGH03为参考台站，在计算范围内将这个台站的场地放大系数假设为2，即GMYGH03（f）=2。该台站覆盖层30 m处的平均剪切波速vS30=934 m/s，可近似认为是岩石场地;同时该台站的H/V谱比曲线较为平坦且幅值较小，满足参考台站的选取要求（图4）。

3 结果分析和讨论

3.1 震源谱及震源参数的计算

图5给出了通过广义反演计算得到的105次地震的位移震源谱。本文计算了这些地震的地震矩密度函数M0i（f）˙，计算如下［19］：

Si（f）=（2πf）2·RθφVF4πρV3sR0·M0i（f）˙（6）

式中：Rθφ为辐射花样系数，通常取平均值0.63［20］;V表示横波能量分為两个水平分量，取12;ρ为地壳介质的密度，本文取2.7 g/cm3;vS为地壳介质平均剪切波速，本文取3.6 km/s;R0为参考距离，通常取1 km;M0i（f）表示第i次地震在频率f处的地震矩，可按下式计算：

M0i（f）˙=M0i1+ffc2 （7）

式中：M0i为第i次地震的地震矩；fc为拐角频率。采用Andrews［1］提出的利用震源谱估计拐角频率fc和震源谱平台值Ω0的方法，定义了两个积分常数SD2和SV2，由以下公式计算得出：

SD2=2∫∞0D2（f）df （8）

SV2=2∫∞0V2（f）df （9）

式中：D（f）为位移谱，可由加速度谱D（f）=A（f）（2πf）2得出;V（f）为速度谱，可由加速度谱V（f）=A（f）2πf得出。

假设震源谱符合Brune的ω-2震源模型，那么D（f）可表示为：

D（f）=Ω01+ffc2 （10）

联立式（8）～（10），可得：

fc=12πSD2SV2 （11）

Ω0=2SD2πfc （12）

同时，可得地震矩M0：

M0=4πρV3sΩ0Rθφ （13）

采用该方法计算了各地震的M0和fc，以最小二乘法拟合数据，结果如图6所示。

lg（M0）=24.74-2.26lg（fc） （14）

lg（M0）=22.77-2.37lg（fc） （15）

通过与任叶飞［21］得出的结果［式（15）］进行比较，发现两者的各项系数比较接近，说明本文得到的震源谱较为可靠。

3.2 反演的品质因子分析

反演的过程中计算了与距离有关的路径衰减函数Pij（f，Rij）。从6～210 km的距离被分成102个2 km宽的分段;在R=6 km处，Pij（f，Rij）在所有频率范围设定为1;衰减函数Pij（f，Rij）包含着由几何扩散引起的衰减和由Q值引起的衰减，Q值可以通过假设几何扩散模型通过计算得到。 本文假设几何传播的函数为：

G（R）=R0Rα （16）

式中：R为震源距;R0为参考距离，由于观测记录中的最小震源距为6 km，因此将参考距离R0取为6 km;α为衰减指数，是S波的几何扩散。利用品质因子Q和几何扩展G（R）可以估计路径衰减函数。频率相关的路径衰减函数Pij（f，Rij）可以通过下式计算：

lnPij（f，Rij）-lnG（Rij）=-πfRijQ（f）Vs（17）

式中：Rij为第i次地震到第j个台站的震源距;Q（f）为品质因子;vS为S波平均剪切波速，取3.6 km/s。

Q（f）作为表征地震动衰减特性的函数，通常表示为指数形式Q（f）=Q0fα（Q0、α为常数）。通过对衰减函数所得结果采用最小二乘法回归拟合，得到区域Ⅰ、Ⅱ、Ⅲ地区经验关系分别为117f1.0、75.2f0.7、120.2f1.1。如图7所示，图中蓝色直线和散点表示区域Ⅰ的品质因子，红色直线和散点表示区域Ⅱ的品质因子，黑色直线和散点表示区域Ⅲ的品质因子。图7中还给出了Oth等［5］基于日本东部地区地震反演得到的Q（f）结果（黑色虚线）。图7中可以看出，本文反演得到的区域Ⅰ、Ⅲ地区的Q（f）要略大于Oth等［5］计算结果，区域Ⅱ地区的Q（f）要略小于Oth等［5］计算结果。考虑到Oth等［5］选取的是整个日本火山带东侧的数据，也就是区域Ⅱ所在位置，这就意味着区域Ⅰ、Ⅲ地区S波非弹性衰减要快于东部地区。另外，本文选取的是震源距范围6～210 km的强震动记录，而Oth［5］选取的数据震源距均小于150 km。

3.3 反演的场地放大效应分析

3.3.1 HVSR法和GIT法得到的场地反应比较

在0.1～20 Hz的频率范围内，以48个台站中位于盆地中心的15个台站的场地放大系数Gj（f）为例与HVSR法比较，如图8所示。其中实线为各台站广义反演估算的站点放大系数，蓝色表示区域Ⅰ，红色表示区域Ⅱ，黑色表示区域Ⅲ;图中虚线为各区域通过HVSR法计算的结果。HVSR法假设局部场地条件对地面运动的垂直分量没有显著影响，HVSR法可以用作场地放大的指标。以往的研究表明［21］，HVSR法与场地的地质条件一致，能够揭示主要的频率峰值。然而，通常的结论是，该方法在振幅水平上有衰减，特别是对高阶频率，且水平和垂直分量都受到散射和吸收造成的能量损失的影响。因此，HVSR除了场地的放大效应外，也反映了高频能量的一些衰减。

从图8中可以看出，对于部分台站（如IWTH26、MYG003、MYGH08），GIT法和HVSR法获得的场地反应较一致;但对于大部分台站，GIT得到的场地反应都要大于HVSR得到的结果，如图9所示。两种方法得到场地反应差异的主要原因是：Parolai［22］通过数值模拟及分离不同震源对HVSR的影响，发现在波阻抗变化大的基岩-土层交界面，S波和P波转换引起垂直方向的场地放大，从而导致HVSR估计的场地反应偏小。对于不同地理位置的震源，部分台站如IWTH26、MYG012、MYG013、MYG014及MYGH08三个区域所得到的场地放大均较为相似;其余大部分台站三个区域通过GIT法所得到的场地放大均有较大差异，对于大部分台站，区域Ⅲ产生的场地反应最大，区域Ⅰ其次，区域Ⅱ产生的场地反应最小;而HVSR法得到的结果并不能看出明显的差异。

3.3.2 场地放大系数与场地地质条件的关系

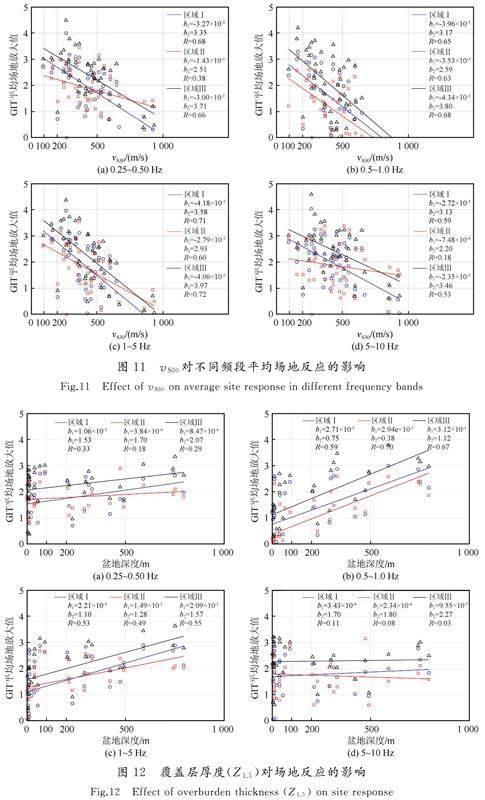
地表土层30 m处的剪切波平均速度（vS30）是用于衡量强运动振幅和土壤或岩石分类的重要现场参数。对于有钻孔资料的台站，本文根据已有的数据如图10 ，通过延拓法（Wang等［23］）计算这些台站的vS30。在对数刻度下分别对三个区域在0.25～0.5 Hz、0.5～1 Hz、1～5 Hz和5～10 Hz的平均场地放大因子通过最小二乘法拟合线性关系，拟合结果如图11所示。拟合公式为：

ln（y）=b1·vS30+b2 （18）

式中：y为放大倍数；vS30为地表土层30 m处的剪切波平均速度。

结果显示，区域Ⅰ和Ⅲ在4个频段内的平均场地放大与vS30都存在较强的相关性，其中，0.5～1 Hz和1～5 Hz内的相关性会更强，斜率分别为-3.96×10-3、-4.34×10-3、-4.18×10-3、-4.06×10-3，相关系数也都达到了0.65以上;区域Ⅱ仅在0.5～1 Hz和1～5 Hz内存在较强的相关性，直线斜率为-3.53×10-3和-2.79×10-3，相关系数分别为0.63和0.60，而0.25～0.5 Hz和5～10 Hz内基本不相关，在这两个频段内的相关系数都小于0.5。

3.3.3 场地放大系数与盆地深度的关系

盆地的场地放大与震源的位置息息相关，不同位置震源入射到盆地的角度和盆地形状的不同，导致盆地的放大效应也不同［24-27］。为了分析不同地震位置S波放大与盆地深度的关系，本文以地下剪切波速vS=1.5 km/s的等值面为盆地底部，定义为Z1.5，在对数刻度下拟合了Z1.5与不同频率段内三个区域平均场地放大因子的线性关系，如图12所示，拟合公式为：

ln（y）=b1·h+b2 （19）

式中：y为放大倍数;h为盆地深度。

图12中，每个散点代表一个台站所在位置的盆地深度和GIT反演的平均场地放大倍数，直线表示相应区域拟合的线性关系，蓝色表示区域Ⅰ，红色表示区域Ⅱ，黑色表示区域Ⅲ。

从总体上看，区域Ⅲ在各频段内的放大倍数（斜率均值为1.75×10-3）均大于区域Ⅰ（1.58×10-3）、Ⅱ（1.262×10-3）的斜率均值;而区域Ⅰ在0.25～0.5 Hz和1～10 Hz频段内盆地深度小于200 m时放大倍数略小于区域Ⅱ，之后随着盆地深度的增加逐渐大于区域Ⅱ。

从图12中可以看出，在0.25～5 Hz频率段三个区域的放大倍数与盆地深度的相关性均较弱，斜率均值为0.764×10-3;在0.5～1 Hz频率段，随着盆地深度的增加，放大倍数明显上升，放大倍數与盆地深度有较强的相关性，斜率均值为2.92×10-3是0.25～5 Hz时的约4倍。当频率处于1～5 Hz时，放大倍数与盆地深度依然有较强的相关性，斜率均值为1.93×10-3是0.25～5 Hz时的2.5倍左右。但是，当频率超过5 Hz时放大倍数与盆地深度的相关性开始减弱，在5～10 Hz时，放大倍数与盆地深度基本不相关，甚至出现轻微的负相关，即放大倍数随着盆地深度增加逐渐变小。

4 结论

本文利用日本K-NET和KiK-net记录的大量地震动数据，选取了仙台盆地周边48个台站在105次地震中观测的3 327组记录，通过广义反演法（GIT）分析了地震波的震源谱、路径衰减和台站的场地放大效应。通过对震源谱的研究，得出了拐角频率与地震矩的函数关系，并通过与其他研究的结果比较，证明了震源谱的可靠性。拟合所得的品质因子表明仙台盆地南部和东部震源S波衰减较快且与频率存在很强的相关性，北部震源S波衰减较慢。在对得到的场地效应进行重点分析后，获得了如下结论：

（1） 将本文得到的场地放大效应数据与HVSR法的结果进行了比较，发现HVSR法与广义反演技术得到的函数形状吻合良好。可以看出，两种方法得到台站放大倍数的形状基本上是相同的，但大部分站点HVSR法的反应幅值明显低于广义反演的结果。说明HVSR法能很好地估计场地放大的峰值频率，但是会低估场地反应幅值。

（2） 通过对不同震源位置GIT法获得场地放大效应的分析，发现盆地对不同震源位置地震波的放大不同。因此，我们在对数刻度下分别回归分析三个区域在0.25～0.5 Hz、0.5～1 Hz、1～5 Hz和5～10 Hz频段内平均场地放大倍数与盆地深度的线性关系，发现盆地南部海域地震的场地放大效应明显大于盆地北部和东部，而盆地东部地震场地反应略大于盆地北部。另外，我们发现在0.5～5 Hz频段，放大倍数随着盆地深度逐渐增大，但是在0.25～0.5 Hz和5～10 Hz频段内两者的相关性变得很弱。盆地东部和南部地震所引起的场地反应与盆地深度的相关性较好，覆盖层越厚，盆地引起的场地反应越大。

（3） 本文进一步分析了不同位置震源对同一台站引起的场地放大效应与vS30的关系，发现三个区域在0.5～1 Hz和1～5 Hz频段内的平均场地放大倍数与vS30的相关性较强;在0.25～0.5 Hz和5～10 Hz频段内的相关性较弱。其盆地北部地震所引起的场地放大效应在0.25～0.5 Hz和5～10 Hz频段内无明显相关性。

本文僅考虑了不同位置震源对盆地放大效应的影响，进一步工作可考虑不同深度震源对盆地放大效应的影响。

参考文献（References）

［1］ ANDREWS D J.Objective determination of source parameters and similarity of earthquakes of different size［M］//Earthquake Source Mechanics.Washington D.C.：American Geophysical Union，2013：259-267.

［2］ CASTRO R R，ANDERSON J G，SINGH S K.Site response，attenuation and source spectra of S waves along the Guerrero，Mexico，subduction zone［J］.Bulletin of the Seismological Society of America，1990，80：1481-1503.

［3］ CASTRO R R，PACOR F，SALA A，et al.S wave attenuation and site effects in the region of Friuli，Italy［J］.Journal of Geophysical Research：Solid Earth，1996，101（B10）：22355-22369.

［4］ OTH A，PAROLAI S，BINDI D，et al.Source spectra and site response from S waves of intermediate-depth Vrancea，Romania，earthquakes［J］.Bulletin of the Seismological Society of America，2009，99（1）：235-254.

［5］ OTH A，BINDI D，PAROLAI S，et al.Spectral analysis of K-NET and KiK-net data in Japan，part II：on attenuation characteristics，source spectra，and site response of borehole and surface stations［J］.Bulletin of the Seismological Society of America，2011，101（2）：667-687.

［6］ OTH A.On the characteristics of earthquake stress release variations in Japan［J］.Earth and Planetary Science Letters，2013，377-378：132-141.

［7］ WANG H W，REN Y F，WEN R Z.Source parameters，path attenuation and site effects from strong-motion recordings of the Wenchuan aftershocks （2008—2013） using a non-parametric generalized inversion technique［J］.Geophysical Journal International，2018，212（2）：872-890.

［8］ GRAVES R W.Modeling three-dimensional site response effects in the Marina District Basin，San Francisco，California［J］.Bulletin of the Seismological Society of America，1993，83（4）：1042-1063.

［9］ HANKS T C.Strong ground motion of the San Fernando，California，earthquake：ground displacements［J］.Bulletin of the Seismological Society of America，1975，65（1）：193-225.

［10］ LIU H L，HEATON T.Array analysis of the ground velocities and accelerations from the 1971 San Fernando，California，earthquake［J］.Bulletin of the Seismological Society of America，1984，74（5）：1951-1968.

［11］ KAWASE H.The cause of the damage belt in Kobe：“the basin-edge effect” constructive interference of the direct S-wave with the basin-induced diffracted/rayleigh waves［J］.Seismological Research Letters，1996，67（5）：25-34.

［12］ PITARKA A，IRIKURA K，IWATA T，et al.Three-dimensional simulation of the near-fault ground motion for the 1995 Hyogo-Ken Nanbu （Kobe），Japan，earthquake［J］.Bulletin of the Seismological Society of America，1998，88（2）：428-440.

［13］ SCHNABEL P B.SHAKE-a computer program for earthquake response analysis of horizontally layered sites［J］.Eerc，1972，70（18）：41278.

［14］ BRUNE J N.Tectonic stress and the spectra of seismic shear waves from earthquakes［J］.Journal of Geophysical Research，1970，75（26）：4997-5009.

［15］ BRUNE J N .Journal of geophysical research［J］.American Geophysical Union，1971，36（3）：1766-1181.

［16］ 李春果.基于強震动记录残差分析的关东盆地放大效应研究［D］.哈尔滨：中国地震局工程力学研究所，2019.

LI Chunguo.Research of kanto basin amplification effect based on residual analysis of ground-motion recordings［D］.Harbin：Institute of Engineering Mechanics，China Earthquake Administration，2019.

［17］ RA L.Gravity effects on the earthquake response of yielding  structures［J］.California Institute of Technology，1967，71（16）：31589.

［18］ MCCANN M，SHAH H.Determining strong-motion duration of earthquakes［J］.Bulletin of the Seismological Society of America，1979，69（4）：1816-1825.

［19］ KANAMORI H.Mechanism of tsunami earthquakes［J］.Physics of the Earth and Planetary Interiors，1972，6（5）：346-359.

［20］ 裴顺平，许忠淮，汪素云.中国大陆及邻近地区上地幔顶部Sn波速度层析成像［J］.地球物理学报，2004，47（2）：250-256.

PEI Shunping，XU Zhonghuai，WANG Suyun.Sn wave tomography in the uppermost mantle beneath the China continent and adjacent regions［J］.Chinese Journal of Geophysics，2004，47（2）：250-256.

［21］ 任叶飞.基于强震动记录的汶川地震场地效应研究［D］.哈尔滨：中国地震局工程力学研究所，2014.

REN Yefei.Study on site effect in the Wenchuan earthquake using strong-motion recordings［D］.Harbin：Institute of Engineering Mechanics，China Earthquake Administration，2014.

［22］ PAROLAI S.Comparison of different site response estimation techniques using aftershocks of the 1999 Izmit earthquake［J］.Bulletin of the Seismological Society of America，2004，94（3）：1096-1108.

［23］ WANG H Y，WANG S Y.A new method for estimating vS（30） from a shallow shear-wave velocity profile （depth 30 m）［J］.Bulletin of the Seismological Society of America，2015，105（3）：1359-1370.

［24］ DAVIS P M，RUBINSTEIN J L，LIU K H，et al.Northridge earthquake damage caused by geologic focusing of seismic waves［J］.Science，2000，289（5485）：1746-1750.

［25］ CHOI Y.Empirical model for basin effects accounts for basin depth and source location［J］.Bulletin of the Seismological Society of America，2005，95（4）：1412-1427.

［26］ IWAKI A，IWATA T.Simulation of long-period ground motion in the Osaka sedimentary basin：performance estimation and the basin structure effects［J］.Geophysical Journal International，2010，181（2）：1062-1076.

［27］ 刘启方，刘晓光.基于强震记录的大阪盆地S波和次生波放大效应研究［J］.自然灾害学报，2021，30（6）：32-42.

LIU Qifang，LIU Xiaoguang.Study on the amplification effect of S wave and basin induced wave of Osaka Basin based on strong motion records［J］.Journal of Natural Disasters，2021，30（6）：32-42.

（本文编辑：任 栋）

基金项目：国家自然科学基金项目（51978434）

第一作者简介：王棪隽（1997-），男，硕士研究生，主要从事盆地放大研究。 E-mail：542966504@qq.com。

通信作者：刘启方（1969-），男，研究员，博士，主要从事地震工程研究。E-mail：qifang_liu@126.com。

王棪隽，刘启方.基于广义反演法的不同位置地震引起盆地放大效应的研究——以仙台盆地为例［J］.地震工程学报，2024，46（3）：614-624.DOI：10.20000/j.1000-0844.20220820002

WANG Yanjun，LIU Qifang.Basin amplification effect caused by earthquakes at different locations based on the generalized inversion method： a case study of Sendai Basin［J］.China Earthquake Engineering Journal，2024，46（3）：614-624.DOI：10.20000/j.1000-0844.20220820002