基于高斯过程模型的桥梁时变系统地震易损性分析

万华平 彭紫鑫 卫志成 陈昊 苏雷

摘要：桥梁在长期服役过程中面临的氯离子侵蚀作用会导致材料性能退化，进而影响桥梁结构的抗震性能。准确评估服役桥梁的抗震性能可以有效保障和提高桥梁结构的安全性，因此开展考虑时变效应的桥梁地震易损性分析非常必要。考虑到地震易损性分析涉及大量的动力时程分析，计算效率很低，故采用高斯过程模型取代耗时的动力时程分析，旨在提高地震易损性分析效率。以一座三跨连续梁桥为例，探究氯离子侵蚀作用下桥墩材料性能的退化规律，建立纵筋、箍筋以及保护层和核心混凝土材料性能退化时变曲线;基于高斯过程模型和联合概率地震需求模型，建立桥梁系统在不同服役年限下的易损性曲线和曲面。结果表明：（1）氯离子侵蚀作用明显降低了桥墩钢筋混凝土材料的强度；（2）氯离子侵蚀作用明显提高了高等级损伤的桥梁地震易损性，結构更容易发生高等级损伤。

关键词：氯离子侵蚀; 桥梁结构; 地震易损性; 时变效应; 高斯过程模型

中图分类号： U442.5+5      文献标志码：A   文章编号： 1000-0844（2024）03-0511-10

DOI：10.20000/j.1000-0844.20220824004

Seismic fragility analysis of the time-varying system

of a bridge with a Gaussian process model

WAN Huaping1， PENG Zixin1， WEI Zhicheng2， CHEN Hao1， SU Lei3

（1. College of Civil Engineering and Architecture， Zhejiang University， Hangzhou 310058， Zhejiang， China;

2. Hefei Cement Research and Design Institute Co.， Ltd.， Hefei 230051， Anhui， China;

3. School of Civil Engineering， Qingdao University of Technology， Qingdao 266520，Shandong， China）

Abstract：  Chloride ion erosion in bridges in long-term service leads to the degradation of material properties and affects the seismic performance of bridge structures. Accurately evaluating the seismic performance of bridges in service can effectively guarantee and improve the safety of bridge structures. Therefore， seismic fragility analysis considering a time-varying effect is essential. In this study， the time-varying seismic fragility analysis of bridges was carried out. The degradation of material properties caused by chloride ion erosion on the seismic performance of the bridge was considered. Given that seismic fragility analysis involves comprehensive dynamic time-history analysis， the calculation efficiency is low. Thus， the Gaussian process model was used to replace the time-consuming dynamic time-history analysis to improve the efficiency of the analysis. The degradation law of the pier material properties under the action of chloride ion erosion was explored in a three-span continuous beam bridge. Then， the degradation time-varying curves of the longitudinal reinforcement， stirrup， protective layer concrete， and core concrete were established. Based on the Gaussian process and probabilistic seismic demand models， the fragility curves and surfaces of bridge systems with different service years were established. Results show that （1） the strength of the reinforced concrete materials of piers is substantially reduced by chloride ion erosion， and （2） chloride ion erosion obviously increases the seismic fragility of the bridge with high-level damage， and the structure is more prone to high-level damage.

Keywords：chloride ion erosion; bridge structure; seismic fragility; time-varying effect; Gaussian process model

0 引言

地震灾害会对桥梁结构造成巨大损伤，桥梁结构抗震性能准确评估对于桥梁结构服役安全保障具有重要意义。除了地震作用以外，桥梁在服役过程中还受到复杂环境因素的影响，其中氯离子侵蚀是重要影响因素。氯离子侵蚀主要引起桥梁组成材料的性能退化，同时对钢筋与混凝土之间的相互黏结以及箍筋对核心混凝土的约束造成一定影响，这些影响最终均会引起桥梁钢筋混凝土构件的强度下降，进而影响地震作用下桥梁整体结构安全性。因此，处于近、跨江河和海的桥梁结构以及长期接触含氯盐土壤的桥梁结构，在进行地震易损性分析时，应考虑氯离子侵蚀引起的时变效应。

国内外学者已对受侵蚀因素影响下的桥梁材料性能和抗震性能进行了一系列研究。Stewart［1］建立了点蚀作用下钢筋混凝土梁弯曲和剪切极限状态的时变空间可靠度模型。Kumar等［2］分析了桥梁累积地震和氯离子侵蚀的共同影响，建立了时变易损性曲线。李磊等［3］研究了纵筋锈蚀率引起的锈蚀钢筋混凝土柱刚度、承载力、耗能和变形的影响，建立了锈蚀钢筋混凝土柱抗震性能指标的衰变模型。赵珺等［4］研究了氯离子侵蚀对某三跨预应力连续刚构桥抗震性能的影响，得到桥梁构件及整体的易损性曲线及地震风险曲线。以上研究主要集中在侵蚀环境对桥梁构件材料性能的影响，在桥梁系统抗震性能分析方面的研究工作较少。

桥梁系统地震易损性通过整个桥梁结构的损伤来全面评估桥梁的抗震性能。Nielson［5］采用联合概率地震需求模型方法建立了桥梁系统易损性曲线。地震易损性分针析涉及大量的非线性动力时程分析，计算非常耗时。因此，本文采用高斯过程模型进行简化计算，有效降低动力时程分析计算时间，提高计算效率。高斯过程模型是一种基于贝叶斯理论的机器学习方法，能很好地解决高维度、小样本和强非线性等复杂问题，在工程领域已经得到广泛应用［6-7］。

本文阐述了氯离子在桥梁材料中的扩散和侵蚀机理，研究了在氯离子侵蚀作用下桥墩钢筋和混凝土材料的强度性能退化规律，建立了不同服役时期的桥梁结构有限元模型;考虑了桥墩损伤指标和桥梁各构件间的相互影响，建立了桥梁各构件的地震需求模型和能力模型;以构件地震易损性为基础并结合各构件相关系数矩阵，进行系统地震易损性分析;利用高斯过程模型进行简化分析计算，得到了不同服役时间的桥梁系统地震易损性曲线和曲面。

1 侵蚀作用下的材料性能退化

1.1 氯离子扩散机理

氯离子侵蚀以钢筋开始锈蚀时间为界包含两个过程，即锈蚀开始前的氯离子渗透扩散阶段和锈蚀开始后的材料性能退化阶段。Fick第二定律可以描述氯离子在混凝土材料中的扩散过程，距离混凝土材料表面不同深度处的氯离子浓度随时间变化的表达式为［8］：

C（x，t）=CS1-erfx2Dct

Dc=DrefF1（T）F2（t）F3（h） （1）

式中：C（x，t）为氯离子浓度;x为距混凝土表面的深度;Cs为混凝土表面氯离子浓度;erf（·）为误差函数;Dc为扩散系数;Dref为考虑温度及湿度影响的经验扩散系数;F1（T）为环境温度系数;F2（t）为混凝土材料龄期系数;F3（h）为环境相对湿度系数。其中，各项系数的计算表达式为［8］：

lgDref=a+blgwc

F1（T）=expUR1Tref-1T

F2（t）=treftm

F3（h）=1+（1-h）4（1-hc）4-1 （2）

式中：a、b均为经验系数，a取-10.6，b取1.9;w/c为水灰比;U为氯离子扩散过程中的活化能，当w/c为0.4、0.5和0.6时，U分别为41.8、44.6和32.0 kJ/mol;R为气体常数，取8.314 J/mol·K;Tref为参考温度，取296 K;tref为参考时间，取28天;m为龄期经验参数，取0.04;h为相对湿度;hc为临界湿度，取75%。

1.2 材料性能退化

在氯离子侵蚀作用下，材料性能退化主要表现在钢筋和混凝土性能的退化。钢筋的主要锈蚀方式是点蚀，点蚀随机发生在钢筋的长度范围内，并引起钢筋表面缺陷，形成深坑。为表示点蚀对钢筋的性能退化的影响规律，可将点蚀形成的深坑近似按四边形处理。由此，可得钢筋点蚀面积Acor的计算公式为［9］：

Acor（t）=

A1+A2，P（t）≤d2

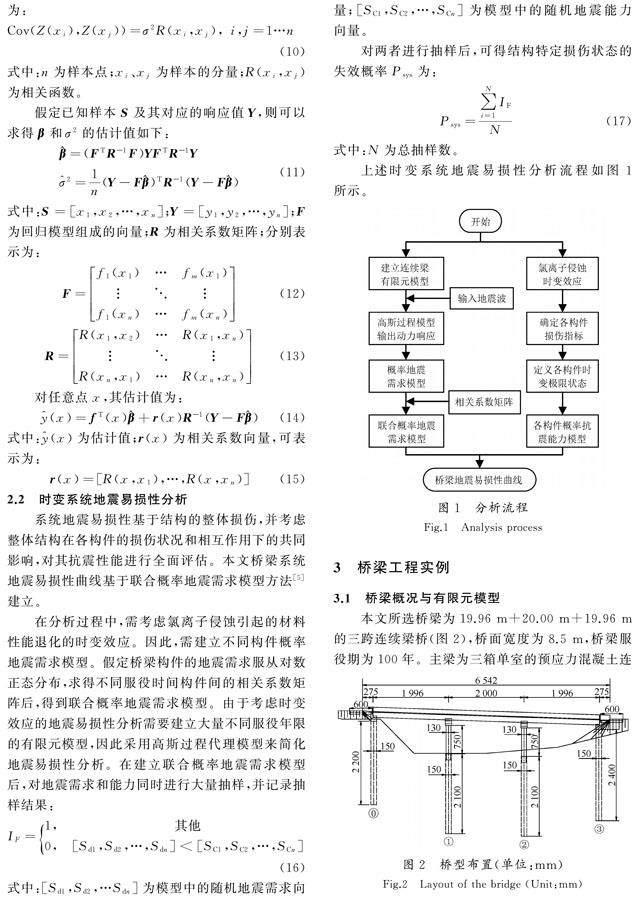
πd24-A1+A2，d2

πd24，P（t）>d（3）

式（3）中各参数可按下式计算［9］：

A1=12θ1d22-b2d2-b2

A2=12θ2P（t）2-bP（t）2d

θ1=2arcsinbd，

θ2=2arcsinb2P（t）

b=2P（t）1-P（t）d2，

P（t）=0.011 6icorRt

icor（t）=0.85icor（1）t-0.29

icor（1）=3.781-wc-1.64z（4）

式中：A1、A2为点蚀模型的面积参数;θ1、θ2为四边形对角角度;b为四边形对角线长度;d为钢筋初始直径;P（t）为点蚀深度;icor为侵蚀速率;icor（1）为初始侵蚀速率;R为点蚀系数;t为服役时间减去腐蚀开始时间;z为保护層混凝土厚度。

钢筋锈蚀面积的增加会导致钢筋的材料性能降低，主要表现为钢筋强度的变化。氯离子侵蚀作用下钢筋屈服强度和极限强度与钢筋锈蚀面积间的定量关系可表示为［10］：

fy=（1-βyQcor）fy0

fu=（1-βuQcor）fu0 （5）

式中：fy0和fy分别为钢筋锈蚀前、后的屈服强度;fu0和fu分别为钢筋锈蚀前、后的极限强度;βy、βu均为强度折减系数，βy取0.005，βu取0.006 5;Qcor为钢筋锈蚀率，可表示为［10］：

Qcor=AcorA0 （6）

式中：A0表示钢筋未锈蚀时的初始面积；Acor表示钢筋未锈蚀后的面积。

此外，在氯离子侵蚀作用下，会对保护层混凝土以及核心混凝土的材料性能造成退化，主要表现为抗压强度的变化。开裂后保护层混凝土的抗压强度可按下式计算［11］：

fcor=fc1+Kε1ε0 （7）

式中：fc和fcor分别为保护层混凝土在侵蚀前、后的抗压强度;K为与钢筋性质相关的系数;ε0为未开裂混凝土峰值应变;ε1为横向平均拉应变，可按下式计算［11］：

ε1=nbarswcrb0

wcr=2π（vrs-1）X （8）

式中：nbars为受拉钢筋数量;b0为构件开裂前截面宽度;wcr为总裂缝宽度;vrs为钢筋锈蚀膨胀系数，取为2;X为锈蚀深度。

2 基于高斯过程模型的桥梁时变系统地震易损性分析

2.1 高斯过程模型

回归模型和随机过程共同组成了高斯过程模型，其表达式为：

y（x）=fT（x）β+Z（x） （9）

式中：y（x）为待求函数;fT（x）β为回归模型;Z（x）为随机过程，其均值为0，方差为σ2，协方差为：

Cov（Z（xi），Z（xj））=σ2R（xi，xj），i，j=1…n（10）

式中：n为样本点;xi、xj为样本的分量;R（xi，xj）為相关函数。

假定已知样本S及其对应的响应值Y，则可以求得β和σ2的估计值如下：

=（FTR-1F）YFTR-1Y2=1n（Y-F）TR-1（Y-F） （11）

式中：S=［x1，x2，…，xn］;Y=［y1，y2，…，yn］;F为回归模型组成的向量;R为相关系数矩阵;分别表示为：

F=f1（x1）…fm（x1）f1（xn）…fm（xn） （12）

R=R（x1，x2）…R（x1，xn）R（xn，x1）…R（xn，xn） （13）

对任意点x，其估计值为：

（x）=fT（x）+r（x）R-1（Y-F） （14）

式中：（x）为估计值;r（x）为相关系数向量，可表示为：

r（x）=［R（x，x1），…，R（x，xn）］ （15）

2.2 时变系统地震易损性分析

系统地震易损性基于结构的整体损伤，并考虑整体结构在各构件的损伤状况和相互作用下的共同影响，对其抗震性能进行全面评估。本文桥梁系统地震易损性曲线基于联合概率地震需求模型方法［5］建立。

在分析过程中，需考虑氯离子侵蚀引起的材料性能退化的时变效应。因此，需建立不同构件概率地震需求模型。假定桥梁构件的地震需求服从对数正态分布，求得不同服役时间构件间的相关系数矩阵后，得到联合概率地震需求模型。由于考虑时变效应的地震易损性分析需要建立大量不同服役年限的有限元模型，因此采用高斯过程代理模型来简化地震易损性分析。在建立联合概率地震需求模型后，对地震需求和能力同时进行大量抽样，并记录抽样结果：

IF=1，其他0，［Sd1，Sd2，…，Sdn］<［SC1，SC2，…，SCn］（16）

式中：［Sd1，Sd2，…Sdn］为模型中的随机地震需求向量;［SC1，SC2，…，SCn］为模型中的随机地震能力向量。

对两者进行抽样后，可得结构特定损伤状态的失效概率Psys为：

Psys=∑Ni=1IFN （17）

式中：N为总抽样数。

上述时变系统地震易损性分析流程如图1所示。

3 桥梁工程实例

3.1 桥梁概况与有限元模型

本文所选桥梁为19.96 m+20.00 m+19.96 m的三跨连续梁桥（图2），桥面宽度为8.5 m，桥梁服役期为100年。主梁为三箱单室的预应力混凝土连

续箱梁，混凝土强度等级为C50;桥墩为实心圆形墩，混凝土强度等级为C30;桩基础为钻孔灌注桩;支座均为橡胶支座。

桥梁的非线性有限元模型基于OpenSees数值计算平台建立，桥梁的主梁和墩柱采用非线性梁柱单元模拟，桥面结构采用弹性梁柱单元模拟。橡胶支座采用双线性滞回模型模拟。桩径效应采用刚性连接单元模拟，桩-土的摩擦相互作用采用零长度单元模拟［12-13］。进行土体模拟时，砂土采用多屈服面塑性本构模型，可以模拟累积剪切变形和液化特性;黏土采用冯·米塞氏多屈服面运动塑性模型［14］，可以模拟非线性滞回材料。混凝土选用Concrete01材料，保护层混凝土的本构关系采用Kent-Scott-Park模型，核心混凝土的本构关系采用Mander模型;钢筋选用Steel02材料，普通钢筋的本构关系采用Giuffre-Menegotto-Pinto模型，预应力钢筋的本构关系采用带有初始应力的Giuffre-Menegotto-Pinto模型。土体材料参数如表1所列。建立的连续梁桥非线性有限元模型如图3所示。在该计算模型中，桥墩的保护层及核心混凝土与纵筋、箍筋协同工作，共同抵抗地震作用。在氯离子侵蚀作用下，保护层混凝土面积减小，抗压强度下降，随着服役时间增长，保护层混凝土开裂并钢筋逐步暴露，氯离子进一步侵蚀钢筋，钢筋面积及强度减小，从而减弱对核心混凝土的约束作用，核心混凝土的抗压强度下降。

3.2 侵蚀作用的时变效应

本文依据Oslakovic等［15］的研究结果，假定混凝土表面氯离子浓度为3 kg/m3。基于钢筋的点蚀模型，建立纵筋和箍筋的剩余面积时变曲线，如图4所示。

由图4可知：在桥梁服役期内，纵筋剩余面积近似呈线性下降，箍筋剩余面积在初期快速下降，中后期趋于平稳。

基于氯离子扩散和侵蚀机理，以及在氯离子侵蚀作用下桥墩钢筋混凝土材料的强度退化规律，可以分别建立钢筋和混凝土材料性能退化的时变曲线，如图5所示。其中，核心混凝土的抗压强度退化时变曲线基于混凝土本构的Mander模型并结合公式（7）计算得出。

由图5可知：在氯离子侵蚀作用下，桥墩钢筋锈蚀期间的屈服强度和极限强度退化趋势相似，随服役时间增加，纵筋强度呈现均匀线性下降;箍筋强度在服役中前期下降幅度较大，服役后期逐渐平稳。在钢筋锈蚀100年时，纵筋屈服强度下降幅度较小，极限强度下降幅度略大于屈服强度;箍筋屈服强度和极限强度相比纵筋下降幅度更大，最终强度均降为160 MPa左右。保护层混凝土和核心混凝土抗压强度退化趋势相似，在服役100年时，核心混凝土和保护层混凝土抗压强度下降幅度近似相等，最终稳定在某个强度。桥墩材料强度在服役四、五十年后明显退化，但是桥梁整体结构强度仍能满足一定期限内的正常使用条件。本文基于桥梁全寿命周期研究地震易损性，若服役后期桥梁无法满足正常使用功能要求，本文仍可为研究氯离子侵蚀作用下桥梁的使用寿命提供一定的理论依据。

3.3 损伤指标与时变极限状态

桥梁结构的损伤指标可采用相对位移延性比。桥墩的损伤等级分类如表2所列。

通过桥墩截面的弯矩-曲率分析可以获得桥墩的位移延性比损伤指标。弯矩-曲率分析能利用非线性材料的应力-应变关系准确表现钢筋混凝土截面的荷载-位移关系，从而有效评估截面的抗震性能。对桥墩截面按照每10年時间间隔进行弯矩-曲率分析，结果如图6所示。

由图6可知：在服役初期，桥墩截面所能承受的最大弯矩及对应的曲率较大，表明构件抗震性能较好;随着服役时间的增长，截面的最大弯矩和曲率不断降低，且服役初期至中期下降幅度较大;至服役100年时，相比于初期桥墩截面的最大弯矩和曲率大幅下降，表明构件的抗震性能随服役时间变化显著。

通过桥墩截面弯矩-曲率曲线可以求得桥墩位移延性比。由表2可知，为确定桥墩极限状态，需分别求得μcy1、μcy、μcy4和μcmax。其中μcy1=1，其余三项可按下式计算［16］：

μcy=ΔcyΔcy1

μcy4=Δc4Δcy1

μcmax=μcy4+3 （18）

式中：Δcy为墩顶等效屈服位移;Δc4为混凝土应变ε=0.004时的墩顶位移。

由上述公式并结合弯矩-曲率分析结果，可求得桥墩的时变极限状态参数如表3所列。

由上表可知：当桥墩极限状态采用位移延性系数来表示时，随着服役时间的增加，桥墩极限状态对应的损伤指标总体上缓慢减小，但在服役后期，相应的损伤指标略微增大。

由于只进行了桥墩截面弯矩-曲率分析，并得到了其时变极限状态，为求得桥梁结构系统易损性曲线，还需求不同构件之间的相关系数。由于氯离子侵蚀的时变效应影响造成桥墩抗震性能的退化，会影响构件之间的相关系数，故需考虑在不同服役年限下桥梁构件的相关系数变化。

基于系统地震易损性分析方法，在100年桥梁服役期内，以每10年为时间间隔，共建立11个连续梁桥有限元模型。求得各服役年限的桥梁构件间共11个相关系数矩阵，其中服役50年的矩阵如表4所列。

3.4 桥梁地震易损性分析

3.4.1 地震易损性曲线

桥梁地震易损性分析选用Median等［17］推荐的80条地震动。基于联合概率地震需求模型方法，采用高斯过程模型取代动力时程分析得到桥梁结构的动力响应，分别建立不同损伤状态下的桥梁时变系统地震易损性曲线，如图7所示。

由图7可知：在轻微损伤状态下，桥梁系统易损性随着服役年限增加没有明显变化;在其他三种损伤状态下，随着服役时间增加，桥梁结构系统损伤概率逐渐增大。在中等损伤状态下，桥梁系统易损性曲线在不同服役年限下间隔分布近似均匀，表明易损性随服役时间近似均匀增长;在另外两种高等级损伤状态下，桥梁系统易损性曲线间隔随着服役年限增长而变小，表明易损性在服役初期增长较快，在服役中后期增长变缓。随着损伤等级提高，不同服役年限的系统易损性曲线间隔逐渐增大。氯离子侵蚀作用对桥梁结构轻微损伤时的系统易损性几乎没有影响，但对桥梁结构高等级的损伤时的系统易损性影响较明显。考虑到系统易损性综合了桥墩构件的材料性能退化以及其他构件的相互影响，虽然桥墩的材料性能退化程度十分明显，但是桥梁系统的损伤超越概率的变化程度并不直接与之相关。

此外，为比较同一服役年限下桥梁结构不同损伤状态之间的关系，选择服役年限分别为0年、50年和100年三个时间点，绘制其不同损伤状态间的关系，如图8所示。

由图8可知：在服役初期，桥梁结构不同损伤状态间的地震易损性曲线分布较均匀，且曲线间隔较大;在服役中后期，不同损伤状态间的桥梁结构在同一服役年限时地震易损性曲线分布逐渐不均匀，且曲线间隔逐渐减小。表明在氯离子侵蚀作用下，随着服役年限的增长，桥梁地震易损性发生变化;桥梁结构在低等级损伤和高等级损伤状态下的失效概率差值不断减小，表明结构延性水平不断降低，抵抗损伤破坏的能力不断降低，桥梁更容易从低等级损伤状态进入高等级损伤状态。

3.4.2 地震易损性曲面

以每10年为时间间隔建立的桥梁地震易损性曲线无法反映桥梁在任意年限时的抗震能力，因此，为了全面反映桥梁抗震性能的逐年变化，基于高斯过程模型，建立不同损伤状态下的桥梁损伤超越概率与服役时间t、地震动峰值加速度PGA的关系，即桥梁系统地震易损性曲面，如图9所示。

综合图7和图9可知：在轻微损伤状态下，桥梁系统地震易损性曲线在不同服役年限下几乎重合，表明桥梁系统地震易损性几乎不随服役时间改变;在中等损伤状态下，桥梁时变系统易损性曲面随着PGA增大和服役时间增加变化相对平滑，表明PGA和服役时间对桥梁易损性的影响较小;而在严重损伤和完全损伤状态下，随着PGA增大和服役时间增加，桥梁损伤概率相比服役初期显著提高，桥梁地震易损性受到明显影响。

4 结论

（1） 模拟并计算了氯离子侵蚀作用对桥梁构件材料性能退化的影响，得到桥墩钢筋混凝土材料的性能退化时变曲线。结果表明：在氯离子侵蚀作用下，100年桥梁服役期内的纵筋强度大致呈线性下降，箍筋强度在服役初期至中期快速降低，服役中后期逐渐稳定，箍筋强度与纵筋强度相比下降幅度更大;核心混凝土和保护层混凝土强度退化趋势相似，均是服役前期强度快速降低，服役中后期强度下降速率逐渐变慢直至平稳。

（2） 研究了氯離子侵蚀作用对桥梁地震易损性的影响，得到桥梁时变系统地震易损性曲线和曲面。结果表明：在氯离子侵蚀作用下，桥梁轻微损伤状态下的时变地震易损性结果几乎不变，对另外三种高等级损伤状态下的地震易损性结果产生较大影响，且损伤等级越高，易损性变化越明显。桥梁整体延性性能随服役时间增加而不断下降，桥梁结构在地震作用下更倾向于发生高等级的损伤。

结论表明，对于处在侵蚀环境下的桥梁结构，其抗震性能随服役时间变化显著，在进行地震易损性分析时应考虑时变效应。

参考文献（References）

［1］ STEWART M G.Mechanical behaviour of pitting corrosion of flexural and shear reinforcement and its effect on structural reliability of corroding RC beams［J］.Structural Safety，2009，31（1）：19-30.

［2］ KUMAR R，GARDONI P，SANCHEZ-SILVA M.Effect of cumulative seismic damage and corrosion on the life-cycle cost of reinforced concrete bridges［J］.Earthquake Engineering & Structural Dynamics，2009，38（7）：887-905.

［3］ 李磊，郑山锁，周宁.锈蚀RC柱性能化抗震能力的评价模型［J］.土木工程学报，2013，46（增刊2）：50-56.

LI Lei，ZHENG Shansuo，ZHOU Ning.Performance-based comprehensive evaluation on the seismic behavior of the corroded RC column［J］.China Civil Engineering Journal，2013，46（Suppl02）：50-56.

［4］ 赵珺，牛荻涛.在役钢筋混凝土连续刚构桥梁抗震性能评估［J］.中国公路学报，2014，27（9）：74-81.

ZHAO Jun，NIU Ditao.Seismic performance evaluation for reinforced concrete continuous rigid frame bridge in service［J］.China Journal of Highway and Transport，2014，27（9）：74-81.

［5］ NIELSON B G.Analytical fragility curves for highway bridges in moderate seismic zones［D］.Atlanta，GA：Georgia Institute of Technology，2005.

［6］ WAN H P，REN W X.Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process metamodel［J］.Journal of Structural Engineering，2015，141（6）：04014164.

［7］ WAN H P，REN W X.Stochastic model updating utilizing Bayesian approach and Gaussian process model［J］.Mechanical Systems and Signal Processing，2016，70：245-268.

［8］ COLLEPARDI M，MARCIALIS A，TURRIZIANI R.Penetration of chloride ions into cement pastes and concretes［J］.Journal of the American Ceramic Society，1972，55（10）：534-535.

［9］ VAL D V，MELCHERS R E.Reliability of deteriorating RC slab bridges［J］.Journal of Structural Engineering，1997，123（12）：1638-1644.

［10］ STEWART M G，AL-HARTHY A.Pitting corrosion and structural reliability of corroding RC structures：experimental data and probabilistic analysis［J］.Reliability Engineering & System Safety，2008，93（3）：373-382.

［11］ CORONELLI D，GAMBAROVA P.Structural assessment of corroded reinforced concrete beams：modeling guidelines［J］.Journal of Structural Engineering，2004，130（8）：1214-1224.

［12］ WAN H P，SU L，FRANGOPOL D M，et al.Seismic response of a bridge crossing a canyon to near-fault acceleration-pulse ground motions［J］.Journal of Bridge Engineering，2021，26（6）：05021006.

［13］ 万华平，卫志成，苏雷，等.基于系统地震易损性的桥梁隔震支座优化设计［J］.地震工程与工程振动，2021，41（5）：69-78.

WAN Huaping，WEI Zhicheng，SU Lei，et al.Optimal design of seismic isolation bearings of bridge based on system seismic fragility［J］.Earthquake Engineering and Engineering Dynamics，2021，41（5）：69-78.

［14］ 苏雷.液化侧向扩展场地桩-土体系地震模拟反应分析［D］.哈尔滨：哈尔滨工业大学，2016.

SU Lei.Earthquake simulation response of soil-pile system in liquefaction-induced lateral spreading ground［D］.Harbin：Harbin Institute of Technology，2016.

［15］ STIPANOVIC OSLAKOVIC I，BJEGOVIC D，MIKULIC D.Evaluation of service life design models on concrete structures exposed to marine environment［J］.Materials and Structures，2010，43（10）：1397-1412.

［16］ 张菊辉.基于数值模拟的規则梁桥墩柱的地震易损性分析［D］.上海：同济大学，2006.

ZHANG Juhui.Seismic vulnerability analysis of regular beam pier column based on numerical simulation［D］.Shanghai：Tongji University，2006.

［17］ MEDINA R，KRAWINKLER H.Seismic demands for nondeteriorating frame structures and their dependence on ground motions［R］.Stanford，USA：the John A Blume Earthquake Engineering Center，Stanford University，2003.

（本文编辑：任 栋）

基金项目：国家重点研发计划（2021YFF0501001）;浙江省重点研发计划（2021C03154）;国家自然科学基金（51878235，42072310）

第一作者简介：万华平（1986-），男，研究员，博士生导师，主要从事结构健康监测和结构不确定性分析方面研究。E-mail：hpwan@zju.edu.cn。

通信作者：苏 雷（1986-），男，教授，博士生导师，主要从事土动力学与岩土地震工程方面研究。E-mail：sulei@qut.edu.cn。

万华平，彭紫鑫，卫志成，等.基于高斯过程模型的桥梁时变系统地震易损性分析［J］.地震工程学报，2024，46（3）：511-520.DOI：10.20000/j.1000-0844.20220824004

WAN Huaping，PENG Zixin，WEI Zhicheng，et al.Seismic fragility analysis of the time-varying system of a bridge with a Gaussian process model［J］.China Earthquake Engineering Journal，2024，46（3）：511-520.DOI：10.20000/j.1000-0844.20220824004