基于深度强化学习分层控制的双足机器人多模式步态系统研究

徐毓松 上官倩芡 安康

摘  要： 提出一种基于深度强化学習（DRL）分层控制的双足机器人多模式步态生成系统. 首先采用优势型演员-评论家框架作为高级控制策略，引入近端策略优化（PPO）算法、课程学习（CL）思想对策略进行优化，设计比例-微分（PD）控制器为低级控制器；然后定义机器人观测和动作空间进行策略参数化，并根据对称双足行走步态周期性的特点，设计步态周期奖励函数和步进函数；最后通过生成足迹序列，设计多模式任务场景，并在Mujoco仿真平台下验证方法的可行性. 结果表明，本方法能够有效提高双足机器人在复杂环境下行走的稳定性以及泛化性.

关键词： 双足机器人； 步态规划； 近端策略优化（PPO）； 多模式任务； 课程学习（CL）

中图分类号： TP 18    文献标志码： A    文章编号： 1000-5137（2024）02-0260-08

Research on multi-mode gait hierarchical control system of biped robot based on hierarchical control of deep reinforcement learning

XU Yusong， SHANGGUAN Qianqian^?， AN Kang^?

（College of Information， Mechanical and Electrical Engineering， Shanghai Normal University， Shanghai 201418， China）

Abstract： According to the current research in the application of bipedal robot gait control， there still existed deficiency and challenge related to stability and generalization in complex scenarios. A multi-mode bipedal robot gait generation system based on hierarchical control using deep reinforcement learning （DRL） was proposed. Initially， an advantage-actor-critic framework was employed as the high-level control strategy， integrating proximal policy optimization （PPO） algorithm and the concept of curriculum learning （CL） to optimize the policy. A proportional-differential （PD） controller was designed as the low-level controller. Next， the robot's observation and action spaces were defined for policy parameterization. Leveraging the cyclic nature of symmetric bipedal walking gaits， a gait cycle reward function and stepping function were devised. Finally， by generating footstep sequences， multiple-mode task scenarios were formulated， and the feasibility of the method was validated using the Mujoco simulation platform. The results demonstrated that the improved approach effectively enhanced the stability and generalization of bipedal robot walking in complex environments.

Key words： bipedal robot； gait planning； proximal policy optimization（PPO）； multimodal task； course learning（CL）

深度强化学习（DRL）结合了深度学习强大的数据处理以及强化学习交互决策的能力，是解决双足机器人步态控制的重要思路. ZHAO等^［1］利用深度Q网络（DQN）算法解决了非平整地面上双足机器人的稳态控制问题，但DQN只适用于离散和低维动作空间，限制了其处理连续和高维动作空间的能力.KUMAR等^［2］采用深度确定性策略梯度（DDPG）算法规划双足机器人的步态，实验结果显示，控制效果良好. 但DDPG算法可能引起过高估计价值的问题，这种估计误差可能随时间累积，影响策略更新的质量. 在复杂环境下双足机器人的步态控制需要更加稳定和高效的策略算法，近端策略优化（PPO）^［3］基于策略梯度（PG）^［4］算法和演员-评论家^［5］框架，对策略更新方式进行了优化，拥有更强的稳健性和收敛性，并能很好地适用于双足机器人连续动作的场景，使其成为目前解决双足机器人步行控制问题最常用的DRL算法之一.

本文作者采用近PPO算法，解决算法策略更新质量差，以及无法处理连续高维动作空间场景的问题. 加入课程学习的训练思想，解决算法易陷入局部最大值的问题，并设计多模式任务对双足机器人进行步行控制，解决算法策略泛化性差的问题. 最终的实验结果表明：本方法能够使机器人在单一策略下完成上下阶梯、不平整路面、转弯、后退等多种模式的步行任务，具有较强的稳定性和泛化性.

1  DRL策略架构

1.1 优势型演员-评论家框架

强化学习方法可分为基于值和基于策略两类. 基于值的算法能够在每一步都进行策略更新，提高了效率，但仅适用于处理小规模的离散问题. 而对于处理状态与动作空间庞大，甚至连续无限的情况，策略梯度法更有优势，但其策略参数每回合更新一次，学习效率较低. 演员-评论家框架则将这两类算法的优势相结合，既能处理连续状态与动作空间的问题，又具有每步更新策略的能力.在此基础上，优势型演员-评论家算法使用Advantage函数来估计动作的优劣，相对于Aho-Corasick（AC）算法，Advantage函数考虑每个动作相对于平均动作的优势，有助于减少训练过程中的方差，使训练更加稳定，同时更准确地评估动作的价值，提高学习效率.

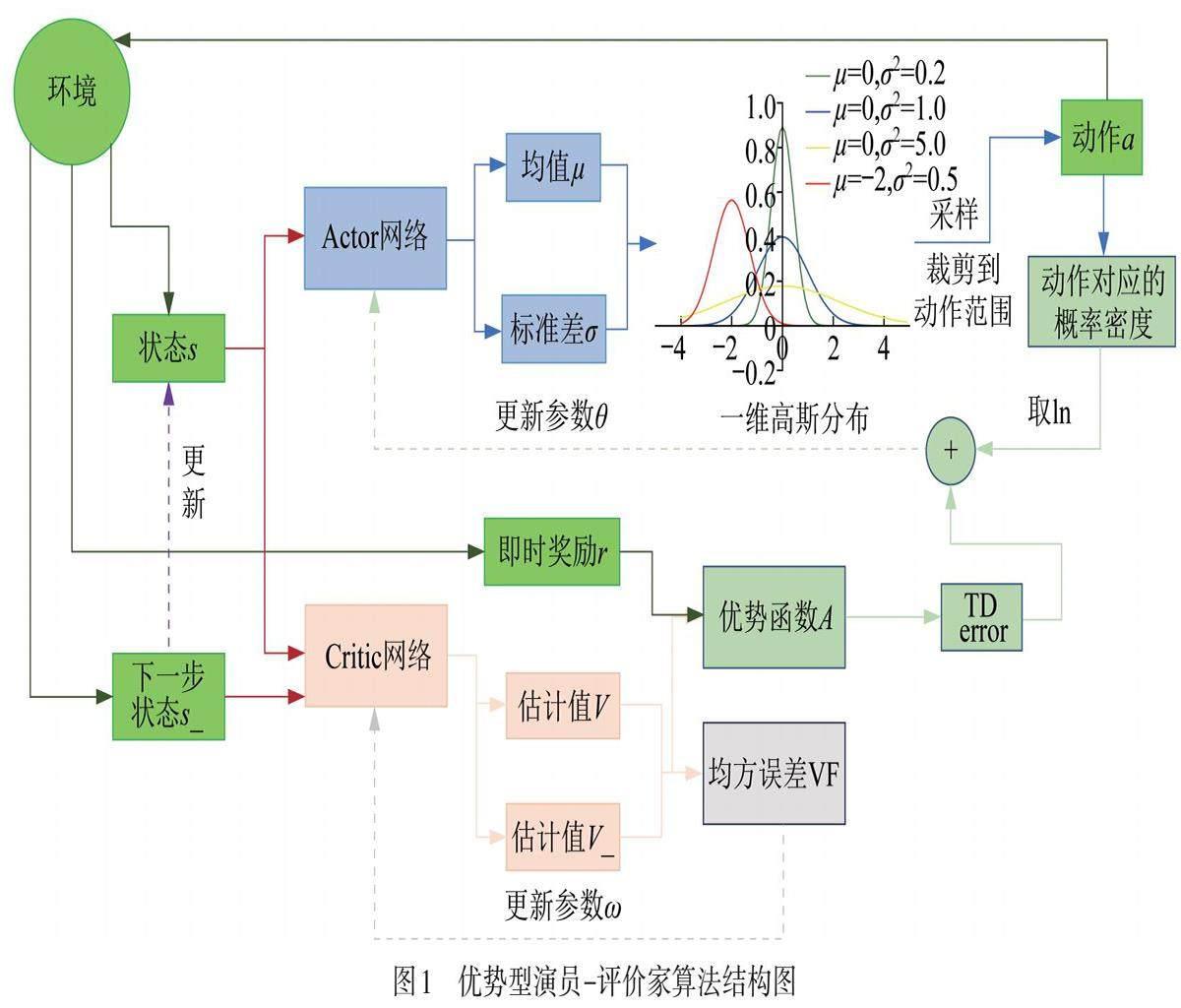
首先，将初始状态s输入actor网络，产生均值u和标准差σ，构建一个高斯分布. 然后从中采样，将样本的横坐标值进行裁减，输出最后的动作action. action和环境交互，产生新的状态s_和即时奖励r，将s和s_分别输入critic网络，分别输出价值和估计值v和v_. 通过v，v_和r构成优势函数，再近似成时序差分（TD）误差，结合action的概率分布，更新actor网络的参数，而critic網络通过v和v_的均方误差更新自身参数. 最后，使用s_更新s，进行新一轮训练.

1.2 PPO算法

策略梯度方法在更新策略参数时，学习率设定过大，可能导致策略过快更新，难以收敛；学习率设定过小，则会使学习进展缓慢. Actor-Critic框架使用同一策略进行采样和实时更新，使得每次采样的数据只能被单次使用，效率较低. PPO算法克服了这些问题，其核心思想是近端优化，并结合重要性采样和策略裁剪来保证训练的稳定性和收敛性，使得模型能够学习到更好的策略. 通过在每次更新中PPO算法对策略进行小步长的改变，以确保新的策略不会与旧的策略相差太远，有助于防止训练中出现不稳定性；在计算策略更新时，PPO算法使用重要性采样来估计新旧策略之间的差异，比较新策略与旧策略在样本上的表现，以确定是否接受该次更新.

1.3 课程学习思想

传统的强化学习训练可能面临以下问题：（1） 复杂任务下，随机初始化的智能体难以获得有效的奖励信号，导致学习缓慢；（2） 直接从难度较高的环境开始训练可能使模型运行困难，难以学习有效策略. 在DRL中，课程学习是一种训练策略，将学习任务分解为递增难度的阶段，以解决上述问题.

为实现机器人在复杂环境，如阶梯、不平整路面下保持稳定步态，采用关于样本分布的课程. 首先策略只运用于平面序列，即手动生成的足迹序列和规划器生成的弯曲路径. 然后经过M次迭代后，将台阶的高度从0米线性提高或降低h米，继续迭代N次，阶梯高度P与训练迭代次数i的关系如下：

（1）

其中，k＝｛-1，1｝，k＝-1表示台阶高度下降，k＝1表示台阶高度上升.

2  基于DRL的分层控制架构设计流程

2.1 分层控制框架设计

分层控制框架包括一个高级别强化学习（RL）策略以及一个1 000 Hz的低级别比例-微分（PD）控制器.RL策略以40 Hz缓慢地更新关节位置，PD控制器将期望的关节位置转换为关节扭矩.由于PD控制器使用相对较低的增益，预测位置的误差可能非常大，而RL策略利用其中的跟踪误差来产生作用力，驱使机器人前进^［6］. PD控制器与负责向RL策略提供所需足迹和机器人根部航向的足部序列生成器协同工作，理想情况下，足部序列生成器将依靠对环境有效的感知，为机器人动态规划路径分级控制结构概述如图2所示.

RL策略的输入是将要执行的两个计划足迹、时钟信号和机器人状态，通过传统方法进行足迹规划，即交替性规划左右脚足迹的步长、步宽及步高.RL策略做出的预测结果被添加到中性运动位置（偏置），发送到PD控制回路.

2.2 DRL策略架构参数化

为了让DRL策略架构应用在双足机器人上，需要定义观测空间即机器人的内部和外部状态，以及时钟信号作为RL策略能够感知的输入参数，同时定义机器人各个关节组成的动作空间作为RL策略的输出参数.

观测空间包括了机器人的内部状态、外部状态和时钟信号，其中内部状态包括了每个致动关节的位置和速度（仅在腿部）、滚转和俯仰方向以及根部（骨盆）的角速度. 外部状态包括了两个即将执行的足迹数据的3D位置和1D航向描述. 时钟信号用于后续的周期奖励，可以由循环相位变量的单个标量表示，该循环相位变量每个时间步长从0递增到1，也可以将投影到2D单位周期，

， （2）

其中，L是重置為0之后的周期. 这种投影是为了防止时钟输入在每个周期结束时从1突然跳变到0，导致系统不平稳的情况.

动作的空间包括机器人腿被致动关节（只考虑下半身的12个）的期望位置. 来自策略的期望关节位置预测结果在被发送到较低级别的PD控制器之前，会被添加到与机器人的半坐姿相对应的固定马达偏移中.

2.3 DRL策略架构奖励函数设计

强化学习通过最大化奖励来更新模型参数，进而控制双足机器人稳定行走，故奖励函数的设计至关重要.

本文按照SIEKMANN^［7］提出的周期性奖励组合的思想，将一个步态周期分为单脚支撑（SS）和双脚支撑（DS）阶段，如图3所示. 在上半步态周期中，DS阶段双脚均触底（右脚在前，左脚在后），SS阶段右脚与地面静态接触作为支撑脚，而左脚在空中摆动作为摆动脚. 在下半周期中左脚转变为支撑脚，右脚转变为摆动脚，周而复始.

调节脚部地面反作用力的奖励项和速度，计算如下：

（3）

其中，，，分别是左右脚调节地面反作用力和速度的相位函数. 在SS阶段，函数I  ∈ ［-1，1］激励摆动脚的速度，惩罚摆动脚的地面反作用力，同时惩罚支撑脚的速度，并激励支撑脚的地面反作用力；在DS阶段，正好相反. 将机器人在SS及DS阶段的持续时间分别设置为0.8 s和0.2 s. 当位于步态周期的第一个单支撑区域时，接近于-1，而则接近于1，表明的较大值会得到负回报，而的较大值则会得到正回报，即左脚在摆动，右脚提供支撑.

除了周期性奖励外，还需要激励机器人根据预设的目标位置对身体进行步进和定向. 步进函数可以划分为命中奖励和进度奖励. 命中奖励的作用是促使机器人将任意一只脚放在即将到来的目标点上，只有当其中一只脚或者两只脚在目标半径内，才会触发这个奖励机制.

假设为目标足迹和与足迹邻近脚的距离，为目标足迹和根部的距离，则步进奖励

， （4）

其中，，是可調节的超参数. 根方向项鼓励四元数接近期望的四元数，四元数是由0°的滚转角、0°的俯仰角和一定角度偏航角组成的欧拉角，

（5）

其中，表示的内积.

2.4 多模式任务设计

多模式任务的设计主要通过足迹序列规划器实现. 足迹由一个3D点组成，该点附有一个航向矢量（），分别表示脚放置的目标位置和机器人躯干的目标偏航方向. 通过将“航向矢量”附加到足迹上，可以实现机器人多模式步态生成.

向前行走的足迹计划通过交替定义机器人步长、步宽、步高而生成，通过在线段的左右交替放置点，从机器人根部在地板上的投影开始，向前延伸. 同理，对于向后行走，可以通过将点放置在向后方延伸的线段左侧和右侧来生成平面；对于原地站立，轨迹仅由原点处的1步组成；对于横向行走，将步长转换到纵轴方向；对于在弯曲路径上行走，使用Humanoid Navigation ROS软件包^［8］中的足迹规划器生成足迹，该软件包实现了基于搜索的规划器；对于上楼与下楼，通过设置固定的步高实现，步高根据课程学习参数设定，同时设置阶梯的高度随步高变化，楼梯梯段固定等于台阶长度，以确保观察到的目标台阶正好位于楼梯梯段的中间；对于不平整阶梯行走，通过对步态高度进行方向和高度的正负交替变化生成足迹.

3  引入课程学习的多模式任务实验与讨论

3.1 多模式任务实验

本实验设置actor和critic网络都为多层感知（MLP）架构，包含两个各含有256个神经元的隐藏层，使用ReLu作为激活函数. 为了限制参与者预测的范围，策略的输出通过TanH层传递. 将训练迭代次数设置为20 000次，每个PPO的推出长度为400个时间步长，即机器人一个回合的长度，每个训练批次包含64个回合. 学习率设置为0.000 1，其他超参数设置参考文献［7］.

多模式任务包括斜走、站立、后退、横走和前进模式，分别以［0.15， 0.05， 0.20， 0.30， 0.30］的概率在每次训练回合中出现. 前进模式下，机器人的步行高度方向及上下楼均为随机变化. 此外，随机化机器人的初始相位以及关节噪声来增加策略的探索能力. 最后，将模型导入Mujoco仿真器中，并在JVRC_1^［9］机器人上进行训练，JVRC_1是一款为虚拟环境设计的机器人，身高1.72 m，体重62 kg，本研究冻结其除髋、膝、踝之外的其他关节.

斜走模式通過随机选取Humanoid Navigation ROS软件包生成的足迹，如图4所示. 横走模式只规划y方向上的目标位置，大步长和小步长交替循环，且随机化初始方向，如图5所示. 前进模式包括上楼和下楼两个场景，通过随机化目标位置高度及方向，实现两个场景的初始化. 通过递增目标位置高度，设置20格阶梯，随机化前两个或三个阶梯高度，并保持不变，即目标位置高度不变.通过课程学习的参数设定步高，最大为0.1 m，如图6所示.

3.2 引入课程学习对策略效果影响的对比实验

为了增强策略的学习效果，避免策略因为陷入局部最优而无法达到目标训练效果的困境，引入课程学习技术. 多模式场景下，除前进模式外，机器人都是在水平面且无障碍物情况下步行，无需使用课程学习. 而在前进模式下，如果阶梯的高度过高，即使有步进奖励函数的激励，也无法保证机器人在每一回合训练中都能脱离平面步行状态，调整自身关节角度和重心变化，迈上阶梯. 一旦机器人倒地，会触发奖惩机制，导致总奖励变少. 此时，策略会在每个时间步内都选择原地踏步来避免总体奖励减少，易陷入局部最优.

对策略不使用课程学习进行训练，并让机器人在阶梯高度为0.3 m的场景下行走，实验结果如图7所示，机器人在面对台阶时并未有抬脚动作，而是原地踏步.

为进一步检验算法对机器人的极限泛化能力，将阶梯高度提升到0.3 m（接近关节电机驱动能力的极限），对该场景加入课程学习进行迭代训练，如图8所示.

比较两次实验策略在每回合的奖励以及时间步长，得到训练过程的评估图，如图9～10所示.策略训练评估以100次为频率，横轴为迭代次数，左侧纵轴为回合总奖励，右侧纵轴为回合长度.

对策略加入课程学习进行训练，算法在执行3 000次迭代后，可达到收敛状态，回合奖励稳定在250～300.

根据对比实验可知，对于多模态步态控制方法，加入课程学习有利于算法探索复杂场景，同时因为课程学习是在训练周期中逐步提升阶梯高度，使得机器人在最大阶梯高度之内的随机阶梯高度下，都能正常稳定地行走，也提升了方法的泛化能力.

4  结语

针对现阶段双足机器人使用DRL进行步态规划仍存在的稳定性、泛化性不足的问题，本文作者提出一种基于DRL算法，采用分层控制框架进行双足机器人步态的生成，同时针对复杂环境设计多模式任务，在Mujoco仿真平台上使用JVRC_1机器人验证了该方法的可行性和稳定性. 根据双足机器人步行周期性的规律，使用步态周期奖励和步进奖励提升策略学习效率和稳定性；为验证方法在多任务下的稳定性，设计包括前进、后退、横走、斜行、站立、上下楼及不平整阶梯场景为一体的多模式任务用于策略学习，并得到稳定的实验效果；为了避免策略在多模式下学习陷入局部最优，引入课程学习思想，将学习任务分解为递增难度的阶段，让机器人稳定学习.通过对比实验，证明了在各种复杂环境下，本方法能有效提高双足机器人稳定行走的能力，使其具有较强的泛化性和稳健性，为DRL在双足机器人步行控制领域的应用提供了新的思路. 然而，如何进一步提升算法的效率、稳定性、可迁移性都是本研究需要逐步完善的方面.

参考文献：

［1］ ZHAO Y T， HAN B， LUO Q. Walking stability control method based on deep Q-network for biped robot on uneven ground ［J］. Journal of Computer Applications， 2018，38（9）：2459.

［2］ KUMAR A， PAUL N， OMKAR S N. Bipedal walking robot using deep deterministic policy gradient ［J/OL］. arXiv， 2018［2023-12-01］. https： //arxiv.org/abs/1807.05924.

［3］ SCHULMAN J， WOLSKI F， DHARIWAL P， et al. Proximal policy optimization algorithms ［J/OL］. arXiv， 2017［2023-12-01］. https： //arxiv.org/abs/1707.06347.

［4］ SUTTON R S， MCALLESTER D， SINGH S， et al. Policy gradient methods for reinforcement learning with function approximation ［C］// Proceedings of the 12th International Conference on Neural Information Processing Systems.Cambridge： ACM， 1999：1057-1063.

［5］ KONDA V， TSITSIKLIS J. Actor-critic algorithms［J］. Advances in Neural Information Processing Systems， 1999，12：4-6.

［6］ HWANGBO J， LEE J， DOSOVITSKIY A， et al. Learning agile and dynamic motor skills for legged robots ［J］. Science Robotics， 2019，4（26）：9-12.

［7］ SIEKMANN J， GODSE Y， FERN A， et al.Sim-to-real learning of all common bipedal gaits via periodic reward composition ［C］// IEEE International Conference on Robotics and Automation. Xi'an：IEEE， 2021： 7309-7315.

［8］ HORNUNG A， DORNBUSH A， LIKHACHEV M， et al. Anytime search-based footstep planning with suboptimality bounds［C］// 12th IEEE-RAS International Conference on Humanoid Robots. Osaka： IEEE， 2012：674-679.

［9］ OKUGAWA M， OOGANE K， SHIMIZU M， et al.Proposal of inspection and rescue tasks for tunnel disasters：task development of Japan virtual robotics challenge ［C］// IEEE International Symposium on Safety， Security， and Rescue Robotics. West Lafayette： IEEE， 2015：1-2.

（责任编辑：包震宇，顾浩然）

DOI： 10.3969/J.ISSN.1000-5137.2024.02.018

收稿日期： 2023-12-23

作者简介： 徐毓松（1999—）， 男， 硕士研究生， 主要从事双足机器人方面的研究. E?mail： 1000513417@smail.shnu.edu.cn

* 通信作者： 上官倩芡（1976—）， 女， 副教授， 主要从事人工智能方面的研究. E?mail： shangguan@shnu.edu.cn；安康（1981—）， 男， 副教授， 主要从事双足机器人方面的研究. E?mail： ankang@shnu.edu.cn

引用格式： 徐毓松， 上官倩芡， 安康. 基于深度强化学习分层控制的双足机器人多模式步态系统研究 ［J］. 上海师范大学学报 （自然科学版中英文）， 2024，53（2）：260?267.

Citation format： XU Y S， SHANGGUAN Q Q， AN K. Research on multi-mode gait hierarchical control system for bipedal robot based on deep reinforcement learning ［J］. Journal of Shanghai Normal University （Natural Sciences）， 2024，53（2）：260?267.