借助情境构建高效数学课堂
2024-05-30曾凤英
曾凤英

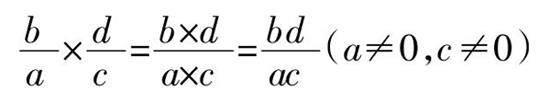
“分数乘分数”是人教版六年级上册数学第一单元的内容,属于代数部分的重点内容。这部分需要用到前期所学的“一个数乘几分之几,表示的是求这个数的几分之几是多少”这一知识点,从这个角度来理解分数算理也比较抽象,所以教师需引导学生借助情境直观来理解“分数乘分数”的算法。
一、教法研究
很多学生对“分数乘分数”内容的理解处于浅表化状态。因为小学阶段学生的思维以具象为主,核心素养的表现侧重于意识,即基于经验的感悟。如果没有具体情境体验就不会有真正的数学眼光,为此“分数乘分数”部分的教法研究着眼于以下几方面:第一,构建情境模型,发展学生的算理探究意识,将数形结合与逻辑推理有机关联在一起,先让学生探索用整数来计算长方形的面积,接着将问题案例中的整数替换为分数,让学生进一步思考遇到分数乘分数的问题。第二,运用数形结合,引导学生动手操作实践,如通过折纸、拼贴、裁剪等多个渠道来验证算理,进一步让学生归纳出“分数乘分数”计算的通用公式。第三,提高学生对“分数乘分数”运算法则的应用意识,即结合具体问题,让学生探索如何根据问题情境来构建模型,列出算式,探究算理,最后对结果的真实性进行验证。
二、课例呈现
▲第一环节:课前预热,温故知新
1.看图说分数
教师通过大屏幕上出示图片(见图1),让学生说一说图中阴影部分应该用分数怎样来表示。
(设计意图:“分数乘分数”与前面学生所学的“整数乘分数”密切相关,所以教学中教师可先通过旧知识导入,为学生学习新知识做好有效铺垫。)
2.按照要求画分数
用你喜欢的颜色涂一涂(见图2)。
(设计意图:通过图画的方式,进一步巩固学生对分数的认识,为下一步学生理解“分数乘分数”算理奠定基础。)
3.结合问题用分数
有一块100平方米的地,李伯伯将这块地的9/10用来种土豆,1/10用来种玉米,李伯伯种土豆的面积是多少?种玉米的面积是多少?
(设计意图:结合土豆、玉米面积的计算,巩固“整数乘分数”的算法,综合对乘法的意义、分数的意义进行回顾。)
归纳:求一个数的几分之几可以用该数乘以相应的分数来计算。整数乘分数时,整数与分子去相乘,分母不变,能约分的要先约分。
▲第二环节:导出新知,算理探究
结合前面的例题,稍作变動就可以引出一个新问题:
李伯伯家有1/2公顷土地,他想用这块地的9/10来种植土豆,再用其中1/10来种植玉米,请问李伯伯种植土豆的面积是多少公顷?种植玉米的面积是多少公顷?
通过对题意的分析,学生能发现新问题与前面的问题一脉相承,原来的土地面积为100平方米,到了新问题中,变成1/2公顷,而土豆和玉米种植所占比例完全不变,所以学生很容易就能列出算式,接着就需要让学生对“分数乘分数”的算法进行探究。
明确了需要解决的问题后,教师可以启发学生动手实践,实现问题突破。有的学生想到了把分数变成小数:1/2×9/10=0.5×0.9=0.45(公顷)
教师可以先肯定学生的想法,接着启发学生进一步思考,该问题中碰到的分数可以转化成小数,如果下次碰到1/2,3/7这类不能转化成小数的分数,又该如何计算?
这时,结合前面对分数表示方法的回顾,教师可引导学生通过画图的方式来呈现算式:1/2×9/10,学生通过画格子,将一整张纸等分为100份,横向选取其中5行,记作5/10,纵向选取其中9列,记作9/10,在两者相交的格子部分涂上颜色,就是最后求出的结果,即45/100。
结合学生绘制的图形,教师让学生说一说,算式中每一个数在图中分别代表哪些含义,结果中的100如何得来,横向的10格和纵向10格分别代表了什么意思。学生结合自己对题目的理解指出,在这里将一个正方形平均分成了100份,横向选取其中5行,代表了原题中的1/2。纵向选取5行中的9列,代表了已经选中部分的9/10。也就是求这个数的9/10,即求这个图形的9/10占多少格,经过计算得出占45格。
(设计意图:本环节结合图形的绘制,让学生来说算理,从而可以发现分数的计算就是分子和分子相乘来做分子,分母和分母相乘来做分母,初步探索得出计算“分数乘分数”的方法。)
在画图的基础上,还有学生探索出了用折纸的方法来呈现结果。学生取出一张小纸条,将其竖折等分为10份,选择其中9份,接着将纸张横向对折,即两等分,取其中一半,即为结果9/20。通过这样的方式,学生也明白了把一个长格平均分成10份,其中9份就是9/10公顷,再横向对折选取其中1/2,得到的最后结果就是9/20公顷。学生这样计算的过程,就相当于把原来的1公顷平均分成10份,其中的9份就是9/10公顷,9/10公顷乘1/2,得到最后结果为9/20公顷,这样的结果更加简洁明了。
而在这步探索的过程中,学生发现了一些新问题,45/100与9/20大小相等,但是不同的两种表示方法,那么在最后结果呈现时,用哪个数据更恰当?
这里就涉及分数计算的另一个注意事项,就是能约分的先约分。在分数计算过程中,如果只是单纯的分子乘分子、分母乘分母,可能导致最后计算运算量加大。针对这一问题,在计算的过程中,教师需要引导学生能约分的先约分,化简为最简分数。这样能提高计算准确率,也能降低学生计算的难度。
▲第三环节:小组合作,知识迁移
借助案例,让学生理解分数乘分数的算法,学生掌握得并不扎实。教师可在大屏幕出示类似的练习,让学生以小组为单位进行讨论分析。最后再让各个小组呈现自己的计算结果,尝试回顾探究过程,进行算理解释。通过反复练习,学生对分数乘法的意义有效理解并熟练掌握计算“分数乘分数”的正确方法。
在此基础上,教师可引导学生在小组内部讨论分数乘分数的算式如何用字母来表示,进而得出结论。
▲第四环节:算法应用,练习巩固
小学数学要体现教学做合一育人,“分数乘分数”部分学习完成后,教师也要让学生及时练习,有效巩固,完成教材中的习题,要求学生运用所学的计算方法,准确熟练地计算,并让学生完成教材第6页的第4、5题,说出列式的依据及自己的计算方法。
例题当堂试练部分,教师要重点结合学生出错的问题进行有效解析。先让学生在小组内部进行讨论,探索问题解答的正确方式,由班里掌握较好的学生对其他同学进行指导,教师观察学生的思维盲点,可引导学生有效互助。结合出错的问题,让学生高效订正,也能让学生明白自己错在哪里,实现针对性提升。尤其是涉及约分的题目,有的学生会忽略分子、分母需同时约分,造成答案错误。
教师还可以通过大屏幕为学生出示一些延伸例题,让学生进行对比分析。
(设计意图:学习新知识后,教师要引导学生通过课后练习,做好及时巩固,这是检验学生学习成果,促进学生扎实掌握的有效步骤。后续补充练习中,加法和乘法同时出现是为了培养学生良好的观察意识,引导学生梳理分析的有效方式。在新知识学习后,学生对前期所学知识容易遗忘。这种针对性练习,可以让学生进一步回顾前期所学的通分方法,并有效区分分数加法和分数乘法的计算,让学生扎实理解分数计算方法的多样性,并为后续运算律的学习做好铺垫。)
▲第五环节:思维延伸,巧学趣练
在完成教材内容的前提下,教师还可以为学生出示一些判断、填空、简答等问题,让学生试着说一说,进一步拓展学生学习视野,达成核心素养育人目标。
1.判断题
(1)一个数(零除外)乘真分数积一定小于这个数。( )
(2)1米的1/2和5米的1/5一樣长。( )
(3)1小时的1/2和半小时一样长。( )
2.填空题
(1)分数乘分数时,用( )相乘的积做( ),用( )相乘的积做( )。
(2)分数乘分数时,能( )的先( ),再计算会更简便。约分时,一般不在( )上约分,计算结果一般是( )。
3.延伸拓展题
我国古代著名哲学著作《庄子·天下》有云:“一尺之锤,日取其半,万世不竭。”你能试着说一说这句话的意思吗?能不能用今天所学的分数的知识来解释,其中蕴含的哲理。
(设计意图:思维延伸部分是在教材教学基础上融合核心素养理念所提炼的一些综合性问题,其中既涉及了算理的理解,还涉及多元综合知识,如长度的比较、时间的计算,这些与前期学生所学知识紧密关联,同时也涉及分数的计算。最后的延伸阅读涉及了传统文化中与分数相关的阅读资料,其中蕴含的哲理非常丰富。小学生了解这类内容,能增强其文化自信,也能让其初步理解极限的概念,为其中学阶段的知识学习奠定良好基础。)
三、教学反思
“分数乘分数”是发展学生运算能力、引导学生理解算理、掌握正确算法、进行数据转化处理的重要部分。为了让学生掌握正确的计算方式,教师要引导学生在动脑思考、动手操作中深刻理解为什么这样算,以对算法的意义理解,让学生掌握分数运算的性质与规律,并结合前期所学知识,让学生结合已知推算未知,分析计算的方法,引领学生学以致用。结合案例实践,学生自然会思考“怎样算”“怎样好算”“为什么要这样算”等一系列问题,这就从简单的数学运算指向了算法掌握、算法优化与算理理解,助力学生数学思维完善发展。
理解“分数乘分数”的算理是基础,结合算理让学生进行具体问题的计算,是提高学生问题解决意识的有效方式。为了实现从算理理解到算法应用,教师结合各类问题让学生实践应用,鼓励学生积极尝试。
在课程的延伸总结阶段,教师进一步与学生一起回顾算理,展示一些直观可视的学习材料,让学生进行逻辑分析,深刻理解分数乘分数就是分子相乘做分子,分母相乘做分母,能约分的先约分。在学生对“分数乘分数”算理有所感悟后,教师再进一步延伸加法与乘法的对比算式,将分数运算运用在具体实践中,有助于学生今后的综合能力发展。
(作者单位:福建省漳州市龙海区浮宫镇下威小学)
编辑:张俐丽
