阚常兰 白孝波：基于问题导学的小学数学大单元教学

阚常兰 白孝波

一、教材分析

“多边形的面积”选自人教版小学数学五年级上册，本单元意在让学生以长方形的面积为基础，探索出梯形、平行四边形以及三角形的面积计算方法。

“多边形的面积”这一内容是小学阶段“图形与几何”领域学习的重要板块，几何图形的测量与计算是学生数学学习中不可或缺的重要能力，因此本单元内容在数学教学中的重要性可见一斑。所以本单元的教学重心不在于让学生机械地掌握图形面积计算公式，而是要让学生明确切割、填补等圆形转换思维，进而为今后的平面图形学习奠定基础。

二、课标要求

《义务教育数学课程标准（2022年版）》中在“课程内容”的“第二学段”中提出“要求学生探索并掌握三角形、平行四边形以及梯形的面积。”在实施建议中要求“学生能够在生活中感悟数学，用数学眼光发现问题，用数学思维思考问题，用数学方法解决问题。”

三、学情分析

五年级学生早在三年级下册数学教材中接触了“面积”这一内容，也掌握了“长方形、正方形面积的计算。有了三年级的学习基础，开展本单元的教学内容相对来说难度不大。

四、设计理念

本单元主要是探索多边形的面积，因此设置为三大教学板块，分别是基础探索板块——掌握平行四边形的面积；举一反三板块——三角形、梯形的面积；深化运用板块——简单组合图形以及实际问题应用。问题导学是本次单元教学设计的主要依据，意在以“指向明确、层层递进、贴近生活、有效引导”的原则设计教学问题，引领学生思维，让学生在主动思考的过程中落实单元学习目标。

五、教学目标

1.通过观察实践以及自主操作掌握三角形、平行四边形以及梯形的面积计算，并且能够计算出简单的组合图形面积，在生活中解决简单的应用问题。

2.借助方格纸探究、折纸观察等诸多实践方法，培养自主探究能力和图形观察能力，提高比较、推理能力，进而渗透转化意识和空间思维。

3.在解决实际问题和积极探索过程中，提高数学学习的成就感，感受数学与实际生活的联系，体会数学的魅力与趣味。

4.借助小组合作和自我思考的相互融合，培养独立思考和合作共赢的正确意识，感受数学探索中竞赛和合作的价值，进而树立正确的研讨学习意识。

六、教学重点

在实践探索中掌握三角形、平行四边形以及梯形的面积计算方法，并且能够计算出简单的组合图形面积，在实际生活中解决简单的应用问题。

七、教学难点

在自主探索中掌握正确的图形转化方法。

八、教学过程

●基础探索板块——掌握平行四边形的面积

（一）一个游戏问题——比比我们谁大？

教师出示组合图形的图案（图1、图2）。

随后出示一个思考性问题“这两个图案你觉得谁更大呢？能说说你的理由吗？”让学生从组合图形入手，思考几何图形的面积计算方法，随后初步学会观察图形。

教学预设：

答案1：直观上看，可能部分学生会觉得图2更大。

答案2：仔细观察过后，部分学生可能会发现这两个图案的边缘可以拼接，而且恰恰又可以组合为一个正方形，所以浅色部分的面积一样大。同理可推出深色部分的面积也一样大，因此这两个图形实际上面积是一样大的。

（设计意图：借助组合图形的大小问题引导学生思考其面积计算，并且在这一探究过程中将图案的转换拼接思维渗透其中，让学生初步建立起图形转化意识，在自主思考中强化数学思维。）

（二）一个问题回顾——谁还记得面积？

本环节教师可以直接引入“几何图形的面积”，即“刚才我们比大小，比的是这两个图形的什么呢？”“我们曾经学过面积吗？在几年級接触过呢？谁还记得计算方法和探究过程呢？”让学生在回忆长方形面积计算的基础上为多边形面积的计算奠定基础。

（设计意图：借助多个问题群直接指向三年级的面积学习，既能检验学生的基础学情，又能让学生回顾相应知识，降低本节课的难度，在思维方法和推理过程中提供直接引导，唤醒学生的几何学习思路。）

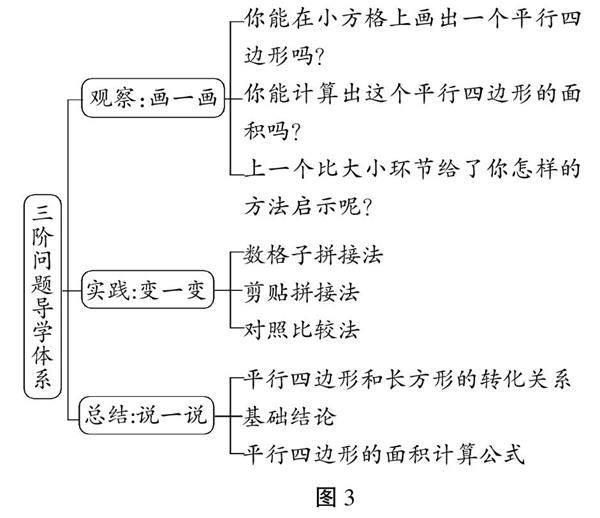
（三）一套问题体系——谁能发现联系？

教师设置层层深入的问题体系，引导学生主动提出数学猜想，进而在实践中多元验证，主动探索。

三阶问题导学思维导图预设（图3）：

教学预设：

方法一：数格子拼接法

学生基于三年级推导长方形面积计算公式的基础，借助小方格绘画并且在数格子计算面积的过程中，发现平行四边形的几个半格可以相互拼接变成一个长方形，进而将平行四边形的底和高与长方形的长和宽建立关系。

方法二：剪贴拼接法

有的学生愿意采用直观的剪接法，将平行四边形不规则的部分剪下后，结合图形拼接的转换思维，因此很容易就可以将这两部分进行拼接，最终共同构成一个长方形。

方法三：对照比较法

教师可以让学生对照观察，将画出的平行四边形和长方形进行叠加观察，再画出相应的面积阴影，自然也就明确了平行四边形和长方形的面积关系。

（设计意图：从基础到探究，从观察到实践，为学生的自主探索提供支架式引导，既能降低学生的学习难度，又能发挥教师的引领作用，保障学生的课堂主体地位。）

●举一反三板块——三角形、梯形的面积

（四）一个问题情境——谁来帮帮我们？

本环节教师为学生创设“几何图形的自白”这一问题情境（见图4），引导学生思考三角形和梯形的面积应该如何转化并推算。

（设计意图：生动有趣的问题情境能最大限度地让学生深入探究活动，在上节课的基础上进一步深入，将目光定位到三角形与梯形的面积公式推导，明确本节课的教学目标。）

（五）一张问题清单——問题梳理思路，总结面积计算

为了进一步让学生明确二者的面积计算公式，教师可以设计一张清晰的问题清单，让学生在完成清单的同时获得一定的知识引导，进而建立清晰的数学逻辑和图形思维。

问题清单：

△三角形的面积

1.采用拼接剪贴法时，三角形有几种剪法呢？（提示：上下剪开、左右剪开）

2.将三角形填补成长方形后，三角形的高和底和长方形的宽分别有什么关系呢？长方形的面积公式是长乘宽，所以三角形的面积公式应该是什么？观察二者的面积大小，千万不能忘记什么？

△梯形的面积

1.梯形变成长方形有几种方法呢？（提示：两角剪开拼接、拼接另一个一样大的梯形）

2.将三角形填补成长方形后，梯形的上底和下底和长方形的长有什么关系？所以梯形的面积计算公式应该是什么？

（设计意图：借助任务清单让学生完成自主探究，进而推导出三角形和梯形的面积公式，学会图形转化这一重要思想，为下一环节计算组合图形面积提供理论支撑。）

●深化运用板块——简单组合图形以及实际问题应用

（六）一个实际问题——她该怎么解决？

教师为学生出示一个实际问题，让学生运用所学知识，以小组合作的方式加以讨论，思考解决方法，最后开展“数学研讨会”，展示自己小组的解题思路以及最终结果。

实际问题：学校要举办班级布置大赛，班级中的小欣利用剪纸剪出了一个“A”的形状，但是她害怕剩下的剪纸不够了，你能计算出图形面积帮帮她吗？

小欣用一张红色不干胶纸剪了一个大写字母“A”，它的面积是多少？

（设计意图：借助学生熟悉的生活环境将实际问题蕴含其中，引发学生的思考，在小组讨论中强化学生的图形转化思维，检验学生的学习成果，夯实本单元的数学知识。）

（七）一张评价量表——问题引导评价，强化激励教育

教师为学生出示一张评价量表，让学生根据刚才的“数学研讨会”对各组加以评价。学生根据教师给出的评价标准切实给分，评选出本环节的“最佳小组”，最后由教师综合性评价。

量化评价表预设（见表1）：

（设计意图：转变学生主体地位，让学生同时成为评价者和被评价者，采用多元化的评价方式，借助量化表格实现过程性评价，借教师综合点评落实结果性评价。）

九、作业设计

课后在家中积极发现简单组合图形，并根据实际测量以及所学知识计算其面积。

十、教学反思

本次教学实施成果显著，基本实现了本单元的教学目标。学生掌握了三角形、平行四边形、梯形以及简单组合图形的面积计算方法。有效的问题导学让学生在自主探究和协作活动中发挥了主动性，降低了学习难度。因此，问题导学的创设让很多学生积极参与课堂，再次树立起了数学学习的自信心，有效规避了因大单元教学的综合性而让学生手足无措的教学弊端。

在对学生进行综合性评价的时候，因为我没有及时维护秩序，影响了部分学生的讨论效率，导致评价时间较短，没能对每组都提出建议，这是我今后要改正和努力的方向。

（作者单位：日照市北经济开发区莲海学校）

编辑：曾彦慧