善于建立数学模型，提升数学建模素养

◎ 海南省陵水黎族自治县陵水中学 赵李三

高中学生学过的函数、数列、不等式、解三角形等内容与实际问题有着密切联系，建立数学模型能有效解决与此相关的实际问题。在实际的问题情境中，教师要引导学生从数学的视角发现问题、提出问题、分析问题、建立模型、确定参数、计算求解、检验结果、改进建模，最终解决实际问题。下面结合笔者自身的教学实践，谈谈如何建立函数、数列、不等式、解三角形模型，发展提升数学建模素养。

一、建立函数模型，提升学生数学建模素养

1.根据已知数据，建立函数模型，解决实际问题，提升学生数学建模素养

函数应用的教学，要充分发挥好教科书的例题与习题作用，让学生参与函数建模，尤其是已知数据的问题，要引导学生对已知数据进行分析，抓住数量关系与等量关系，注意常量、变量，注意问题中量与量之间变化的基本特征及变化规律，恰当选择所学的函数模型来表达，建立函数模型，活用函数知识解题，提升学生数学建模素养。

问题1：某桶装水店，进价是10元两桶水，每天工作人员工资等固定成本是200元，经营情况如下表1。此店每桶水定价多少元时才能获得最大利润？

表1 某桶装水店经营情况

学生建模：根据以上表格已知数据发现什么问题，要求获利最大值，应用哪些知识，需要知道哪些量，注意成本有哪些量，注意数量关系：总价、单价、数量之间的关系；特别是从表中发现问题：单价的变化与销售量的变化存在着一定的规律，抓住数据中的单价变化引起销售量的减少。注意到减少量特征：销售单价每增加1元，日均销售量就减少40桶，明确解题思路，列出函数解析式，体会建模的过程，知道解题关键所在，化实际问题为函数问题，写出二次函数解析式进行计算，说明问题。建模：设在进价基础上增加x元后，日销售利润为y元，依题意得y=(520-40x)x-200=-40x2+520x-200，0＜x＜13,当x=6.5时，y有最大值，销售单价定为11.5元，可获得最大的利润。

学生参与了根据已知数据建立函数模型的过程，活用函数知识解题，提升学生数学建模素养。

问题2：假设你有一笔资金用于投资，现有三种投资方案供你选择,方案一：每天回报40元；方案二：第一天回报10元，以后每天比前一天多回报10元；方案三：第一天回报0.4元，以后每天的回报比前一天翻一番。请问你会选择哪一种投资方案？

学生建模：先建立三种投资方案所对应的函数模型，再通过比较它们的增长情况，选择投资方案。设第x(x∈N*)天所得回报是y元，方案一：y=40；方案二：y=10x；方案三：y=0.4×2x-1,对三种方案进行描述，要对三个模型的增长情况进行分析，得出投资1 ～6天，应选择方案一；投资7天，应选择方案一或方案二；投资8 ～10天，应选择方案二；投资11天（含11天）以上，应选择方案三。学生体会不同函数增长模型，增长变化存在很大差异。

2.收集数据，建立函数模型，解决实际问题，提升学生数学建模素养

生活中有一些实际问题需要留心观察、收集数据，发现和提出问题。在没有现成数据可用的时候，适当让学生观察现实情景问题，先收集并处理数据，对数据加以分析，根据已得到的数据转化为数学中的实数对点并按描点法画出散点图，结合散点图特征，直观地分析数据中各组实数对点的变化规律，恰当选择函数类型建立模型，求解得函数模型，最后解决问题。学生收集数据，建立函数模型，有效地提升学生的数学建模素养。

问题3：某学习小组同学为了解某沿海地区中学男生的身高（cm）与体重（平均值kg）情况，但没有现成数据，该小组的同学经过同有关单位人员了解，收集数据如表2。

表2 某沿海地区中学男生身高与体重情况

由表2能否发现某中学男生的身高与体重（平均值）有着一定的规律？能否建立恰当的函数模型说明此地区中学男生平均体重与身高度的函数关系？能否预测该地区身高175cm的中学男生的体重？

学生建模：以身高为横坐标，体重为纵坐标建立直角坐标系，以表中数据的实数对点描点画出散点图，由散点图恰当选择y=abx+c来刻画某沿海地区中学男生的体重与身高关系的函数模型。学生取三组数据（100，15）（120,20）（160,47.2）分别代入y=abx+c，算得a，b，c近似求得函数为y=2×1.02x，学生把表中已知数据代入函数解析式或作函数图像发现，这个函数模型能近似说明此地区中学男生平均体重与身高度的函数关系。当身高为175cm，即x=175时，y=2×1.02175，得y≈63.9，可以预测该地区身高175cm的中学男生的体重为63.9kg。

问题4：某学习小组的同学为了研究气温对热饮销售的影响，但没有现成的数据可用，该小组的同学在A热饮店进行观察且经店主同意收集经营台账如表3。

表3 A 热饮店经营台账

由表3数据能否建立热饮杯数随气温变化的函数模型？能否为店主预测某天气温20°C卖出的热饮杯数？

学生建模：首先将收集到的数据进行分析，发现热饮杯数是气温的函数，但没有现成的函数模型，利用学习过的函数图像，采用描点方法来研究热饮杯数与气温这两个量的变化规律，以气温为横坐标，热饮食杯数为纵坐标建立直角坐标系，画出散点图，结合散点图，直观分析表3数据的变化规律，选择所学过的函数类型。从散点图中看出：气温与热饮杯数之间的关系是气温越高，卖出的热饮杯数越少，这些点大致在一条直线的附近，于是可以近似地选择一次函数来刻画热饮杯数与气温之间的变化规律，需要写出一次函数，利用一次函数求法，学生求得：y=-2.4x+147。然后再用多组数据代入检验模型，发现这个一次函数模型与实际数据基本吻合，这说明该函数比较好地反映热饮杯数随气温的变化规律。将x=20代入y=-2.4x+147，得出y=99，预测这天卖出的热饮99杯。

学生收集数据，参与建模活动，通过画出散点图，分析散点图，恰当选择所学的函数类型，并按该类型的函数解析式求法求得函数，建立函数模型，有效地提升学生数学建模素养。

二、建立数列模型，提升学生的数学建模素养

数列在实际生活中有很多应用，人们在贷款、储蓄、购房、购物等经济生活中就大量用到数列知识。等差数列与等比数列在日常生活中有着广泛的应用，为此，通过实际问题的例题与练习题引导学生分析、建立等差数列模型或等比数列模型，解决实际问题，提升学生的数学建模素养。

问题5（习题）：某家庭打算在2010年的年底花40万元购一套商品房，为此，计划从2004年初开始，每年年初存入一笔购房专用存款，使这笔款到2010年底连本带息共有40万元，如果每年的存款数额相同。依年利息2%并按复利计算，问每年应该存入多少钱？

学生建模：设每年应存入x万元，根据题意，得x(1+2%)7+x(1+2%)6+…+x(1+2%)=40，根据等比数列前n项和公式，得,解得x≈52750（元）。

学生探究发现购房问题中的数学：某居民家庭经济每月总收入3000元，现有存款6万元，但必须留2万元至3万元以备急用。预选买房方案：方案1，买商品房：一套面积为80m2的住宅，每平方米售价1500元。方案2，买二手房：一套面积为110m2的二手房，售价为14.2万元，要求首付4万元。让学生应用学过的数列知识来解决最佳选择方案。适当启发：建议这个居民采用方案1。学生通过解决此问题，体会等差数列知识的应用价值，同时让学生练习运用等比数列知识解决实际问题，体会等比数列知识的应用价值，提升学生的数学建模素养。

三、建立不等式模型，提升学生的数学建模素养

运用不等式知识解决一些简单的实际问题，让学生认识一元二次不等式在现实世界的广泛应用，体会不等式建模，感受数学的应用价值，提升学生的数学建模素养。

问题6：某校园内有一块长为800m,宽为600m的长方形地面，现要对该地进行绿化，规划四周种花卉中间种草坪，若要求草坪的面积不小于总面积的一半，求花卉带宽度的范围。

学生建模：设花卉带的宽度为xm，表示出草坪与总面积的不等关系：，转化为解一元二次不等式问题求解，注意实际问题中条件的限制,解得0＜x≤100。通过实际问题的建模活动，提升学生的数学建模素养。

四、建立解三角形模型，提升学生的数学建模素养

正弦定理与余弦定理在实际测量中有许多应用，如测量距离、高度、角度等问题，让学生解决解三角形实际问题，体会建立解三角形模型，运用正弦定理与余弦定理解题，提升数学建模素养。

问题7：如图1，A、B两点都在河的对岸（不可到达），设计一种测量A、B两点间距离的方法。

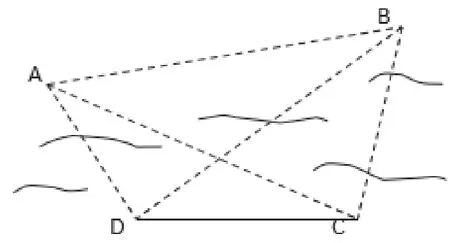
图1

学生建模：可以计算出河的这一岸的一点C到对岸两点的距离，测出∠BCA大小，借助余弦定理可以计算出A、B两点距离。测量者可以在河岸边选定两点C、D，测得CD=a，并且在C、D两点分别测得∠BCA=α，∠ACD=β,∠CDB=γ，∠BDA=δ。在△ADC和△BDC中，应用正弦定理得

计算出AC和BC后，再在△ABC中，应用余弦定理计算出AB两点间的距离：

总之，在高中数学教学中应注重让学生在建模中学会分析问题与解决问题，体会数学建模的过程与方法，应用数学知识解决实际问题，提升学生的数学建模素养。