基于MATLAB的结构振型模态分析
2024-05-27李建莉马君侯思晨
李建莉 马君 侯思晨
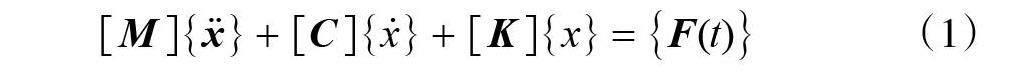

关键词: MATLAB 模态分析 有限元计算 频率响应分析
中图分类号: TH113.1 文献标识码: A 文章编号: 1672-3791(2024)01-0216-08
动力学分析的目的是分析在惯性、阻尼二者确定的条件下,结构或构件的动力学特性的变化情况。动力学特性分为以下几个方面:自振特性—频率和振型;不同的荷载效应对结构的位移、应力和应变会产生不同的效果; 周期和随机荷载的效应。静力学分析只能分析一个结构承受稳定荷载的情况,不足以全面分析所有的工况,尤其是那些稳定的荷载也包括很多动荷载的情况,而动力学分析就是在静力学分析的基础上,确定动力荷载的存在分析结构的位移,以及内力和振动频率随时间是如何变化的,从而达到实际最优化,为以后的设计和分析提供依据[1]。
模态分析是一种对结构动态性能进行研究的方法,通常用于工程振动领域。其中,模态系指的是结构的固有振动特征,每个模态系具有一定的自振频率,阻尼比及模态振型。对这些模态参数进行分析的方法叫作模态分析。亦可称为特征值分析,通过线性代数的原理求解代表模态特征向量和频率的特征值。根据其计算方式,可以将其划分为计算型和试验型两种。如采用有限元法进行了模态分析为计算型模态分析,对应各阶有特定的参数,即频率、阻尼、模态参数等。文章中主要介绍计算模态分析在振动领域的应用。在工程实际中为了进行简化计算,在进行模态分析时一般对振型进行线性假设。它的物理含义是:当多个激励共同作用于结构系统时,结构系统的响应就是这一组中各个激励分别起作用时的响应的线性累加。进行模态分析的意义是,每个物体都有它自身的固有频率,当外界激励作用在物体上时,同时接近这个频率会产生共振,从而导致物体的破坏。
1 模态分析基本理论
模态分析理论是研究和分析振动特性的一种技术手段,可以判断在各种工况下结构的振动特性[2]。通常针对一个线性定常系统进行动力学描述可以得到方程组:
式(1)中:[M] 为质量矩阵;[C]为阻尼矩阵;[K ]为刚度矩阵;{x(t)}为位移向量;{F(t)}为力矩阵。我们的目标是求解这个线性定常系统振动微分方程组得到{x(t)},也就是系统上各点随时间的位移。对于线性定常系统的振动微分方程组,通常采用的方法是将物理坐标转换成模态坐标,从而将方程组解耦,变成一组用模态坐标和模态参数来描述的独立方程,这样就可以得到系统的模态参数。其中变换矩阵为模态矩阵,每列为相应的模态振型。
每个集中质量的运动可用线性坐标来描述,描述模型中全部集中质量运动所需的最少独立坐标数目,称为系统的自由度数。这些独立坐标又被称为广义坐标,该坐标的数量与系统的自由度数目相等。
2 单自由度的弹簧振动
2.1 单自由度振动无阻尼系统建模与仿真
最简单的振动系统就是单自由度无阻尼(阻尼系数C=0)自由振动。弹簧振子是最简单的模型,如图1所示。以静平衡位置为原点建立独立坐标。对于单自由度的系统是方便求解的,对其进行动力学分析可以得到微分方程,如公式(2)所示,设劲度系数k=200,物块质量m=10,初始位移x=5。
通过公式进行进一步变化,可以看出在等式左侧x 的二阶微分就是代表加速度a,也就是说,加速度经过两次积分,得到位移。-k/m是系数,作为常数处理,在MATLAB 中利用Simulink 进行仿真,确定仿真基本思路。接下来建立Simulink 模型,主要用到积分模块,增益模块,初始值设为-20,仿真模型如图2 所示。启动仿真后,物块的加速度、速度、位移曲线显示在示波器中,结果如图3 所示。
根据图3 曲线图可以看出,对于单自由度振动方式,在不考虑阻尼的情况下,物块应在平衡位置来回振动,曲线围绕坐标轴上下波动,周期性进行变化,横坐标代表时间,纵坐标代表振幅,和预测情况是一致的。
4 有限元计算模态分析
事实上,每一个模态都有特定的固有频率、阻尼比和模态振型。它是机械结构的固有振动特性,只与结构的质量、刚度、约束状态有关,与外载荷无关,且每一阶固有频率与每一阶振型相对应[7]。如图8 所示,肩部关节为机械臂最关键的部件之一,模态为其主要影响因素,在MATLAB 中对其进行模态分析,主要分析机械臂的肩部关节连接部件在一定压力下可能的形变。机械臂通过多个关节链接,一端固定。这些链接结构强度要够大以避免电机带动负载运动时产生振动。机械臂终端的负载会让每个链接处产生压力。压力的方向取决于负载的方向。
本研究采用Inventor 对机械臂肩部关节进行建模,模态分析MATLAB 中有限元求解流程创建结构模型、导入几何形状、生成网格(见图9(a))、设置材料属性,弹性模量206 GPa、泊松比0.3、密度7.9 g/cm3,求解分析。利用facelabel 命令将面进行可视化出来,具体情况见图9(b)。方便设置边界约束和负载。通过加载F41 一端作为固定端,F8 一端作为自由端条件求解出固有频率,通过扩展模态获得关节的前六阶模态参数。
约束模态分析包含了很多种情况,由于结构的固有频率和振动模态在不同的约束状态下会发生变化,因此,施加约束后的模态分析可以反映结构的实际振动情况[7]。图10 为前六阶可视化模态振型。
通过模态振型图10 所示,可以发现一阶模态的固有频率值為317 Hz,一阶模态的振动方向沿Z 轴负向弯曲,变形主要在与相邻构件配合处;二阶模态固有频率值为431 Hz,振型体现为沿Z 轴的正方向垂直弯曲振动,同时沿Y 向存在拉伸变形,其形变产生在构件的边缘处,横向尺寸变小;三阶模态固有频率值为507 Hz,振型表现为挤压变形,其扭转振动峰值在自由端所在面的中心位置,并呈中部向边缘递减的状态,六阶模态固有频率值为798 Hz,主要变形表现为沿Z 轴垂直扭转变形,变形量最大值位置仍在振动峰值在自由端所在面的中心位置和边缘处,固定端约束值仍为0。
通过分析六阶次的频率及云图,模态振型大致经历了弯曲变形—拉伸变形—挤压变形—扭转变形,其中拉伸变形量最大为1.2 mm,最大变形出现的位置由边缘向中间,再向边缘的趋势。关节在此结构参数、材料下,变形不大,且在理论的可控范围内,可以有效地避免共振。本研究能为机械臂关节使用设计提供参考,极大地减少共振的发生,并为机械臂关节的优化设计和故障诊断提供参考依据。
5 频率响应分析
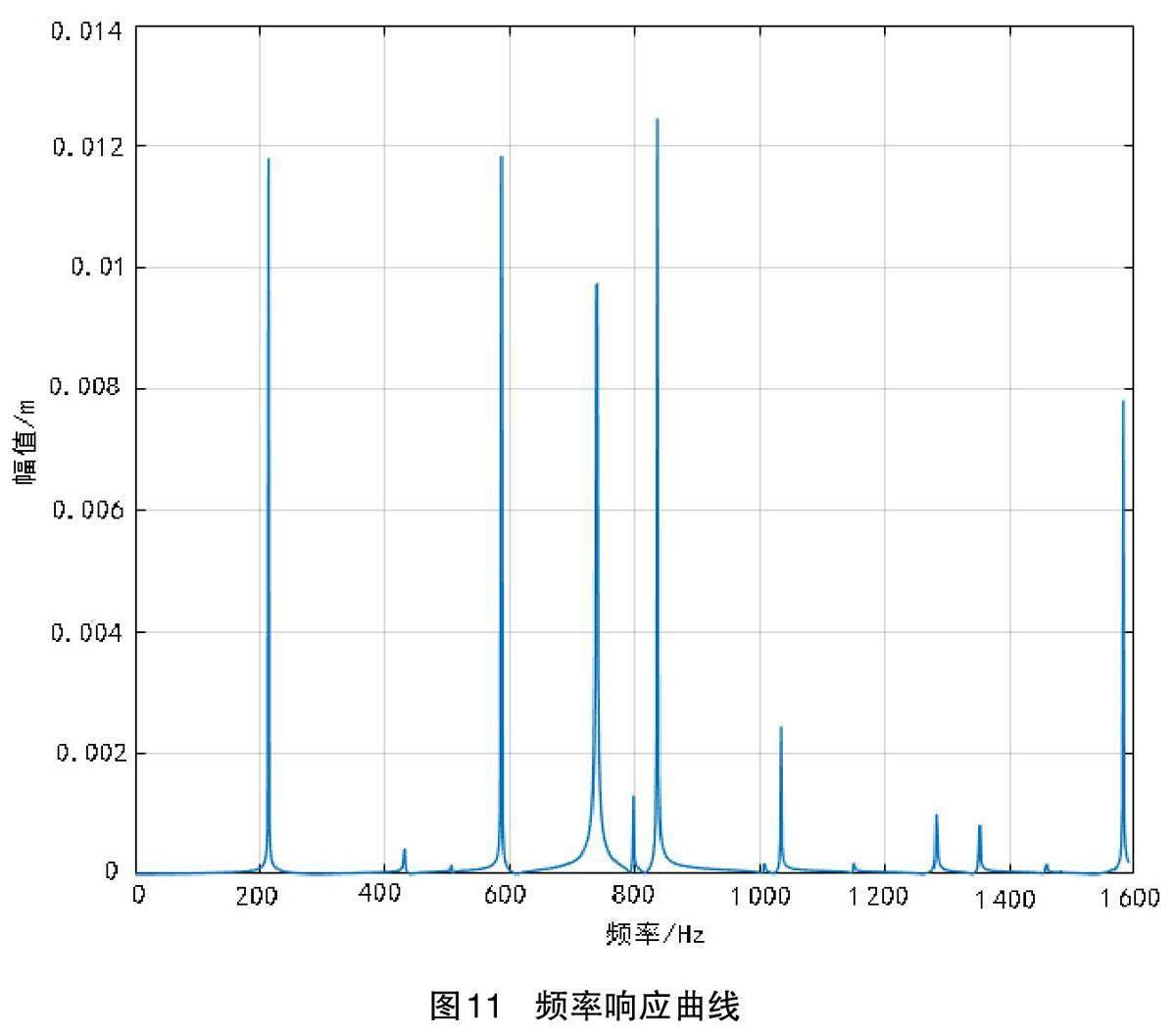
当结构在稳态下受到外界激励载荷时产生振动效应,可以通过频率响应分析方式,计算出给定外界激励载荷后结构在确定频率下的运动学参数,比如位移、速度、加速度,将运动学参数和频率绘制成曲线图,从曲线图中可以得到峰值响应,用于指导设计者预测产品的结构振动特性,验证设计是否可以消除疲劳、共振等有害效应的影响[8]。本文针对机械臂关节在压力载荷下频率响应分析。假设附加其上的连杆对各半面分别施加大小相等方向相反的压力,分析面上某点的频率响应和形变。同上述流程一样,创建结构,导入几何形状,生成网格。其他过程跟模态分析相同,区别在于加一个力,使用pressFcnFR 函数在面4 上施加边界载荷。这个函数作用一个推力和一个扭转压力信号。拉压分量是均匀的。扭力对左侧面施加正压力,对右侧施加负压力。
根据图11 的频率响应曲线可以发现,在频率为200 Hz、600 Hz、820 Hz 三处都出现了不同程度的极大值点,在这些频率下,很小的外界激励载荷便可以把系统激励振动起来,容易造成共振,所以此幅值的极大值点也称为共振峰,对应的频率称为共振频率,一旦关节发生共振,对机械臂的安全运行会产生较大影响。因此应避免关节发生共振破坏,影响系统的安全使用。通过计算发现关节整体振动微小,激发共振的可能性很小。在MATLAB 中也可以利用max 函数找到峰值响应频率对应的峰值和索引,可以看到所施加的载荷主要激发了部件的模态。
6 结语
本文利用MATLAB 中simulink 对单自由度弹簧振动运动学参数求解分析,利用脚本求解矩阵方程对多自由度的弹簧系统模态进行分析,进而基于有限元的思想对机械臂关节在压力载荷下模态分析和频响分析,得出进行模态研究一般思路和解决方案。为计算模态的场景利用在MATLAB 中内置函数做进一步探索研究提供了思路。
