股票市场系统性崩盘监测分析

李 燕，李 湛，郝晓玲

（1.怀化学院商学院，湖南怀化 418000；2.东莞理工学院经济与管理学院，广东东莞 523002；3.上海财经大学信息管理与工程学院，上海 200433）

0 引言

近年来，股票价格的急剧涨跌现象频繁发生，尤其是股票市场暴跌会给金融市场的稳定带来极大的挑战。股票市场崩盘会摧毁金融市场信心，造成投资者和社会的极大恐慌，从而使证券市场整体资源配置效率降低，而传统金融理论无法对股票市场崩盘做出有效解释，因此股票市场崩盘风险作为一种普遍存在且具有广泛影响力的风险因素进一步凸显。同时股票市场崩盘风险是市场参与者进行投资决策时重点关注的风险之一，当股票市场发生崩盘时，往往是多市场及多个股同时出现崩盘，投资者不能通过多元化的投资组合来分散投资风险，股市崩盘是一种极端的系统性风险。

对股市崩盘的研究主要聚焦在以下几个方面：一是研究股价崩盘的影响因素，主要影响因素包括公司治理[1,2]、公司社会责任[3,4]、股利政策[5]、公司信息质量[6,7]、制度与环境[8]、投资者偏好[9,10]等；二是对股票市场崩盘风险的度量，主要指标包括负收益偏态系数（NCSKEW）及股票收益上下波动的比率（DUVOL），这两个指标值越大，即上市公司股票收益率的偏态系数负的程度和左偏的程度越大，表明股价崩盘的风险也就越大。

目前，对股票市场崩盘的研究主要集中在对崩盘的影响因素及崩盘的风险度量方面，且从个股层面研究较多，对市场层面研究较少，但股票市场整体崩盘比个股崩盘危害性更大、影响更加深远。股票崩盘的时点检测对市场投资者进行投资决策及市场管理者进行市场风险管理具有十分重要的现实意义。本文的主要贡献在于：（1）历次股票市场崩盘看似是在“毫无征兆”的情况下发生的灾难性和突发性极端事件，但股票市场崩盘真的是毫无征兆吗？如果不是，那么在市场崩盘前，股票市场到底发生了什么变化？如何检测这些变化？对这三个问题进行深入研究，毫无疑问对认识股票市场崩盘及减轻崩盘的灾难性危害具有非常重要的理论及现实意义。（2）使用重构相空间的方法把一维股票价格时间序列嵌入高维相空间中，进而可以在一个拓扑性质不变的高维相空间中通过分析状态向量的轨迹来研究股票市场的动力学行为，通过研究崩盘前市场内生性结构变化来发现股票市场崩盘前的市场“异常”行为，为股票市场崩盘研究提供“观察”股票价格时间序列的新视角和新方法。

1 递归图及BG算法

Eckmann 等（1987）[11]构建的递归图方法选定恰当的延迟时间及嵌入维数，把一维混沌时间序列重构到一个高维相空间中，可以在高维相空间中分析状态轨迹的特征，进而研究混沌时间序列的非线性动力学特征。传统对时间序列进行分析的方法通常对序列的长度及平稳性有一定的前提假设，但递归图方法对时间序列的长度及平稳性没有严格的假设，因此该方法逐渐成为对短时非平稳时间序列进行分析的有效工具。对一维时间序列{xi|i=1，2，…，n}，可以使用相空间重构方法，通过选取相空间维度m和延迟时间τ，就可以把一维时间序列重构到一个m维的相空间，进而可以获得一个状态向量集，其中，i=1，2，…，n′，n′=n-(m-1)τ。向量集可以用来表示一维时间序列xi=(1，2，…，n)在高维相空间中的状态轨迹。利用递归图可以在二维图形中直观地分析高维相空间中系统状态轨迹的动力学行为特征，在递归图中主要包括以下几种几何结构：孤立点、对角斜线、垂直直线和水平直线。Eckmann等（1987）[11]通过对递归图中的这些几何结构的数量特征进行量化，构建了递归量化分析（RQA）方法。其中，层流性指标刻画了垂直结构中的递归点占所有递归点的比例，反映了复杂系统中出现层流状状态的概率，计算公式如下：

其中，P(v)表示递归图中线段长度的分布函数，v表示线段长度，minv表示最短线段长度，N表示时间序列长度，LAM值反映了复杂系统停留在某个状态的动力学特征，Marwan 等（2007）[12]指出该指标能够发现复杂系统在不同混沌状态之间的转变。

金融时间序列数据一般都为非线性、非平稳序列，当外部环境发生变化时，会导致金融时间序列发生结构突变并出现新的特征，对这些结构突变的认识有助于研究金融市场的演变规律。Bernaola-Galván 等（2001）[13]构建了一种启发式分割算法（BG 算法）来探测具有非线性及非平稳性特征的人类心率变化的均值变异点。该时间序列突变检测算法是基于滑动t检验的思想，把非平稳时间序列分割成多个具有不同均值的平稳子序列，所得各子序列表征不同的物理背景，有效解决了以往时间序列突变检测方法基于平稳及线性过程假设条件的问题。同时由于在分割时运用多次迭代的一分为二的算法，极大地减少了检测计算量，该方法不仅实用性较好，而且白噪声与尖峰噪声对异常点检测结果的影响较小。本文联合运用递归定量分析（RQA）方法及BG算法来对金融时间序列异常突变时点进行检测，提出了一种新的股市崩盘突变时点的探测思路。

2 实证分析

2.1 数据来源

本文从Wind 金融数据库收集了道琼斯工业平均指数1926 年1 月4 日至1936 年12 月31 日每日收盘价，共2351 个数据；1970 年1 月2 日至1978 年12 月29 日每日收盘价，共2273 个数据；1984 年1 月3 日至1991 年12 月31 日每日收盘价，共2022 个数据。还收集了纳斯达克指数1995 年1 月3 日至2004 年12 月31 日每日收盘价（由于互联网投机泡沫主要是中小科创型企业引起的，因此选择纳斯达克指数比道琼斯工业平均指数更恰当），共2519 个数据；以及澳大利亚等23 个国家（地区）2006 年1月1 日至2009 年12 月31 日澳洲AS30 等股票指数每日收盘价。

2.2 美国股票市场泡沫形成及市场崩盘过程分析

先分析影响全球的金融经济危机事件中股票市场崩盘过程。由于道琼斯工业平均指数历史悠久，其他股票市场在部分金融危机事件发生时并未成立，没有数据可供分析研究，因此本文选取美国道琼斯工业平均指数作为研究对象，分析金融危机发生时美国股票市场崩盘过程。对1929—1933 年经济大萧条、1973—1975 年由石油危机引发的经济危机、1987—1988 年“黑色星期一”金融危机、1999—2001 年的互联网投机泡沫危机这四次全球重大金融经济危机事件进行分析。使用递归量化分析中的LAM值来分析市场泡沫起始时间，实现对股市崩盘前内生性结构突变时点的检测。从下页图1 可以看出，股票市场在泡沫积累阶段，LAM值会出现轻微下跌。当市场趋于不稳定状态，临近崩盘阶段时，LAM值会出现急剧下跌，LAM值的这一变化过程在四次股票市场崩盘中都极为相似，而且LAM值的变化都非常明显，从时间点来看，市场内生性结构突变的时点都比市场崩盘时点提前较长一段时间。到市场崩盘的最后阶段，LAM值会继续出现急剧下跌或者下跌之后处于波动状态。经过一段时间的波动，当LAM值趋于新的稳定状态或者回到下跌前区域时，市场通常表现出止跌企稳现象，因此当市场临近崩盘时，市场的内生性结构会出现异常突变。在1929—1933 年经济危机前后，LAM值的变化体现出了美国股市所经历的完整的波动过程：泡沫形成（1918 年1 月左右开始形成泡沫，LAM值开始下跌）→崩盘临近（1929 年1 月临近崩盘，LAM值开始急速下跌）→崩盘（1929 年9 月开始崩盘，LAM值继续下跌，从崩盘临近到崩盘发生，LAM序列的结构提前8 个月出现突变）→企稳复苏（1933 年4 月股市开始止跌企稳，LAM值基本回复到下跌之前的水平）。1929—1933 年经济危机前，美国的工业生产指数在1921 年时平均仅为67（1923—1925 年为100），但到1928 年7 月时已上升到110，再到1929 年6 月时则上升到126。人们对美国股票市场行情非常乐观，美国时任财政部长安德鲁·梅隆也于1929 年9 月向公众保证：“现在没有担心的理由，这一繁荣的高潮将会继续下去。”但到1929 年10 月29 日，当天的股市暴跌。依据LAM值的监测结果，美国股市从1928 年1 月开始形成泡沫，在1929年1 月临近崩盘，1929 年9 月到达崩盘临界点。另外，2000 年左右发生在美国股票市场的互联网泡沫危机中，LAM值的变化也监测出了美国股市所经历的完整波动过程：泡沫形成（1997 年11 月左右开始形成泡沫，LAM值开始下跌）→崩盘临近（1999 年3 月临近崩盘，LAM值开始急速下跌）→崩盘（2000 年3 月开始崩盘，LAM值继续下跌，从崩盘临近到崩盘发生，LAM序列的结构提前11 个月出现突变）→企稳复苏（2004 年2 月股市开始企稳复苏，LAM值基本回复到下跌之前的水平）。因此历次股票市场崩盘貌似毫无征兆地发生，但在崩盘前市场的内生性结构已经发生了变化，这为认识股票市场崩盘提供了一个新的思路和视角。

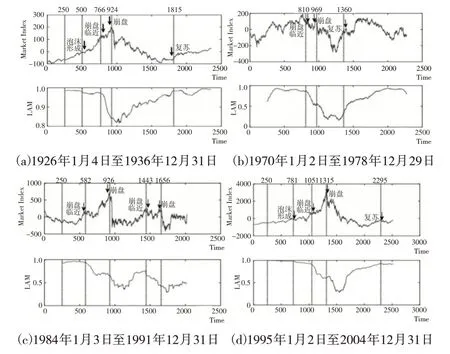
图1 市场崩盘过程中LAM 值的变化

2.3 美国股票市场崩盘前动力学结构突变时点检测

用LAM值检测股票市场崩盘前市场内生性结构的突变时点存在以下不足：市场结构突变时点只能通过直观观测获得，尚不能对市场内生性结构突变时点进行量化检测。股票市场是非线性复杂系统，具有多层次性及非平稳性特征，因此线性结构突变检测方法对股票市场崩盘前内生性结构异常突变时点检测并不适用。Bernaola-Galván等（2001）[13]构建的BG算法将非线性及非平稳时间序列分割成不同尺度下的平稳子序列，该算法对非线性及非平稳时间序列结构突变时点检测取得了较好效果。因此本文引入非线性时间序列突变检测的启发式分割算法来检测股票市场崩盘前市场内生性结构的突变时点，增强市场结构突变时点检测的科学性及可解释性。将递归量化分析（RQA）方法及BG 算法一同使用，对股票市场崩盘前市场内生性结构突变时点进行检测。

由图2 可以看出，在1929—1933 年经济大萧条期间，BG算法检测到道琼斯工业平均指数的LAM值在1928年9月11日、1929年4月3日、1929年5月17日出现相位异常突变，在此过程中伴随着LAM值的连续下降，市场泡沫从1928 年9 月11 日开始形成，1929 年4 月3 日、1929 年5月17日，市场在短时间内连续出现相位异常突变，市场不稳定状态加剧，市场进入临近崩盘状态，实际上市场在1929年10月出现雪崩式暴跌。在1973—1975年由石油危机引发的经济危机期间，BG 算法检测到道琼斯工业平均指数的LAM值在1973年6月13日、1974年1月6日、1974年3月29日及1974年7月1日出现相位异常突变，显示市场泡 沫从1973 年6 月13 日开始形成，1974 年1 月6 日、1974年3月29日及1974年7月1日，市场在短时间内连续出现相位异常突变，市场不稳定状态加剧，市场进入临近崩盘状态，实际上市场在1974年11月出现崩盘，之后市场出现连续下跌，到1974 年12 月道琼斯工业平均指数下跌50%。在1987—1988 年“黑色星期一”金融危机期间，BG算法检测到道琼斯工业平均指数的LAM值在1985 年6月3日、1985年10月2日、1986年9月12日及1986年10月16日出现相位异常突变，显示市场泡沫从1985年6月3日开始形成，市场在1985 年10 月2 日、1986 年9 月12 日及1986年10月16日短时间内连续出现相位异常突变，市场不稳定状态加剧，市场进入临近崩盘状态，实际上在1987年10 月19 日道琼斯工业平均指数骤跌508 点，下跌幅度为22%，这次暴跌震惊整个金融界，并在全球股票市场产生“多米诺骨牌”效应，世界上主要金融城市伦敦、法兰克福、东京、香港、新加坡等地股市均受到强烈冲击。在21世纪初互联网投机泡沫危机中，BG 算法检测到纳斯达克指数的LAM值在1999 年5 月19 日 及2000 年2 月14 日出现相位异常突变，显示市场进入临近崩盘状态，实际上美国纳斯达克指数在2000 年3 月13 日一开盘就出现暴跌，从5038 点跌到4879 点。在2000 年6 月5 日、2000年7 月25 日、2000 年9 月25 日，纳斯 达克指数的LAM值连续出现相位异常突变，实际上在2000 年3 月10 日NASDAQ 指数到达5048.62 的最高点，随后纳斯达克指数出现连续下跌。网络经济泡沫的崩溃发生在2000 年3 月到2002 年10 月间，互联网技术公司的市值蒸发了约5 万亿美元。美国股票市场指数的LAM序列和非线性时间序列突变检测的启发式分割算法（BG 算法）对检测崩盘前市场内生性结构异常突变时点非常有效，一般在市场崩盘前的3个月到8个月市场内生性结构会连续出现异常突变。

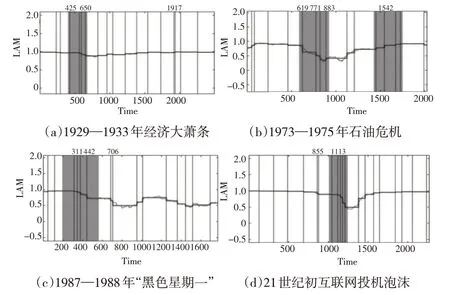
图2 金融危机期间美国股票市场LAM 序列的异常突变时点

2.4 2008年全球金融市场崩盘前市场内生性结构异常突变时点检测

使用递归量化分析方法及BG 算法对12 个发达国家（地区）（澳大利亚、奥地利、瑞士、新西兰、法国、德国、中国香港、日本、荷兰、新加坡、英国和美国）的金融市场和11个新兴国家（地区）（中国、阿根廷、巴西、埃及、印度、印度尼西亚、以色列、韩国、马来西亚、墨西哥、中国台湾）的金融市场的股票市场在2008年金融危机期间市场崩盘前市场内生性结构异常突变时点检测进行研究，结果如下页表1所示。

从表1可以看出，在2007年7月到2007年10月之间，绝大多数股票连续出现内生性结构突变，2007 年12 月以后全球股票开始出现崩盘。这说明股票市场崩盘貌似是在“毫无征兆”的情况下发生，但实际上股票市场在崩盘前系统相位会发生连续异常突变，股票市场崩盘实际上也是“有迹可循”。本文所构建的股票市场崩盘的内生性结构异常突变时点检测方法，通过使用重构相空间的方法把一维股票价格时间序列嵌入高维相空间中，进而可以在一个拓扑性质不变的高维相空间中通过分析状态向量的轨迹来研究股票市场的动力学行为，通过研究崩盘前市场内生性结构变化来发现股票市场崩盘前的市场“异常”行为，为股票市场崩盘研究提供了新视角和新方法。

3 结论

本文将RQA方法和BG算法相结合，对主要金融或经济危机中股票市场崩盘过程进行分析，得到如下结论：

（1）使用递归图及递归量化方法能够检测到被视为股票市场内生性结构相变的市场内生崩溃之前的临界状态。对1929—1933 年经济大萧条、1973—1975 年由石油危机引发的经济危机、1987—1988 年“黑色星期一”金融危机、1999—2001 年的互联网投机泡沫这四次全球重大金融经济危机事件进行分析。研究发现，股票市场在泡沫积累阶段，LAM值会出现轻微下跌。当市场趋于不稳定状态，临近崩盘阶段时，LAM值会出现急剧下跌现象，LAM值的这一变化过程在四次股票市场崩盘中都极为相似，LAM值的变化都非常明显，且从时间点来看，市场内生性结构突变的时点都比市场崩盘时点提前较长一段时间。因此历次股票市场崩盘貌似毫无征兆地发生，但在市场崩盘前市场的内生性结构已经发生了变化。

（2）对金融危机期间美国股票市场LAM序列的递归图进行分析发现，四次金融危机期间美国股票市场的LAM序列均呈现类分形自相似性结构，序列呈现复杂性特征。在递归图中均有空白带存在，说明LAM序列存在相变，在这些相变点处产生了LAM序列的异常突变。市场指数的LAM序列和非线性时间序列突变检测的启发式分割算法（BG算法）对检测崩盘前市场内生性结构异常突变时点非常有效，一般在市场崩盘前的2个月到8个月，市场内生性结构会连续出现异常突变。

（3）通过对2008 年金融危机前后12 个发达国家（地区）和11个新兴国家（地区）的股票市场进行分析发现，各国家（地区）股票市场的LAM值在2007年7月到12月期间均连续出现异常突变，2007年底到2008年底各国家（地区）股票市场均出现崩盘，在市场崩盘前的3～12 个月内，各国家（地区）股票市场的内生性结构均出现连续异常突变。