适用于无人水下潜航器电池管理系统的SOC-SOH 联合估计

卢地华，周胜增，陈自强

(1.上海船舶电子设备研究所，上海 201108；2.水声对抗技术重点实验室，上海 201108；3.上海交通大学 海洋工程国家重点实验室，高新船舶与深海开发装备协同创新中心，上海 200240)

水下作业环境一直以来都是各国关注的重点，近年来国内外对无人水下潜航器（unmanned underwater vehicle，UUV）技术进行了广泛研究与应用[1].UUV 作为典型的水下作业工具，可以完成水下情报监视、侦察、反潜、探测、识别、海洋调查、通信及载荷输送等不同的作业任务[2].目前研制的UUV 大多是以电池动力为主，综合考虑成本、放电稳定性、可维护性及安全性，应用锂电池尤为典型[3-4].UUV 因作业时间受能量制约，适合选用高能量密度电池作为动力源（如常用的三元锂离子电池），无人系统对状态反馈的精度要求高，其中荷电状态（state of charge，SOC）精度易受其他状态的衰减干扰，因此对系统进行状态联合估计必不可少.

UUV 精确的电池SOC 估计可以提高能量利用率和设备续航时间敏感性[5].工程上常用安时积分法进行SOC 粗略估计，不仅依赖传感器和初状态精度，还存在累积误差[6].基于模型的估计方法应用较多，能以较高精度描述特征，所需的数据量较少[7-8]；鉴于模型内部的非线性关系，应用扩展卡尔曼滤波（extended Kalman filter，EKF）进行SOC 估计具有较高精度[9-11].随着充放电的进行，电池老化使得容量和电压关系发生变化.若不修正，则设备将得到错误反馈.电池健康状态（state of health，SOH）很好地描述了老化程度，且和SOC 之间存在耦合关系，可以利用SOH 修正SOC 估计精度.SOH 反馈主要依赖测试直接获取或模型间接获取，前者须基于实验室环境，因UUV不方便经常拆卸，在实际工程应用中受限；后者可以通过外特性数据来实时估算，具有较高的可实施性，常用方法有差分电压分析[12]、容量增量分析[13]、充电数据分析[14]等，结合高斯过程回归[15]、神经网络[16]算法进行估计，但根据设备实际作业工况选取表征十分重要.王志福等[17]提出深度置信网络和自适应EKF/H∞滤波融合算法在卷积神经网络模型下的SOC-SOH 联合估计，该方法具有较好的精度和鲁棒性，但算法融合使计算复杂度增加，实际工程应用依赖硬件支撑，且多模块应用对UUV 电池舱存在挑战.赵靖英等[6]提出基于模型和分数阶理论的SOC-SOH 联合估计，在低频计算中能以少参数和高精度进行估计，但十分依赖模型精度，且对UUV 内部成组使用的电池系统来说，不一致性可能带来较大的估计误差.

为了解决估计误差及工程实现的问题，提高设备状态反馈的精确性，本文提出适用于UUV 电池系统的SOC-SOH 联合估计方法.采用遗忘因子递推最小二乘算法（forgetting factor recursive least squares，FF-RLS）在线辨识模型参数，结合EKF 算法进行SOC 估计.通过多维表征结合改进支持向量回归（support vector regression，SVR）进行SOH 估计；利用状态间耦合关系联合修正估计，提高状态反馈精度，通过实验验证方法的有效性.

1 电池实验设计及模型建立

1.1 电池实验

三元电池具有高能量密度和较高的充电效率，非常适用于UUV 对尺寸结构的要求，在UUV中应用较多.其中国外部分UUV 应用锂电池的情况如表1 所示[4].

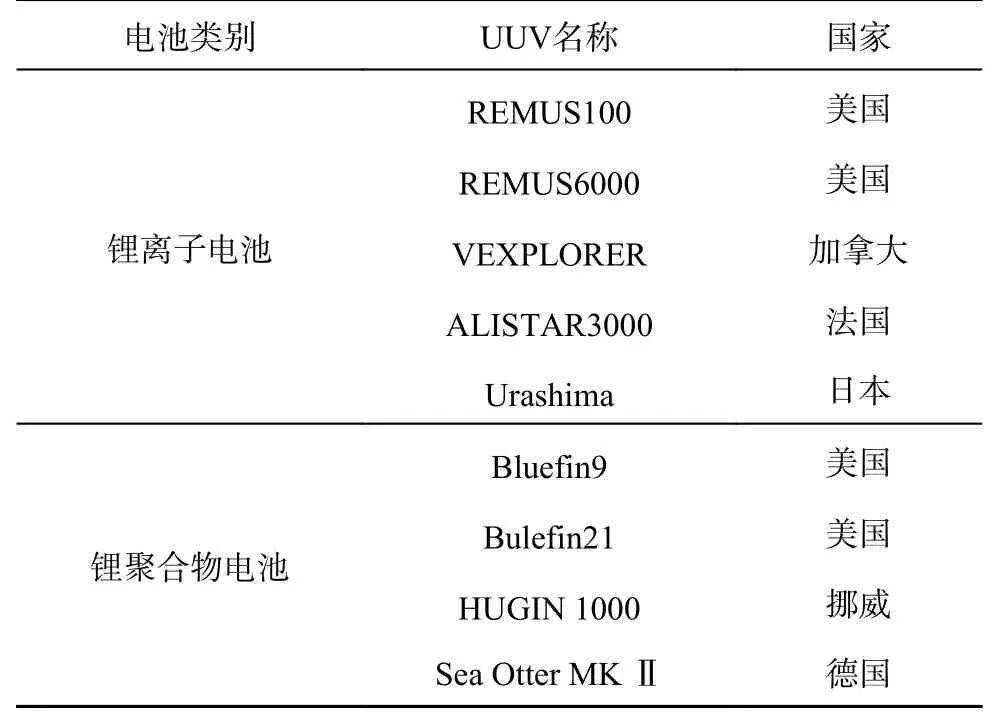
表1 UUV 应用锂离子电池的情况Tab.1 Application of lithium-ion batteries in UUV

将额定容量为10 A·h 的三元镍钴锰酸锂电池分为4 组进行实验，获取不同老化状态下的各项参数，记录循环的充放电数据，包括电流、电压、容量等数据.开展特性测试，包括开路电压（open circuit voltage,OCV）、混合功率脉冲特性(hybrid pulse power characteristic,HPPC)、动态应力测试(dynamic stress test,DST)和美国联邦城市运行工况(federal urban driving schedule,FUDS)；搭建台架，以获取不同老化状态下的电池数据，如图1 所示.

图1 电池充放电测试台架Fig.1 Test bench for battery charging and discharging cycles

将采集步长设置为0.1 s，对4 组电池均进行全寿命周期下的老化试验，获取电池全寿命周期下的外特性数据.

1.2 电池建模

等效电路模型（equivalent-circuit model，ECM）可以使用简单元件模拟电池输出特性，适用于对外特性的研究.一般ECM 中串联RC 网络越多，模型精度越高，但建模所需的参数增加，计算复杂度越高.为了较好地满足电池电化学极化、浓差极化不同时间常数的极化过程，建立二阶ECM，如图2 所示.

图2 二阶等效电路模型Fig.2 Second-order equivalent circuit model

图中，Uoc为开路电压，Ut为端电压，U1、U2为2 个极化电压，Rs为欧姆内阻，IB为干路电流，R1、R2为2 个极化内阻，C1、C2为2 个极化电容.由基尔霍夫电压定律，易得

通过OCV 测试获取当前状态下的SOC-OCV关系，采用7 阶多项式拟合，结果如图3 所示.

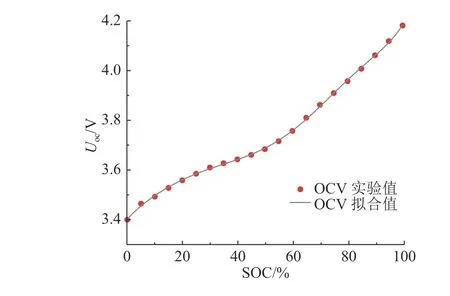
图3 电池SOC-OCV 拟合曲线Fig.3 SOC-OCV fitting curve of battery

建立相关状态空间方程的离散形式如下：

式中：k 为离散点，Δt 为采样间隔，Cn为电池容量.

1.3 参数辨识

结合采集的电池数据，采用RLS 进行参数辨识.将ECM 转化为ARMA 模型，将式（2）经过拉普拉斯变换为

模型的传递函数为

令τi=RiCi（i=1,2），Et(s)=Uoc(s)-Ut(s)，由双线性变换原理，可得z 平面离散传递函数为

式中：α1、α2、β0、β1、β2为待定系数.离散方程为

令

则式（8）可以转化为FF-RLS 可辨别的形式：

模型参数方程组为

解耦方程组，可得Rs、R1、R2、C1、C2.

2 状态表征因子及SOH 估计模型

2.1 状态表征因子的提取

SOH 反映了电池老化程度，是缓变量.为了探究老化过程中与SOH 相关度高的外在表征，开展深度老化实验.鉴于电池实际工作过程中放电工况无法预知，但充电工况相对平稳固定，且单个循环内可以认为SOH 基本不变，因此可以通过实验结果及理论分析从充电工况数据中提取与老化相关的表征.

2.1.1 恒流阶段表征 随着老化的加剧，电池内阻增大，恒电流在相同时间内充入容量相等，但电压变化增大.分析不同老化程度下的充电数据，结果如图4 所示.图中，U 为电压.

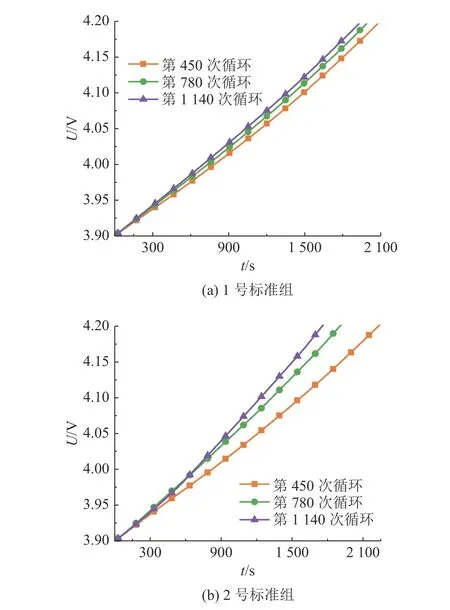
图4 恒流充电阶段的电压变化曲线Fig.4 Voltage curve during constant current charging stage

由实验结果可知，随着充放电循环的进行，相同充电时间内的电压变化幅度增大，意味着充电使电池变化同电压差的时间逐渐减少，充电时间和电池容量存在正相关性.考虑到实际工程应用中初始充电电压的不确定性，应选择较大的起始电压到恒流截止电压的充电时间为第1 个表征因子(H1).

2.1.2 恒压阶段表征 随着电池老化的加剧，电池恒压充电时间逐渐增加[18].分析不同老化程度下的电池恒压阶段充电数据，结果如图5 所示.图中，I 为充电电流.

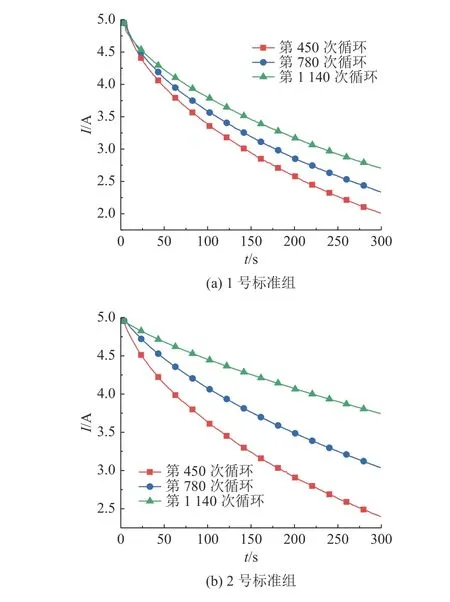
图5 恒压充电阶段的电流变化曲线Fig.5 Current curve during constant voltage charging stage

由实验结果可知，由于充电截止电流相同，充电时间增加意味着老化后期的电池在恒压阶段的充电电流下降速率减缓，相同时间内电流均值和电池容量存在负相关性.考虑到实际工程应用中可能出现的充电周期不完整性，选取恒压充电开始后一小段时间内的电流平均值作为第2 个表征因子(H2).

2.1.3 容量增量的表征 随着电池老化的加剧，容量和电压关系会发生变化，分析电池容量增量（incremental capacity,IC）是可行的方法[19].分析电池不同老化程度下的IC 与电压的对应关系，结果如图6 所示.图中，Q 为充电过程中的电池容量.

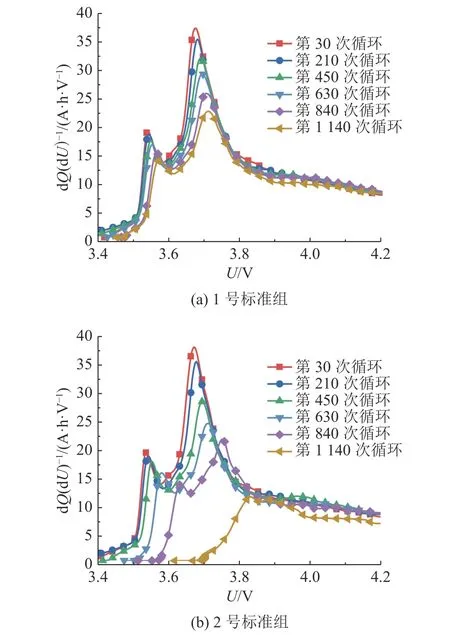
图6 容量增量随电压的变化曲线Fig.6 Incremental capacity curve with voltage variation

由实验结果可知，IC 曲线具有独特的形状、高度和位置，它反映了电池充放电过程中的电化学反应.其中存在2 个明显的高峰，表示当前电压下电池容量随电压变化的斜率，有研究表明峰值的变化可能与电池的活性材料损失有关.随着老化的加剧，两峰高度逐渐降低，对应的电压位置逐渐增大，因此可以从以上变化趋势中提取相关表征[20].由于两峰有明显的跟随性质，为了避免多重共线性影响，考虑提取第2 峰的高度、位置作为第3、4 个表征因子（H3、H4）.

2.2 SOH 估计建模

为了验证表征因子的合理性，对因子进行相关性分析.结合标准组1#电池的测试结果，对比如表2 所示.

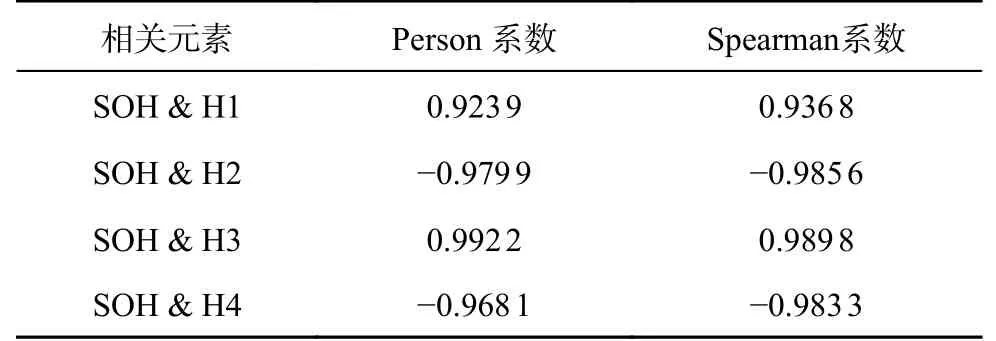
表2 表征因子与SOH 的相关性Tab.2 Correlation between characterization factors and SOH

由实验电池表征因子与电池SOH 的相关性可知，本文所提的因子可以对电池SOH 进行表征.考虑到所提的因子和相关性验证都是基于本文实验电池的数据，无法说明方法具备普适性.为了验证表征因子的泛用型，联立美国国家航空航天局卓越预测中心（National Aeronautics and Space Administration，NASA）公开数据集中的2 A·h 的18650 型电池进行验证，结果如图7 所示.

图7 表征因子与SOH 的相关性Fig.7 Correlation between characterization factors and SOH

以上分析可知，所提表征与电池容量间具有良好的相关性，基于笔者[21]先前的研究，联立前文所提的4 种因子，建立基于四维输入的SVR 模型.采用粒子群优化算法（particle swarm optimization,PSO）自适应确定参数，选取2 个实验标准组数据进行SOH 估计，具体流程如下.1）结合采集的电池数据，选取当前循环状态下的四维因子（H1、H2、H3、H4）.2）将四维因子作为输入，实时通过PSO 优化SVR 模型参数.3）输出当前循环下的SOH 估计结果.估计结果如图8 所示.

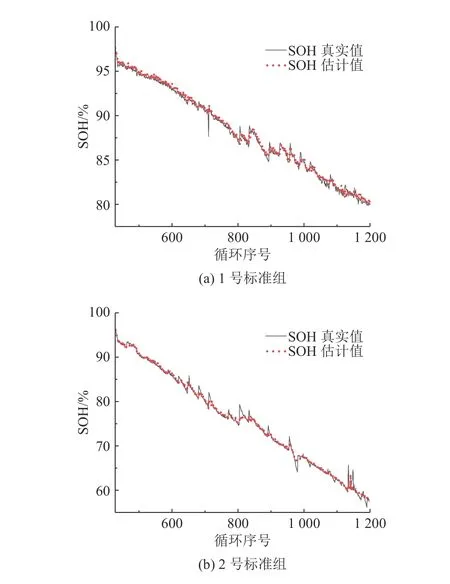
图8 标准组电池的SOH 估计结果Fig.8 SOH estimation results of standard group batteries

对以上2 组电池结果进行估计精度计算，均方根误差（RMSE）分别为0.003 9、0.006 8，平均绝对百分比误差（MAPE）分别为0.351%、0.6108%，可以证明所建立的SOH 估计模型具有较好的效果.

2.3 SOC 估计建模

SOC 估计可按以下流程开展.

1）参数初始化，设置初始协方差矩阵P0、初始状态x(0)、初始模型参数.

2）引入遗忘因子进行参数迭代更新.

3）结合更新的模型参数，进行状态初步预测：

4）预测协方差矩阵P(k)：

式中：Q 为噪声矩阵.

5）更新卡尔曼增益K(k)，其中C(k)为输出矩阵：

式中：r(k)为测量噪声.

6）状态更新：

式中：e(k)为电压估计值与测量值的误差.

7）更新协方差矩阵：

式中：E 为单位矩阵.

8）令 k=k+1，进入下一次循环.

3 状态联合估计

3.1 SOH-SOC 耦合关系的探究

随着电池老化的加剧，SOH 不断降低，电池最大可用容量不断减小，这会使SOC 估计的误差逐渐增大.通过充放电老化试验数据，探究SOCOCV[22]在不同SOH 下对应关系的改变，选取电池初始循环、第210 次循环、第450 次循环、第630 次循环、第810 次循环以及第1 000 次循环数据进行分析，结果如图9 所示.

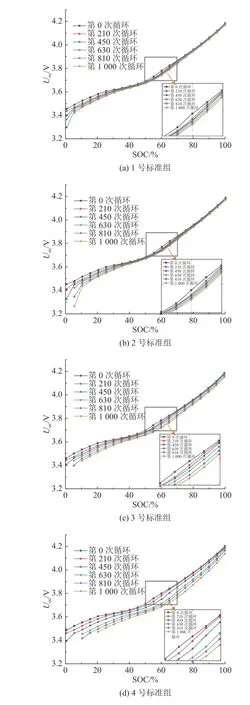
图9 不同老化程度下的SOC-OCV 对应结果Fig.9 SOC-OCV curves at different aging stages

从结果可以看出，随着循环数的增加，SOCOCV 曲线特征明显改变.为了提高电池的估计精度，对不同SOH 下的SOC 估计进行修正.

3.2 联合估计流程

随着充放电循环的不断进行，电池容量将会出现衰减，这会导致在不同老化状态下的SOC 估计出现误差.为了提高状态反馈精度，提出SOCSOH 联合估计，流程如图10 所示.

图10 系统联合估计的流程Fig.10 Process of system joint estimation

根据ECM 和BMS 采集到的数据，通过HPPC 确定初始参数，采用FF-RLS 在线辨识ECM 参数.选取H1、H2、H3、H4 表征因子.采用SVR 建立四维输入的SOH 估计模型，利用PSO 优化选取模型参数.建立基于EKF 的SOC 估计模型，由辨识的ECM 参数实时更新状态空间方程矩阵，通过SOH 修正SOC 估计模型.由2.3 节所推导的估计流程可知，不同SOH 状态下对应的SOC-OCV曲线特征会直接影响参数更新精度，结合3.1 节探究可得SOH 与SOC-OCV 曲线特征相关，可由SOH 实时更新当前状态下的SOC-OCV 关系，修正估计结果.具体如下：在不同的电池老化状态下，由SOH 值修正曲线的7 阶多项式参数，获取精确的SOC-OCV 对应关系.

4 实验验证与分析

4.1 不同测试工况下的状态估计验证

为了验证所提SOC-SOH 联合估计方法的泛用性，对电池采用不同测试工况（DST、FUDS）的数据进行算法验证.电池真实SOC 初始为80%，根据不同的初始估计值对电池SOC 进行估计，其中第630 次循环下标准组电池的估计结果如图11 所示.图中，te为估计时间，SOC0为SOC 的初始估计值.

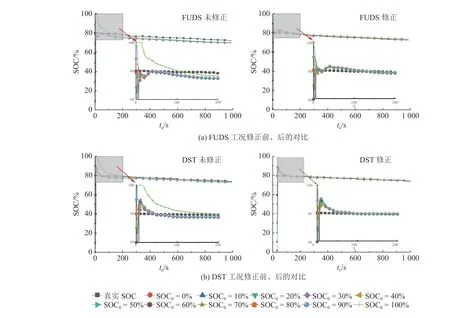
图11 不同测试工况下的电池状态估计结果Fig.11 Battery state estimation results under different testing conditions

以SOC0=70%、DST 工况为例，修正后估计误差由2.47%降为0.92%，不同工况下修正后的收敛时间和精度都得到了优化，证明了算法的通用性.

4.2 不同老化程度下的状态估计验证

为了验证方法的有效性，采用不同老化状态（第450 次循环、第930 次循环）数据进行验证，结果如图12 所示.

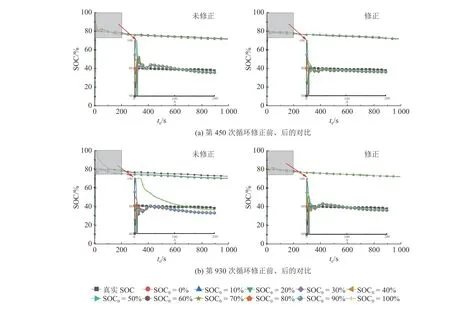
图12 不同老化程度下的电池状态估计结果Fig.12 Battery state estimation results under different aging levels

从第450～930 次循环的结果可以看出，不同老化状态的联合修正都提升了模型的精度，证明了所提方法在电池寿命周期内的有效性.

4.3 状态估计结果的分析

为了量化联合估计算法的修正精度，以系数RMSE 和MAPE 对第630 次循环下的估计效果进行评估，结果如表3 所示.表中，R M S E1、RMSE2分别为第1、2 组标准组电池的RMSE，MAPE1、MAPE2分别为第1、2 组标准组电池的MAPE.

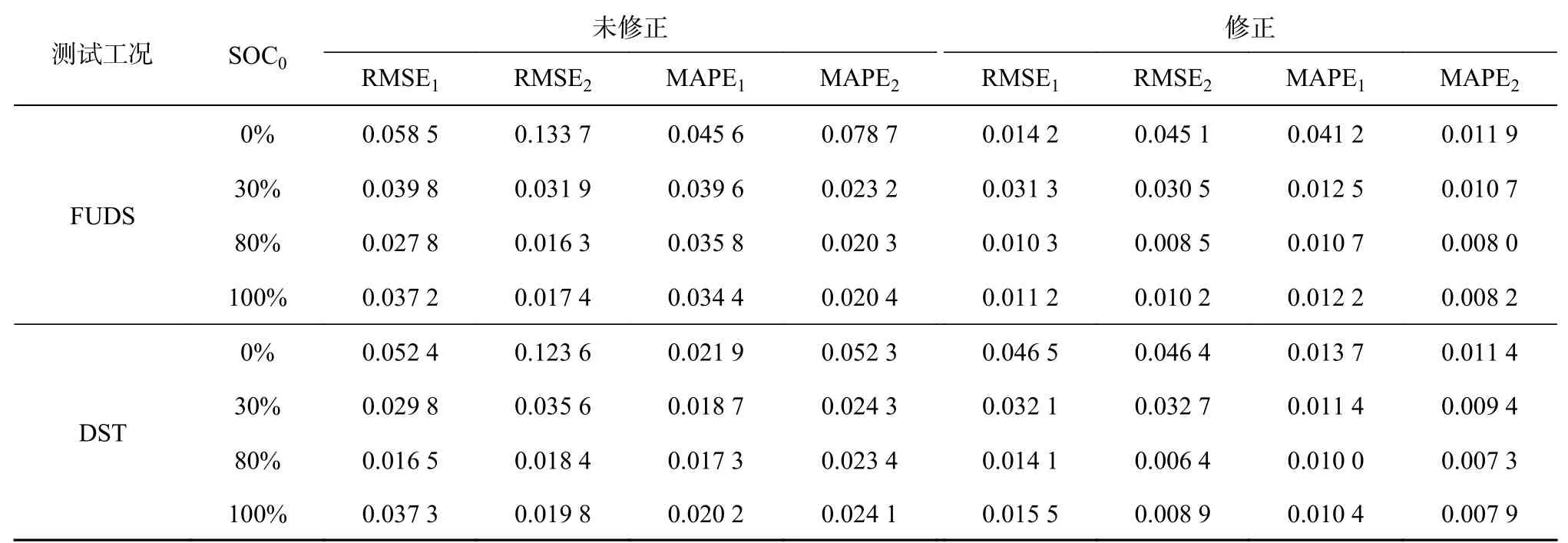
表3 第630 次循环下的状态估计结果对比Tab.3 Comparison of state estimation results under 630th cycle

从表3 可以看出，通过当前的SOH 状态对SOC 估计进行修正后，算法的收敛速度和精度都得到了提升.在FUDS/DST 测试工况下，2 组标准组电池修正前、后的RMSE 和MAPE 都减小了，且无论初始值设置如何，都能够完成SOC 估计.

4.4 真实SOC 的转化

以上是以初始额定容量定义的SOC，该定义不能表示电池在当前状态还能放出多少电量，须进行真实值转化.以充满状态SOC 为100%，可以进行如下转换：

式中：SOCreal为基于当前最大容量定义的SOC，Cn0为初始额定容量，SOCest为估计到的基于初始容量定义的SOC.通过转化可以得到电池当前阶段下的真实状态，提高设备的状态灵敏性.

5 结 论

（1）所提的4 个状态表征因子与电池容量间有较强的相关性，2 组标准电池SOH 估计结果RMSE 分别为0.003 9、0.006 8，MAPE 分别为0.351%、0.610 8%，证明SOH 估计模型具有较好的估计精度.

（2）所提的联合估计方法在不同测试工况下都有较好的效果，2 组电池在630 次循环FUDS 工况下估计的RMSE 由0.027 8、0.016 3 变化为0.010 3、0.008 5，MAPE 由3.58%、2.03% 变化为1.07%、0.8%；在DST 工况下的估计RMSE 由0.016 5、0.018 4 变化为0.014 1、0.006 4，MAPE 由1.73%、2.34%变化为1%、0.73%，证明了方法的通用性.

（3）所提的联合估计方法在不同老化状态下的估计精度都得到了提升，证明了所提方法在电池寿命范围内有较高的可靠性.与其他方法相比，所提的SOC-SOH 联合估计模型可以通过多维的外在表征实时反馈出精确的UUV 内部电池状态，且模型计算复杂度低，对硬件要求不高，可以作为有效的UUV 嵌入式BMS 算法进行应用.