基于LC 并联谐振的轴向自感式位移传感器设计
2024-05-25唐洪洲周瑾金超武徐园平
唐洪洲,周瑾,金超武,徐园平
(南京航空航天大学 机电学院,江苏 南京 210016)
磁悬浮轴承可在无接触的情况下通过改变电磁力控制转子位置,与传统轴承相比,磁悬浮轴承具有无摩擦、免润滑、长寿命、无污染、可主动控制等特点[1-3],广泛应用于航空航天、军事及民用工业领域,如分子泵[4]、机床主轴[5]、鼓风机[6]、压缩机[7]等.在磁悬浮轴承系统中,控制器根据转子位置信号来实时控制磁悬浮轴承线圈中的电流,实现转子的稳定悬浮,所以转子位置信号的获取是磁悬浮轴承系统中的关键因素[8].目前主要采用自传感技术和非接触式位移传感器来获取转子位置.自传感技术的提出使系统的集成度更高,结构更简单,成本降低[9],但该方法依赖于准确的磁悬浮轴承参数,鲁棒性较差,不利于工业应用[10].大多数先进的磁悬浮轴承系统采用位移传感器来检测转子的位移,目前国内外常用的非接触式位移检测传感器有光学位移传感器、电容式位移传感器、电涡流传感器和电感式位移传感器等,光学和电容式位移传感器对工作环境的要求较高,易受灰尘、污垢的影响,应用场景受限[11].磁悬浮轴承系统主要采用电涡流传感器和电感式位移传感器来检测转子位置.与电涡流传感器相比,电感式位移传感器的抗干扰能力更强,不容易受外磁场干扰,还具有高灵敏度、宽测量范围、信噪比高、成本低、信号传输距离长等优点[12],因此更适合应用于高精度磁悬浮轴承系统中的转子位置检测.
国内外很多学者对电感式位移传感器的设计进行了研究,主要包括传感器电感变化的影响因素分析与设计、测量电路设计两方面.传感器电感变化直接影响传感器的性能.Wang 等[13]提出差动式结构,增大了电感变化量,增加了传感器的检测范围,提高了自感式位移传感器的灵敏度和线性度,研究了激励频率对线圈品质因数的影响.Yu 等[14]通过试验研究非机械误差对电感式位移传感器测量精度的影响,提出降低激励频率可以减小测量误差.Ren 等[15]通过引入复磁导率到电感计算模型中,研究涡流效应对自感式位移传感器阻抗变化的影响,分析了不同激励频率下传感器的输出特性.Li 等[16]通过理论推导、仿真与试验,分析气隙长度、匝数对电感式位移传感器电感变化的影响.以上研究都是针对径向电感式位移传感器进行的,针对轴向电感式位移传感器电感变化的影响因素分析与设计,目前还没有相关研究,时振刚等[17-19]只提出了传感器的基本原理.
测量电路的作用是将传感器的电感变化转换成可反映转子位移的直流信号,主要包括调制电路、激励电路与信号调理电路,其中调制电路对传感器的灵敏度具有较大的影响.Wang 等[13,15,18,20]采用半桥电路作为传感器的调制电路,但灵敏度较低.刘亚婷等[21]设计将单个电感与定值电阻串联的方式作为传感器的调制电路,该电路结构简单,其灵敏度相对于半桥电路有所提高,但灵敏度提高有限,不超过半桥电路的2 倍.Hu 等[22]提出全桥式电路,该电路的灵敏度较半桥式电路提高1 倍,但该电路结构复杂,对灵敏度的改善有限.
综上可知,在传统轴向自感式位移传感器的设计方法中,缺少对灵敏度改进的研究.本文提出基于LC 并联谐振的轴向自感式位移传感器,通过增大谐振回路的等效电感变化率,提高传感器的灵敏度.
1 轴向自感式位移传感器的原理
为了改善传感器的线性度,轴向自感式位移传感器采用差动结构,如图1 所示,由转子铁芯、定子铁芯、线圈组成.在通入激励信号后,相邻磁极磁路闭合,形成前排4 个电感和后排4 个电感,即L1~L8.在实际应用中,为了防止转子径向位移对传感器的影响,将前排4 个电感和后排4 个电感分别串联在一起,径向位移对串联后的总电感可以忽略不计,因此可以避免径向位移对轴向位移检测的影响[17].当转子位于轴向平衡位置时,由于传感器差动结构的对称性,前排线圈总电感和后排线圈总电感相等,当转子偏离平衡位置时,电感发生变化,通过测量电路检测出电感变化,进而测量转子位移.

图1 轴向自感式位移传感器的结构图Fig.1 Structure diagram of axial self-sensing displacement sensor
传感器磁路如图2 所示.根据磁路理论可知,线圈电感L 的计算公式为
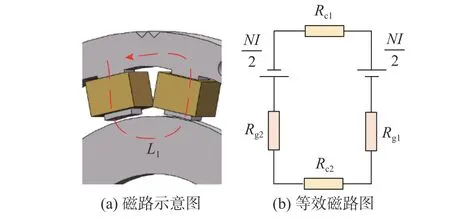
图2 传感器的磁路图Fig.2 Magnetic circuit diagram of sensor
式中:N 为线圈匝数,Rm为磁路总磁阻.
忽略漏磁,磁路总磁阻为
式中:Rg为气隙磁阻,分为Rg1和Rg22 部分;Rc为铁芯磁阻,分为Rc1和Rc22 部分;l1和l2分别为气隙与铁芯的磁路长度;A1和A2分别为气隙与铁芯的磁路面积;μ0为真空磁导率;μr为铁芯的相对磁导率.由于存在边缘效应的影响,当转子沿轴向移动时,气隙磁路长度和磁路面积发生变化,进而磁阻发生变化.此外,由于线圈由kHz 量级的高频电信号驱动产生交变磁场,铁芯表面会在交变磁场中产生涡流,涡流产生的磁场反作用于原磁场,可以将涡流产生的影响看作对铁芯磁导率的影响.对于特定的铁芯材料,涡流效应主要与激励频率有关.当转子位于轴向平衡位置时,线圈电感为
式中:μrf为考虑涡流效应对线圈电感影响的铁芯相对磁导率.转子发生位移后,线圈电感为
式中:Δl1与ΔA1分别为转子发生位移后的气隙磁路长度变化量与磁路面积变化量,可得电感变化率为
从式(5)可知,线圈电感变化率主要与磁路长度、磁极面积、激励频率等因素有关.
由于存在边缘效应、涡流效应、漏磁等因素的影响,线圈电感计算复杂,需要借助有限元仿真,完成轴向自感式位移传感器的设计.
2 有限元仿真
采用Ansys Electronics 软件的涡流场求解线圈电感,计算在边缘效应、涡流效应、漏磁等因素的影响下,线圈电感随转子位移的变化趋势及部分设计参数对电感变化率的影响.
2.1 传感器线圈电感变化特性的分析
传感器的仿真模型如图3 所示.为了提高计算效率,截取了某一对磁极进行分析.对传感器进行参数化建模,分析各设计参数对传感器电感变化率的影响,各设计参数如表1 所示.表中,气隙长度与重叠长度皆为转子处于平衡位置时参数的大小.

表1 传感器设计参数Tab.1 Sensor design parameters

图3 有限元仿真模型Fig.3 Finite element simulation model
如图4 所示为传感器电感变化率ΔL/L0随转子位移δ 的变化.图中,拟合直线的斜率越大,灵敏度越大,均方根误差(root mean square error,RMSE)用于衡量拟合直线与数据点之间的偏差,RMSE越小,线性度越小.可以看出,当δ=-0.5~+0.5 mm 时,ΔL/L0与δ 之间具有较好的线性关系.
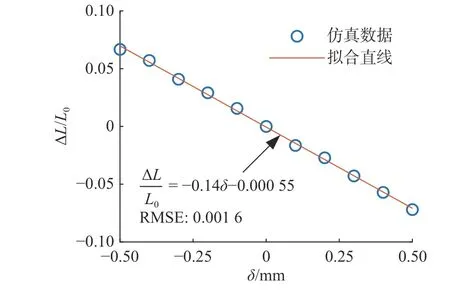
图4 电感变化率随转子位移的变化趋势Fig.4 Trend of inductance variation rate with rotor displacement
2.2 传感器性能影响因素的分析
仿真分析气隙长度、重叠长度、激励频率对电感变化灵敏度的影响.将电感变化灵敏度K 定义为图4 中拟合直线斜率的绝对值.如图5 所示为传感器在不同气隙长度时的电感变化灵敏度.可以看出,随着气隙长度的增大,电感变化灵敏度逐渐降低.如图6 所示为传感器在不同重叠长度时的电感变化灵敏度.随着重叠长度的增大,电感变化灵敏度逐渐降低.如图7 所示为传感器在不同激励频率f 时的电感变化灵敏度,电感变化灵敏度随着激励频率的提高而逐渐降低.

图5 电感变化灵敏度随气隙长度的变化趋势Fig.5 Trend of sensitivity of inductance variation with air gap length
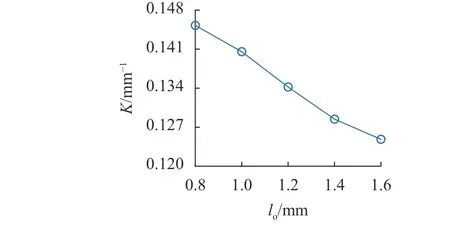
图6 电感变化灵敏度随重叠长度的变化趋势Fig.6 Trend of sensitivity of inductance variation with overlap length
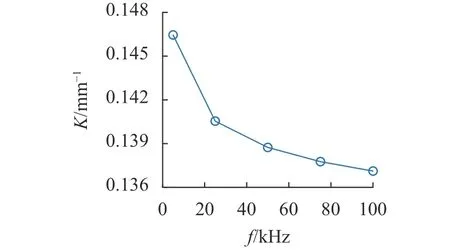
图7 电感变化灵敏度随激励频率的变化趋势Fig.7 Trend of sensitivity of inductance variation with excitation frequency
综上所述,为了提高传感器的灵敏度,应在考虑保护轴承间隙(转子运动范围)及转子径向位移对传感器输出影响[19]的基础上,尽量减小气隙长度与重叠长度.本文所设计的传感器在实际应用中,转子沿径向运动范围为-0.125~+0.125 mm,沿轴向运动范围为-0.5~+0.5 mm,因此气隙长度设计为0.5 mm,重叠长度设计为1 mm.激励频率不仅与电感变化率有关,还与调制电路的设计有关,所以激励频率的设计将在3 章中继续讨论,在此初步定为25 kHz.
3 测量电路设计
为了获取转子位移信号,采用测量电路将转子位移信号转换为直流信号.
测量电路如图8 所示,主要包括以下3 个部分.第1 部分为激励电路,给线圈提供稳定的交流激励信号.第2 部分为调制电路,将转子位移变化转换成电压或电流信号.第3 部分为信号调理电路,将调制信号调节为与转子位移成比例的直流电压信号.
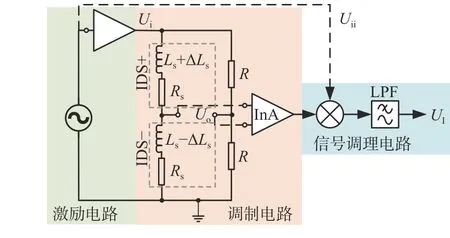
图8 测量电路的示意图Fig.8 Schematic diagram of measurement circuit
对于传感器电感变化的测量,通常采用电桥电路,电路结构简单,准确度高.
为了从调制信号Uo中获取转子位移信号,需要对其进行解调处理.假设输出电压Uo=Uom×cos (ωt+θ),载波Uii=Umcos (ωt)(其中Um为载波幅值),通过乘法器后,可得一高频分量和一直流分量:
通过低通滤波器滤除高频分量,得到直流分量:
当Um固定不变时,UI的变化可以反映输出电压Uo的幅值及相位的变化.输出电压实部反映了电感的变化,采用0°相位角的载波信号Uii可以获得Uo的实部,消除了其他频率成分信号的干扰[23].在实际应用时,UI经偏置电路与放大电路处理后,由ADC 进行采集.
为了进一步提高灵敏度,采用LC 谐振和差动线圈置于不同桥臂的方法,基于差动半桥电路的拓扑结构设计图9 所示的3 种电路(电路A、B、C).图中,IDS+与IDS-分别为传感器前排与后排线圈串联,电路A 是最基本的差动半桥电路,差动线圈在相同桥臂,线圈两端没有并联电容.电路B 和电路C 都在线圈两端并联了电容,选择在激励频率附近谐振,综合考虑灵敏度与线性度,由谐振频率计算公式可得,电容确定为Cp=1/[4Lmax(πf)2],其中Lmax当δ=-0.5~+0.5 mm 时线圈电感的最大值.电路B 为差动线圈在相同桥臂,电路C 为差动线圈在不同桥臂,电阻R0=ωLeq,其中Leq为LC 谐振电路的等效电感.
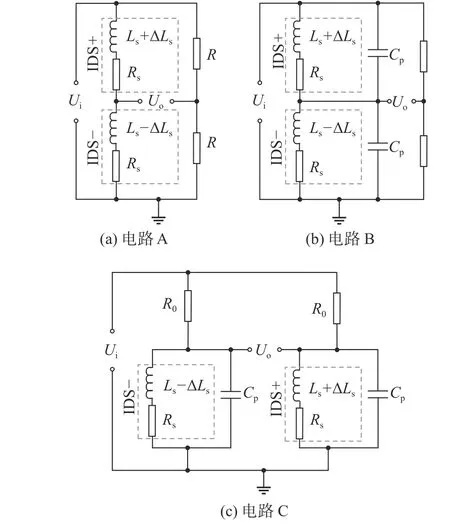
图9 调制电路的拓扑结构Fig.9 Topology of modulation circuit
为了说明改进差动半桥电路拓扑结构对传感器灵敏度的影响,分析图9 所示3 种电路的灵敏度.
为了简化分析,将LC 谐振电路等效为一个电阻和一个电感串联,如图10(b)所示.LC 谐振等效电路阻抗可以表示为
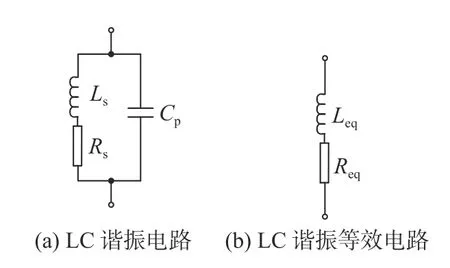
图10 并联谐振电路Fig.10 Parallel resonance circuit
假设Rs很小,忽略不计.等效电感为
若线圈电感增加了ΔLs,且假设ΔLs<<Ls,则谐振电路等效电感的变化率为
当谐振频率接近激励频率时,0<|1-ω2LsCp|<1.0,可得等效电感变化率与传感器线圈电感变化率之间的大小关系为
因此使用谐振电路可以增大传感器的灵敏度,为了进一步提升传感器的灵敏度,提出将差动线圈置于不同桥臂的配置方式.若IDS+电感增加了ΔLs,IDS-电感减小了ΔLs,则电路B 的输出电压为
电路C 的输出电压为
从式(10)、(11)可知,电路C 的灵敏度更高,为电路B 的2 倍.
为了确定最合适的调制电路及最佳的激励频率,结合ANSYS Electronics 和MATLAB,对滤波电路的输出电压进行数值仿真分析.线圈电感由ANSYS Electronics 计算,采用MATLAB 计算滤波电路输出电压信号实部Re{Uo}.从Ui到Uo的传递函数为G(s),即Uo=G(s)Ui,本节主要分析调制电路的特性,假设Ui=1 V.
如图11~13 所示为3 种不同的调制电路在不同激励频率下输出电压随δ 的变化关系图.可知,电路B 的灵敏度约为电路A 的8 倍,电路C 的灵敏度约为电路B 的2 倍,约为电路A 的16 倍,与理论推导符合,因此采用电路C 作为传感器的调制电路,以获得更高的灵敏度.
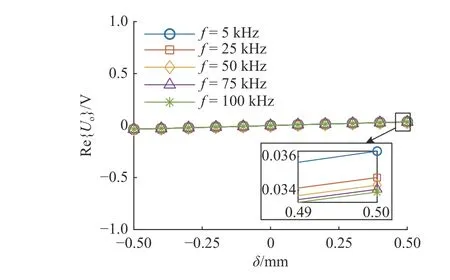
图11 电路A 在不同频率下输出电压随位移的变化Fig.11 Variation of output voltage with displacement at different frequencies for circuit A
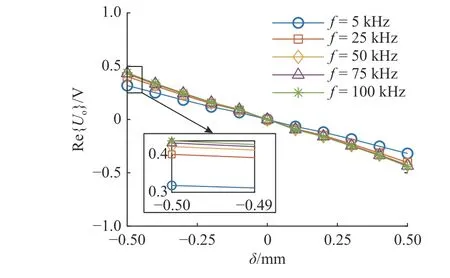
图12 电路B 在不同频率下输出电压随位移的变化Fig.12 Variation of output voltage with displacement at different frequencies for circuit B

图13 电路C 在不同频率下输出电压随位移的变化Fig.13 Variation of output voltage with displacement at different frequencies for circuit C
为了选择最佳激励频率,分析电路C 在不同激励频率下的灵敏度Ko与RMSE.如表2 所示,激励频率越大,灵敏度越大,线性度越大.此外,传感器的带宽必须足够高,激励频率与传感器的带宽直接相关[24],一般传感器的截止频率为激励频率的1/10~1/5[25],所以激励频率不宜太低.综合考虑,激励频率选择为25 kHz.

表2 不同激励频率下的灵敏度与RMSETab.2 Sensitivity and RMSE at different excitation frequencies
电容Cp=1/[4Lmax(π fres)2],其中fres为谐振频率.为了增大传感器的灵敏度,使谐振频率尽量靠近激励频率.谐振频率与传感器性能相关,为了研究谐振频率相对于激励频率变化时传感器的特性,开展如下分析.如图14 所示,通过改变fres,在较大的频率范围内,δ 为-0.5~-0.1 mm,输出电压变化远大于差动半桥电路的输出电压变化(0.036 V),即灵敏度远大于差动半桥.分析不同谐振频率下传感器的输出电压随位移的变化关系,灵敏度和RMSE 如表3 所示.可知,谐振频率越靠近工作频率,灵敏度越大,线性度越差.综合考虑灵敏度与线性度,选择合适的谐振频率.
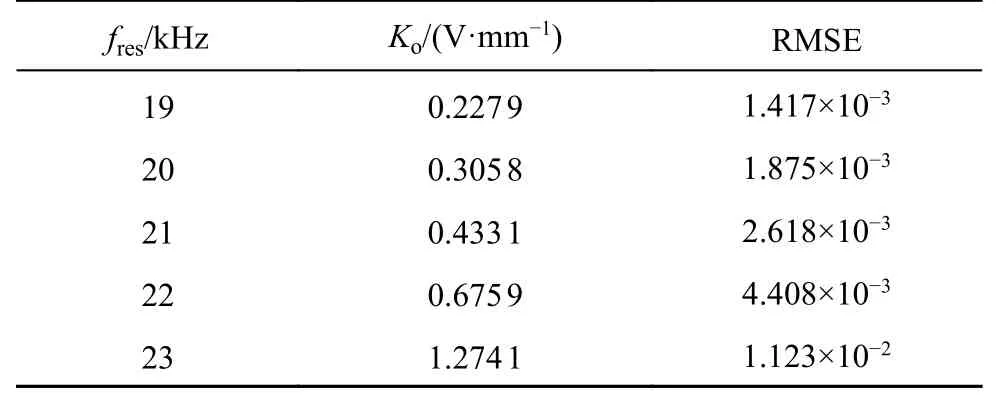
表3 不同谐振频率下的灵敏度与RMSETab.3 Sensitivity and RMSE at different resonant frequencies
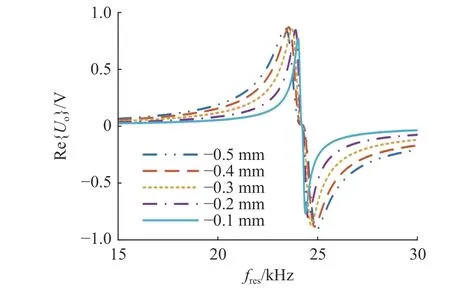
图14 不同谐振频率下输出电压的变化特性Fig.14 Output voltage variation characteristics at different resonant frequencies
4 实验分析
为了测试轴向自感式位移传感器的电感变化特性,设计电感变化测试平台.如图15 所示,通过标定台改变转子位置,采用阻抗分析仪IM3570 测量不同位置下的传感器线圈电感.如图16 所示,线圈电感的变化率与转子位移之间的线性关系较好,电感变化灵敏度与有限元仿真基本一致.

图15 电感变化测试平台Fig.15 Inductance variation test platform

图16 电感变化率随转子位移的变化趋势Fig.16 Trend of inductance variation rate with rotor displacement
传感器静态性能的测试平台如图17 所示.测量电路中的激励电路输出激励电压信号Ui给传感器,传感器输出电压信号Uo,测量电路对Uo处理后,获得反映转子位移的直流电压信号UI,采用示波器测量该信号的幅值.位移为-0.5~0.5 mm,每0.05 mm 记录一次数据.

图17 静态性能测试平台Fig.17 Static performance test platform
如图18 所示为不同轴向位移时传感器的输出特性.传感器的灵敏度为拟合直线的斜率,即24.49 V/mm,实验数据点与拟合直线之间的最大偏差ΔLmax为0.058 V,满量程输出值YFS为24.49 V,线性度为

图18 传感器的输出特性Fig.18 Output characteristics of sensor
如图19 所示为迟滞性曲线,正行程和反行程之间的最大偏差ΔHmax为0.15 V,迟滞性为
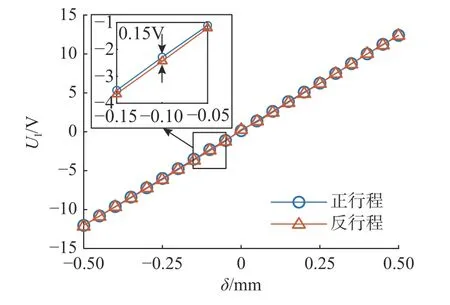
图19 迟滞性曲线Fig.19 Hysteresis curve
如表4 所示,相对于其他位移传感器,该传感器具有更高的灵敏度与更低的线性度,迟滞性小于1%,因此该传感器满足磁悬浮轴承系统面向更高精度的发展需求.
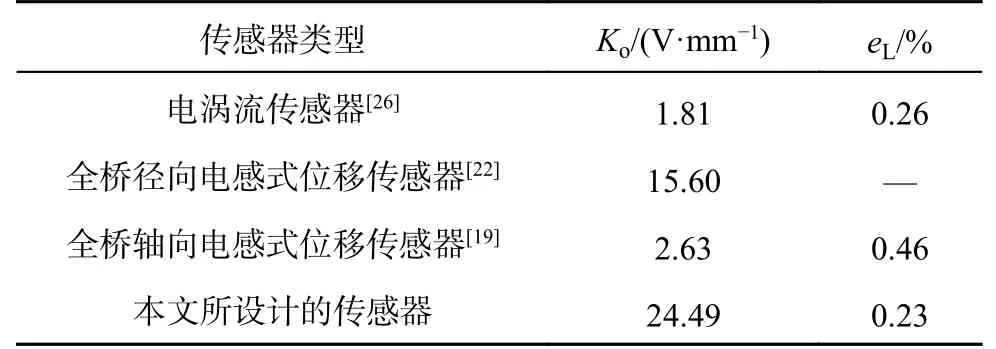
表4 本文所设计的传感器与其他类似传感器的比较Tab.4 Comparison of sensor designed in this paper with other similar sensors
5 结 论
(1)为了提高传感器的灵敏度,应在考虑转子运动范围的基础上,尽量减小气隙长度与重叠长度.
(2)基于LC 并联谐振的调制电路可以通过提高谐振回路的等效电感变化率,增大传感器的灵敏度.
(3)线圈的激励频率与谐振频率的选择会对传感器的灵敏度与线性度产生影响.
(4)实验结果表明,在测量范围-0.5~0.5 mm 内,传感器的灵敏度为24.49 V/mm,线性度为0.23%,迟滞性为0.61%,满足磁悬浮轴承面向更高精度的发展需求.
本文所设计的轴向自感式位移传感器为磁悬浮轴承系统拓展了更广阔的应用领域,需要进一步研究其稳定性和抗干扰能力.
