驻留式微气泡阵列流动减阻机理数值研究
2024-05-25朱睿何星宇赵晨鸿刘宇张焕彬陈腾飞谭鑫刘志荣
朱睿,何星宇,赵晨鸿,刘宇,张焕彬,陈腾飞,谭鑫,刘志荣
(1.厦门大学 航空航天学院,福建 厦门 361005;2.西藏民族大学 信息工程学院,陕西 咸阳 712082)
水下航行体的阻力主要有兴波阻力、压差阻力和摩擦阻力[1].调整形体和流线型可以改善兴波阻力和压差阻力,而低速时航行体的摩擦阻力约占总阻力的80%~90%[2].随着数值计算和科学试验的发展,对摩擦阻力的机理研究愈发深入.改变流体介质运动特性和边界层内近壁区流场特性可以大幅减小航行体的摩擦阻力,是未来流动减阻技术的发展方向.
微气泡减阻技术的试验和数值结果显示其良好的性能和应用潜力,已成为水下减阻领域的研究热点[3-7].Kim 等[8]研究水翼表面在不同弗劳德数下的喷气减阻特性,利用高速相机量化了气泡注入量,取得了一定的减阻效果.Mohammed 等[9]采用数值方法研究集装箱船模型在不同工况下的喷气微气泡减阻效果,结果表明当弗劳德数为0.282,空气体积分数为4.8%时,最高减阻率达到27.6%.Jha 等[10]测试了不同气泡空隙率α=0~0.15、雷诺数Re=22 500~67 500 及气泡喷射方向下水平紊流单通道的流动阻力,结果显示,顶壁喷射能够减少最高60%的阻力.陈正云等[11]通过试验观测,得到不同超疏水表面形成的表面气膜具备良好的稳定性和减阻性能,减阻率可达30%.姚琰等[12]通过试验测量了多孔喷气平板表面在不同通气量和来流速度下的切应力,结果显示微气泡在浮力作用下形成边界层气膜,最大减阻率可达36%.宋武超等[13]通过试验研究不同俯仰状态下航行体表面的微气泡形态及减阻特性,结果显示,微气泡附着受通气量、重力和来流速度的影响,减阻率随着航行体攻角的变化呈现正弦变化.
当前,主流微气泡减阻方式通常是通过近壁区通入大量自由气泡,但这种通气式微气泡无法稳定留在近壁区边界层.微气泡研究主要集中于减阻效应,气液两相流演化非常复杂,尚缺乏完善的减阻机理理论[14-19].Zhu 等[20-21]在前期已完成微气泡阵列流动减阻性能试验的研究,提出自稳式电解微气泡阵列气膜减阻技术;遴选出较优的微柱孔阵列形状(直径d=250 μm,间距比d/l=1.25,径深比d/h=2),在0.3~1.0 m/s 流速下减阻率可达18%~30%.本文采用大涡模拟(large eddy simulation,LES),构建平板及驻留微气泡2 种模型下的近壁区边界层湍流数值模型.基于湍流数值计算数据,利用本征正交分解(POD)方法进行模态分析,提取各阶模态所占的能量和对应的流场结构,开展驻留式微气泡近壁面湍流流场演化特性、湍流特征参数及减阻机理分析,揭示驻留式微气泡对湍流边界层内流场演化特性的影响机制,完善微气泡减阻机理.
1 数值模拟
1.1 数值求解方法
由于湍流流动为非线性的复杂流动,流体内存在大小不同的涡流和涡旋,大多数工程问题中的流体流动均处于湍流状态.一般认为即使湍流运动非常复杂,非稳态的连续方程和Navier-Stokes 方程仍然适用于湍流的瞬时运动[22].Navier-Stokes 方程的非守恒形式为
式中:ϕ为通量,ρ为流体密度,t为时间,u、v、w为瞬时速度在x、y 和z 方向的分量,Γ为广义扩散系数,S 为源相.
目前,湍流数值模拟方法可以分为直接数值模拟方法(DNS)和非直接数值模拟方法,其中非直接数值模拟方法包括雷诺平均法(RANS)及大涡模拟(LES).大涡模拟是介于DNS 与RANS 方法之间的湍流数值模拟方法[23],基本思想是直接模拟大尺度湍流运动,小尺度湍流表示为亚格子尺度(SGS)湍流模型.为了解析湍流下平板及驻留式微气泡阵列近壁边界层区域的精细流场特性,采用大涡模拟作为流场特性分析所使用的湍流模型.
在LES 中,SGS 模型为未分解的湍流运动提供了封闭初始解.根据Smagorinsky[24]的基本SGS 模型,假定SGC 具备以下形式,得到Smagorinsky-Lilly 模型.
式中:τij为亚格子尺度应力;τkk为亚格子尺度应力张量的迹;δij为克罗内克数;µt为亚格子尺度的湍流黏度;Δi为沿i 轴方向的网格尺寸;Cs为Smagorinsky 常数,通常取0.17;为组成的张量.
1.2 平板及驻留微气泡流动的数值模拟
如图1 所示为光滑平板及带有驻留微气泡阵列表面平板计算域及网格划分示意图,计算模型区域大小为L×H=70 mm×10 mm,驻留式微气泡由微柱孔底部通气形成.微柱孔参数采用文献[25]所述,其中微柱孔深度h=125 μm,直径d=250 μm,间距l=200 μm,计算域内共布置9 个微气泡阵列.采用多块结构化网格,对湍流边界层及微气泡附近区域网格进行加密(近壁面法向第1 层网格高度y+< 1,网格增长率为1.05),整体网格数为4.5×106.

图1 平板及驻留微气泡的计算域与网格划分Fig.1 Computational domain and mesh division of plate and resident microbubbles
为了使边界层能够在较短距离内模拟完全发展的湍流结构,采用Sandham 等[26]提出的在边界层内统一的随机函数扰动的方法生成湍流边界层,计算域的边界条件设置如下.其中计算域入口设置为速度入口,使用用户自定义函数(UDF)自编译平均入口速度与内外层扰动速度叠加的流向速度.入口平均速度曲线方程如下所示:
式中:uτ为壁面剪切速度,y 为壁面高度,ν为流体运动黏度.
入、出口流向及展向扰动速度函数如下.
式中:y+为壁面无量纲高度,y+=yuτ/ν ;yp,j为扰动达到峰值时的壁面高度,下标j 为扰动模式序号;ci,j为扰动常数;ωj为扰动频率,φj为相位移,j=0、1、2、3.
计算域出口设置为压力出口,上壁面采用自由滑移壁面边界条件,下壁面采用无滑移壁面边界条件.
微气泡水下动态形变过程涉及气/水两相流演变,故在数值计算时采用基于体积分数法(volume of fluid,VOF)的气/水两相流模型.本文基于大涡模拟(large eddy simulation,LES)模型、VOF 气/水两相流模型,构建平板及驻留式微气泡流动数值模型.在FLUENT 软件中采用压力基隐式瞬态求解器,控制方程在离散计算单元中求解,采用SIMPLEC 算法求解压力-速度耦合,压力项空间离散采用PRESTO!格式,动量、湍动能及湍流耗散率均使用2 阶迎风格式.为了保证计算精度,将非定常计算时间步长设置为0.000 1 s,每个时间步迭代25 次以保证解的收敛,且库朗数小于0.5.设置计算总时长为0.2 s,使得流动达到稳定完全发展湍流状态后,提取0.2 s 的数据样本进行统计分析.
1.3 数值模拟有效性的验证
湍流边界层的平均速度分布有3 个典型的区域:线性底层、过渡区和对数区.线性底层与对数区均存在强烈的湍流脉动.在平板边界层发展为完全湍流后,对整体流场在时间、空间尺度上采取时均统计学处理,提取流向位置x=20δ 时(其中δ 为边界层厚度,δ=1.45 mm)沿壁面法向上的平均流向速度与相同雷诺数下(Reθ=1 430,θ 为边界层动量厚度)De Graaff 等[27]的试验数据进行比较.图2 给出时均统计后平板湍流边界层内沿法向的平均速度分布.图中,< >表示非定常变量的时间平均结果,U+为无量纲速度,
图2 平板湍流边界层内法向平均速度与试验数据的对比
Fig.2 Comparison of normal average velocity in plate turbulent boundary layer with test data
式中:ρw为水的密度,τ0为壁面切应力.
如图2 所示,平板湍流边界层的数值计算结果与试验值吻合较好,平均误差小于20%.误差的产生原因主要有介质不同(空气与水)、环境因素影响(温度、气压)及仿真模型维度不匹配,导致数值计算结果与试验数据有一定的差异.
图3 给出平板湍流边界层内的各向湍流脉动强度,采用统计学方式提取脉动速度的均方根(RMS),反映了湍流的强度.图中,urms+、vrms+分别为流向及法向的无量纲湍流脉动速度的均方根.从图3 可以看出,平板边界层的各向湍流脉动强度呈现先升后降的趋势,在边界层边缘逐渐下降至0,峰值均出现在y/ δ=0.022 左右的位置;边界层内区的脉动强度高于外区,这是由于内区速度梯度大,流速变化较大,使得内区流体受到更强的切应力作用,促使流体出现较强的脉动.将湍流脉动强度与Spalart 等[28-29]的直接模拟(DNS)结果进行比较,平均误差均小于15%,结果保持一致,验证了所用数值方法的可靠性.

图3 LES 与DNS 湍流脉动强度的对比Fig.3 Comparison of turbulent pulsation intensity between LES and DNS
2 POD 方法
POD 方法是将高维数据降维的方法,它的核心是基于数据的协方差矩阵进行特征值分解和特征向量提取的过程.具体来说,对于包含 n 个样本或快照的数据集合,可以将其表示为 m×n的矩阵A,其中 m 为每个样本的维度.计算 A的协方差矩阵 C=ATA,对其进行特征值分解.通过特征值和特征向量的排序和截断,可以将数据集合的信息压缩到低维的子空间中.这个子空间中的基向量由协方差矩阵的前r 个特征向量构成,其中 r 为要保留的主要特征向量的数量.采用这些基向量来表示原始数据集合中的每个样本,得到其在低维子空间中的表示.由于本征向量是正交的,在低维子空间中表示的数据具有良好的可解释性和可视化性.
通过所提取的各瞬时时刻流场信息(速度)集计算出时均流场信息,将瞬时流场信息减去时均流场信息,获得每个时刻的脉动速度矩阵.采用POD 方法,将脉动速度矩阵分解为正交模态和时间系数,如下所示:
式中:u′(X,t)、u(X,t)和(X,t)分别为某时刻下流场脉动速度矢量场矩阵、瞬时速度矢量场矩阵和时均速度矢量场矩阵;ak(t)为该流场时间系数;φk(X)为分解得到的第k 阶模态;N 为提取的流场时刻样本数,N=200,保证了POD 方法湍流特征统计量的稳定性.
对该流场脉动速度矢量场矩阵分解得到的对应正交基的能量排序,可得第k 阶POD 模态的能量与总流场能量的占比,如下所示:
式中:λk为第k 阶模态对应的特征值.
3 计算结果及POD 分析
3.1 平板流场及驻留微气泡流场的演化特性
虽然传统通气式微气泡减阻方式能够达到约30%的减阻率,但存在减阻效果不稳定及需要不断通气的问题;驻留微气泡阵列兼具良好的稳定性与减阻性能.图4 给出流场演化过程中平板及驻留微气泡阵列表面在x=15δ~25δ 位置的壁面切应力τ 分布曲线,其中无量纲时刻t+=t/t1(t1为流场演化的时间0.2 s,t 为流场演化过程中的各个时刻).如图4 所示,驻留微气泡阵列表面湍流边界层平均壁面切应力约为1.23×10-3N,相较于平板减少了约13.7%,验证了驻留微气泡阵列具备一定的减阻性能.在微气泡气/水界面动态形变及湍流特性的影响下,表面壁面切应力呈现动态振荡特性,相较于平板在t+≈ 0.52 时刻下的突变,微气泡阵列表面的切应力表现得更稳定.

图4 平板及微气泡阵列表面壁面切应力分布Fig.4 Wall shear stress distribution of plates and surface of microbubble arrays
以往对近壁面湍流相干结构的研究表明,在一对正、负的流向涡旋之间存在低速条带[30],如图5 所示.流向涡旋上冲侧带离壁面的低速流体称为上抛,流向涡旋下冲侧带向壁面的高速流体称为下扫,这些向上和向下的流体运动被称为湍流相干结构猝发.流向涡结构内高速流体的下扫产生的近壁面雷诺切应力是近壁面湍流摩擦阻力的主要来源.
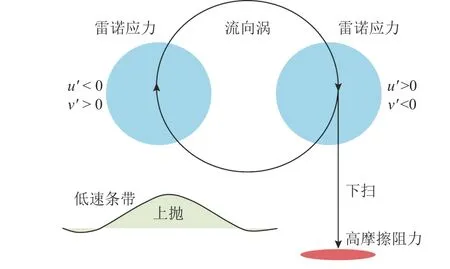
图5 上抛、下扫猝发[30]Fig.5 Upcast,down-sweep burst[30]
图6(a)~(d)给出不同时刻平板湍流边界层流向速度场u 的演化云图.如图5 所示,完全发展的湍流平板边界层内速度分布不再呈现时均流场下稳定的边界层,而是形成多个低速流体突起与高速流体下凹,平板湍流边界层存在低速回流涡结构.如图6(e)所示为该低速区速度矢量图.可以看出,该区域呈现低速流体上抛与高速流体下扫的“猝发”现象,形成湍流相干结构.从图6 还可以看出,随着时间的迁移,速度分布突起从上游逐渐迁移至下游,当t+≈ 0.5 时,流向涡结构迁移至x=15δ~25δ 位置,与平板切应力突变节点相对应.
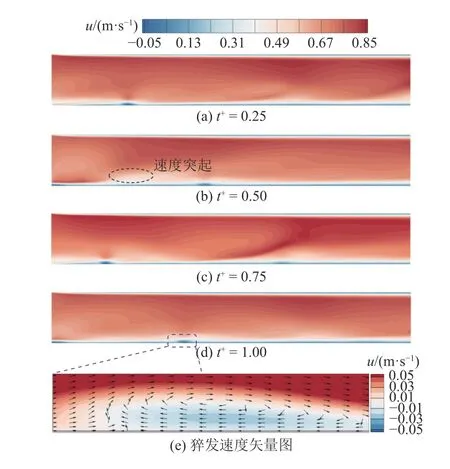
图6 不同时刻平板湍流边界层流向速度场Fig.6 Flow velocity contour of plate turbulent boundary layer at different time
图7(a)~(d)给出驻留式微气泡阵列表面不同时刻流向速度u 的演化云图.可以看出,驻留式微气泡阵列的存在使得整体速度场更均匀,边界层内流向涡在流经微气泡后消失,表明微气泡阵列可以破坏湍流相干结构.如图7(e)所示为微气泡阵列表面速度矢量.可以看出,驻留微气泡动态形变下其柔性气/水界面处存在丰富的涡系结构,微气泡前部与后部存在对称、旋向相反的涡旋,前部形成的逆时针旋转涡旋表现为高速流体上抛、低速流体下扫,抑制“猝发”.微气泡后部形成的涡旋方向虽然与相干结构一致,但其直径较平板流向涡减小了约80%.从图7(e)还可以看出,气/水界面动态形变使其曲率不断变化,微气泡表面微曲率导致的康达效应减弱,微气泡后部形成流动分离,在下一个微气泡前部形成再附着.如此产生的涡系结构极大程度地破坏了湍流边界层分布的连续性,减少了微气泡阵列边界层内高摩擦阻力的产生.
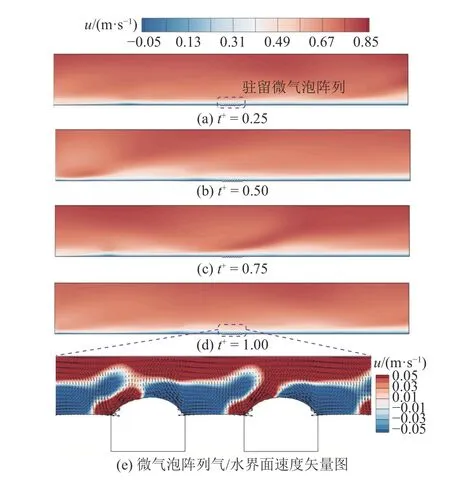
图7 不同时刻微气泡阵列表面流向速度云图Fig.7 Flow velocity contour of surface of microbubble array at different time
图8 给出不同时刻平板及驻留微气泡阵列表面在湍流边界层内(x=20δ,y+=10)流向及法向的无量纲速度u+、v+演化曲线,据此分析微气泡阵列对湍流相干结构“猝发”的量化影响机制.如图8所示,平板湍流边界层内流向速度及法向速度的幅值均大于微气泡阵列表面,存在明显的周期性演化.该速度演变周期为湍流相干结构“猝发”周期.通过对法向速度演化实施傅里叶变化(FFT),得到频谱图,如图9 所示.图中,vma为平板及微气泡阵列表面法向速度的幅度.从图9 可以看出,平板法向速度主频率(8.77 Hz)与主频所在幅值(59.87 m/s)均大于驻留微气泡阵列表面主频率(3.17 Hz)与幅值(16.78 m/s),说明微气泡阵列的存在将“猝发”频率有效降低了63.85%,达到了约13.7%的减阻效果.
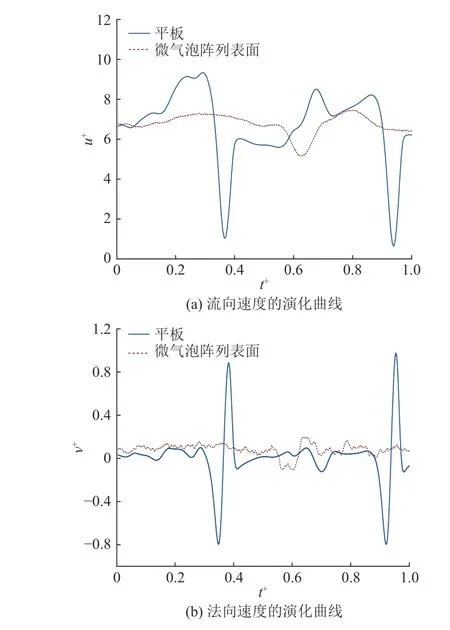
图8 不同时刻平板及微气泡阵列表面速度演化Fig.8 Velocity evolution of plates and surface of microbubble arrays at different time

图9 平板及微气泡阵列表面法向速度频谱图Fig.9 Spectrum of normal velocity on plate and surface of microbubble array
如图10 所示为平板与微气泡阵列表面边界层近壁面相同区域内统计得到的平均湍动能TKE 演化曲线.可以看出,微气泡阵列结构使得近壁面湍动能较平板减少(微气泡阵列气膜平板表面平均湍动能为0.093 m2/s2,平板表面平均湍动能为0.165 m2/s2),减少了湍流与近壁面之间的能量交换,降低了流体与壁面之间的相互作用.
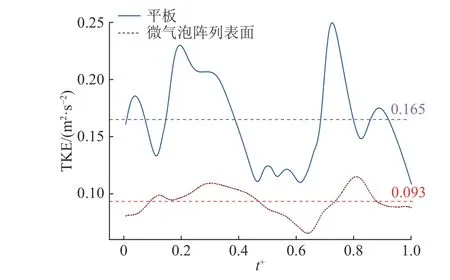
图10 平板及微气泡阵列表面湍动能演化Fig.10 Turbulence kinetic energy evolution of plate and surface of microbubble array
3.2 流场演化POD 分析
采用POD 方法,对应用大涡模拟方法得到的湍流边界层流场特征结构进行降阶处理.选取流场范围为长度L1=40 mm,高度H1=6 mm,流场演化时间t1=0.2 s,各个瞬时时刻间隔Δt1=0.001 s,将时间划分为200 个样本.流向速度u 与法向速度v 的样本空间大小为1 001×601,生成201 个快照向量矩阵,从而得到201 个POD 基向量.通过对流场二维速度矢量场进行POD 分解,求解得到流场速度的旋度(即涡量),分析湍流边界层内拟序结构的演变规律.
图11 给出基于POD 方法分解得到的光滑平板与微气泡阵列表面湍流边界层内第0 阶模态(平均流场)云图.图中,ωa为涡量.从图11 可以看出,采用POD 分解得到的平均流场云图与时均化流场边界层结构高度一致,流场稳定性较强.在光滑平板边界层内,总体涡量强度相较于微气泡表面高.在微气泡阵列区域,涡量强度较高,表明微气泡的存在破坏了湍流边界层内原有的结构.
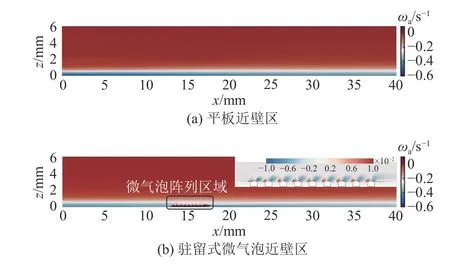
图11 0 阶模态/平均流场Fig.11 Zero order/average flow field
图12 给出二维平板速度矢量场经POD 分解后得到的前20 阶模态总能量累积占比Pc分布曲线.可以看出,平板边界层达到总体湍流能量的90%需要11 阶的模态,而微气泡阵列表面只需要前7 阶模态,这说明微气泡的存在使得平板边界层内的湍流流场结构更稳定,总体减少了湍流拟序结构.图13 给出单独各阶模态的能量占比Pk情况,其变化规律随阶数的增加而减少,最终趋于0.将平板二维速度矢量场分解至10 阶模态,可以完整重构原有流场.
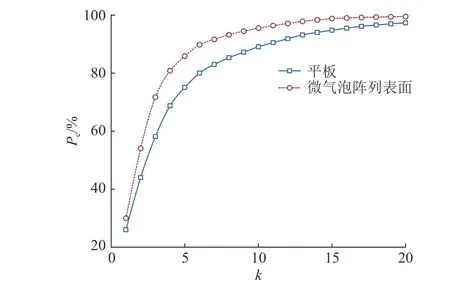
图12 各阶总能量累积分布曲线Fig.12 Cumulative distribution curve of total energy of each order
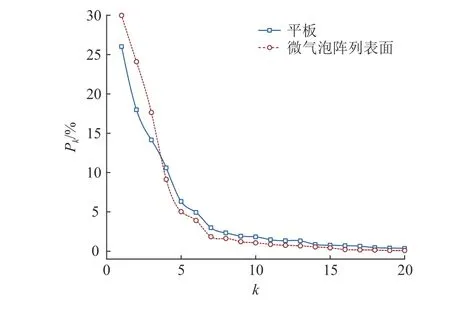
图13 各阶能量占比变化曲线Fig.13 Variation curve of energy proportion for each order
图14、15 分别给出完全发展的平板湍流边界层与微气泡阵列气膜边界层二维速度矢量场前10 阶模态分解云图.可以看出,随着模态阶数的增加,平板湍流边界层内涡旋结构逐渐失稳,涡量强度增大,到第7 阶模态出现典型的湍流相干拟序结构,涡团结构呈现正负交替对称分布,遍布整个平板边界层,与3.1 节所述流向涡的“猝发”过程一致,形成高摩擦阻力.对比微气泡阵列气膜下各阶模态的分解云图可知,微气泡的存在对整体平板拟序结构具备强烈的破坏性,微气泡阵列气膜表面涡旋结构形态更扁平,湍流特征结构在壁面法向阵列表面的拟序结构较光滑平板明显减少,相应受到抑制.对比图14(e)、15(e)的第9 阶模态可见,微气泡近壁区的切应力降低,表现出良好的减摩特性.
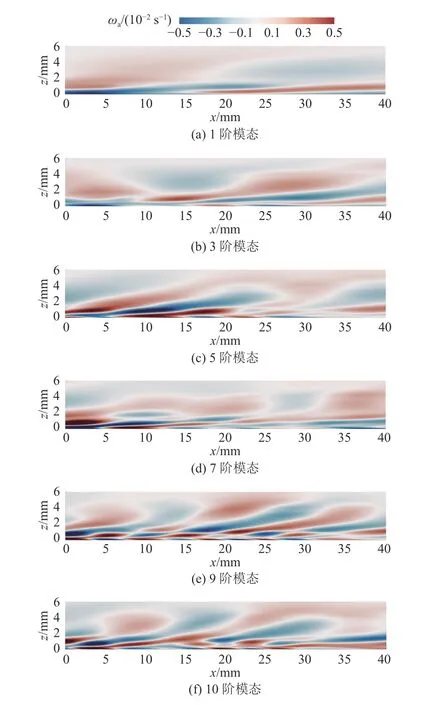
图14 平板湍流边界层的模态云图Fig.14 Modal nephograms of turbulent boundary layer on plate
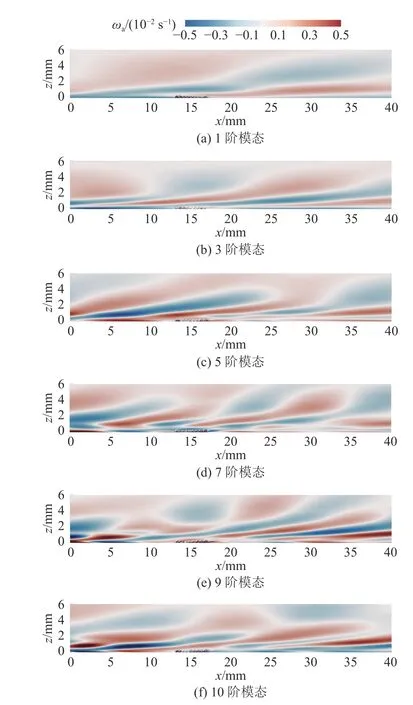
图15 微气泡阵列表面湍流边界层的模态云图Fig.15 Modal nephograms of turbulent boundary layer on surface of microbubble array
图16 给出典型阶数下微气泡阵列气膜的模态局部云图.可以看出,微气泡阵列局部大尺度涡旋结构显著减少,加强了湍流区域内的小尺度结构,使得流场内的湍流动能分布更均匀,抑制了湍流拟序结构的发展,在边界层内形成良好的减阻效果.

图16 局部微气泡阵列表面湍流边界层的模态云图Fig.16 Modal nephograms of turbulent boundary layers on surface of local microbubble arrays
4 结 论
(1)微气泡阵列(直径d=250 μm、间距比d/l=1.25 及径深比d/h=2)的存在使得近壁区切应力减小约13.7%,流向涡尺度降低约80%,削弱了动量交换,降低了湍动能与动量耗散.
(2)流向涡的发展、迁移带动边界层内低速流体上抛、高速流体下扫,形成“猝发”现象,是平板湍流边界层内高摩擦阻力的本质原因.
(3)驻留微气泡的存在可以破坏湍流相干结构,使得“猝发”频率由8.77 Hz 降低至3.17 Hz,脉动速度幅值随之降低.
(4)利用POD 方法,能够有效地提取湍流拟序结构,微气泡的存在使得平板表面涡旋结构形态更扁平,加强了湍流区域内的小尺度结构,使得流场内的湍流动能分布更均匀,抑制了相干结构的发展.将驻留微气泡应用于水下航行体以提升表面减阻性能是下一阶段研究的重点.
