基于网格空间团的多级同位模式挖掘方法

刘宇情，王丽珍，杨培忠，朴丽莎

(1.云南大学 信息学院，云南 昆明 650504；2.滇池学院 理工学院，云南 昆明 650228)

随着遥感技术、空间定位系统和智慧城市等地理信息处理技术的快速发展，空间数据量与日俱增.空间数据中隐藏着无数有价值的知识，如何挖掘这些知识并应用到实际生活变得至关重要.作为空间数据挖掘的一个重要分支，空间同位模式挖掘旨在从空间数据中发现空间特征之间的关联关系.空间同位模式是空间特征集的一个子集，其实例频繁出现在彼此的邻域中，互为邻居.空间同位模式挖掘近年来得到了发展，并在许多领域得到了广泛的应用，例如公共安全[1]、公共健康[2]、生态学[3]、社会科学[4]、城市规划[5]等.

空间特征是指空间中不同种类的事物，空间实例是这种类别事物在具体空间位置上的出现.由于空间实例分布的异质性和空间特征实例数量的差异，空间实例通常分布不均，这导致一些同位模式只存在于有限的局部子区域中，于是空间同位模式被分为全局同位模式和区域同位模式.多级同位模式挖掘指挖掘到全局和区域所有的同位模式.

现有的多级同位模式挖掘研究存在诸多问题.多级同位模式挖掘方法往往沿用传统同位模式挖掘中实例间的欧氏距离作为其邻近关系的度量准则，未考虑空间数据分布的网格特性.例如城市网格布局作为城市规划和设计的基本模式，广泛应用于现代城市的管理和规划中；在生态环境中，由于水流和植被分布的相互作用，物种分布呈现网格状分布的现象.空间实例呈现网格分布的现象在现实中非常普遍，只考虑欧氏距离的度量会忽略网格对角线实例间的邻近关系，可能会遗漏某些有潜在价值的同位模式.区域划分的目的是通过合理的划分策略，使划分的区域内部具有相同的模式分布.现有基于点数据聚类的区域划分方法[6-7]存在一系列不足，由于空间数据存在特征实例异质性，只考虑点数据的密度和位置容易忽略特征实例数量的差异，可能导致划分的区域内部缺乏相同的模式分布，使得划分的区域不合理.现有的多级同位模式挖掘方法采用先挖掘全局同位模式，将全局非频繁同位模式识别为候选区域同位模式，并逐一筛选这些候选区域同位模式，以挖掘区域频繁同位模式.这种传统的多级模式挖掘方法需要消耗大量的时间与空间，计算模式的全局参与度.该方法未采用有效的剪枝策略，导致时间复杂度较高.

针对现有的多级同位模式挖掘存在的问题，本文利用网格划分技术重新定义实例之间的邻近关系，利用网格邻近关系和模式参与实例的反单调性提出有效的剪枝策略，使得提出的挖掘算法不仅能够有效地提高挖掘效率，而且挖掘结果更贴合实际应用.在区域划分阶段，采用网格密度峰值聚类的方法，基于网格中2 阶网格空间团定义不同网格的相似性，使得区域划分更合理.因为多级同位模式挖掘方法旨在挖掘出全局和区域频繁的同位模式，但是通过将全局不频繁的模式作为区域候选模式并逐阶筛选，时间复杂度非常高.本文考虑模式的分布情况，提出先挖掘区域同位模式再推导全局同位模式的新颖挖掘框架，时间效率得到了很大的提升.

1 相关工作

Huang 等[8]提出空间同位模式的挖掘，定义参与度来衡量同位模式的频繁程度.基于参与度的反单调特性，提出类Apriori 的挖掘方法，即join-based 算法[8].随后，人们提出各种方法来提高同位模式挖掘算法的效率，例如Partial-join 和joinless 算法[9].由于挖掘同位模式和空间实例的团关系密不可分，人们提出一系列基于团的同位模式挖掘方法，如基于order-cliques 的算法[10]、基于极大团的算法[11].传统的同位模式挖掘方法只着眼于在全局空间中频繁出现的同位模式，忽略了空间数据分布异质性的存在.由于一些模式只在局部子区域内频繁出现，而全局同位模式挖掘方法无法发现这些频繁出现的区域模式，忽略了局部区域信息.区域同位模式挖掘引起了人们的关注，它旨在寻找在局部子区域中频繁存在的同位模式及相应的频繁区域.

区域同位模式的挖掘方法主要可以分为以下2 类.1）基于区域识别的方法，它们通过对空间实例或模式实例进行聚类来识别模式的频繁区域，计算区域内模式的参与度来评价模式的频繁程度.Eick 等[12]将具有最大适配度函数的聚类结果作为挖掘同位模式的区域.Mohan 等[13]提出基于邻域图的方法，发现区域同位模式的频繁区域.Deng 等[14]提出多级挖掘方法，将全局不频繁模式作为候选区域模式，通过Delaunay Triangular 自适应聚类方法识别模式的频繁区域.Liu 等[15]提出基于自然邻居的多级同位模式挖掘方法，建立新的局部自适应邻近关系，但该方法对空间特征的数量比较敏感.Liu 等[16]提出k 近邻中加入道路网格约束和启发式的两阶段方法，通过蒙特卡罗模拟方法评估模式的统计意义，识别每个区域同位模式的频繁区域.2）基于区域划分的方法.这种方法将整个研究区域划分为多个子区域，分别在每个子区域内挖掘同位模式.基于区域划分方法的主要挑战在于找到适当的空间划分方案，目前的研究提出了各种划分区域的方法.Celik 等[17]提出基于四叉树的结构来挖掘频繁的区域同位模式，但需要大量的先验知识.Ding 等[18]使用监督聚类算法，将基于网格的地理空间划分为任意形状的区域.Qian 等[19]提出基于k 近邻的分区方法，用 k=1 初始化原始区域，利用迭代方法合并具有近似距离阈值和一定比例的同类型模式的区域，得到具有相似数据分布的目标区域.Wang等[20]提出挖掘区域同位模式的频繁主义和贝叶斯框架，开发基于概率扩展的启发式方法，寻找任意形状的区域.

本文引用网格密度峰值聚类方法，通过2 阶网格空间团来判断不同网格的相似度进行区域划分.基于数据分布的网格特性提出有效的剪枝策略，设计高效的多级同位模式挖掘算法，解决了传统多级方法时间效率低的问题.本文提出从区域同位模式推导出全局同位模式的新挖掘框架，避免了将区域同位模式误判为全局同位模式的情况，显著减少了计算时间.这些创新使得算法在实际应用中能够更高效地挖掘多级同位模式，得到有意义且可靠的结果.

2 概念与方法

2.1 基本概念

给定空间特征集F={f1,f2,···,fn}，表示整个空间数据集中不同事务类型的集合.空间实例集S=S1∪S2∪···∪Sn中，Si(1 ≤ i ≤ n)为特征为 fi的空间实例集合.为了区别实例，给每个空间实例o 指定实例编号id，于是空间实例一般用三元组＜实例所属特征，实例编号，(x,y)＞表示，x、y 表示该实例在空间中的具体位置坐标.给定距离阈值d，根据距离d 划分网格，而实例的邻域范围为以该实例坐标为中心、边长为2d 的矩形范围.若一个实例位于另一个实例的邻域内，则称2 个实例满足空间邻近关系R.如图1 所示，将满足邻近关系的实例用一条实线连接，实例A1 的邻域为深色虚线矩形，A1 的邻居实例有{B1,B2,C1,D1,D2,D3}.空间特征集F 的子集c 称为空间同位模式，模式c 中特征的个数k 称为模式的阶数.在空间邻近关系R 下，不同特征实例组成的团关系（两两实例之间都满足空间邻近关系R）称为网格空间团；若该团包含模式c 的所有特征且不存在相同的特征实例，则该团被称为k 阶网格空间团，该团的实例集合称为模式的一个行实例.模式的所有行实例组成了模式的表实例.表实例中不重复的实例被称为模式c 的参与实例.如图1 所示为包含4 个空间特征的区域数据示例，右侧列出了一些模式的参与实例.图1 中，包含A1 的网格空间团有{A1,B1,C1,D1}，{A1,B1,C1,D2}，{ A1,B2,C1,D1}，{ A1,B2,C1,D2}，{A1,D3}.

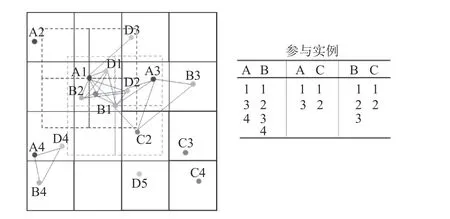
图1 包含4 个空间特征A、B、C、D 的区域数据示例（左图）和一些模式的参与实例(右图)Fig.1 Example of regional data containing four spatial features A,B,C,D (left figure)and some examples of pattern participation instances (right figure)

2.2 区域划分方法

密度峰值聚类[21]是基于密度的聚类算法，能够自动确定聚类中心点和聚类数目，该聚类算法依据以下2 点获取聚类结果.1）簇中心的局部密度较高；2）簇中心离其他簇中心距离较远.密度峰值聚类算法中需要设置一些参数，算法对参数较敏感.本文提出自适应网格密度峰值聚类算法，在簇分配的过程中利用网格中2 阶网格空间团，度量网格之间的相似度.

定义1 网格密度.给定网格g，该网格密度定义为网格内空间实例数量.

式中：Ins (g)为网格内的实例个数.

定义2 网格相对距离.给定网格g，网格相对距离 δg定义为网格密度大于 ρg的网格g'与网格g 的距离的最小值，即

式中：distg′g为网格g 和网格g'的中心点之间的距离，也称为网格g 和网格g'之间的距离.

定义3 中心网格.中心网格gcenter的密度和相对距离经过归一化处理后，密度和距离都大于其阈值.

簇中心满足以下2 个条件：1）簇中心的密度大；2）离其他簇的距离较远.因为密度和距离的单位不一致，对网格密度和相对距离进行归一化处理，max(ρ)、min(ρ)分别为所有网格密度的最大值和最小值，max (δ)和min (δ)分别为所有网格相对距离的最大值和最小值.根据式(3)、(4)计算得到所有网格归一化处理后的密度和相对距离格密度的平均值和标准差，为为所有网格归一化处理后的网所有网格归一化处理后的网格相对距离的平均值和标准差.标准差的引入使得算法更具有鲁棒性[22]，在数据分析中平均值加标准差是常用的标准化指标，能够提供有关数据点分布情况的信息，辅助异常值的检测.这里的异常值指局部密度和相对距离都异常大的数值，符合作为簇中心的条件，所以将归一化处理后的结果计算平均值加标准差并作为阈值：

区域划分的目的是通过合理的划分策略，使划分的区域内存在尽可能相同的区域模式.为了使具有相同模式的区域尽可能地聚集在一起，在聚类过程中需要进一步考虑网格内部的模式.在同位模式挖掘中，2 阶网格空间团探究的是不同空间位置上对象的属性之间的相关性，通过分析2 阶网格空间团可以预测出更高阶模式的潜在联系，所以考虑利用2 阶网格空间团度量不同网格的相似度.

定义4 网格相似度.给定中心网格gcenter和待分配的网格g，2 个网格的相似度定义如下：

gcenter和g 的2 阶模式并集为c={c1，···，ci，···，cn}，其中n 为2 阶模式并集中的种类个数；gcenter(ci)、g(ci)分别为中心网格gcenter和网格g 内包含的2 阶模式 ci的网格空间团的数量.0 ≤Sg(gcenter,g)≤1.0，相似度越接近于1，表示待分配的网格与中心网格内部的2 阶模式种类趋于相同且数量相近，则2 个网格内部的同位模式相似度越高.如图2（网格内的实例都存在邻近关系，证明见引理6）所示，网格2 中包含的2 阶模式有{A,C}、{A,D}、{C,D}，且模式网格空间团个数分别为9、6、6.网格4 中的2 阶模式有{A,C}、{A,D}、{C,D}、{A,E}、{C,E}、{D,E}，模式的网格空间团个数分别为4、4、4、2、2、2.这2 个网格的相似度

图2 说明网格相似度度量的用例Fig.2 Examples for illustrating grid similarity measure

算法1(AG-DPC)将整个研究区域S 划分成d×d 的网格（行1）.根据定义1 计算每个网格密度并将其存储到集合 ρ中（行2），在获得每个网格的密度后，根据定义2 计算网格的相对距离（行3）.根据定义3，找到簇中心，即中心网格（行4～7）.对非中心网格进行分配，将非中心网格分配到距离较近且相似度较高的中心网格（行8～10），得到划分的 区域（行11）.

2.3 多级同位模式挖掘

多级同位模式挖掘旨在挖掘全局和局部区域2 个不同层次中频繁出现的同位模式.传统的多级同位模式挖掘算法未考虑数据的网格特性，将全局不频繁的模式作为区域候选模式，进行一一筛选，在挖掘多级同位模式时需要消耗大量时间和空间搜索和存储模式的表实例，而生成表实例对计算模式的参与度是非必要的[23]，如图3(a)所示为传统的多级模式挖掘框架.本文提出从区域同位模式推出全局模式的新框架（见图3(b)），采用搜索参与实例的策略，结合网格特性和参与实例的反单调性提出剪枝策略，以有效挖掘多级同位模式.

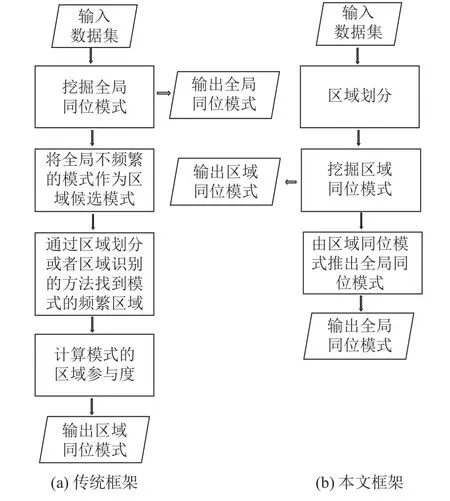
图3 多级同位模式挖掘框架上的对比Fig.3 Comparison of multi-level co-location pattern mining framework

定义5 区域参与度PI、区域参与率PR.给定模式c 及其所在区域r，该模式c 中特征fi在区域r 的区域参与率 PR(r,c,fi)和模式c 的区域参与度 PI(r,c)表示为

式中：R(r,fi)为区域r 中特征 fi的实例集合，Obj(r,c,fi)为fi在区域r 中模式c 的参与实例集.模式c 在区域r 的参与度 PI(r,c)定义为模式c 的所有空间特征中参与率的最小值.

定义6 区域同位模式RCP.给定模式c 及其所在区域r，若该模式c 在区域r 内的参与度PI(r,c)≥频繁度阈值 θ，则称模式c 在区域r 内是区域频繁同位模式，简称区域同位模式.

如图1 所示，在区域中，假设区域频繁度阈值为0.4，PI(r,{B,C})=1/2 ＞ 0.4，则模式{B,C}为区域同位模式.

定义7 全局同位模式GCP.给定模式c 和面积占比阈值 ε，若该模式所在的频繁区域面积与全局面积的占比A(c)大于 ε，则称该模式c 为全局同位模式.

式中：ri为模式c 的某个频繁区域，Rc为模式c 的频繁区域集，S(ri)为区域 ri的区域面积，global-Area 为整个研究空间的面积，0≤A(c)≤1.0.全局模式指在整个研究空间中频繁出现的模式.本文的全局模式考虑了分布情况，可以避免将不小于全局频繁度阈值的区域同位模式误判为全局同位模式的情况.

引理1 区域模式在区域内满足先验性原理.在区域r 中，若区域模式是区域频繁的，则其子模式也是区域频繁的；若区域模式不是区域频繁的，则其超模式也是区域不频繁的.

证明：若模式c 在区域r 中频繁即满足PI(r,c)≥θ；在区域内参与度满足向下闭合性[8]，c 的子集 c′，c′⊂c，则不等式 PI(r,c′)≥PI(r,c)≥θ恒成立，即c 的子集一定是区域频繁的.同理可得，若区域模式不是区域频繁的，则其超模式也一定不是区域频繁的.

引理2 全局模式满足先验性原理.若全局模式是频繁的，则其子模式也是频繁的；若全局模式不是频繁的，则其超模式也是非频繁模式.

证明：由于本文的全局模式是由区域同位模式推出的，区域同位模式在其频繁区域中满足先验性原理，一个模式在区域中是频繁的，那么其子模式也是区域频繁的(引理1).子模式subc 所占的区域面积一定大于等于该模式c 的区域面积，即整个研究空间面积globalArea 是常数值，可以得到

即ε ≤A(c)≤A(subc)，所以若全局模式是频繁的，则其子模式也是频繁的.因为一个模式在区域中是非频繁的，其超模式也是非频繁的，所以超模式supc 所占的区域面积一定小于该模式c 的区域面积.同理可得若全局模式不是频繁的，则其超模式是非频繁模式.

当计算区域模式的参与度时，不需要再花费大量时间和空间存储模式的表实例，只需要存储表实例中不重复的实例即参与实例.在区域内从低阶向高阶挖掘区域同位模式，需要进一步考虑高阶的候选参与模式，以减小搜索空间.

定义8 候选参与实例集.在区域r 中，特征f 在k(k ＞2)阶同位模式c 中的候选参与实例集是f 在模式c 的所有包含f 的k-1 阶子模式中的参与实例集的交集，表示为

引理3在 CObj(r,c,f)中搜索特征f在模式c 中的参与实例集是完备的，即

证明：若 Obj(r,c′,f)已知，当挖掘区域同位模式时，c′⊂c，对于f 在c 中任一参与实例o∈Obj(r,c′,f)，选取c 的某条行实例RI 包含o，取RI 中包含 c′的所有特征的行实例 RI′，则 RI′中一定包含实例o，即Obj(r,c,f)⊆Obj(r,c′,f).若Obj(r,c′,f)未知，则用区域特征集R(r,f)代替，R(r,f)一定包含特征f 在区域模式c 中的所有参与实例，即Obj(r,c,f)⊆R(r,f)，所以O bj(r,c,f)⊆CObj(r,c,f).

引理4在区域r 中，对于区域同位模式c 及其特征f(f∈c)，特征f在区域同位模式的参与度上界表示为RUPR(r,c,f)=||CObj(r,c,f)||/|R(r,f)|.若RUPR(r,c,f)＜θ，则该模式一定不是区域频繁同位模式.

证明：根据引理3可知，Obj(r,c,f)⊆CObj(r,c,f)，则||Obj(r,c,f)||≤||CObj(r,c,f)||，因此PR(r,c,f)=|Obj(r,c,f)|/|R(r,f)|≤||CObj(r,c,f)||/| R(r,f)|＜θ，PI(r,c)＜θ.

基于参与度上界的剪枝策略.根据引理4 可知，若模式c 中存在某一特征f 的参与度上界RUPR(r,c,f)＜θ，则该模式一定不是区域同位模式.在得到模式的候选参与实例集后，可以直接计算区域模式的参与度上界.在区域内，若该模式的参与度上界未达到频繁度阈值，则提前将该模式进行剪枝操作，不需要再搜索该模式的参与实例.

引理5包含模式c 的参与实例的网格为c 中所有特征f(f∈c)的候选参与实例所在网格的交集网格.

证明：由引理3 可得，模式c 的参与实例一定存在于模式c 的候选参与实例中，可以得到模式c 的参与实例所在的网格一定包含于候选模式参与实例所在的网格范围内.如果要找到包含模式c 的参与实例的网格，那么这些网格一定包含在所有特征的候选参与实例所在的网格的交集中.如图4 所示为区域r 的实例分布，(gridX,gridY)为网格的编号.根据定义8 列出模式{A,B,C}的候选参与实例集，显示了候选参与实例所在的网格标号，可以看出网格(1,2)是模式{A,B,C}的所有特征所在网格的交集，即网格(1,2)内存在{A,B,C}的网格空间团.

图4 候选参与实例的示例Fig.4 Examplesofcandidateparticipatinginstances

引理6若某一网格内包含模式c 的所有特征，则这些特征实例o(o.f∈c)都为模式c 的参与实例.

证明：由邻近关系的定义可知，实例的邻域范围是以该实例坐标为中心、边长为2d 的矩形，则实例的邻域范围一定包括实例所在的网格.网格内的所有实例都存在邻近关系，即满足团关系，所以只要网格内包含模式c 的所有特征，则这些特征实例o(o.f∈c)一定为模式c 的参与实例.如图4 中A1 所在的网格(1,2)，都存在邻近关系，则在网格(1,2)内，特征B 在模式c={A,B,C,D}中的参与实例为Obj(r,c,B)={B1,B2}.

引理7在区域r 内，若模式c 在网格内的区域参与度为 PIintra(r,c)，则称其为区域参与度下界.因为真实的区域参与度一定大于等于 PIintra(r,c)，若区域参与度下界达到频繁度阈值，则模式c 一定是区域频繁的.

证明：区域模式c 存在以下2 种情况.1）模式的网格团关系完全存在于网格内，如图4 的团关系(A1,B2,C1).2）模式的网格团关系存在于网格间，如图4 的(A3,B1,C2).模式的区域参与度由2 部分组成：PI(r,c)=PIintra(r,c)+PIinter(r,c).若模式c 在网格内的区域参与度已经达到频繁度阈值，即 PIintra(r,c)≥θ，则PI(r,c)=PIintra(r,c)+PIinter(r,c)≥θ，即模式一定是频繁的.

基于参与度下界的剪枝策略.根据引理5 找到区域模式c 完全存在于网格内的情况，可以进一步缩小搜索范围.根据引理6 可知，网格内部的特征实例o (o.f∈c)可以直接被认为是参与实例，无须再搜索区域模式的团关系.根据引理7 计算模式的区域参与度下界，若模式的区域参与度下界不小于频繁度阈值，则该模式一定是区域频繁的，不需要搜索出所有的参与实例.

3 算法与分析

3.1 算法描述

提出的算法利用2.2 节中网格密度峰值聚类的方法进行区域划分，开展多级同位模式挖掘.采用先挖掘区域频繁模式再推导出全局频繁模式的 多级同位模式挖掘框架，具体算法如下.

在算法2(S-ML)中，根据算法1 的网格密度峰值聚类获得划分区域(行1).在区域划分的基础上，对每个区域进行区域同位模式挖掘（行3～12）.根据区域内上一阶的频繁区域模式生成候选模式（行6），验证每个候选模式是否在区域内频繁（行7～9，具体见算法3）.与传统的多级同位模式挖掘不同，算法2 从区域同位模式推出全局模式（行10、11），该全局模式不需要计算参与度，因此不需要存储全局的参与实例集，节省了空间消耗，只需要计算模式c 的区域面积与全局空间面积的比值.若模式c 在之前区域中未被判定为频繁全局模式，则计算模式当前频繁区域的面积之和与全局面积的比值 A′(c).若A′(c)≥ε（A′(c)≥A(c)），则认为该模式为全局模式.

算法3 (IsRegionalCo-location)描述了如何判断模式c 在区域r 中的频繁性.在区域中挖掘同位模式先通过模式的参与度上界和下界进行剪枝，根据定义8 得到模式中特征的候选参与实例，根据引理4 计算得到参与度上界（行2）.若存在某一特征的区域参与度上界未达到频繁度阈值，则说明该模式在区域r 中不是频繁的，直接返回False（行3）；否则根据引理7 计算模式的区域参与度下界，记录网格内模式的参与实例（行4）.若模式的区域参与度下界达到频繁度阈值，直接返回True（行5、6）；否则在区域中搜索模式的所有参与实例，计算参与度，判断频繁性（行7～12），具体见算法4.

算法4(Search)描述了如何在区域r 中搜索c 的参与实例，由引理3 可知，在区域模式的候选参与实例集 CObj(r,c,f)中搜索参与实例是完备的，所以只须在候选参与实例集中验证实例是否为区域模式的参与实例（行1、2）.根据引理7 可知，当计算模式的区域参与度下界时，已经得到了区域内包含模式c 的所有网格，并记录了网格内的参与实例.对于网格内的参与实例，直接返回true（行3、4）.若实例o 不是网格内参与实例，则将搜索空间扩展到实例o 所在的网格o.g 及其周围8 个邻近网格（实例o 的邻域范围）.若该搜索空间不包含c 的所有特征实例，则实例o 一定不是c 的区域参与实例（行5～7）；若该搜索空间包含c 的所有特征实例，则采用回溯法BracktrackingSreaching(S,X,i,flag)进行搜索.回溯搜索首先初始化解空间S 和数组X，其中X[i]用于记录当前解空间的第i 个特征f 的实例，flag 标记是否找到模式c 的网格空间团包含实例o，搜索实例集为o 的邻域中除o.f 以外的特征实例Oss {f,o'.f}（o'.f≠o.f）(行9).初始搜索空间为实例o 的邻域范围，每往X 中加入一个实例o'（加入的实例需要满足在搜索空间内且与当前X 中的实例都存在邻近关系），则将搜索空间缩小为实例o 与实例o'的邻域范围的交集.若X 中没有实例可加入且X 不满足解空间，则进行回溯，同时搜索空间也还原至上一级；以此类推直至找到满足条件的解空间或者搜索完Oss 的可行路径（行10）.若最后返回的S 不只包含实例o，则说明找到了包含实例o 的网格 空间团，记录相应的参与实例（行11～13）.

3.2 算法时间复杂度的分析

分析算法AG-DPC 和S-ML 的时间复杂度，以下均假设数据集拥有y 个特征、m 个网格、z 个区域.

AG-DPC：提出的基于网格的密度峰值聚类算法将数据分布空间划分为m 个网格，假设中心网格数量为g 个，每个网格内的特征数量为x 个(x＜＜y)，则网格内的2 阶网格团的种类有种，AG-DPC 的时间复杂度为O (g (m-g)).

S-ML：算法S-ML 采用分区后逐阶挖掘区域同位模式，该算法仅挖掘区域同位模式，并由区域模式推导出全局模式，不需要计算模式的全局参与度.最坏情况下区域内的特征数有y 个，区域每个特征的实例数最多为n.在每个区域中从2 阶开始逐阶进行区域同位模式挖掘，最坏情况下模式的最高阶数为y (一般情况下，由于邻近关系和频繁度阈值的约束，模式的最高阶数远小于y).假设每次迭代中搜索的候选区域模式个数为 |RCP|.每个模式都需要判断其区域频繁性和全局频繁性.当判断区域频繁性时，最坏情况下通过模式的上、下界无法判断频繁性，且模式的网格空间团都存在于网格间，因此需要通过调用BracktrackingSreaching(S,X,i,flag)搜索模式的参与实例.每次调用BracktrackingSreaching(S,X,i,flag)的时间复杂度为O(knk)，其中k 为当前阶数，则在每个区域内挖掘区域模式的时间复杂度为

在推出全局模式时，仅需要考虑模式所在区域面积与全局面积的比值.在最坏情况下，每个模式都在其最后一个频繁区域中判断出全局频繁性，即在每个区域中的每个模式都需要计算A(c)，则推导出全局同位模式的时间复杂度为O (zy×|RCP|).综上所述，S-M L 总的时间复杂度为O (zny+1|RCP|)+O (zy|RCP|).

4 实验结果与分析

使用真实和合成数据集，评估所提出的多级同位模式挖掘算法的有效性、效率和可扩展性.实验中的算法均由C++实现的.硬件环境为Intel Core i7 3.70 GHz CPU、16 GB RAM.运行环境为Microsoft Windows 10、Clion2021.

4.1 实验数据集

采取2 个真实数据集对算法展开测试：1）深圳POI 数据集，包含13 个空间特征、71 606 个空间实例，数据分布形状偏向于簇状分布；2）高黎贡山的植物数据分布集，包含25 个空间特征，13348个空间实例，数据偏向于均匀分布.2 个真实数据集的实例分布及其分区结果如图5 所示.采用文献[7]的数据合成方法生成合成数据集，实验模拟数据在10 000×10 000 的范围内生成.

图5 真实数据集分布及其分区结果Fig.5 Distribution of real datasets and their partition results

4.2 真实数据集上的实验分析

4.2.1 网格空间团的网格相似性度量方法的有效性 区域划分的目的是通过合理的划分策略使划分的区域内存在尽可能相同的区域模式.为了验证提出的利用2 阶网格空间团获取目标区域的效果，定义区域划分的评估指数EI.

式中：R1、R2为2 个相邻的区域；n 为区域个数，SR(R1,R2)为2 个区域内的区域同位模式之间的相似度，RC1i、RC2i分别为区域R1、R2的i 阶同位模式，J 为Jaccard 指数.EI 反映了整体空间的区域划分的合理性，且0 ≤ EI ≤1.0.EI 越大说明相邻区域之间挖掘到的同位模式越不相同，EI 越小说明相邻区域之间挖掘到的同位模式越相同.相邻的不同区域之间应该具有明显的分割特征，不应该具有相似度较高的挖掘结果，间接反映出区域划分的不合理性.

与基于区域划分的方法FDPC-RCPM[6]方法及不采用网格相似度的区域划分方法进行对比.将频繁度阈值设置为0.4.如表1 所示为这些方法在真实数据集上的EI 值.可以看出，利用2 阶网格空间团划分区域的合理性最高.FDPC-RCPM 方法采用模糊密度峰值聚类的方法划分区域，在划分过程中仅考虑实例数据点的密度和距离，未考虑同位模式，导致相邻的区域中存在很多相同的同位模式，即划分的区域存在不合理性.为了对比网格空间团的网格相似性度量方法的有效性，对网格相似性度量进行消融实验，设计不采用网格相似度的区域划分方法S-ML-2.S-ML-2 存在与FDPC-RCPM[6]方法同样的问题.

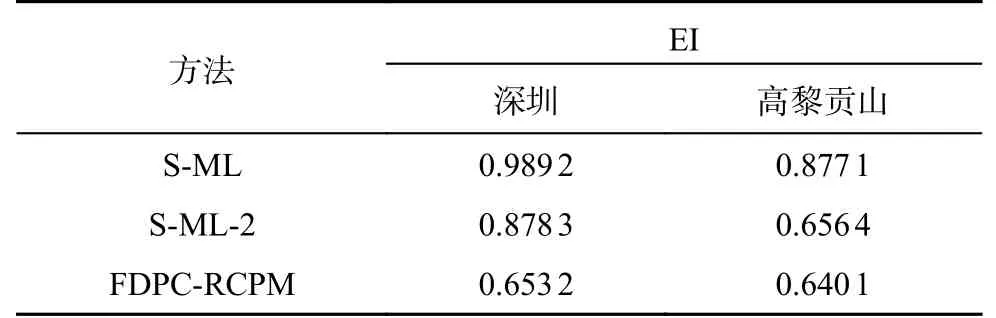
表1 不同方法的EI 值Tab.1 EI values for different methods

4.2.2 挖掘结果的有效性 深圳POI 数据集中特征A 和特征B 的实例分布情况如图6(a)所示，可以看出模式{A,B}分布的范围较广.ML 方法[14]是传统的多级同位模式挖掘方法，采用模式聚类的方法获取频繁区域.图6(c)中被框出的区域表示在ML 方法下挖掘到的模式{A,B}的频繁区域.可以看出，仅找到了模式{A,B}的部分区域.本文的挖掘结果（见图6(b)）更加符合实例的分布情况，挖掘的区域更全面.

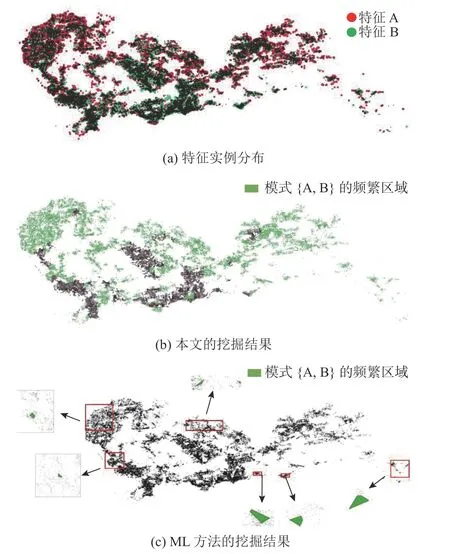
图6 挖掘到的区域模式频繁区域的比较Fig.6 Comparison of mined prevalent regions of regional co-location patterns

在传统的多级挖掘方法中，全局同位模式是满足全局频繁度阈值的模式，即表示该模式在整个研究空间中频繁出现的模式；本文的全局模式不从参与度的角度考虑，从区域同位模式考虑，频繁的区域同位模式出现在多个区域，且这些区域的面积占整个研究区域面积的比值达到给定阈值时，认为该模式为全局频繁模式.当挖掘全局模式时，ML 方法仅考虑模式的全局参与度，忽略了模式的分布情况，会造成仅分布在局部小区域的模式被误判为全局模式，如图7 所示，深色部分表示该模式存在的区域，这些区域面积占比很小，不满足模式在全局范围内频繁共现.本文挖掘的全局模式在区域模式的基础上考虑了模式的分布情况，从图8 可以看出，模式在全局范围内频繁出现（浅色为模式分布的区域）.

图7 利用ML 方法识别的全局模式的分布Fig.7 Distribution of global patterns identified by ML

图8 利用提出方法识别的全局模式的分布Fig.8 Distribution of global patterns identified by proposed method

通过对比挖掘到的区域模式和全局模式，可知提出的挖掘方法的结果更加合理.

4.2.3 挖掘效率 为了对比本文方法与其他多级同位模式挖掘方法的执行效率，对比了3 个传统多级同位模式挖掘方法(ML[14]、NN[15]、QGFR[24])和2 个仅挖掘区域同位模式的方法(KNNG[19]、FDPC-RCPM[6]).将深圳POI 数据的邻近阈值设置为100，高黎贡山的邻近阈值设置为1 500 (深圳POI 属于城市建筑数据，实例之间的距离较近；高黎贡山属于植被数据，实例之间的距离较远.在考虑数据集内实例的平均距离后分别设置了相对较合理的距离阈值).其中采用k 近邻生成邻近关系的方法（KNNG、FDPC-RCPM），将输入距离阈值的平均邻居个数作为k 值.NN 方法是基于自然邻居挖掘多级同位模式，建立新的局部自适应邻近关系，对特征数量极其敏感.QGFR 方法使用最小正交包围矩形作为模式的区域,但得到的区域形状固定为正交矩形,且即使在带有剪枝策略的情况下,算法的时间复杂度仍极高.在本实验中仅限于比较方法的时间效率，无法在24 h 内获取到NN 方法和QGFR 方法的实验结果.

如图9 所示为在不同的频繁度阈值P 下多个方法的运行时间T.可以看出，在不同的频繁度阈值下，本文方法的时间效率最优.ML 方法将全局不频繁的模式全部作为区域候选模式.随着频繁度阈值的增加，全局同位模式数量减少导致区域候选模式数量增加，ML 方法需要对每个候选区域模式计算区域参与度，导致消耗大量的运行时间.KNNG 方法需要花费大量的时间验证相似的模式，获取目标区域，计算参与度.FDPC-RCPM 方法在每个区域中采用原始的join-less 方法进行挖掘,并未优化算法效率.本文提出的方法采用参与度的上下界进行有效剪枝，只需要对不能剪枝的模式计算区域频繁度，时间效率有了很大的提升，甚至优于仅挖掘区域同位模式方法的时间效率.

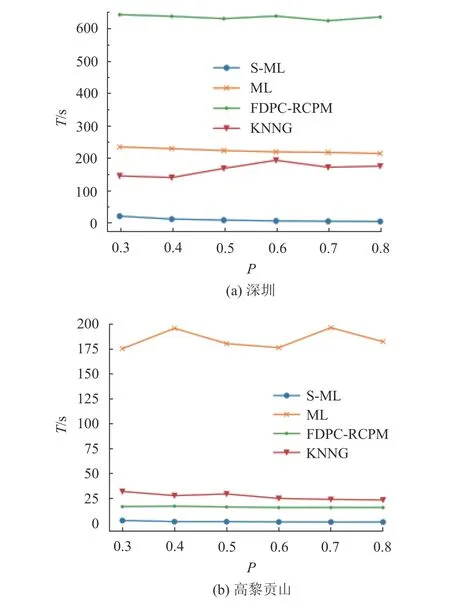
图9 在不同频繁度阈值下的运行时间对比Fig.9 Comparison of running time under different prevalent thresholds

本文方法是新颖的多级同位模式挖掘方法，将其挖掘结果与传统多级方法ML 进行对比.随着频繁度阈值的增大，利用这2 个方法挖掘到的模式数量递减.本文所挖掘到的区域模式数量多于ML 方法挖掘到的模式数量，如图10 所示.图中，N 为模式数量.这是因为考虑了实例之间的网格特性，且邻近关系包括对角线可达性，相比于ML 方法中的邻近关系，本文的邻近关系更丰富，可以捕捉到更多有潜在价值的模式.此外，本文避免了将区域模式误判为全局模式，而ML 方法存在误判的情况，这导致ML方法挖掘到的区域模式数量较少.

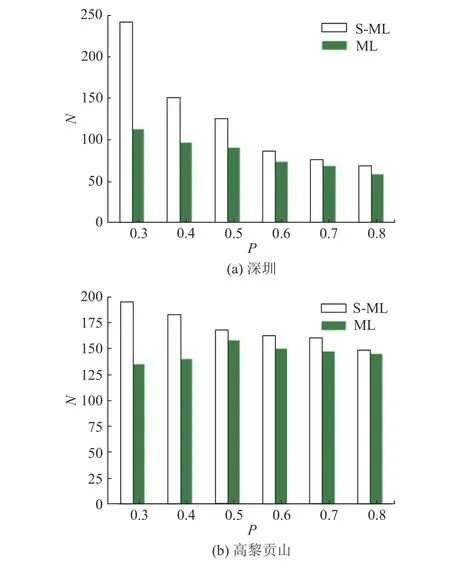
图10 在不同频繁度阈值下的区域模式数量对比Fig.10 Comparison of number of regional patterns under different prevalent thresholds

4.2.4 剪枝效率 图11 中，Nc为候选模式的数量，Np为剪枝模式的数量，R 为剪枝率.如图11 所示，随着频繁度的增加，剪枝率逐渐上升.由于本文方法利用网格特性和模式参与实例的反单调性，对候选模式进行剪枝.随着频繁度的增加，提前被剪枝的模式数量也增加，剪枝率一直上升.在高黎贡山数据集上，当频繁度为0.8 时，剪枝率可以达到78%.通过实验验证了提出的S-ML 算法在2 个真实数据集上剪枝策略的有效性.

图11 S-ML 算法的剪枝率Fig.11 Pruning rate of S-ML algorithm

4.3 合成数据集上算法的可扩展性分析

根据文献[7]的数据生成方法，合成7 个数据集，实例个数为10 000～60 000，将频繁度阈值设置为0.4.实验结果如图12(a)所示，Ni为实例的数量，Nf为空间特征的数量，随着实例数量的增加，所有算法的耗时均呈上升趋势.其中FDPCRCPM 方法在实例数为10 000 时时间消耗已达到587 s，在实例数超过20 000 后运行时间超过600 s.与其他算法相比，提出的算法在效率上表现显著更高，并一直保持较高的运行效率.

图12 合成数据集上的实验对比Fig.12 Experimental contrasts on synthetic datasets

空间特征数量对同位模式的阶数有着较大的影响.为了研究特征数量对算法运行效率的影响，合成了5 个不同特征数量的数据集，实例数量为10 000.实验结果如图12(b)所示，S-ML 算法的运行效率较高.

综上所述，提出的算法具有良好的时间效率，在处理大规模实例数量时具有更好的可扩展性.

5 结 语

本文提出基于网格空间团的多级同位模式挖掘方法.传统的邻近关系定义通常只考虑空间实例之间的欧氏距离，忽略了真实数据普遍的网格化分布.为了弥补这一不足，采用网格邻近关系来替代传统的基于距离的邻近关系.在区域划分阶段，针对点聚类划分区域方法的不足，提出优化的网格密度峰值聚类方法，在聚类的基础上进一步考虑网格内模式的相似情况.在模式挖掘阶段，提出从区域同位模式推导出全局同位模式的挖掘新框架，设计带有剪枝策略的多级同位模式挖掘算法.该算法不仅避免了将区域同位模式误判为全局同位模式的情况，还减少了计算全局参与度的时间，显著提升了时间效率.本文的全局模式考虑了模式的分布情况，使得结果更加准确.通过实验验证了挖掘结果的有效性和合理性，在真实和合成数据集上进行了广泛的实验，验证了本文算法的高效性和可扩展性.