基于大规模多目标优化的跳频序列设计方法

张毅恒 刘以安 宋海凌

摘 要：

针对跳频序列设计中存在的规模小和难以兼顾多指标的问题，提出一种基于大规模多目标优化的跳频序列设计方法。首先，综合考虑跳频序列的多项性能指标，建立跳频序列多目标优化模型；然后，引入大规模多目标优化方法，并提出决策变量洗牌策略和反向差分进化，通过重新分配决策变量位置以形成具有多样性的非支配集，并通过使反向个体参与差分进化来为后续进化持续提供有效的方向；最后，通过提出算法对模型进行优化得到跳频序列集。实验结果表明，所提方法相较于其他多目标优化方法具有更强的寻优能力，得到跳频序列集的性能指标具有明显优势；所提方法在不同干扰环境中相较于其他方法具有更低的误码率，验证了提出方法的有效性和优越性。

关键词：抗干扰；跳频序列；大规模多目标优化；洗牌策略；反向学习

中图分类号：TP391   文献标志码：A    文章编号：1001-3695（2024）03-036-0887-07doi： 10.19734/j.issn.1001-3695.2023.08.0336

Frequency-hopping sequence design method based on large-scale multi-objective optimization

Zhang Yiheng1， Liu Yian1， Song Hailing2

（1.School of Artificial Intelligence & Computer Science， Jiangnan University， Wuxi Jiangsu 214122， China; 2. Naval Research Institute， Beijing 100161， China）

Abstract：

Aiming at the problem of small scale and difficulty in taking into account multiple indexes in the design of frequency-hopping sequences， this paper proposed a frequency-hopping sequence design method based on large-scale multi-objective optimization. Firstly， considering the multiple performance indexes of frequency-hopping sequence， this paper established a multi-objective optimization model of frequency-hopping sequence. Then， this paper introduced a large-scale multi-objective optimization algorithm， and proposed the decision variable shuffling strategy and the opposition-based differential evolution， which could form a diverse non-dominated set by redistributing the position of decision variables and provide an effective direction for subsequent evolution by enabling reverse individuals to participate in differential evolution and provides an effective direction for subsequent evolution. Finally， this method used the proposed algorithm to optimize the model to obtain a frequency-hopping sequence set. The experimental results show that the proposed algorithm has stronger optimization ability than other multi-objective optimization algorithms， and the performance indexes of the frequency-hopping sequence set has obvious advantages. In different interference environments， the proposed design method has lower bit error rate than other methods， which verifies the effectiveness and superiority of the proposed method. Key words：anti-jamming; frequency-hopping sequence（FHS）; large-scale multi-objective optimization; shuffle strategy; opposition-based learning

0 引言

跳頻通信技术通过跳频序列控制载波频率跳变以实现频谱的扩展，具有抗干扰能力强、隐蔽性好、可实现码分多址等优点，已成为各领域通信中应用最为广泛的一种通信技术［1～3］。

跳频序列（FHS）的设计问题是跳频通信技術的核心。优秀的跳频序列能够满足多项性能指标，通常具有较低的频率碰撞、尽可能长的周期、在工作带宽内均匀分布以及良好的复杂度。针对频率碰撞，研究人员基于采样序列［4］、交错技术［5］、分圆定理［6］、循环码［7］等方法，设计了达到最低碰撞界的跳频序列或跳频序列族，目前该类设计方法已相对成熟，具有完备的理论体系。此外，研究人员还基于混沌理论如四维混沌系统［8］、混沌映射［9］等方法设计具有高随机性的跳频序列，以提高跳频序列的复杂度，增强通信的保密性。随着优化算法的发展，研究人员在设计跳频序列时开始对混沌系统和优化模型进行优化。文献［10］利用粒子群优化算法对三维混沌系统的参数进行优化，优化目标仅考虑复杂度，本质是单目标优化。文献［11，12］都对多个目标进行优化，并利用加权法将多目标函数转换为单目标函数，再使用优化算法对目标函数进行优化，得到跳频序列。

通过分析现有设计方法，目前对于跳频序列的设计研究主要存在以下几点问题。首先，以最低频率碰撞为目标的设计方法考虑的跳频序列指标单一，这使得跳频序列不能适应各类复杂的干扰环境，较易被第三方截获利用；其次，基于混沌序列设计的跳频序列，受制于计算平台的运算精度难以无限提升，在有限精度条件下，系统混沌特性退化，导致序列出现短周期现象，限制了混沌序列的不确定性。最后，在考虑优化算法的跳频序列设计中，仅利用加权法将多目标函数转换为单目标函数，并未考虑指标之间的影响，且未考虑跳频序列长度增加时，优化算法易陷入局部最优和难以收敛的问题。

综上所述，跳频序列具有多项性能指标，为提高跳频通信系统在不同干扰环境中的抗干扰能力，需要兼顾不同指标，因此可通过多目标优化方法来对跳频序列的多项指标进行同时优化。此外，在实际的跳频通信系统中，尤其是军用跳频系统中，跳频序列的长度必须尽可能长，以避免第三方通过序列预测进行破译。这使得多目标优化中个体的决策变量维度激增，因此跳频序列的设计问题必须作为大规模多目标优化问题（large-scale multi-objective optimization problem， LSMOP）来处理。对此，本文提出基于大规模多目标优化的跳频序列设计方法。首先，以跳频序列的最大汉明自相关、复杂度、均匀性为目标函数，建立跳频序列多目标优化模型。之后，针对跳频序列性能指标受决策变量顺序影响的特点，引入基于增强搜索的大规模多目标优化算法，并提出决策变量洗牌策略与反向差分进化，以提高优化过程中非支配集的多样性和算法的寻优能力。实验证明，通过本文方法设计的跳频序列具有更好的性能指标，并在各类干扰环境中具有更低的误码率。

1 跳频通信系统模型

跳频通信技术的原理是将窄带信号的载波频率在跳频序列控制下进行离散跳变，从而达到扩频的效果，降低通信信号被侦察和干扰的概率。

设数据流为双极性信号a（t），取值为±1，跳频序列控制下的瞬时频率为f（t），随时间变化。

2.4 基于大规模多目标优化的跳频序列多目标优化算法

为了延长序列周期，减少跳频序列被预测的可能，序列的长度应尽可能长，这使得跳频序列多目标优化模型中决策空间呈现大规模的特点，因此该优化问题必须作为LSMOP来处理。

LSMOP的主要难题表现在两个方面［18，19］。对目标空间而言，由于目标函数之间的冲突，导致难以存在单个最优解，只能期望获得一组收敛性好且分布均匀的Pareto最优解。对决策空间而言，随着决策变量的线性增加，决策空间规模呈指数级扩张，容易产生“维度灾难”问题。因此，常规多目标优化算法的优化性能在求解LSMOP时会快速下降。目前为止，针对LSMOP，研究者提出了一些大规模多目标进化算法（large-scale multi-objectuve evolutianary algorithm， LSMOEA）。这些算法大致可分为三类：a）将决策变量分组，进而将LSMOP转换为较小规模的MOP［20，21］；b）采用问题转换的方法将LSMOP转换为低维问题［22］；c）基于增强搜索［23，24］，通过设计新的进化算子和概率模型，来对决策变量进行高效的整体优化。

在跳频序列多目标优化模型中，优化目标不止取决于决策变量的取值，还与决策变量的顺序直接相关，因此决策变量之间的关系相较于普通问题更为复杂。若采用决策变量分组的方法，交互变量易被分至不同组，且分组效果易不稳定，子问题仍可能是LSMOP。若采用问题转换的方法，尽管可以缩小搜索范围，但容易丢失全局最优解，且较难选取合适的转换函数。

本文引入Zhang等人［25］提出的LSMaODE算法，该算法基于增强搜索的思想，能够对大规模决策变量进行整体优化，并且不会破坏决策变量之间的顺序关系，更适用于跳频序列多目标优化。首先，将种群分为两个子种群，对其中10%的个体采用随机坐标下降（randomized coordinate descent，RCD），以独立开发和探索决策变量，并且保证决策空间的多样性以避免过早收敛到局部最优。其次，剩余90%的个体根据非支配引导随机插值（nondominated guided random interpolation，NGRI）进行变异，随机选择三个非支配解，并在其中插值生成新个体，从而在引导子种群快速收敛到非支配解的同时，保持个体良好的分布。

此外，针对跳频序列在多目标优化过程中的特点，提出决策变量洗牌策略与反向差分进化，并与LSMaODE相结合，提出针对跳频序列多目标优化模型的LSMaODE-FHS算法，以提高种群中个体跳出局部最优的能力和Pareto最优解集的多样性。

2.4.1 RCD

设P（i）t是第t代群体Pt中的第i个个体，x（i）k是个体P（i）t的第k个决策变量。对于每个个体，对其决策变量独立进行变异和选择。令NewP（i）t=P（i）t，如果随机数大于0.1，则通过一个标准差为（UBk－LBk）/10的高斯随机数来生成突变算子，对决策变量进行变异，得到新个体的决策变量NewP（i）t.xk。否则，从种群中随机选择三个候选个体P（r1）t、P（r2）t和P（r3）t，通过差分进化算子进行变异，描述如下：

2.6 时间复杂度分析

RCD的时间复杂度为O（N2P2）， NGRI的时间复杂度为O（MP2）。由于N>>M，则O（N2P2）>>O（MP2），所以LSMaODE的时间复杂度可记为O（N2P2）。

决策变量洗牌策略的时间复杂度为O（NP），在改进RCD后，时间复杂度保持不变；反向差分进化无须计算目标函数，因此时间复杂度为O（NP），在改进NGRI后，时间复杂度为O（NP+MP2）。由于O（N2P2）>>O（NP+MP2），所以改进后算法的时间复杂度仍可记为O（N2P2）。

3 实验分析

3.1 优化性能分析

本实验中，采用超体积指标HV（hypervolume）指标［29］来评估多目标优化算法的性能。HV指标能够根据非支配集个体与参考点在目标空间中所围成的超立方体体积，对解集的收敛性和多样性进行评价。HV越大，解集的收敛性和多样性越好。

令种群规模为100，迭代次数为200，LB=3，UB=35，跳频序列长度为N，频点数q=32。指标计算中，散布熵参数取m=2、c=4、d=1。

对比算法选用LMEA［20］、LMOCSO［24］、IM-MOEA/D［30］、NAS-MOEA［31］、LSMaODE和LSMaODE-FHS，在跳频序列多目标优化模型上的针对不同跳频序列长度各自重复实验30次，计算HV指标，并将所得解集转换为跳频序列集，计算最大汉明自相关、散布熵和均匀性的平均值，如表1～4所示。

LMEA、LMOCSO在各测试中的性能表现明显差于其他算法，说明聚类分组、竞争粒子群优化的进化方式较难处理跳频序列多目标优化问题。IM-MOEA/D与NAS-MOEA的优化性能虽然优于LMEA与LMOCSO，但差于LSMaODE与LSMaODE-FHS，这说明更为精细的分组策略和进化方法对优化性能有所提升，但优化程度仍旧不足，得到跳频序列集的各项指标还是较差。LSMaODE采用增强搜索的方法，对决策变量进行整体优化，在N=128、N=256时，取得了质量较高的解集，但随着决策变量的增加，得到跳频序列集的最大汉明自相关明显变差，但均匀性变好，这是由于 LSMaODE在RCD中对每个决策變量独立变异，更易找到均匀性更好的个体，而最大汉明自相关需要考虑到变量的顺序，所以在高维时难以优化。LSMaODE-FHS在所有测试中，取得了最好的HV指标和最好的最大汉明自相关，复杂度在高维时也能取得最好，均匀性虽差于LSMaODE，但差距不大，说明加入决策变量洗牌策略后，个体在RCD过程中具备更多变异可能，因此最大汉明自相关和复杂度的优化更为充分，再配合反向差分进化，使各项指标得到均衡优化，从而得到收敛性和多样性更好的解集。

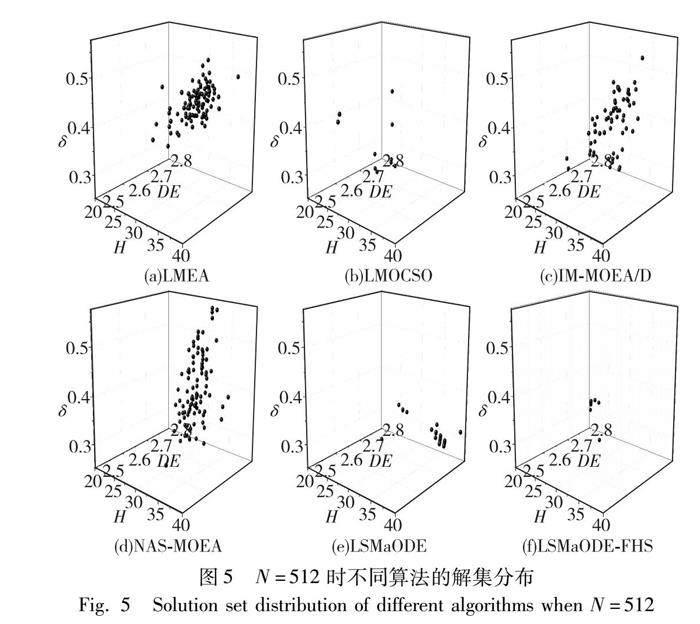
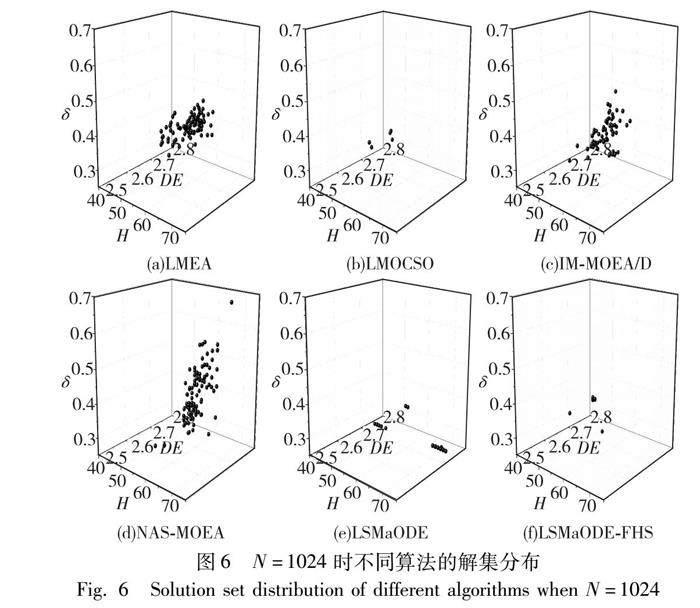
为进一步对算法性能进行分析，给出不同决策变量维度下各算法的解集在目标空间的分布，如图3～6所示。

LMEA解集分布位置较差，说明聚类分组的方法在跳频序列多目标问题中的优化程度不足，得到的跳频序列指标较差。LMOCSO虽然分布位置与LSMaODE和LSMaODE-FHS近似，但多出了很多优化不均衡的个体，说明竞争粒子群优化的进化方式对跳频序列的各项指标存在顾此失彼的情况。IM-MOEA/D与NAS-MOEA的解集分布都较为分散，且各项性能指标明显不够优秀，说明IM-MOEA/D与NAS-MOEA的优化不够充分，解集在目标空间上没有充分逼近Pareto前沿。在N=128时，LSMaODE与LSMaODE-FHS解集分布近似；在N=256、N=512、N=1 024时，LSMaODE解集的分布在最大汉明自相关上更大，而LSMaODE-FHS加入决策变量洗牌策略，因此分布位置更好，同时反向差分进化增强了算法寻优能力，避免了优化不均衡个体的出现。

综合来看，相较于其他大规模多目标优化算法，LSMaODE-FHS在跳频序列多目标优化模型中具有更好的寻优能力，得到的解集具有更好的收敛性和多样性，对应的跳频序列集性能指标综合更好。

3.2 抗干扰性能分析

抗干扰性能分析基于某军用跳频通信设备，信息脉冲共32 bit，脉宽0.5 μs，采样频率200 MHz，上采样倍数为100倍。脉冲成型采用根升余弦滚降滤波器，滚降参数R=0.22，码元速率0.5 MHz，基带滤波采样速率2 MHz，工作带宽为3 MHz～35 MHz，跳频间隔为1 MHz，频点数q=32，跳频序列长度N=512。

令发送时间为10 s，考虑到实际情况中的多变干扰环境，将发送分为前后半段，构建多种干扰环境，如表5所示。

将文献［7］得到的跳频序列集定义为FHS1，文献［8］得到的跳频序列为FHS2，文献［11］得到的跳频序列为FHS3，本文方法得到的跳频序列集为FHS4。

设置干扰信噪比为-10 dB到0 dB，每间隔2 dB进行30次测试。对FHS1和FHS4，在测试中对跳频序列集中的每个序列进行分别测试，并将误码率取平均值，作为最终的结果。计算不同设计方法在不同干扰环境中的误码率，如图7～10所示。

FHS1与FHS2的误码率较为接近，这主要是由于两者均能实现较长的跳频序列，但FHS1仅考虑汉明相关性，而FHS2基于混沌系统，两者参与的性能指标不足，所以误码率相较于FHS4略高。FHS3基于优化算法对加权目标函数进行优化，在大规模优化中普通优化算法难以收敛，且只能针对一种干扰类型，因此误码率大幅上升。FHS4在各干扰环境中均保持了较低误码率，说明跳频序列多目标优化模型能够设计出具有较强适应力的跳频序列集，且LSMaODE-FHS能够保证长序列的抗干扰能力。

4 结束语

本文对跳频序列的设计问题进行了研究，通过分析现有设计方法的优缺点，针对跳频序列设计中优化目标少、决策变量规模小的问题，提出基于大规模多目标优化的跳频序列设计方法。综合考虑跳频序列的最大汉明自相关、复杂度和均匀度，结合大规模多目标优化理论，提出LSMaODE-FHS算法，在RCD中加入决策变量洗牌策略以提高非支配集的多样性，在NGRI中加入反向差分进化，将候选个体的反向个体参与到差分进化中，提高算法寻优能力。

该方法从大规模多目标优化的角度入手，在高维决策变量情况下，对各优化目标进行同时优化，以兼顾跳频序列的各项性能指标，更贴合跳频序列的实际使用需求。此外，该方法一次可以得到多个跳频序列，在实际使用中可以随时变更跳频序列，相较于单目标优化具有更高的使用价值和保密性。

参考文献：

［1］刘鑫，陈璐瑶，姚昌华，等. 一种新型的增强型差分跳频通信抗干扰系统 ［J］. 计算机应用研究，2022，39（6）： 1820-1824. （Liu Xin，Chen Luyao，Yao Changhua，et al. Novel anti-jamming system for enhanced differential frequency hopping ［J］. Application Research of Computers，2022，39（6）： 1820-1824

［2］Alexandre F，Miguel L，André Z. A fair channel hopping scheme for lora networks with multiple single-channel gateways ［J］. Sensors，2022，14： 5260-5260.

［3］谭思炜，唐波，张林森，等. 跳频电磁引信干扰感知技术方案研究 ［J］. 系统工程与电子技术，2022，44（11）： 3330-3337. （Tan Siwei，Tang Bo，Zhang Linsen，et al. Interference sensing technical solution for frequency hopping electromagnetic fuze ［J］. Systems Engineering and Electronics，2022，44（11）： 3330-3337.）

［4］Yin Wenjuan，Xiang Can，Fu Fangwei. New frequency-hopping sequence sets with good parameters under aperiodic hamming correlation ［J］. Cryptography and Communications，2022，15（1）： 159-169.

［5］Zhou Limengnan，Liu Xing. Families of optimal low-hit-zone frequency-hopping sequence sets under the periodic partial hamming correlation properties ［J］. IEEE Access，2020，8： 14991-14998.

［6］Fan Mingyue. Frequency-hopping sequences with optimal average Hamming correlation and their applications in energy and spectrum harvesting technologies area ［J］. IEEE Access，2021，9： 1388-1393.

［7］Niu Xianhua，Xing Chaoping，Yuan Chen. Asymptotic Gilbert-Varshamov bound on frequency hopping sequences ［J］. IEEE Trans on Information Theory，2020，66（2）： 1213-1218.

［8］楊宇晓，汪德鑫，黄琪. 四维超混沌射频隐身跳频通信设计方法 ［J］. 宇航学报，2020，41（10）： 1341-1349. （Yang Yuxiao，Wang Dexin，Huang Qi. Design method of radio frequency stealth frequency hopping communications based on four-dimensional hyperchaotic system ［J］. Journal of Astronautics，2020，41（10）： 1341-1349.）

［9］Jung J，Lim J，Park S，et al. Analysis of low probability of detection capability for chaotic standard map-based FH-OFDMA system ［J］. Applied Sciences，2021，11（5）： 2198-2198.

［10］刘鹏飞，杜欣军. 基于加权反馈三维混沌系统的调制跳变通信 ［J］. 计算机工程，2021，47（3）： 183-189，195. （Liu Pengfei，Du Xinjun. Modulation hopping communication based on three-dimensional chaotic system with weighted feedback ［J］. Computer Engineering，2021，47（3）： 183-189，195.）

［11］赵知劲，王安强，尚俊娜，等. 基于灰狼算法的抗干扰跳频序列设计 ［J］. 信号处理，2021，37（6）： 1046-1054. （Zhao Zhijin，Wang Anqiang，Shang Junna，et al. Design of anti-jamming frequency-hopping sequence based on grey wolf algorithm ［J］. Journal of Signal Processing，2021，37（6）： 1046-1054.）

［12］黄琪，杨宇晓，江陈卓. 组合跳变随机平移宽间隔混沌跳频序列设计 ［J］. 电讯技术，2022，62（6）： 755-761. （Huang Qi，Yang Yuxiao，Jiang Chenzhuo. Design of combined-hopping-random-shift wide-gap chaotic frequency hopping sequences ［J］. Telecommunication Engineering，2022，62（6）： 755-761.）

［13］Cao Bin，Fan Shanshan，Zhao Jianwei，et al. Quantum-enhanced multiobjective large-scale optimization via parallelism ［J］. Swarm and Evolutionary Computation，2020，57： 100697.

［14］Tian Ye，Si Langchun，Zhang Xingyi，et al. Evolutionary large-scale multi-objective optimization： a survey ［J］. ACM Computing Surveys，2021，54（8）： 1-34.

［15］Lempel A，Greenberger H. Families of sequences with optimal Hamming correlation properties ［J］. IEEE Trans on Information Theory，1974，20（1）： 90-94.

［16］Rostaghi M，Azami H. Dispersion entropy： a measure for time series analysis ［J］. IEEE Signal Processing Letter，2016，23（5）： 610-614.

［17］甘良才，吳燕翔. 一类混沌映射产生跳频序列的方法 ［J］. 电子学报，2000，28（4）： 109-111. （Gan Liangcai，Wu Yanxiang. Genera-ting FH sequences by a class of chaotic maps ［J］. Acta Electronica Sinica，2000，28（4）： 109-111.）

［18］Hong Wenjing，Yang Peng，Tang Ke. Evolutionary computation for large-scale multi-objective optimization： a decade of progresses ［J］. International Journal of Automation and Computing，2021，18（2）： 1-15.

［19］Zhang Maoqing，Wang Lei，Guo Weian，et al. Many-objective evolutionary algorithm based on relative non-dominance matrix ［J］. Information Sciences，2021，547： 963-983.

［20］Zhang Xingyi，Tian Ye，Cheng Ran，et al. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization ［J］. IEEE Trans on Evolutionary Computation，2018，22（1）： 97-112.

［21］Liu Songbai，Lin Qiuzhen，Tian Ye，et al. A variable importance-based differential evolution for large-scale multiobjective optimization ［J］. IEEE Trans on Cybernetics，2022，52（12）： 13048-13062.

［22］Tian Ye，Lu Chang，Zhang Xingyi，et al. Solving large-scale multi-objective optimization problems with sparse optimal solutions via unsupervised neural networks ［J］. IEEE Trans on Cybernetics，2021，51（6）： 3115-3128.

［23］Chen Huangke，Cheng Ran，Wen Jinming，et al. Solving large-scale many-objective optimization problems by covariance matrix adaptation evolution strategy with scalable small subpopulations ［J］. Information Sciences，2020，509（C）： 457-469.

［24］Tian Ye，Zheng Xiutao，Zhang Xingyi，et al. Efficient large-scale multiobjective optimization based on a competitive swarm optimizer ［J］. IEEE Trans on Cybernetics，2019，50（8）： 1-13.

［25］Zhang Kai，Shen Chaonan，Yen G G. Multipopulation-based differential evolution for large-scale many-objective optimization ［EB/OL］. （2022-06-22） ［2023-08-09］. http：//doi. org/10. 1109/TCYB. 2022. 3178929.

［26］Zhang Kai，Shen Chaonan，Yen G G，et al. Two-stage double niched evolution strategy for multimodal multiobjective optimization ［J］. IEEE Trans on Cybernetics，2022，25（4）： 754-768.

［27］Zhang Kai，Xu Zhiwei，Xie Shengli，et al. Evolution strategy-based many-objective evolutionary algorithm through vector equilibrium ［J］. IEEE Trans on Cybernetics，2021，51（11）： 5455-5467.

［28］Tizhoosh H R. Opposition-based learning： a new scheme for machine intelligence ［C］//Proc of International Conference on Computational Intelligence for Modelling，Control and Automation.Piscataway，NJ： IEEE Press，2005： 695-701.

［29］Zitzler E，Thiele L. Multiobjective evolutionary algorithms： a compa-rative case study and the strength Pareto approach ［J］. IEEE Trans on Evolutionary Computation，1993，3（4）： 257-271.

［30］Lucas R C，Aluizio F R. IM-MOEA/D： an inverse modeling multi-objective evolutionary algorithm based on decomposition ［C］// Proc of IEEE International Conference on Systems，Man，and Cybernetics. Piscataway，NJ：IEEE Press，2021： 462-467.

［31］閆世瑛，颜克斐，方伟，等. 基于差分进化邻域自适应的大规模多目标算法 ［J］. 系统工程与电子技术，2022，44（7）： 2112-2124. （Yan Shiying，Yan Kefei，Fang Wei，et al. Large-scale multi-objective algorithm based on neighborhood adaptive of differential evolution ［J］. Systems Engineering and Electronics，2022，44（7）： 2112-2124.）