增强组合差分乘积形态学滤波的轴承故障特征提取方法
2024-05-23徐先峰赵卫峰邹浩泉宋亚囡
徐先峰 赵卫峰 邹浩泉 宋亚囡
收稿日期：2021-12-01
网络出版日期：2022-04-27
基金项目：陕西省自然科学基础研究计划资助项目（2019JQ-678）；陕西省重点研发计划资助项目（2021GY-098）；西安市智慧高速公路信息融合与控制重点实验室资助项目（ZD13CG46）；长安大学中央高校基本科研业务费专项资金资助项目（300102321504，300102321501，300102321503）。
作者简介：徐先峰（1982—），男，副教授，博士，主要从事信号处理、深度学习理论及应用和智能电网研究，（E-mail）xxf_chd@163.com。
摘要：针对滚动轴承故障信号的非线性、非平稳、强噪声特性导致的常规时频域特征提取方法受限问题，提出一种增强组合差分乘积形态学滤波的轴承故障特征提取方法。在分析数学形态学4种基本运算的正、负冲击脉冲提取特性的基础上，运用级联、差分、乘积构造的一种新的组合差分乘积算子（combination difference multiply operator， CDMO）具备了同时提取正、负冲击脉冲的能力，并发挥梯度乘积运算对脉冲提取更敏感的优势，实现故障信息的充分提取。引入故障特征频率比指标优化CDMO结构元素参数，修正待处理信号的几何特征，提取与结构元素相匹配的信号特征信息。在CDMO滤波的基础上，借助三阶累积量切片谱技术能够抑制高斯噪声、突出二次耦合分量的优势，准确提取故障特征频率及其倍频，增强轴承故障特征提取能力并抑制噪声干扰。依托2种不同来源的工程实际信号并与经典故障特征提取方法对比分析，验证了所提方法的有效性。
关键词：滚动轴承；形态学滤波；三阶累积量切片谱；特征提取
中图分类号：TH113 文献标志码：A 文章编号：1000-582X（2024）03-096-11
滚动轴承作为机械设备的易损核心部件，对整个机械设备的稳定运行起决定性作用，研究其故障诊断方法对实际工程意义重大[1]。滚动轴承原始振动信号具有非线性、非平稳以及噪声干扰强的特点，且噪声信号多呈现高斯特性[2]，从中提取微弱故障特征是滚动轴承故障诊断的关键[3]。
短时傅里叶变换、小波变换、经验模态分解等时频域方法可以实现轴承故障特征提取[4-6]。何强等[4]对轴承振动信号进行短时傅里叶变换，输入语义卷积神经网络（semantic convolutional neural network，SeCNN）进行故障分类，针对小样本数据获得了准确有效的实验结果。但是，短时傅里叶变换无法同时对高频和低频信号进行有效分析。范春旸等[5]提出一种基于小波变换结合随机森林的故障分析模型，能选择出对故障状态较为重要的特征，但是，选取恰当的基函数存在困难。经验模态分解方法也存在模式混叠、对噪声敏感等不足[6]。
数学形态学是一种适合于非线性、非平稳过程的抗噪声信号处理方法，通过结构元素（structuring element，SE）修正待处理信号的几何特征，降噪能力好，计算简单[7]，近年来在机械故障诊断领域得到了广泛应用。目前，关于形态学滤波方法的研究多集中于决定故障特征提取效果的形态学算子构造与结构元素参数确定两方面。Li等[8]提出加权多尺度形态学梯度滤波（weighted multi-scale morphology gadient，WMMG），改进了传统多尺度形态学滤波的特征提取能力，但其权重系数配比不易寻优，在一定程度上弱化了个别尺度作用较强的结果所包含的特征信息。Lv等[9]将4种基本形态学算子进行平均组合差分以突出故障特征的周期性脉冲，但平均组合差分效果不及乘积运算。Li等[10]提出一种形态学梯度乘积算子，并结合高阶谱分析方法—三阶累积量切片谱提取轴承故障特征，获得了良好的效果，但仅采用开闭2种算子组合，限制了其特征提取与噪声抑制能力。实际轴承运行工况愈加复杂，导致原始振动信号中涵盖大量噪声信号，因此，需要进一步增强轴承故障特征的提取能力。
为了充分利用数学形态学针对非线性、非平稳过程的抗噪声处理能力，避免多尺度形态学滤波权重系数配比不易寻优的缺点，有效发挥形态学算子乘积组合比平均组合更能突出故障信号周期性脉冲特征的优势，提出了一种增强组合差分乘积形态学滤波（enhanced combination difference multiply morphological filter，ECDMMF）的轴承故障特征提取方法。在充分研究了4种基本形态学算子对正负脉冲提取性能的基础上，通过对同类算子级联、差分、乘积，进而构造一种新的组合差分乘积算子（combination difference multiply operation，CDMO），以獲取更多的脉冲信息，结合故障特征频率比（characteristic frequency radio，CFR），优化乘积算子的SE参数，从而提取与SE相匹配的信号特征信息。在此基础上，借助三阶累积量切片谱技术（third-order cumulant slice spectrum，TOCSS）能够有效抑制高斯噪声、突出二次耦合成分的优点，提取轴承故障数据特征频率及倍频，进一步增强故障特征提取能力。
1增强组合差分乘积形态学滤波方法
1.1新形态算子构造
1.1.1 基本形态学算子定义及其特性分析
基本的形态学算子有4种：膨胀、腐蚀、闭合、打开。假定代表定义域为的一维离散信号函数，代表定义域为的结构元素离散函数，其中。基本算子膨胀（dilation）与腐蚀（erosion）定义如下：
轴承故障一维振动信号包含周期性冲击脉冲特征，以上4种基本形态学算子都可以用于提取脉冲特征，但其表现出不同的脉冲特征提取性能[11]，如表1所示。
由表1可知，利用腐蚀与打开运算可以提取轴承故障信号中的负冲击特征，利用膨胀与闭合运算可以提取正冲击特征；4种基本算子根据对冲击特征的提取性能可分为2类：提取正冲击的膨胀与闭合运算，提取负冲击的腐蚀与打开运算。对同类形态算子进行级联、组合能够进一步提升其冲击特征提取能力，同时保证特征提取的完整性。
1.1.2 组合差分乘积算子
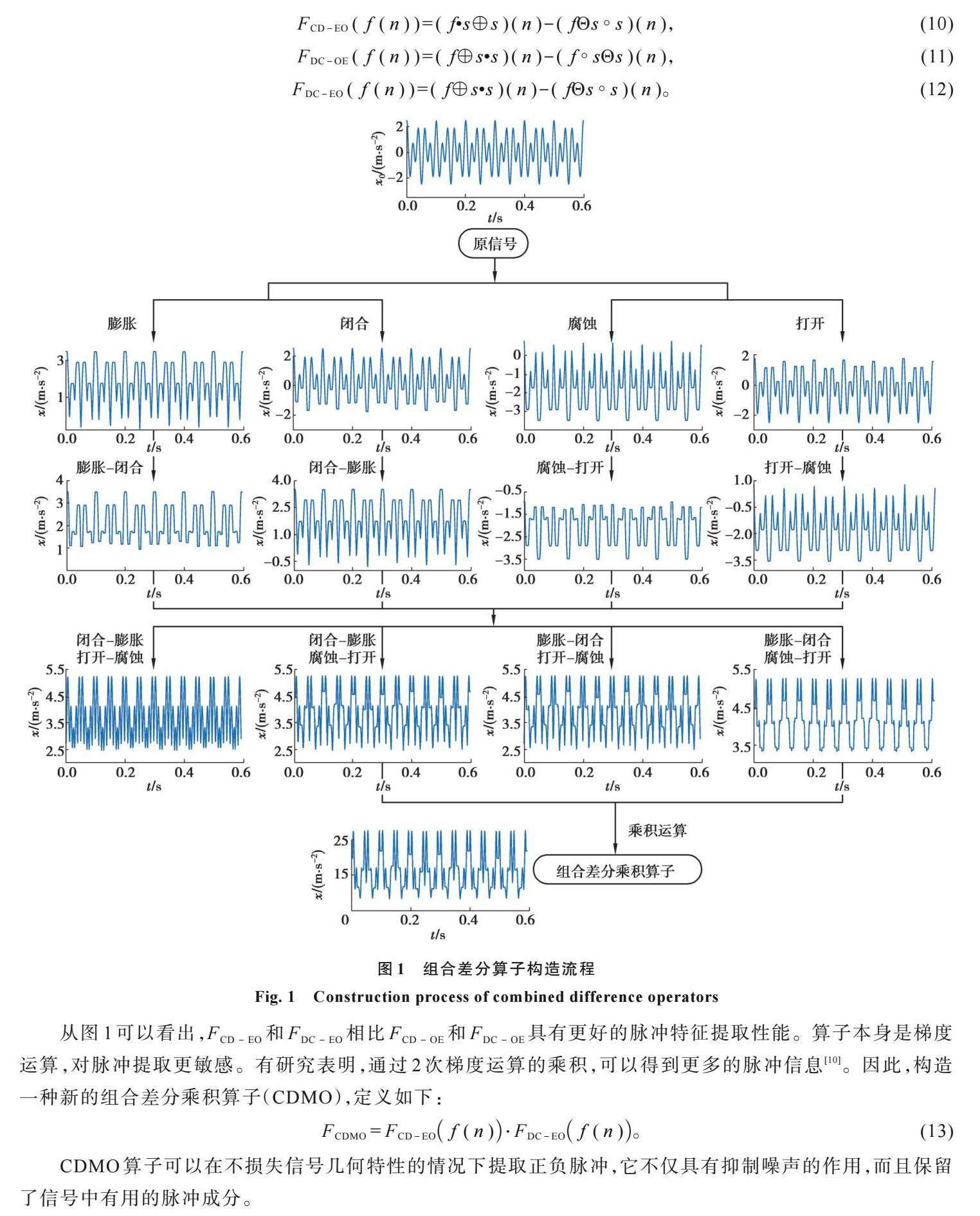
图1是根据4种基本算子构造组合差分乘积算子的流程，利用仿真信号
说明了该算子对脉冲提取效果的有效性，其中t为时间，x0为输入原信号。
从图1可以看出，膨胀运算消除了负脉冲，使正脉冲更加平滑，腐蚀运算消除了正脉冲，使负脉冲更加平滑，而闭合运算保留了正脉冲，消除了负脉冲，打开运算消除了正脉冲，保留了负脉冲。
CDMO算子可以在不损失信号几何特性的情况下提取正负脉冲，它不仅具有抑制噪声的作用，而且保留了信号中有用的脉冲成分。
1.2三阶累积量对角切片谱
高斯噪声是轴承故障信号中最常见的噪声之一，任何周期性和准周期性信号都可以被认为是非高斯信号，也可以被认为是滚动轴承自发产生的信号[2]。因此，发生故障的轴承的振动信号基本上是非高斯信号，但因为运行环境的影响，还包含干扰信号分量，即高斯信号。高斯信号的高阶谱为零，通过高阶累积量变换可以去除，进而去除轴承振动信号中的噪声干扰。
典型高阶累积量变换技术——三阶累积量切片谱可用于抑制高斯噪声，同时具有抑制非二次相位耦合成分、计算量小的特点[12]。通过该方法提取轴承故障数据特征频率及其倍频，能够突出特征，增强故障特征提取能力，其基本原理如下。
1.3基于CFR指标的结构元素参数优化
在形态学滤波中，结构元素SE的设置对形态学滤波器的有效性有显著的影响。SE参数由形状、高度和长度3个要素决定，形状对滤波效果的影响不大，为了减少计算量并提高计算效率，选择与一维轴承振动信号形状相似的零高度直线型结构元素，主要考虑SE长度
对形态算子滤波性能的影响。
故障特征频率比（CFR）是一种评价周期性脉冲提取效果的新指标，对轴承局部故障产生的特征信号比较敏感[14]。因此，选取CFR作为衡量不同
下，ECDMMF方法滤波性能的标准。CFR指标值定义如下：
1.4ECDMMF方法实现流程
增强组合差分乘积形态学滤波（ECDMMF）的轴承故障特征提取方法将新的形态学算子CDMO与TOCSS技术结合处理轴承故障原始信号。该方法实现流程如图3所示。
根据流程图，该方法实现步骤如下。
2实验结果与分析
2.1轴承故障信号实验
实际工程应用中信号运行环境更加复杂，所采集振动信号噪声干扰更强，本研究中基于外圈故障（outer-race fault，OF）及内圈故障（inner-race fault，IF）信號实测数据验证所提方法有效性。
2.2轴承外圈故障实验
2.2.1 IMS轴承全寿命周期数据
利用辛辛那提大学智能维护系统（IMS）的轴承数据验证本节方法[16]。轴承故障实验装置如图4所示。在全寿命周期数据采集过程中，每个轴承上通过2个PCB353B33加速度器记录其转动中的加速度，每10 min记录1次，共984组数据。实验完成后，发现轴承1出现了外圈故障。
实验中所使用轴承的相关参数如表2所示。实验载荷恒定为26.6 kN，电机转速为2 000 r/min，采样频率为20 kHz。根据式（18）计算外圈故障特征频率理论值可得=236.4 Hz。
2.2.2 ECDMMF方法实验结果
根据2.2.1节介绍，选取IMS第541组数据进行分析，数据长度为8 192，提取其外圈故障的特征频率。轴承早期故障原始信号的分析结果如图6所示，包括时域波形、频谱以及包络谱，其中为幅值。
从图6（b）频谱图中可以看出，外圈故障特征频率很大程度上被噪声分量掩盖，无法提取236 Hz的频率分量。图6（c）的包络谱中存在明显的几个频率分量，但其均为转频33 Hz的倍频，与外圈故障特征频率无关；包络谱中虽然可观察到故障特征频率分量，但与其他频率分量幅值相比，其在包络谱中并不突出。因此，仅依靠频谱或者包络谱无法提取由外圈故障导致的微弱脉冲特征，难以准确判断轴承的故障类型。
利用ECDMMF方法处理IMS轴承故障信号，根据外圈故障特征频率理论计算值以及采样频率，设定范围为。各参数下ECDMMF方法滤波结果的CFR指标值如图7（a）所示；在为3时，CFR指标最大，认为此时的滤波结果最佳，其TOCSS如图7（b）所示。
从图中可以看出4组幅值最突出的频率分量为230 Hz及其倍频。230 Hz与外圈故障特征频率理论值236 Hz非常接近，误差可能是由于一些滤波过程中的计算误差引起，在可接受的范围之内。ECDMMF方法分析处理IMS轴承故障信号后，抑制了噪声干扰，准确提取出外圈故障的微弱脉冲，使其在其他频率分量中具有较高的幅值。由此可以判斷该轴承的故障类型为外圈故障。
2.3轴承内圈故障实验
2.3.1 XJTU-SY轴承全寿命周期数据
由于IMS轴承数据集仅有一种工况下的实验，数据样本比较单一，为了避免单一数据样本无法全面验证ECDMMF方法有效性的情况，采用西安交通大学的轴承全寿命周期数据（XJTU-SY）验证ECDMMF方法的有效性。实验所用的轴承加速寿命测试平台（图8）由交流电机、转速控制器、转轴等组成，通过液压加载系统和转速控制器调节径向力和转速，以实现不同工况的模拟。该实验共设计了3种工况，每种工况下有5个轴承[17]。
实验中所用轴承为LDK UER滚动轴承，其相关参数如表3所示。选取径向力为10 kN、电机转速为2 400 r/min工况条件下第3个轴承的一段内圈故障信号进行研究，信号由水平方向加速度传感器采集，采样频率为25.6 kHz。根据轴承相关参数由式（19）计算可得内圈故障特征频率理论值=196.67 Hz。
所选取工况下的轴承共采集了371组样本，每组样本采样时长为1.28 s，样本间的采样间隔为1 min。
类似IMS数据集中关于轴承全生命周期的划分，计算371组样本的，如图9所示。选取最早出现波动的第341组数据研究，此时可能已经发生早期故障。
2.3.2 ECDMMF方法实验结果
采用XJTU-SY轴承数据，选取第341组水平方向加速度信号进行分析，数据长度为8 192，图10所示为原始数据时域波形、频谱及包络谱。从图10（b）中能够发现，频率分量集中在1 000 Hz处，并且低频段噪声干扰多，无法从频谱图中提取。从图10（c）中可以得到197 Hz的频率分量，接近内圈故障频率196.67 Hz，但其幅值非常小，并且在200 Hz前出现很多幅值较高的无法解释来源的频率分量。因此，仅通过频谱或者包络谱分析无法进行故障诊断。
利用ECDMMF方法处理XJTU-SY轴承故障原始信号，根据其采样频率以及内圈故障理论频率值计算优化范围为。各对应ECDMMF滤波结果的
指标值如图11（a）所示，最优形态学滤波结果的TOCSS如图11（b）所示。
从图中可以看出，LSE=16时，CFR指标值最大，此时将获得最优滤波结果。最优滤波结果的TOCSS所对应的0～600 Hz频率区间内包含很多明显的脉冲，其对应的数值都接近于转频=40 Hz以及内圈故障频率=196.67 Hz的组合频率。ECDMMF方法有效地提取了转频以及内圈故障频率的一倍频、二倍频及三倍频，并且滤波结果中包含的噪声干扰分量非常少。由此可以判断该轴承发生了内圈故障。
2.4对比分析
为了说明所提算法的有效性，将其与经典的WMMG方法[8]以及近年来新提出的增强形态梯度乘积滤波（enhanced morphology gradient product filter， EMGPF）方法[10]进行对比。
按照文献[8]所述WMMG方法形态学算子以及多尺度加权方法，处理IMS外圈以及XJTU-SY内圈故障信号，其滤波结果如图12所示。
从图12（a）中可以得出，WMMG方法能够准确提取转频
及外圈故障信号的故障特征频率，这2个频率分量幅值最高。但是在分量附近仍然包含比较明显的干扰分量脉冲，未提取出故障特征频率的倍频脉冲分量，且100 Hz以后并无有价值的脉冲分量，未体现轴承周期性冲击性脉冲特征。从图12（b）中可以得出，WMMG方法能够提取转频及其二倍频、内圈故障特征频率，并且幅值最高。但是，内圈故障特征频率倍频的提取效果不佳，从频谱中无法得出倍频的脉冲分量。
相较于经典WMMG方法，本文所提ECDMMF方法不仅避免了多尺度加权方法的寻优问题，同时准确提取了轴承故障特征及其倍频分量，最大程度抑制噪声分量，为故障诊断提供了依据。
按照文献[10]所述EMGPF方法实现细节处理IMS外圈以及XJTU-SY内圈故障信号，其滤波结果如图13所示。
从图13（a）可知，该方法能提取IMS信号
的一倍频、二倍频及三倍频，但其二倍频及三倍频脉冲幅值较低。ECDMMF方法不仅可以提取较突出及高幅值的二倍频、三倍频脉冲，而且可以提取四倍频脉冲。相较于EMGPF方法，ECDMMF方法抑制噪声的能力更好，尤其在频段Hz处。
从图13（b）可知，EMGPF方法同样能提取XJTU-SY信号的以及的组合频率分量，只有个别组合分量有差异。例如EMGPF未提取出的频率分量，并且ECDMMF方法提取脉冲的幅值更高，尤其是在众多有用分量中，内圈故障特征频率分量及其倍频更加突出。此外，ECDMMF滤波结果中噪声干扰分量的毛刺更少，幅值更低，而EMGPF滤波结果在0～300 Hz处存在更多毛刺。
根据2种方法的原理，两者的不同之处在于形态学算子的不同。可见，经过4种基本运算中同类算子级联、差分组合之后比仅根据开闭算子组合具有更强的特征提取与抑制噪声的能力。
3結束语
为确保准确提取轴承信号故障特征频率，进一步增强故障特征提取能力，提出了ECDMMF方法。基于数值实验并依托工程应用案例与经典的多尺度形态学滤波方法WMMG对比研究，结果表明ECDMMF方法能够更加准确地提取轴承故障特征频率及倍频，所提取的与故障特征频率相关的分量更完整，并且与噪声干扰分量相比幅值更高，更易进行故障类别判断。通过与EMGPF形态学滤波方法对比研究，表明新的组合差分乘积算子比仅根据2种形态运算构造的乘积算子的故障特征提取效果更好。
参考文献
［1］ Li H， Liu T， Wu X， et al. Enhanced frequency band entropy method for fault feature extraction of rolling element bearings[J]. IEEE Transactions on Industrial Informatics， 2020， 16（9）： 5780-5791.
［2］ Li Y F， Liang X H， Zuo M J. Diagonal slice spectrum assisted optimal scale morphological filter for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing， 2017， 85： 146-161.
［3］ Lv C， Zhang P L， Wu D H， et al. Bearing fault signal analysis based on an adaptive multiscale combined morphological filter[J]. International Journal of Rotating Machinery， 2020， 2020（10）： 1-8.
［4］ 何强， 唐向红， 李传江， 等. 负载不平衡下小样本数据的轴承故障诊断[J]. 中国机械工程， 2021， 32（10）： 1164-1171， 1180.
He Q， Tang X H， Li C J， et al. Bearing fault diagnosis method based on small sample data under unbalanced loads[J]. China Mechanical Engineering， 2021， 32（10）： 1164-1171， 1180.（in Chinese）
［5］ 范春旸， 吴守鹏， 刘晓文， 等. 基于小波包变换与随机森林的滚动轴承故障特征分析方法[J]. 机械设计与制造， 2020（10）： 59-63， 70.
Fan C Y， Wu S P， Liu X W， et al. Fault feature analysis method of rolling bearing based on wavelet packet transform and random forest[J]. Machinery Design & Manufacture， 2020（10）： 59-63， 70.（in Chinese）
［6］ Gao S Z， Wang Q， Zhang Y M. Rolling bearing fault diagnosis based on CEEMDAN and refined composite multiscale fuzzy entropy[J]. IEEE Transactions on Instrumentation and Measurement， 2021， 70： 1-8.
［7］ Meng L J， Xiang J W， Wang Y X， et al. A hybrid fault diagnosis method using morphological filter-translation invariant wavelet and improved ensemble empirical mode decomposition[J]. Mechanical Systems and Signal Processing， 2015， 50/51： 101-115.
［8］ Li B， Zhang P L， Wang Z J， et al. A weighted multi-scale morphological gradient filter for rolling element bearing fault detection[J]. ISA Transactions， 2011， 50（4）： 599-608.
［9］ Lv J X， Yu J B. Average combination difference morphological filters for fault feature extraction of bearing[J]. Mechanical Systems and Signal Processing， 2018， 100： 827-845.
［10］ Li Y F， Zuo M J， Chen Y J， et al. An enhanced morphology gradient product filter for bearing fault detection[J]. Mechanical Systems and Signal Processing， 2018， 109： 166-184.
［11］ 臧怀刚， 刘子豪， 李玉奎. 基于形态滤波和Laplace小波的轴承故障诊断[J]. 中国机械工程， 2016， 27（9）： 1198-1203.
Zang H G， Liu Z H， Li Y K. Fault diagnosis of bearings based on morphological filter and Laplace wavelet[J]. China Mechanical Engineering， 2016， 27（9）： 1198-1203.（in Chinese）
［12］ Jie B A， Huo C Q， Yu J J. Fault feature detection of rolling bearing based on LMD and third-order cumulant diagonal slice spectrum[J]. Applied Mechanics and Materials， 2016， 851： 333-339.
［13］ Nikias C L， Mendel J M. Signal processing with higher-order spectra[J]. IEEE Signal Processing Magazine， 1993， 10（3）： 10-37.
［14］ Wu D Y， Wang J W， Wang H， et al. An automatic bearing fault diagnosis method based on characteristics frequency ratio[J]. Sensors， 2020， 20（5）： 1519.
［15］ Dong Y B， Liao M F， Zhang X L， et al. Faults diagnosis of rolling element bearings based on modified morphological method[J]. Mechanical Systems and Signal Processing， 2011， 25（4）： 1276-1286.
［16］ The National Aeronautics and Space Administration. IMS data set [DS/OL]. [2021-08-07]. https：//ti.arc.nasa.gov/project/prognostic-data-repository.
［17］ 雷亚国， 韩天宇， 王彪， 等. XJTU-SY滚动轴承加速寿命试验数据集解读[J]. 机械工程学报， 2019， 55（16）： 1-6.
Lei Y G， Han T Y， Wang B， et al. XJTU-SY rolling element bearing accelerated life test datasets： a tutorial[J]. Journal of Mechanical Engineering， 2019， 55（16）： 1-6.（in Chinese）
（編辑 吕建斌）
