基于多模型自适应方法的智能汽车路径跟踪控制
2024-05-23梁艺潇李以农AmirKhajepour郑玲余颖弘张紫微
梁艺潇 李以农 Amir Khajepour 郑玲 余颖弘 张紫微

收稿日期:2021-11-16
网络出版日期:2022-04-13
基金项目:国家自然科学基金资助项目(51875061)。Foundation:Supported by National Natural Science Foundation of China (51875061).
作者简介:梁艺潇(1993—),男,博士,主要研究方向为智能车辆规控技术,(E-mail) liangyixiao1119@foxmail.com。
通信作者:李以農,男,博士,教授,博士生导师,(E-mail)ynli@cqu.edu.cn。
摘要:路径跟踪控制是智能汽车的一项核心技术,跟踪效果的精确性和在各种路面附着条件下的鲁棒性是该技术的两大关键要素。但汽车动力学模型的不确定性,尤其是轮胎侧偏刚度的摄动使这两者难以同时得到满足。针对这一问题,将多模型自适应理论引入到智能汽车运动控制中处理不确定性系统的控制。首先,推导了多模型自适应控制律,提出了凸包构架下各个顶点的子模型对真实模型的自适应逼近律,并通过李雅普诺夫函数证明了所提出自适应律的收敛能力。在此基础上建立了汽车动力学模型和车辆-路径联合模型,并由多个顶点子模型构建可覆盖汽车轮胎侧偏刚度摄动范围的凸多面体,利用汽车动力学模型求解自适应率,通过车辆-路径联合模型,基于线性二次型方法(linear quadratic regulator, LQR)求解各个顶点的子模型处的反馈控制律,并通过所得出的自适应权重进行加权。基于Carsim/Simulink的联合仿真结果表明,所提出的多模型自适应路径跟踪控制器在保证鲁棒性的同时克服了传统鲁棒控制方法的保守性问题,与基于名义模型的LQR控制器和鲁棒保性能控制器相比,在高附着路面和低附着路面上都可以取得更好的控制效果,很好地解决了路径跟踪控制中精确性与鲁棒性之间的两难问题。最后,通过快速原型测试平台对算法进行了进一步的实验验证。结果表明,所提出的多模型自适应算法实时性良好,具有较好的工程应用潜力。
关键词:智能汽车;车辆动力学;路径跟踪控制;模型不确定性;多模型自适应控制
中图分类号:U27 文献标志码:A 文章编号:1000-582X(2024)03-001-15
近年来,具有自动驾驶能力的智能汽车成了业界的研究热点[1-2]。路径跟踪控制是智能汽车的关键核心技术之一,旨在设计控制律使汽车完成对给定路径的跟踪。针对该问题,国内外学者展开了广泛的研究,提出了包括比例-积分-微分(proportion, integral, and differential, PID)[3]、模糊控制[4]、滑模控制[5]、最优控制[6]和模型预测控制[7-9]在内的多种路径跟踪算法。这些算法大致可分为2类:第1类的算法[3-4]不需要建立参考模型,将汽车的动力学特征视为一个“黑箱”,其转向控制的输出仅仅取决于路径跟踪的偏差,这类算法往往需要大量的参数标定,且在理论上无法验证控制器的可靠性;第2类算法[5-9]需要建立汽车运动学/动力学模型,并基于控制理论对模型进行推导或迭代,以求解出可以使跟踪偏差收敛的转角控制量。第2类算法与第1类算法相比在可靠性上有显著的提升,其中基于运动学模型的控制器,在中低车速和曲率较小的工况下可取得不错的控制效果。但是,第2类算法由于忽略了汽车的侧偏问题,不适用于车速较高以及会产生较大侧向加速度的工况,相比之下,基于动力学模型的控制器在智能汽车路径跟踪控制中效果更佳[5]。
然而,从系统动力学的角度来看,汽车是高度复杂的耦合的非线性系统,其动力学模型具有明显的不确定性[10],对于智能汽车路径跟踪控制来说,轮胎侧偏刚度的摄动是模型不确定性的主要来源,该值会随路面附着系数、载荷、轮胎侧偏角等参数的变化而变化[11]。这类不确定性问题严重制约了智能汽车路径跟踪控制在不同工况下的鲁棒性和精确性。为了解决这一问题,文献[12-16]中提出了鲁棒控制的方案,通过不确定性参数的上下界对动力学模型进行扩维分析,设计控制器使智能汽车即使在轮胎侧偏刚度偏离其标定名义值较多的恶劣工况下仍然能保证对跟踪偏差的收敛能力。该类方法有效地提升了智能汽车路径跟踪控制的鲁棒性,保证了智能汽车在低附着等条件下的控制性能。可是,由于鲁棒控制方法往往基于最恶劣的条件展开研究,所设计的控制器为了保证鲁棒性,在控制精确性上做了妥协,往往具有较强的保守性。在高速公路、城市道路等路面附着条件较好时,其控制精确性往往不如基于名义模型所设计的控制器。
考虑以上因素,笔者基于多模型自适应理论[17]处理动力学模型不确定性系统的控制问题,解决路径跟踪控制中精确性与鲁棒性之间难以权衡的难题,设计智能汽车的路径跟踪控制器,通过建立多个已知参数的汽车动力学顶点模型组成可包含各个工况条件下侧偏刚度摄动的凸多面体,提出并证明具有偏差收敛能力的权值自适应律,建立车辆-路径的联合模型,在各个顶点处,基于线性二次型方法(linear quadratic regulator ,LQR)求解出反馈控制器,并进行相应的加权,实现多模型自适应的路径跟踪控制。由于凸多面体内任意一点都可以被各个顶点线性化地表示,所提出的控制器在保证鲁棒性的同时也不受鲁棒控制方法的保守性影响。Carsim-Simulink联合仿真的结果验证了本研究中提出方法的有效性和优越性。
1多模型自适应律推导
带有不确定参数的多输入多输出(multiple-input multiple-output,MIMO)线性系统可表示为
式中:t为时间;λ为系统中具有不确定性的参数;Ap(λ)和Bp(λ)是带有不确定性的状态空间方程矩阵,其不确定性取决于参数;xp(t)和u(t)分别代表系统的状态量和输入,二者都是可测的。
对于式(1)所述的系统,若存在N个已知的系统矩阵组合Ai和Bi(i=1,2,…,N),在N的数值、Ai和Bi的取值满足一定条件的基础上,对于任意可能的参数λ,不确定性矩阵可表示为[17]
式中,Co{·}代表一组矩阵集合的凸包,在几何上也可将其表示为一个凸多面体。
对于凸包中的每一个顶点i∈{1,2,…,N},其定参数动力学模型为
那么,由式(2)表示的矩阵集合的凸包含性质可以导出相应的自适应律。根据式(3),式(2)可被重新表示为
式中,wi(t)表示在t时刻每个顶点处子模型的权值,应满足以下条件:
式(5)中对于任意给定的λ,wi的值在线性时不变(linear time-invariant,LTI)系统中也是恒定的。
由于顶点处子模型的参数矩阵Ai和Bi是已知的,对未知的不确定性矩阵Ap(λ)和Bp(λ)的辨識可以等价于对未知权值wi的估计,这样就实现了问题的转化。针对系统的在线辨识问题,引入线性参数模型将式(2)写为[18]
式中:s表示微分算子;γ是恒定的正数;为推导计算中的算子。式(4)中的N个恒定顶点参数矩阵也可以类似地参数化:
式中。那么,各个顶点处子模型的估计偏差为
由式(4)和(5)可得
式(9)可用下面的矩阵表示:
基于式(5)和式(10)得到顶点处子模型中的最后一项,即第N项的权重为![]() 。因此,通过在式(10)的两端同时减去第N项模型的偏差εN(t),得到如下关系式:
。因此,通过在式(10)的两端同时减去第N项模型的偏差εN(t),得到如下关系式:
该式的导出为凸面体的权重辨识自适应律奠定了基础。将式(11)第一项中等式右端的项移到左端,并与ER(t)的转置相乘,可得
基于梯度下降法[17],设计如下权重估计的自适应律:
式中,Γ是用于调整收敛速率的对称正定矩阵。
此处,假设各个顶点的实际权重为![]() ,那么估计误差可表示为
,那么估计误差可表示为![]() 。将其代入式(11)中的第一项,可得
。将其代入式(11)中的第一项,可得
为了证明所提出的自适应律的收敛能力,定义李雅普诺夫函数
结合式(13)和式(14)得如下关系式:
对式(15)中的李雅普诺夫函数求导,并代入式(16)得
由此,自适应律(13)的收敛能力得到了证明。
需要注意的是,虽然该自适应律可以使偏差收敛,并满足式(5)中的第一项条件![]() ,但其并不能保证满足式(5)中的第二项条件,即wi(t)≥0,i=1,2,…,N。为了保证满足该条件,在自适应律中引入梯度投影法。首先,将式(5)中的约束表示为
,但其并不能保证满足式(5)中的第二项条件,即wi(t)≥0,i=1,2,…,N。为了保证满足该条件,在自适应律中引入梯度投影法。首先,将式(5)中的约束表示为
为了使式(18)具有式(5)的约束能力,函数g定义为
式中。
将S0和?S分别定义为S集的内部和边界,应用梯度投影法后,自适应律(13)可通过以下算法表示:
2智能汽车路径跟踪多模型自适应控制
2.1模型建立
在控制器的设计中,采用图1所示的二自由度简化车辆单轨动力学模型,该模型忽略了侧倾、俯仰、垂向运动和悬架的作用,在车辆动力学与控制领域中得到了广泛应用。其状态空间方程为[15]
式中:状态量,这里的vy和r分别是汽车的侧向速度和横摆角速度;输入,这里的δf为前轮转角;状态空间矩阵
式中:vx是汽车的纵向速度;m和Iz分别是汽车的质量和绕质心处垂向轴的转动惯量;lf和lr分别是汽车质心到前轴和后轴的距离;cf和cr分别表示前轮和后轮的侧偏刚度,其数值随路面附着系数、载荷、轮胎侧偏角等参数的变化而摄动,在一些较为极限的工况下,其真实值与名义值之间有极大的差異。对于汽车横向控制来说,侧偏刚度的摄动是模型不确定性的最显著体现。图1中X和Y是大地坐标系的坐标轴,Fyf和Fyr分别为前轮和后轮的侧偏力,αf和αr分别为前轮和后轮的侧偏角。
车辆实际位置与参考路径之间的相对关系如图2所示,图中ey是汽车的质心与参考路径上最近点d之间的横向偏差,S是沿参考路径的弧长,Ψd和Ψ分别是参考路径上的期望航向角与汽车的实际航向角,因而汽车的航向角偏差定义为ΔΨ=Ψ-Ψd。基于Serret-Frenet坐标系,通过小角度假设进行线性化,可得
将式(22)与式(23)结合得到由状态空间表示的车辆-路径联合模型的动力学方程(24),其中,状态量xc=[eyΔψvyr]T,控制输入量![]() ,扰动为k=[0vxρ 0 0]T。此外,基于状态量都可以准确测量/估计的假设,控制器将采用全状态反馈的方案。
,扰动为k=[0vxρ 0 0]T。此外,基于状态量都可以准确测量/估计的假设,控制器将采用全状态反馈的方案。
2.2自适应控制律
采用了如图3所示的4组侧偏刚度(cf1,cr1) (cf2,cr2) (cf3,cr3) (cf4,cr4)作为多模型自适应中顶点模型的侧偏刚度,取值自Carsim中的魔术轮胎模型,(cfn,crn)代表前后轴侧偏刚度的真实值。其中,(cf1,cr1)和(cf2,cr2)分别是在附着系数为1时的高附着路面下和轮胎侧偏角仅为0.5°时的侧偏刚度,其取值的差异是由于选择了不同的前后轴垂向载荷分布(汽车加/减速会影响前后轴的垂向载荷,进而影响前后轴轮胎侧偏刚度);(cf3,cr3)和(cf4,cr4)则分别为汽车在附着系数为0.2的低附着路面下和有较大轮胎侧偏角时的侧偏刚度。可以看出,这4组侧偏刚度组成的区域(图3中的阴影部分)可涵盖汽车在不同负载和不同路面附着等条件下的绝大多数情形,且区域内任何一个点都可以用4个顶点线性表示,由此实现了对不确定模型的凸包含。
整体的控制架构如图4所示。基于式(22)中的动力学模型来求解各个顶点的实时自适应权重,并以此对各个顶点对应车辆-路径联合模型(24)求得的状态反馈控制增益进行加权,实现多模型的自适应控制。
对各个顶点的车辆-路径联合模型,基于LQR方法设计控制器,使循迹偏差最小化,以保证汽车的动力学稳定性,其性能泛函为
式中:Q是半正定的状态量权重矩阵;R是正定的输入量权重。
相应地,最优反馈控制量表示为
式中:Ki为所计算的反馈增益;Pi是式(27)中Riccati方程的正定解。
因此,智能汽车多模型自适应路径跟踪控制的输入为
3仿真与分析
采用Simulink-CarSim联合仿真的方法对所提控制算法的效果进行验证。在Simulink中搭建控制算法,选取Carsim中的E型轿车作为仿真模型,其模型参数如表1所示。
选择常见的双移线工况对所提出控制算法进行验证,其曲率如图5所示。
在仿真中,汽车以60 km/h的速度分别在路面附着系数为0.85的高附着路面和路面附着系数为0.35的低附着路面完成双移线操作。为了更好地描述控制器的效果,引入了其他2组控制器进行对比:对比控制器1基于名义模型,采用LQR方法设计控制器,在仿真图表中简称为LQR;对比控制器2引入了文献[13]中采用的鲁棒保性能(robust-guaranteed-cost,RGC)控制器,该控制器在最优控制器架构的基础上,基于线性矩阵不等式方法(linear-matrix-inequality,LMI)对轮胎侧偏刚度摄动的上下界进行扩维,由此求解出最优的反馈增益,在图表中简写为RGC。本研究中所设计的多模型自适应控制器简写为MMAC。为了实现更客观的对比,对3组控制器采用了同样的权重矩阵Q和R。此外,仿真中的多模型自适应控制所采用的4个顶点模型的前后轴轮胎刚度分别为:(140 000,110 000) (110 000,140 000) (30 000,20 000) (20 000,30 000),单位为N/rad。
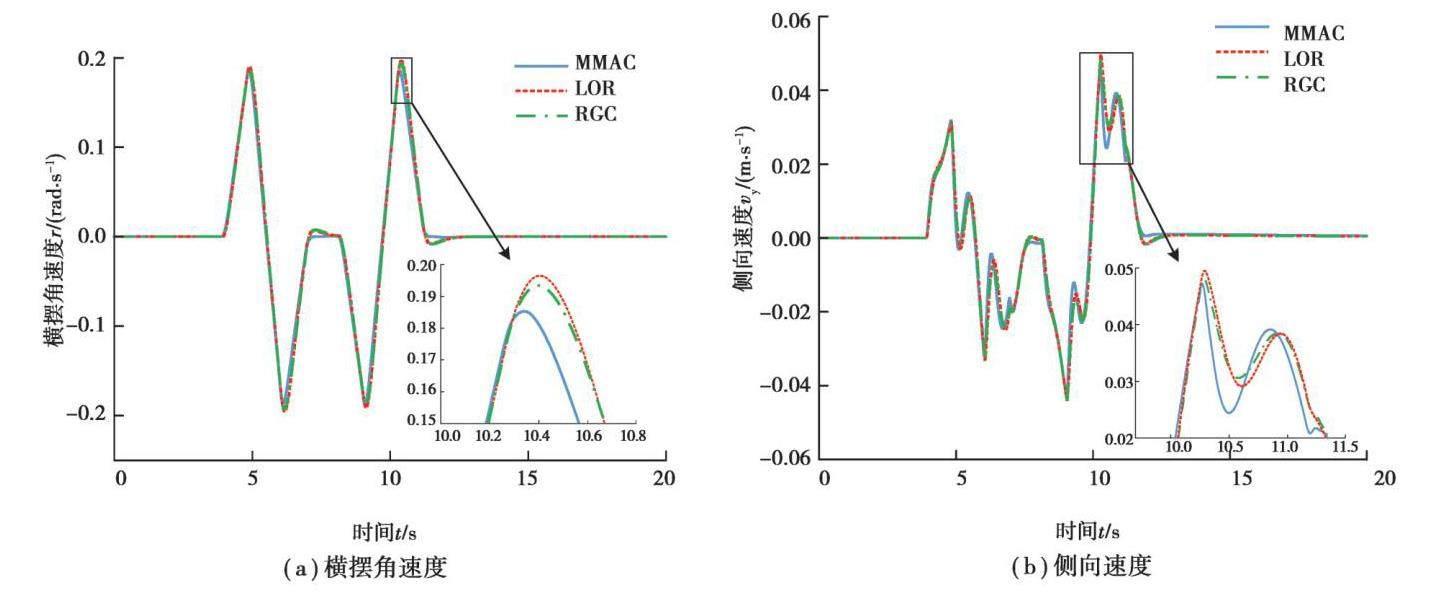
在第1组仿真中,智能汽车在高附着路面(μ=0.85)以60 km/h的速度完成对给定双移线路径的跟踪,其路径跟踪情况如图6所示。从图6(a)中可以看出,虽然3组控制器在高附着路面下都能完成较精确的路径跟踪,但MMAC的偏差明显小于其他2种方法,这也说明即使在高附着路面上,基于理想状况标定出的名义侧偏刚度仍然和汽车面临的实际情况有一定差异。基于名义模型的LQR控制器的跟踪效果略好于鲁棒保性能控制器,这也反映了上文中所提到的鲁棒控制器在正常工况下的保守性,同样的现象也可以从图6(b)中的航向角偏差看出。图6(c)中的全局路径显示,3组控制器都可以很好地完成对给定双移线路径的跟踪,但多模型自适应控制器的完成质量明显好于2组对比控制器。
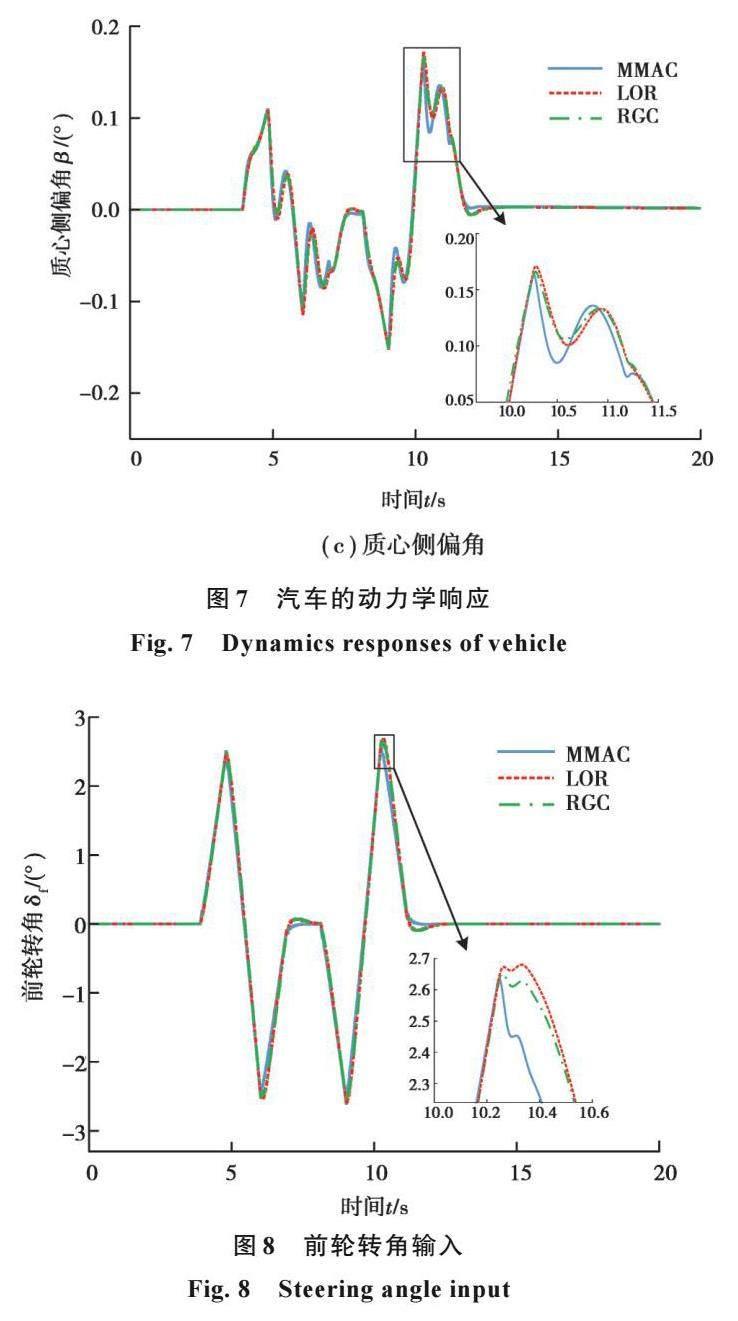
在此工况下,仿真计算得到汽车的动力学响应如图7所示。可以看出,3种控制器的动力学响应基本一致。但是MMAC的侧向速度和质心侧偏角的峰值仍然略小于另2组控制器,这也反映了其在保证汽车的动力学稳定性和可控性上有更强的能力。图8是汽车的前轮转角,从中可知,3组控制器输出的控制量都在合理的范围内。
3.2低附着路面仿真
为了进一步验证所提出的方法,第2组仿真实验中,将路面附着系数调整为0.35,该类附着系数常见于雨雪后的湿滑路面,在这类路面上,轮胎侧偏刚度往往相对其名义值有较大的偏差。在该路面条件下,智能汽车仍以60 km/h的时速完成上述的双移线路径跟踪,以测试控制器的鲁棒性。图9为汽车的路徑跟踪情况,从中可以看出,所提出的控制器在低附着工况下仍然具有最好的跟踪的性能,而此时基于名义模型的LQR控制器的性能已明显不如鲁棒保性能控制器。而且,从图9(b)中可以发现,基于名义模型LQR控制器的航向角偏差在完成双移线第2个换道时出现了严重的超调,这从图9(c)的全局路径中也能看出,相比于多模型自适应控制器和鲁棒保性能控制器,该控制器在经过反复调整后,才消除了变换回原车道后的超调偏差。这些结果表明,在低附着工况下,基于名义模型的控制器开始出现明显的不足,而鲁棒控制和本文中提出的多模型自适应控制方法仍然可以保证较好的控制效果。
对低附着路面工况,仿真计算得到汽车的动力学响应如图10所示。可以发现,多模型自适应控制器和鲁棒保性能控制器在低附着路面上仍然可以较好地保证汽车的动力学性能,而基于名义模型的LQR控制器的动力学响应出现了明显的异常,其各参数在第2次换道时均出现明显的超调和振荡,这对汽车的动力学稳定性十分不利。相似的情况也出现在图11的前轮转角输入中,基于名义模型的LQR控制器的输入在第2次换道一开始就出现了异常的情况,而多模型自适应控制器和鲁棒控制器的输入响应都在合理的范围内,这也进一步验证了所提出方法的优越性。
3.3定量分析
为了更加深入地分析仿真结果,计算了汽车的路径跟踪横向偏差和航向角偏差的均方根值和最大值(表2)以及汽车质心侧偏角的均方根值和最大值(表3)来定量分析控制器的路径跟踪性能和汽车的动力学稳定性,在高附着和低附着路面下的均方根值的相对比值越高,说明控制器的性能保持能力越强。对表中的数据进行定量分析可以看出,基于名义模型的LQR控制器在低附着路面上的性能与高附着路面相比明显下降,而鲁棒保性能控制器(RGC)在低附着路面上的性能与高附着路面比较接近,这也体现了鲁棒控制方法的特点。本研究中提出的多模型自适应控制器(MMAPC),虽然在路面附着变化下的性能保持能力不如鲁棒控制方法,但由于其相比于鲁棒控制方法较低的保守性,在高附着和低附着路面上都取得了最佳的控制效果。
3.4快速原型验证
前面的对比研究分析证明了所提出多模型自适应算法在智能汽车运动控制中的优越性。但是,由于仿真分析的目的是通过对比研究对普通控制方法、鲁棒控制方法及所提出的多模型自适应控制方法在不同路面条件下的特征进行分析,因此所使用的车速不高。为了更加充分地验证所提出的多模型自适应控制器的适用性,本节将在更高的速度下对其进行测试。
实车试验在汽车动力学与控制的相关研究中具有最强的说服力,但是由于中高速工况下智能汽车运动控制和辅助驾驶控制的实车验证较危险及开展试验的相关条件不够成熟,目前对于相关控制策略的实车验证集中在低速工况(0~40 km/h)[19-20]。基于对安全性及设备条件的考虑,已报道的相关研究主要选择硬件在环或快速原型试验台对算法进行初步试验验证[21-22]。因此,为更好地验证所提出算法,选择了快速原型测试的方案对控制算法进行实物在环测试,并对其实时性进行验证。在所设计的方案中,仿真验证的车辆模型仍然使用Carsim中的动力学模型,并在设计控制器的Simulink中加入实时内核。试验测试时,控制信号通过CAN卡和转换器传给电机驱动,进而对转向电机进行实时控制。图12为根据所采用的快速原型测试方案搭建的平台,该平台由计算机、CAN卡、转换器、电机驱动、转向电机和显示界面等组成。
快速原型测试中仍然使用对比分析中采用的双移线路径。设定车速为90 km/h,路面附着系数μ=0.65,该值处于对比研究分析中的高附着条件和低附着条件之间,属于中等附着的路面条件。测试结果如图13所示。
多模型控制算法在速度较高的工况下仍能准确地跟踪参考路径(图13(a)~(c)),其横向偏差和航向角偏差的最大值分别仅为0.133 3 m和2.690 7°。车辆的横摆角速度变化平稳,并且其侧向速度和质心侧偏角都在合理的范围内(图13(d)~(f)),这表明在整个运动过程中,车辆的操纵性和稳定性保持良好。控制器计算出的参考值和CAN卡传递的转向信号(图13(g))能够精确同步。算法的单步求解耗时基本维持在0.001~0.004 s之间(图13(h)),远小于所设置的采样时间0.01 s,证明了所提出自适应算法求解的实时性。对比研究分析和快速原型试验都表明所提出的多模型自适应算法在智能汽车运动控制中能够很好地处理当前各种控制算法在精确性与鲁棒性之间的两难问题。
为进一步论述所提出的控制器在高速工况下的性能,在快速原型验证的工况条件下对MMAC、LQR和RGC这3组控制器进行对比分析(图14)。需要说明的是,由于本研究中所选择的双移线路径曲率较大,在速度较高时,若附着较低,很容易超越汽车的物理附着极限。快速原型验证中选择的工况已经接近物理附着极限,故该工况可以充分证明所提出的方法在高速下的性能。可以看出在高速工况下,3组控制器都能够完成轨迹跟踪的控制目标,而MMAC控制的效果明显好于LQR和RGC。值得一提的是,LQR控制和RGC控制都是比较有代表性的控制算法,在自动驾驶汽车轨迹跟踪控制的研究中已经有了很多应用,其有效性已经得到了广泛的认同,通过与这二者进行对比,多模型自适应算法MMAC的有效性和优越性都得到了充分证明。
4结 论
1) 针对智能汽车路径跟踪控制中轮胎侧偏刚度摄动导致的模型不确定性问题,提出了一种不同于传统鲁棒控制方法的多模型自适应控制方法。
2) 研究证明,所提出的多模型自适应路径跟踪控制器在不同路面附着条件下都能保证良好的性能。在高附着路面上可以实现最精确的路径跟踪控制,而在低附着路面上对模型不确定性的控制问题也具有良好的鲁棒性。
3) 在对比研究分析的基础上进行了快速原型试验,进一步验证了多模型自适应算法的有效性和适用性。結果显示多模型自适应算法可以很好地保证实时性,具有良好的工程应用潜力。
4) 多模型自适应控制方法在保证鲁棒性的同时克服了传统的鲁棒控制方法保守性较强的问题,无需在控制性能与鲁棒性能之间进行妥协,为不确定性系统的控制器设计引入了新的思路。
后续的研究将在自适应算法中把车辆信号的噪声考虑进来,研究在信号噪声的干扰下如何保证控制器的精确性和鲁棒性。
参考文献
[1] 《中国公路学报》编辑部. 中国汽车工程学术研究综述·2017[J]. 中国公路学报, 2017, 30(6): 1-197.
Editorial Department of China Journal of Highway and Transport. Review on Chinas automotive engineering research progress: 2017[J]. China Journal of Highway and Transport, 2017, 30(6): 1-197. (in Chinese)
[2] Levinson J, Askeland J, Becker J, et al. Towards fully autonomous driving: systems and algorithms[C]//2011 IEEE Intelligent Vehicles Symposium (IV), June 5-9, 2011, Baden-Baden, Germany. IEEE, 2011: 163-168.
[3] Marino R, Scalzi S, Netto M. Nested PID steering control for lane keeping in autonomous vehicles[J]. Control Engineering Practice, 2011, 19(12): 1459-1467.
[4] 汪偉, 赵又群, 许健雄, 等. 基于模糊控制的汽车路径跟踪研究[J]. 中国机械工程, 2014, 25(18): 2532-2538.
Wang W, Zhao Y Q, Xu J X, et al. Research on vehicle path tracking based on fuzzy control[J]. China Mechanical Engineering, 2014, 25(18): 2532-2538. (in Chinese)
[5] Hu C, Qin Y C, Cao H T, et al. Lane keeping of autonomous vehicles based on differential steering with adaptive multivariable super-twisting control[J]. Mechanical Systems and Signal Processing, 2019, 125: 330-346.
[6] 郭应时, 蒋拯民, 白艳, 等. 无人驾驶汽车路径跟踪控制方法拟人程度研究[J]. 中国公路学报, 2018, 31(8): 189-196.
Guo Y S, Jiang Z M, Bai Y, et al. Investigation of humanoid level of path tracking methods based on autonomous vehicles[J]. China Journal of Highway and Transport, 2018, 31(8): 189-196. (in Chinese)
[7] 汪选要, 程义, 程煜, 等. 低附着系数路面车道保持模型预测控制及汽车稳定性控制[J]. 中国机械工程, 2019, 30(9): 1018-1025.
Wang X Y, Cheng Y, Cheng Y, et al. Lane keeping model prediction control and vehicle stability control on low adhesion coefficient roads[J]. China Mechanical Engineering, 2019, 30(9): 1018-1025. (in Chinese)
[8] Ji J, Khajepour A, Melek W W, et al. Path planning and tracking for vehicle collision avoidance based on model predictive control with multiconstraints[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 952-964.
[9] 李军, 唐爽, 黄志祥, 等. 融合稳定性的高速无人驾驶车辆纵横向协调控制方法[J]. 交通运输工程学报, 2020, 20(2): 205-218.
Li J, Tang S, Huang Z X, et al. A coordinated control method for high speed unmanned vehicle with integrated stability[J]. Journal of Traffic and Transportation Engineering, 2020, 20(2): 205-218. (in Chinese)
[10] 李亮, 贾钢, 宋健, 等. 汽车动力学稳定性控制研究进展[J]. 机械工程学报, 2013, 49(24): 95-107.
Li L, Jia G, Song J, et al. Progress on vehicle dynamics stability control system[J]. Journal of Mechanical Engineering, 2013, 49(24): 95-107. (in Chinese)
[11] 黄彩霞, 雷飞, 胡林, 等. 轮毂电机驱动汽车区域极点配置横向稳定性控制[J]. 汽车工程, 2019, 41(8): 905-914.
Huang C X, Lei F, Hu L, et al. Lateral stability control based on regional pole placement of in-wheel-motored electric vehicle[J]. Automotive Engineering, 2019, 41(8): 905-914. (in Chinese)
[12] Wang J X, Dai M M, Yin G D, et al. Output-feedback robust control for vehicle path tracking considering different human drivers characteristics[J]. Mechatronics, 2018, 50: 402-412.
[13] Guo J H, Luo Y G, Li K Q. Robust gain-scheduling automatic steering control of unmanned ground vehicles under velocity-varying motion[J]. Vehicle System Dynamics, 2019, 57(4): 595-616.
[14] Wang R R, Jing H, Hu C, et al. RobustH∞path following control for autonomous ground vehicles with delay and data dropout[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(7): 2042-2050.
[15] Guo J H, Wang J, Hu P, et al. Robust guaranteed-cost path-following control for autonomous vehicles on unstructured roads[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2018, 232(7): 896-908.
[16] 刘瑞, 朱西产, 李霖. 紧急变道工况鲁棒性车辆轨迹跟踪策略[J]. 同济大学学报(自然科学版), 2017, 45(11): 1659-1663.
Liu R, Zhu X C, Li L. Robust trajectory following strategy during emergency lane-change condition[J]. Journal of Tongji University (Natural Science), 2017, 45(11): 1659-1663. (in Chinese)
[17] Zengin H, Zengin N, Fidan B, et al. Blending based multiple-model adaptive control of multivariable systems with application to lateral vehicle motion control[J]. European Journal of Control, 2021, 58: 1-10.
[18] Lemos J M, Neves-Silva R, Igreja J M. Solar energy collector systems[M]//Adaptive control of solar energy collector systems. Cham: Springer International Publishing, 2014: 1-25.
[19] 蔡英凤, 臧勇, 孙晓强, 等. 基于可拓切换控制方法的智能车辆车道保持系统研究[J]. 中国公路学报, 2019, 32(6): 43-52.
Cai Y F, Zang Y, Sun X Q, et al. Research on intelligent vehicle lane keeping system based on extension switch control method[J]. China Journal of Highway and Transport, 2019, 32(6): 43-52. (in Chinese)
[20] 张炳力, 李子龙, 沈干, 等. 基于模糊神经网络的智能汽车轨迹跟踪研究[J]. 汽车工程, 2019, 41(8): 953-959.
Zhang B L, Li Z L, Shen G, et al. A research on path tracking of intelligent vehicle based on fuzzy neural network[J]. Automotive Engineering, 2019, 41(8): 953-959. (in Chinese)
[21] Cheng S, Li L, Mei M M, et al. Multiple-objective adaptive cruise control system integrated with DYC[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 4550-4559.
[22] Zhang B H, Lu S B. Fault-tolerant control for four-wheel independent actuated electric vehicle using feedback linearization and cooperative game theory[J]. Control Engineering Practice, 2020, 101: 104510.
(編辑 罗敏)
