运用数学建模实现料堆三维模型实时更新方法的研究
2024-05-22国能粤电台山发电有限公司张云武畅学辉金太山欧国平欧阳海峰刘文泉刘海军孟立军
国能粤电台山发电有限公司 张云武 畅学辉 金太山 欧国平 欧阳海峰 刘文泉 刘海军 孟立军
在现有针对圆形料场的盘煤方案中,均使用的是搭载云台的盘煤仪[1]。综合考虑成本及施工难度,现将其固定均匀吊装在圆形煤场穹顶龙骨上,具体设置的数量根据煤场大小而定[2]。经分析,通过堆取料机的基础物理数据的测量采集,和对已有绝对值编码器数据的二次利用[3],完成精准数据建模,实现跟随堆取料作业的盘煤数据实时更新,进而为操作员提供可实时更新的煤堆三维模型。
1 圆形煤场堆取料作业数学建模方法
如图1所示,根据堆取料机、煤堆的物理特性,将其分别抽象成物理模型[4],并依据各自运行特征分别对堆料、取料过程进行建模。
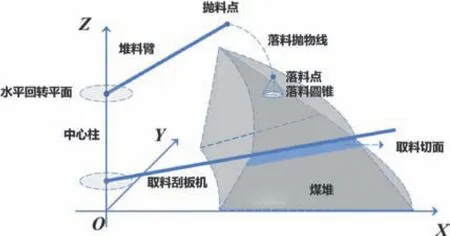
图1 抽象物理建模示意图
1.1 堆料建模
如图2所示,煤从堆料臂出来时并非垂直落下,而是按照一定角度θ,以及初速度v0做抛物状从A点下落至B 点。A 点为抛料点,B 点为落料点,落料点下方圆锥为自然形成的料堆形状。
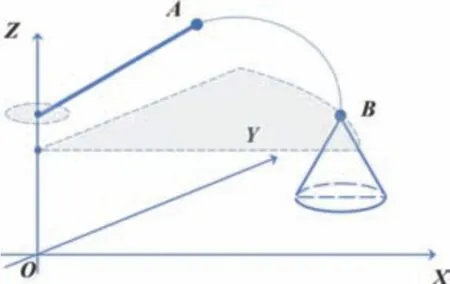
图2 堆料三维示意图
1.1.1 抛料点位置计算
抛出点计算可通过堆料臂参数以及当俯仰、回转数值进行计算,所需要参数有:堆料臂在主轴连接处的水平高度ha、大臂长度l、俯仰角θ、回转角α。如图3所示。
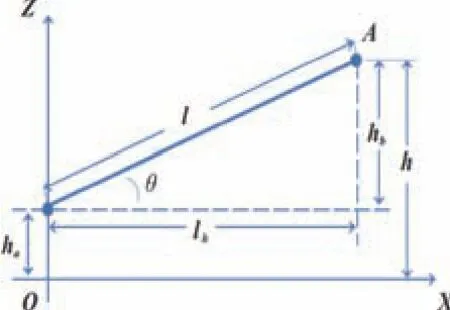
图3 抛料点计算建模(侧视)
根据图4,通过大臂长度与俯仰角计算出大臂在水平面上的投影长度lh、大臂抬升高度hb及抛出点的高度h,计算公式如下:lh=l·cosθ,hb=l·sinθ,h=ha+hb。根据图4,通过回转角计算出抛出点的X 轴、Y 轴坐标。计算公式如下:xa=lh·cosa,ya=lh·sina。依上述公式算得抛出点A 坐标为:(xa,ya,h)。
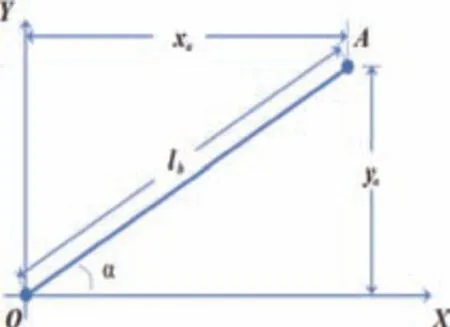
图4 抛料点计算建模(俯视)
1.1.2 落料点计算
落料点计算可通过斗轮机设计参数以及俯仰、回转数值进行计算,所需要参数有:抛出点高度h、抛出点X 轴坐标、抛出点Y 轴坐标、回转角a、抛出点初速度(皮带运行速度)v0、重力加速度g等常数。如图5所示。
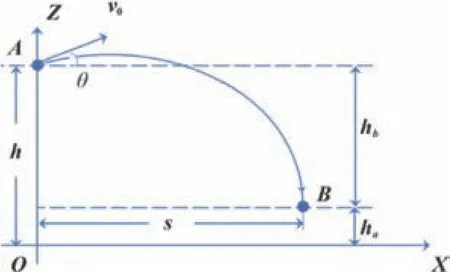
图5 落料点计算建模(侧视)图
通过斜抛运动公式计算出从抛出点A到落料点B之间的距离s,计算公式如下:其中,hb通过料高雷达数值反馈数据值及其安装高度、距离抛料点高度计算求得。
如图6所示,从俯视角度,将抛出点A与落料点B投影到X、Y平面后,hb点相当于Ah点沿大臂回转方向向外侧移动了s距离。通过三角函数计算可得出B点的X轴Y 轴坐标,计算公式如下:xs=s·cosa,xb=xa+xs,ys=s·sina,yb=ya+ys,ha=h-hb。综上,算得落料点B 坐标为:(xb,yb,ha)。
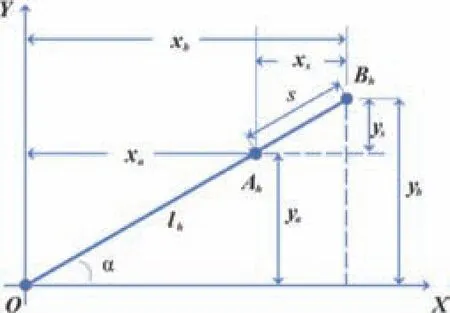
图6 落料点计算建模(俯视)图
1.1.3 自然堆料圆锥表面坐标计算
在落料点B 进行堆煤时,煤块按照堆积角β 向四周扩散,并堆成圆锥体形状,如图7所示。
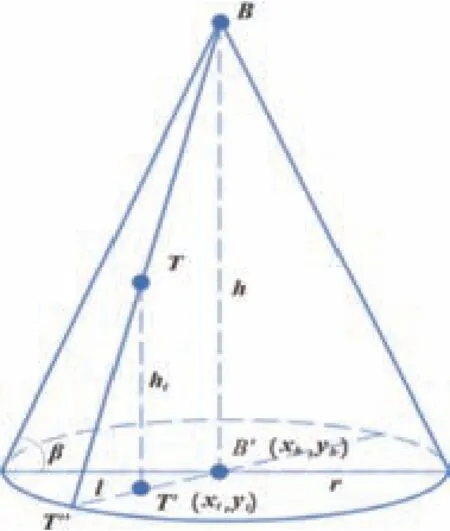
图7 圆锥表面坐标计算建模图
要计算煤场的三维点云,可以将煤场X、Y 平面进行栅格化,对每个x,y坐标求其对应的高度z值即可。任意选取圆锥斜面上点T,其在圆锥底面的投影点T'与T的高度ht即为理论纵坐标。如图7可知,△TT'T''与△BB'T''为相似三角形,圆锥高度h通过上面的公式已经求得,只需要求出底面半径r、线段T'T''的长度l,就可通过相似三角形求得T点高度ht,计算公式如下:r=h·cotβ,ht=(r-l)/r·h,
1.2 取料建模
刮板机在取料过程中,刮板通过俯仰机构控制与煤面接触,刮板底部深入煤层内部,通过纵向运动取走与刮板截面相接触的煤[5],如图8所示。PQ为刮板机轴心所在的直线,直线下方阴影为刮板底部深入煤层取煤的横断面。
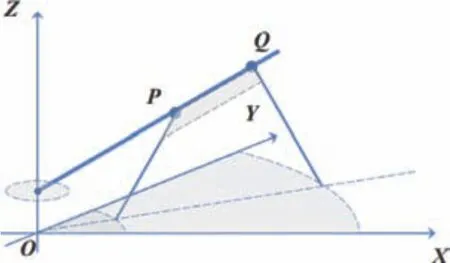
图8 取料数学建模三维示意图
1.2.1 水平回转侧视截面点云边界计算
如图9所示,PQ所在的直线ls即为刮板机建模中轴线,P1Q1所在的直线ls'平行于ls,纵向垂直距离为d。故在三维点数据中心,随着刮板机的水平回转,将直线ls'以上的料堆点云数据减掉,即可更新实时料堆点云数据,公式如下。
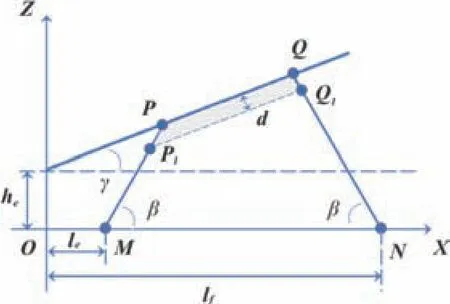
图9 取料数学建模(侧视)图
PQ所在直线ls解析式:y1=tanγ·x1+he(1);P1Q1所在直线ls'的解析式:y2=tanγ·x2+(he-d/cosγ) (2),判断点云数据集中的任一点H(xH,yH,zH)是否在如图所示的随机阴影区域内,计算方法如下。
将xH代入式(2)求得y值,如果所得y 值大于等于yH,则该数据进入待操作区,等待下一步验证;反之则保留该点云数据。同时,利用上述数据计算PM及QN所在的直线解析式,公式如下。
PM所在直线解析式:y3=tanβ·x3-tanβ·le(3);QN所在直线解析式:y4=tanβ·x4-tanβ·lf(4),联立式(2)、式(3)、式(4)三式只需求得直线ls'位于P1Q1之间点的横坐标范围,可以得到P1点横坐标为(tanβ·le+he-d/cosγ)/(tanβ-tanγ),Q1点横坐标为(d/cosγ-tanβ·lf-he)/(tanγ+tanβ)。
1.2.2 水平回转俯视截面点云边界计算
如图10所示。其中,PQ为刮板机水平回转时的一侧到边位置,P2Q2为另一侧到边位置。
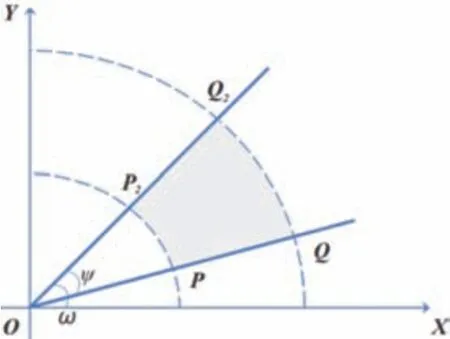
图10 取料数学建模(俯视)图
通过上一步计算可知,以OP为半径的圆,半径r1=(tanβ·le+he-d/cosγ)/(tanβ-tanγ); 以OQ为半径的圆,半径为r2=(d/cosγ-tanβ·lf-he)/(tanγ+tanβ)。
判断点云数据集中的任一点H(xh,yh,zh)是否在如图所示的随机阴影区域,判断方式如下。
首先,利用H点的坐标计算其与Z轴的距离再计算经过H点和原点的直线斜率kh=yh/xh。
第二步,遍历在步骤1.2.1中的待操作区中的点云数据集做上述运算,如果且tanω≤yh/xh≤tanφ,则将该点云数据去除。
1.3 交叉重叠算法
经过上述数学建模遍历出的点云数据,在Z轴上需对坐标进行交叉重叠算法处理。因已经将煤场栅格化[6],所以只需将X轴和Y轴重叠点的Z轴坐标进行加减法计算,即可得到实时点云的Z轴新坐标。
2 当前成果与后期展望
方案精准度验证:以取料作业数据为例,采集从第1层到第5层每一层取完后的剩余体积。原始体积记作V0,则每取一层煤后,高精度的便携式盘煤仪计算所得的体积记为Vn,数学建模法计算所得的体积记为V'n,统计剩余体积百分比k0-n=Vn/V0×100%,形成如图11所示对比图。
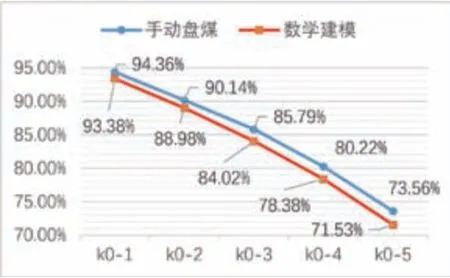
图11 单次作业手动盘煤与数学建模盘煤精准度对比图
综合50次作业数据分析,首先对基准体积值Vn为每层剩余体积两种方式取得的体积值计算平均值,进而求得所对应的偏差量均值每层偏差率形成如图12所示的偏差预测曲线。
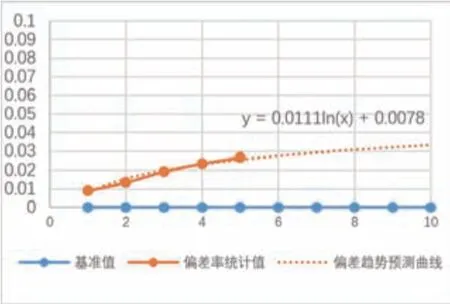
图12 偏差预测曲线图
通过统计数据拟合曲线公式可知,取料建模的精准度在回转至10层时约为96.66%。
