基于模态分析法的钢组合结构支座选取分析

魏国庆，孟 媛，王占魁

(1.青岛市公路事业发展中心,山东 青岛 266071;2.长安大学 建筑工程学院,陕西 西安 710061;3.青岛市招标中心,山东 青岛 266072;4.潍坊市白浪河水库运营维护中心,山东 潍坊 261052)

大跨度空间结构是衡量一个国家建筑业发展水平的重要评价标准，其设计建造水平体现了一个国家的综合国力[1]。20世纪70年代后，鉴于轻质高强材料的发展，大跨度空间结构在大型公共建筑中得到广泛应用[2-3]。大悬臂钢桁架的网架结构作为一种大跨空间结构的混合结构，在设计建造中需考虑多种荷载作用尤其是地震作用的影响，地震时由于结构受到动力作用的影响产生强迫振动。地震反应是一种动力反应，其大小与自振周期、振型和阻尼等结构自身动力特性有关。而结构抗震性能研究主要通过对动荷载的响应大小，确定结构的承载能力、变形能力和动力学特性，为结构的抗震性能设计提供重要依据[4-5]。

模态分析作为一种动力特性分析方法，能够判断空间结构自振特性等重要参数，是结构动力分析和获得结构动力响应参数的关键。通过模态分析提高结构的自振频率，为结构的动力特性优化设计提供依据，从而改善结构的抗震性能[6-7]。随着对结构抗震和动力性能深入研究，发现地震动具有明显的随机性和非平稳特征[8]。因而对结构的抗震性能，尤其是大跨度空间结构的动力特性研究极为重要[9-10]。研究发现模态分析能够对结构刚度大小和质量分布做出定性判断。通过选取合适的支座模型，进而分析出结构的抗震性能。SAP2000作为有限元分析软件，具有集成化的使用界面、完备的设计工具以及强大的分析功能等优点[11-12]，可以完成对阻尼器一类的耗能装置进行整体建模分析。

本文利用SAP2000对西安某体育馆进行建模研究，考虑刚性铰接支座与弹性支座两种模型，通过Ritz向量法分别对两种模型进行模态分析，分析不同模型对结构周期、振型的影响，进而得出不同支座类型对结构动力特性及抗震性能的影响，选择出混凝土框架柱与网架结构连接部分的最佳支座模型，以期可为今后类似工程设计提供参考意义。

1 工程概况

1.1 工程概况

工程项目为西安某体育馆,地下1层、地上两层,建筑面积为15 233.80 m2。下部是混凝土框架结构,上部为大悬臂钢桁架的架结构,钢结构屋盖采用网架与悬挑桁架相结合的矩形平面结构形式,正放四角锥的网架形式,结构采用螺栓球连接。平面结构长度为84.00 m,宽度为56.7 m,高度为20.95 m,网架部分长度为71.10 m,宽度为55.40 m，厚度为2.00～3.50 m，上弦杆件从屋盖边缘到屋脊之间坡度为3°，采用上弦柱点支撑。桁架部分采用平行弦桁架，长度为55.4 m，宽度为9.55 m，桁架厚度为0.7 m，由15榀主桁架及5榀次桁架组成，桁架采用圆钢管及相贯节点。

下部混凝土框架结构与钢结构屋盖共有杆件数5 742根，框架结构柱、梁及板的混凝土强度等级均为C30，泊松比取0.2，弹性模量取30 kN/mm2，剪切模量取12.5 kN/mm2。上部结构嵌固部位为地下室顶板，主筋采用HRB400钢筋，箍筋采用HRB400钢筋。桁架和网架结构均采用材料为Q345B无缝钢管，泊松比取0.3，网架钢结构杆件之间为铰接，框架柱下部节点为刚接。

1.2 模型建立

采用SAP 2000软件建立大跨拱形空间桁架的有限元模型，梁、柱及圆钢管均用框架单元模拟，板采用壳单元模拟，节点数为2 820，采用Rubber Isolator单元模拟，共计34个。建模步骤：

(1)根据体育馆设计图建立模型坐标系、轴网、材料以及截面属性。

(2)依次建立柱、梁、板、弹簧支座、网架下弦、上弦、腹杆以及桁架部分的模型。

(3)利用Rubber Isolator单元模拟，计算得出支座模型的水平刚度、竖向刚度，进行连接单元的连接属性数据定义。

(4)确定荷载。杆件自重由系统导出，框架根据《建筑结构荷载规范》(GB 50009—2012)[13]的要求，确定为活荷载，通过计算得到墙体恒荷载，同时将定义厚度为零的壳作为屋面板自重及外荷载进行施加，并以双向板的形式将面荷载传递到杆件节点。

模型一采用直接铰接的方法建立铰接支座模型，模型二连接采用弹性支座的形式建立模型，体育馆模型及大悬臂桁架的网架结构模型如图1、2所示。

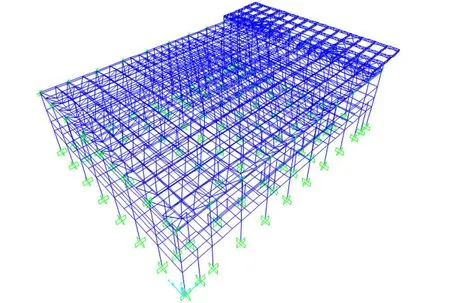
图1 体育馆模型

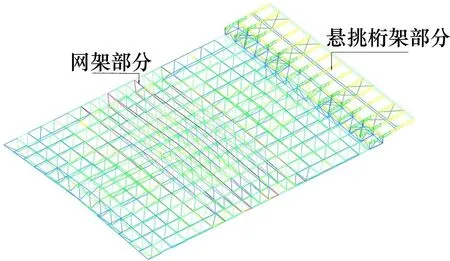
图2 具有大悬臂桁架的网架结构模型

2 模态分析

2.1 基本理论

模型利用SAP2000进行模态分析时，考虑到子空间迭代法相对稳定，Ritz向量法考虑了动力荷载的空间分布，其计算量更少且更准确，因此取前40阶振型进行模态分析，求得结构的自振频率及振型[14-16]

在结构动力分析中[17]，结构动力响应的求解是基于质量系统的动力平衡方程来完成的，多自由度集中质量体系的动力平衡方程如下。

Ft(t)+FD(t)+Fs(t)=F(t)

式中：FI(t)为用在节点质量上的惯性力向量，kN；FD(t)为粘滞阻尼力向量或者能量耗散力向量，kN；FS(t)为结构承担的内力向量，kN；F(t)为外部施加的荷载向量，kN。

2.2 模态分析结果

支座模型的前40阶自振周期和频率模态分析结果如表1所示，支座模型自振周期曲线如图3所示，振型-频率分布曲线如图4所示。

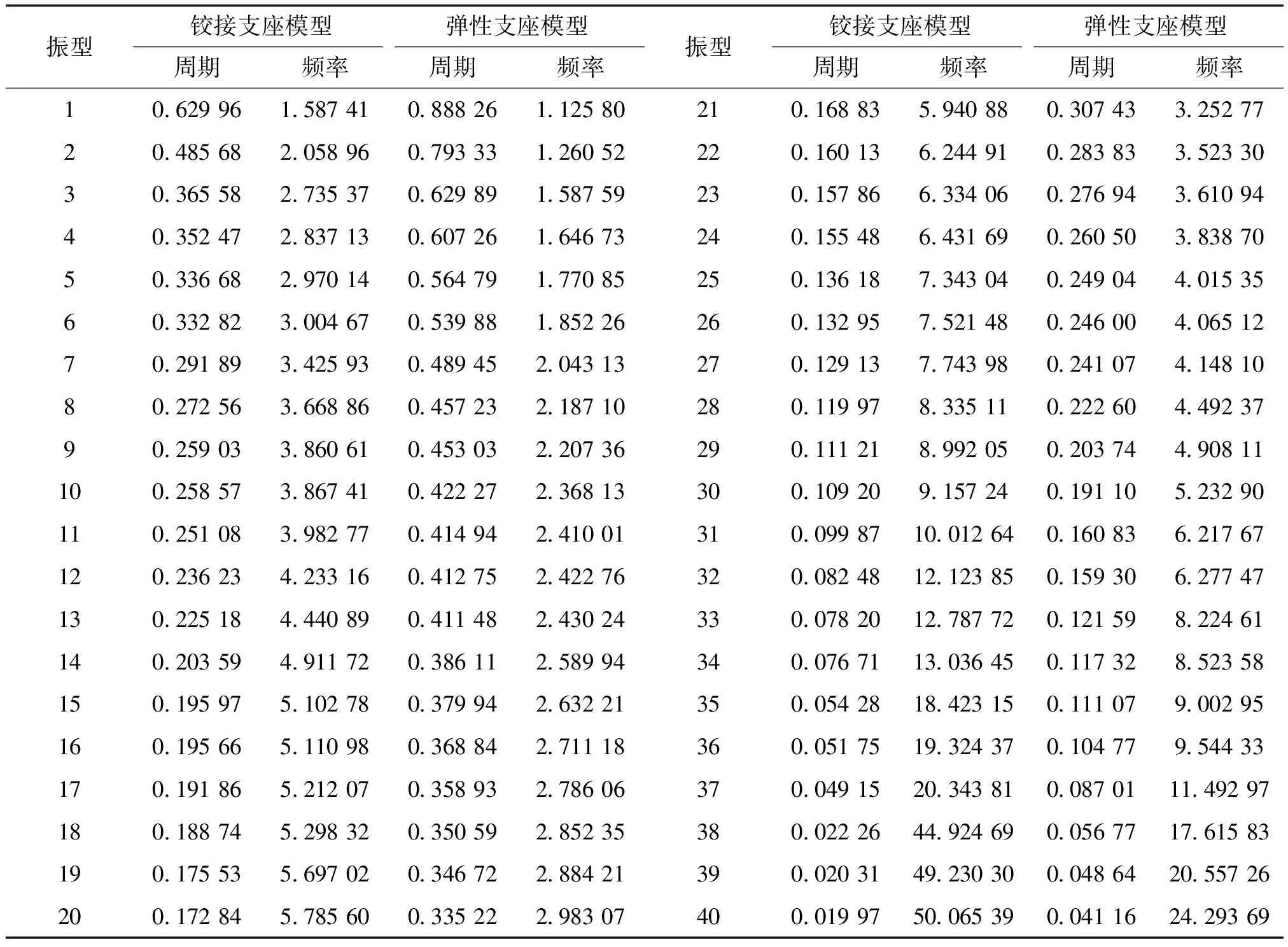
表1 铰接支座和弹性支座模型的前40阶自振周期和频率

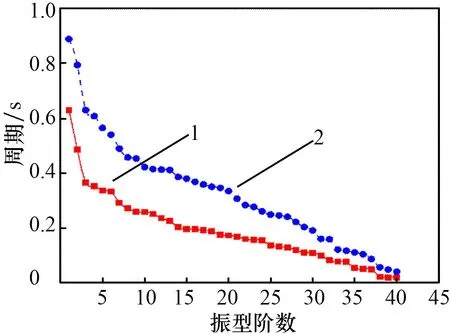
1—固定铰支座模型；2—弹性支座模型

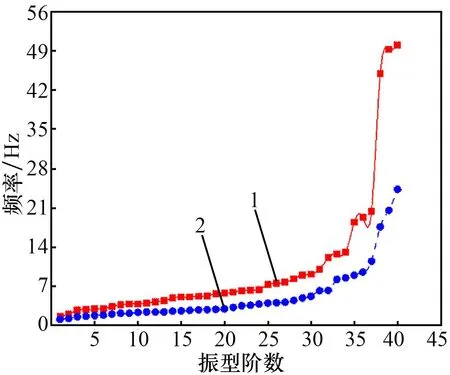
1—固定铰支座模型；2—弹性支座模型

通过分析表1的数据可知，固定铰支座模型与弹性支座模型两者的自振频率相差较大。相较于弹性支座模型，固定铰支座模型第1阶自振频率由1.587 41降低到1.125 8，减小了41.0%；第10阶自振频率由3.867 41降低到2.368 13，减小了63.31%；第20阶自振频率由5.785 6降低到2.983 07，减小了93.95%；第20阶自振频率由5.785 6降低到2.983 07，减小了93.95%；第40阶自振频率由50.065 39降低24.293 69，减小了106.08%。从图3、4可以看出，相较于固定铰支座模型，弹性支座模型振型-频率曲线更为平缓，主要因为弹性支座模型整体结构柔性大，水平方向刚度小；而固定铰支座模型结构相反，使得固定铰支座模型的结构自振周期曲线下降迅速，周期更小。

由此可以看出，相较于弹性支座模型，固定铰支座模型误差很大，因此结构选取弹性支座模型。对该结构进行整体建模，由于结构形式较为复杂，仅就上部网架结构进行模态分析展示，结构振型如图5、6所示。

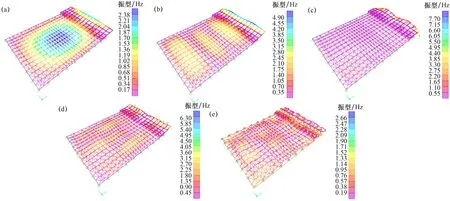
(a)铰接支座模型第1阶振型;(b)铰接支座模型第10阶振型;(c)铰接支座模型第20阶振型;(d)铰接支座模型第30阶振型;(e)铰接支座模型第40阶振型

(a)弹性支座模型第1阶振型;(b)弹性支座模型第10阶振型 ;(c)弹性支座模型第20阶振型;(d)弹性支座模型第30阶振型(e)弹性支座模型第40阶振型

取弹性支座模型前40阶振型结构的质量参与系数进行分析，其中，UX、UY、UZ、RZ分别表示结构X、Y、Z、RZ方向的振型参与质量系数，SumUX、SumUY、SumUZ分别表示结构X、Y、Z方向振型参与质量系数之和，如表2所示。

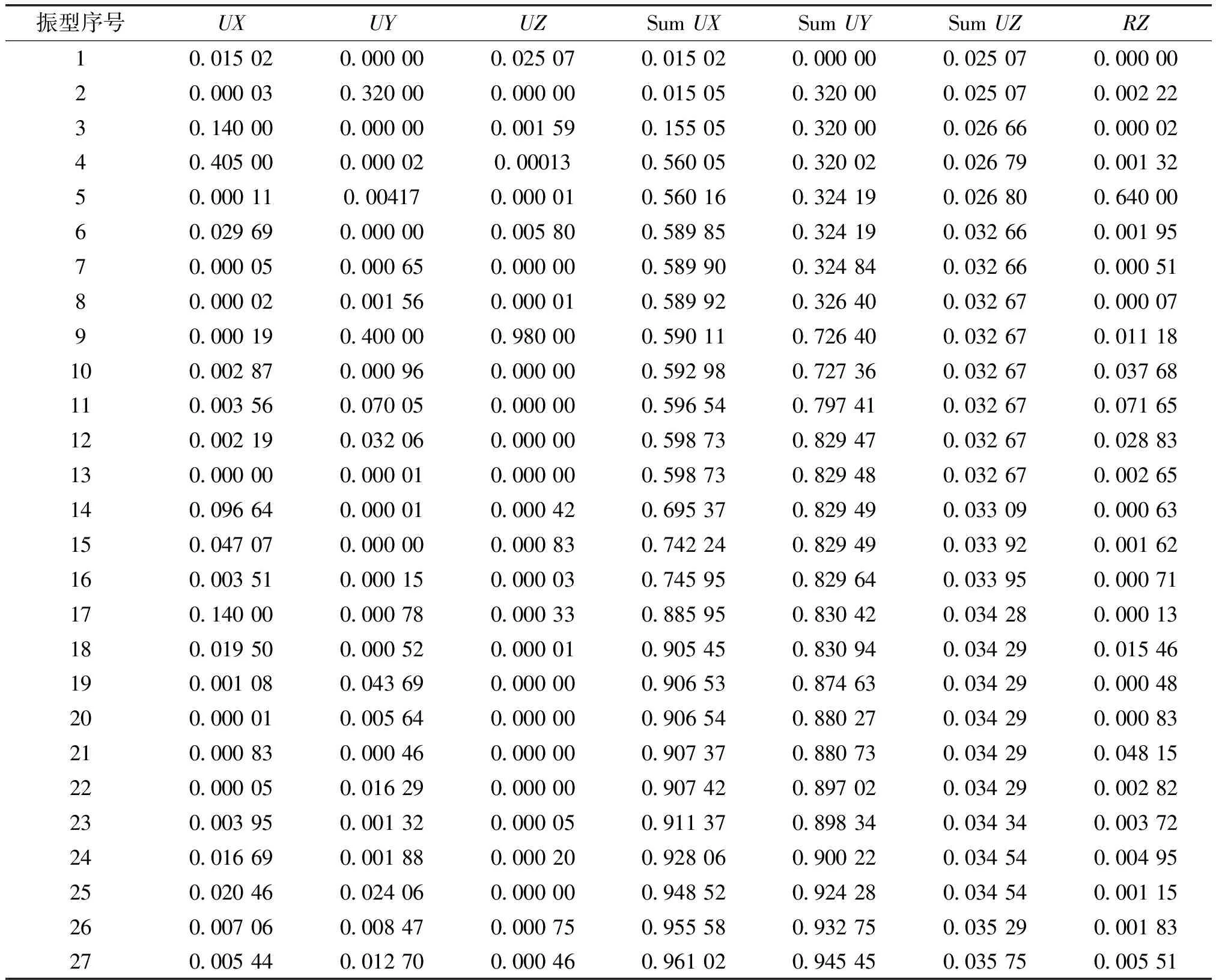
表2 弹性支座模型前40阶质量参与系数

通过图5及表2可知，弹性支座模型模态振型整体刚度分布均匀，属于整体振动。同时通过对结构的前40阶振型分析发现：振型一时，UZ=0.025 07>UX=0.015 02,说明结构的第一振型以Z方向的竖向振动为主;振型十时,UX=0.002 87>UY=0.000 96,说明结构的第10振型是以X方向的平动为主；振型为20时，UY=0.005 64>UX=0.000 01，说明结构的第3振型是以Y方向的平动为主；振型为30时,UX=0.005 02>UZ=0.000 13，说明结构的第1振型以X方向的竖向振动为主；振型为40时，UZ=0.036>UZ=0.000 02,说明结构的第1振型以Z方向的竖向振动为主，符合规范要求。

3 结 论

本文通过有限元软件SAP2000对大悬臂桁架与网架组合结构进行模态分析，研究刚性铰接支座与弹性支座两种模型下对结构周期、振型的影响。结果表明，弹性支座模型整体结构柔性大，水平方向刚度小且刚度分布均匀，整体性更好，在地震作用下可以吸收地震能量，充当隔振支座的作用，在地震荷载作用下整体结构抗震性能优于刚性铰接支座，因此选择弹性支座模型作为混凝土框架柱与网架结构连接部分的最佳支座形式[18]。