经验模态分解-图神经网络算法预测农产品价格

赖玉莲 马琳娟 张延林

文章編号：1671-3559（2024）03-0356-06DOI：10.13349/j.cnki.jdxbn.20240312.003

摘要： 为了提高图神经网络算法对农产品价格预测精度， 采用经验模态分解法按时间片轮转抽取农产品历史价格信号， 以便对历史价格信号进行特征提取； 将原始价格信号分解成多个本征模态函数及残余项， 并根据本征模态函数构建样本特征； 根据得到的样本特征构建价格预测图结构， 将图结构输出的特征信号通过图神经网络的过渡函数和预测函数， 通过不断减小损失值输出农产品价格预测结果。 结果表明， 经验模态分解可以对原始农产品价格信号的本征模态函数分量进行有效分解和提取， 从而使经验模态分解-图神经网络算法的农产品价格预测平均绝对误差减小71.4%； 相比于其他类型的预测算法， 经验模态分解-图神经网络算法对4类农产品价格预测的平均绝对误差更小， 最大值仅为2.465。

关键词： 农产品价格预测； 图神经网络； 经验模态分解； 本征模态函数

中图分类号： TP391

文献标志码： A

开放科学识别码（OSID码）：

Agricultural Product Price Prediction Based on Empirical

Mode Decomposition and Graph Neural Network Algorithm

LAI Yulian1， MA Linjuan2， ZHANG Yanlin3

（1. School of Business Administration，Guangzhou Institute of Science and Technology，Guangzhou 510540， Guangdong， China;

2. School of Computer Science and Technology， Beijing Institute of Technology， Beijing 100081， China;

3. School of Management， Guangdong University of Technology， Guangzhou 510006， Guangdong， China）

Abstract： To improve the accuracy of agricultural product price prediced by using graph neural network （GNN） algorithm， empirical mode decomposition （EMD） method was used to extract the historical price signals of agricultural pro-ducts in turn according to time slices， so as to extract the characteristics of the historical price signals. The original price signal was decomposed into several instrinsic mode functions and residual terms， and the sample characteristics were constructed according to the instrinsic mode functions. According to the obtained sample characteristics， the graph structure was constructed， and the characteristic signals output from the graph structure pass through the transition function and prediction function of GNN algorithm， and the agricultural product price prediction results were output by continuously reducing the loss value. The results show that EMD can effectively decompose and extract the intrinsic mode function components of the original agricultural product price signals， thus the average absolute error of agricultural product price predicted by using EMD-GNN algorithm is reduced by 71.4%. Compared with other types of forecasting algorithms， the average absolute error of EMD-GNN algorithm for the price prediction of 4 types of agriculture products is smaller， and the maximum value is only 2.465.

Keywords： price prediction of agricultural products; graph neural network; empirical mode decomposition; intrinsic mode function

收稿日期： 2023-01-15          网络首发时间：2024-03-13T10：19：23

基金项目： 国家自然科学基金项目（72272039）

第一作者简介： 赖玉莲（1981—），女，广东梅州人。讲师，硕士，研究方向为数据分析、 农业科技、 产品分析。E-mail： lotuser101@126.com。

通信作者简介： 张延林（1974—），男，河南洛阳人。副教授，博士，研究方向为大数据与人工智能、数字技术。E-mail： forestgdut@163.com。

网络首发地址： https：//link.cnki.net/urlid/37.1378.N.20240312.1702.006

农产品价格预测作为大数据技术在农业中的一项重要应用， 有效提升了农产品生产计划的预见性和合理性［1］， 也影响了广大居民消费习惯， 更重要的是， 农产品价格的平稳运行关乎民生问题。 通过对一个城市的多个农贸市场的样本特征及天气物流等数据进行有效分析， 可以实现该城市的农产品价格预测。 通过价格预测， 一方面为农业种植者的种植规划方案提供策略支持， 减少资源浪费； 另一方面为农产品消费者提供价格预测， 提升消费预见性。 由于影响农产品价格指标要素较多且受外部环境影响较大， 而且采集的历史价格信号容易掺杂噪声， 因此要根据这些特征获得较高的价格预测精度并不简单。

当前主流的预测算法是支持向量机和各种神经网络算法。 为了进一步增强算法对不同农产品价格预测的适用性， 研究者大多对上述2种算法进行改进。 在较新的农产品价格预测研究文献中， 刘合兵等［2］采用极限学习机（extreme learning machine， ELM）模型进行农产品价格预测， 在历史价格信号输入ELM模型之前， 采用经验模态分解（empirical mode decomposition， EMD）法进行历史价格信号分解， 增强历史价格特征数据提取的有效性， 从而提高ELM的预测精度。 王新武等［3］将自回归神经网络算法用于农产品价格预测， 也采用了EMD法进行历史价格信号分解， 实现农产品价格预测。 虽然采用EMD进行原始信号特征提取可以有效地进行特征数据分解， 但是预测模型的精度还有提升空间。

近期， 不少研究者尝试采用先进的图神经网络算法（graph neural network， GNN）实现各种场景的预测需求，如水质量预测［4］、 轴承故障预测［5］等，均取得了比现有机器学习模型更好的性能。

本文中采用GNN的图结构进行农产品价格预测特征训练， 并借助EMD法进行特征提取， 将EMD-GNN算法用于农产品价格预测。

1  EMD

EMD能够实现连续信号的多个振荡函数分解，将复杂且不平稳的时间信号进行有效处理，把它们分解成若干简单的时间信号。EMD处理后得到的分解结果主要由多个本征模态函数（intrinsic mode function，IMF）以及不能进行分解的残余信号构成。

EMD的核心就是不断地从原始时间信号中对照IMF要求进行筛选［6］，将原始信号按照频率不断进行IMF求解，直至不能再筛选出IMF为止，留下的信号称为残余信号。EMD的分解过程如下。

首先，求解t时刻的原始信号x（t）的全部极值，根据极大和极小值分别构建上包络线u（t）和下包络线l（t）。

然后计算u（t）和l（t）的算术平均值m（t），

m（t）=u（t）+l（t）2 。（1）

从x（t）中去除m（t）后，得到初次分解信号

h1（t）=x（t）-m（t） 。（2）

根据IMF的规则，判定信号h1（t）是否符合IMF条件，若h1（t）满足IMF条件，则h1（t）为x（t）的第1个IMF，记为c1。将待分解的x（t）替換为r（t）=x（t）-h1（t）。 若h1（t）不满足IMF条件，则将待分解的x（t）替换为h1（t）。

按照以上步骤不断地进行分解，直至没有符合IMF规则的项为止，剩下的残余信号满足以下规则时停止。

∑thi-1（t）-hi（t）2h2i-1（t）≤ε

，（3）

式中： ε为常量， 取值范围为［0.2，0.3］； hi（t）和hi-1（t）分别为第i次分解信号和第i-1次分解信号。

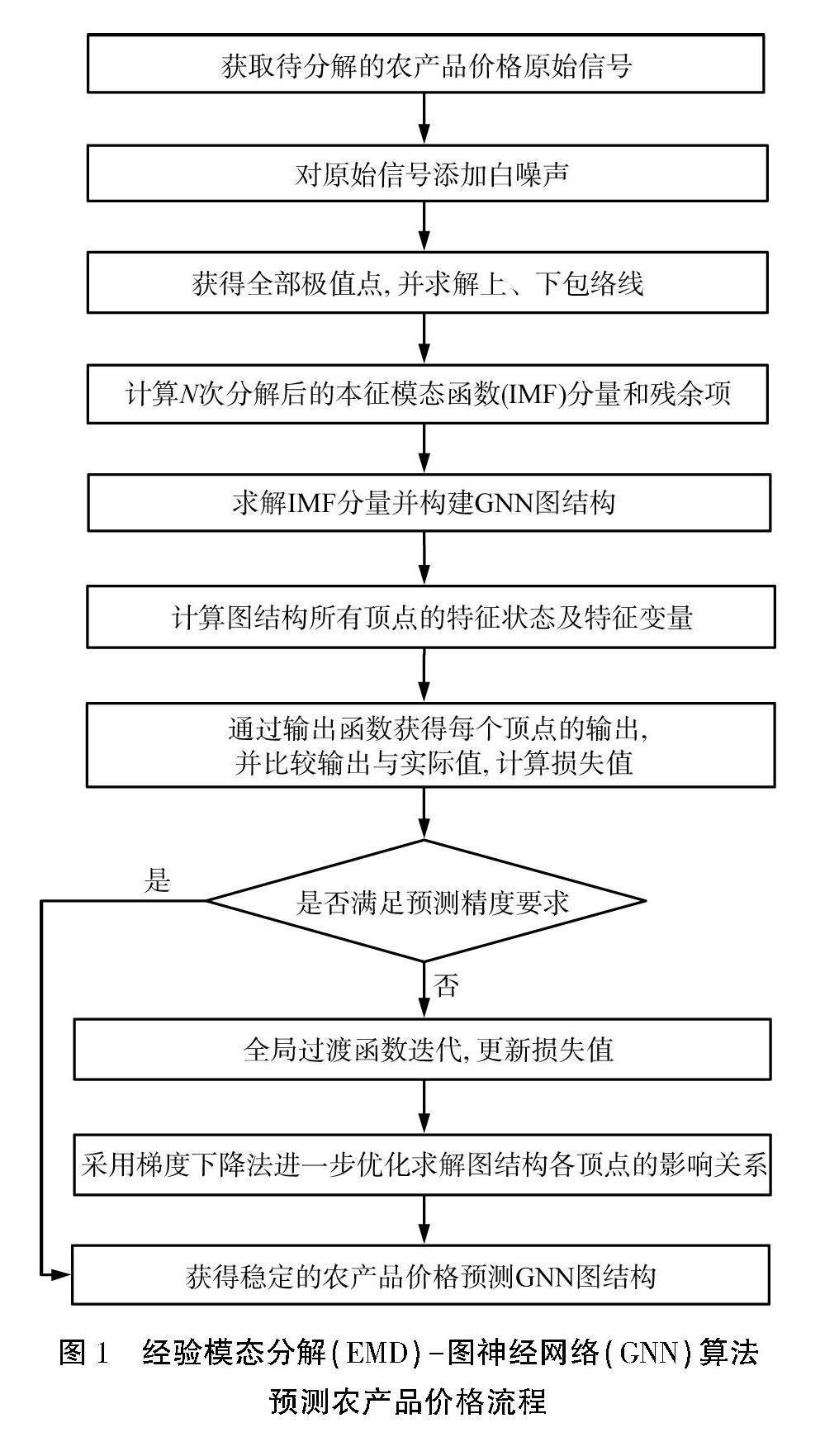
经过n次分解后，共得到n个IMF，这n个IMF用ci表示，0

x（t）=∑ni=1ci+rn 。（4）

在实际的EMD应用中，由于受信号提取精度的影响，而且在信号截取过程中易产生端点效应，待分解的原始信号容易受到噪声干扰，因此，为了解决因噪声而造成EMD分解结果不准的问题，本文中采用集成EMD进行信号分解。与传统EMD相比，集成EMD主要有如下改进：

1）待分解的信号由x（t）变为xm（t），计算方法［7］为

xm（t）=x（t）+ζ（t） ，（5）

式中： ζ（t）为噪声； m为加入噪声次数，最大值一般为100。

2）传统IMF项ci变为c－i，计算方法为

c－i=1M∑Mm=1cim ，（6）

式中cim为加入m次噪声后的ci； M为EMD噪声次数的最大值。

3）残余项r－也有变化，计算公式为

r－=1M∑Mm=1rm ，（7）

式中rm为加入m次噪声后的残余信号。

4）IMF项、 残余项和原信号x′（t）的关系［8］为

x′（t）=∑ni=1c－i+r－

。（8）

2  GNN

与传统的神经网络采用网格状数据进行建模不同，GNN可以采用图顶点展现更复杂的建模能力。圖G主要是由多个顶点v和边E构成的，G=（v， E），设图G中某个顶点v所包含的特征状态［9］为

hv=f（xv， xE， h′v， x′v） ，（9）

式中： hv为v的特征状态； xv为v的特征因子； xE为E的特征因子； h′v和x′v分别为v的相邻顶点的状态输入和特征因子； f为过渡函数。

根据hv和xv的取值，将两者传输至输出函数g，得到v的输出ov［10］，

ov=g（hv， xv） 。（10）

设H和X分别表示图顶点的特征状态堆叠及特征因子堆叠［11］，则经过全局过渡函数运算之后，即t+1轮迭代后，对每个顶点进行损失求解，得到总GNN的总损失L，计算方法［12］为

L=∑pv=1tv-ov 。（11）

式中： p为顶点总个数； tv为v的实际值。

3  EMD-GNN算法预测农产品价格

3.1  价格预测图结构的构建

农产品价格预测根据各农贸市场产品的供货量及需求量，结合影响农产品产量的其他因素等进行。

农产品价格主要由供求量决定；但是农产品的供求受到天气、 物流及市场环境等影响，要实现农产品的价格精准预测，必须充分考虑这些因素，因此在农产品价格预测的特征提取时，既需要提取各农贸市场顶点数据信号，又需要获取天气、物流等信号［13］，并将这些信号叠加共同构建原始信号，对该信号采用EMD进行分解，分解的IMF分量构建特征变量。

首先，使用EMD分解N个农贸交易市场的农产品特征变量；然后，利用得到的农产品特征变量构建一个图结构。在图结构上观测的农产品价格信号为X。假设历史农产品价格信号为X（t），则可通过预测函数，获得t+1时刻农产品价格。

假设农产品价格预测的信号提取时间片为EMD噪声次数的最大值M，从N个农贸市场的历史价格数据中获得的特征变量为V=（v1， v2， …， vM），并V将作为图结构的顶点，它们的价格之间是有一定的联系的，这种关系采用边E表示，两者关系的强弱用权重w衡量，这样便构建了一个图结构G=（V， E， w），根据M即可以得到M个数据。

3.2  农产品价格预测流程

EMD-GNN算法预测农产品价格流程见图1。 首先， 从各农贸市场获得农产品价格数据历史样本信号。 根据历史价格数据及天气、 物流等因素引入白噪声， 形成混合信号。 采用EMD进行分解， 获得的IMF分量和残余项。 然后， 求解IMF分量， 从而

构建特征样本。 根据时间片抽样的历史样本构建多个图结构顶点。最后， 采用GNN进行农产品价格预测。

4  实例仿真

为了验证EMD-GNN算法在农产品价格预测中的性能，进行实例仿真。选择某一线城市2015—2019年16个农贸市场中4种农产品的每日价格，具体数据集如表1所示，训练和测试样本个数之比为3∶1，通过前10 d数据对后1 d价格进行预测。首先对EMD-GNN算法的农产品预测准确率及均方根误差（RMSE）进行仿真；其次，测试EMD对GNN在农产品价格预测中的性能影响；最后，采用常用农产品价格预测算法与EMD-GNN算法相比较，对比不同算法的预测性能。

4.1  EMD-GNN算法的预测性能

采用EMD-GNN算法分别对4类农产品的样本信号进行价格预测训练，获得稳定的EMD-GNN预测结果， 分别选取各类农产品共100个样本进行预测， 结果见图2。从图中可以看出： 对于4类农产品测试样本， EMD-GNN算法获得的预测单价与实际单价非常接近， 未出现较大的预测偏移； 大米和苹果的价格偏移量最小， 猪肉价格偏移量最大。 为了量化4类农产品的预测价格偏移， 对预测结果的RMSE进行统计， 结果如表2。 从表中可以看出： EMD-GNN算法在4类农产品的价格预测的RMSE较小，最大值仅为0.236 1； EMD-GNN算法对大米的价格预测精度最高，RMSE均值仅为0.148 7，苹果和鸡蛋的价格预测精度也较高，但猪肉的价格预测精度最低，原因可能是猪肉的价格变动较频繁，在一定程度上干扰了EMD-GNN算法的价格预测。

4.2  EMD的优化性能

为了进一步验证EMD在GNN对农产品价格预测方面的优化性能，分别采用GNN和EMD-GNN算法进行4类农产品价格预测，所有测试样本的平均绝对误差（MAE）见表3。从表中可以看出，GNN、 EMD-

GNN算法对4类农产品价格预测的MAE差异较大，GNN算法的MAE基本维持在0.07左右，EMD-GNN算法的基本保持在0.02左右， 减小了71.4%， 结果表明， 经过EMD对原始农产品价格信号进行分解后， GNN算法具有更优的预测精度， 通过采用EMD对IMF分量进行有效提取，获得了更稳定的价格特征， 为GNN算法进行准确的价格预测提供了基础。

不同算法预测农产品价格的均方根误差（RMSE）见图3。 由图可以看出， GNN、 EMD-GNN算法对4种农产品价格预测的RMSE呈现较明显的分层现象。 对于同类农产品的价格预测， GNN算法的RMSE基本都大于0.25，而EMD-GNN算法的RMSE均小于0.25。对于不同类农产品，2种算法

GNN—图神经网络； EMD—经验模态分解。

图3  不同算法预测农产品价格的均方根误差（RMSE）

的RMSE表现也存在着较大差异： 对于预测精度最高的大米，EMD-GNN算法的RMSE比GNN的减小100%； 对于预测精度较低的猪肉，EMD-GNN算法的的RMSE也比GNN算法的减小95.65%。 总之， 经过了EMD对农产品历史信号进行分解处理后， 有效地提高了GNN算法对农产品价格的预测精度。

4.3  不同算法的预测性能

為了进一步验证EMD-GNN算法的农产品价格预测性能， 将近年来不同研究者在农产品价格预测中的常用预测算法，如反向传播

神经网络（BPNN）［14］、 引力搜索算法-相关向量机（GSA-RVM）［15］、 集合经验模态分解-长短期记忆（EEMD-LSTM）［16］进行预测精度对比，结果见表4和图4。

BPNN—反向传播神经网络；GSA-RVM—引力搜索

算法-相关向量机； EEMD-LSTM—集合经验模态分解-

长短期记忆； EMD-GNN—经验模态分解-图神经网络。

均方根误差（RMSE）和预测所用时间

从表4可以看出，4种算法在同类农产品的价格预测过程中存在较大差距，说明不同算法的价格预测精度差异较大，其中EMD-GNN算法和EEMD-LSTM算法的MAE最小，4类农产品价格的MAE均小于0.025，且EMD-GNN算法略优于EEMD-LSTM算法，GSA-RVM算法的MAE均大于0.05，说明经过EMD对农产品历史价格信号进行分解处理之后，更利于GNN算法实现农产品价格的精准预测。

从图4可以看出，4种算法的RMSE差异较大，从预测效率方面来看，BPNN算法和GSA-RVM算法用时较短，均在26 s完成预测，而EMD-GNN算法和EEMD-LSTM算法均需要28 s完成价格预测。由于EMD的信号分解需要消耗一定时间，因此导致这2种算法的价格预测时间稍有增加。

5  结语

本文中采用EMD进行农产品历史价格信号的有效特征提取，可以有效避免因噪声而引起的价格原始信号提取不准的问题，获得纯度更高的价格特征数据，从而为GNN算法进行农产品价格预测提供更优质的特征输入。通过GNN的图结构实现价格预测，对4类农产品价格均获得了较高的预测精度。后续研究将对EMD进一步改进，同时优化传统GNN算法，以提高EMD-GNN算法的农产品价格预测效率和稳定性。

参考文献：

［1］  赵汝鹏， 王昕， 李庆国， 等. 基于系统动力学模型的山东省农业供需水优化［J］. 济南大学学报（自然科学版）， 2022， 36（6）： 653.

［2］  刘合兵， 韩晶晶， 马新明， 等. 基于EMD-ELM模型的农产品价格预测研究［J］. 农业大数据学报， 2020， 2（3）： 68.

［3］  王新武， 靳佩芸. 基于集合经验模态分解和自回归神经网络的陇东农产品价格预测方法［J］. 兰州工业学院学报， 2022， 29（4）： 85.

［4］  李春华，李春静. GA优化GNNM（1，1）的煤矿涌水量预测［J］. 水电能源科学，2011，29（2）： 25.

［5］  SONY S， SADHU A. Multivariate empirical mode decomposition-based structural damage localization using limited sensors［J］. Journal of Vibration and Control， 2022， 28（15/16）： 2155.

［6］  余忠潇， 郝如江. 基于小波包分析与互补集合经验模态分解的轴承故障诊断应用［J］. 济南大学学报（自然科学版）， 2019， 33（6）： 547.

［7］  ADAM A M， KYEI K， MOYO S， et al. Similarities in Southern African Development Community （SADC） exchange rate markets structure： evidence from the ensemble empirical mode decomposition［J］. Journal of African Business， 2022， 23（2）： 522.

［8］  ZHANG H Y， LIU L， JIAO W， et al. Watershed runoff modeling through a multi-time scale approach by multivariate empirical mode decomposition （MEMD）［J］. Environmental Science and Pollution Research， 2022， 29（2）： 2822.

［9］  WU S W， SUN F， ZHANG W T， et al. Graph neural networks in recommender systems： a survey［J］. ACM Computing Surveys， 2022， 55（5）： 23.

［10］  ZHOU J， CUI G Q， HU S D， et al. Graph neural networks： a review of methods and applications［J］. AI Open， 2020， 1： 67.

［11］  WU Z H， PAN S R， CHEN F W， et al. A comprehensive survey on graph neural networks［J］. IEEE Transactions on Neural Networks and Learning Systems， 2020， 32（1）： 16.

［12］  ABADAL S， JAIN A， GUIRADO R， et al. Computing graph neural networks： a survey from algorithms to accelerators［J］. ACM Computing Surveys， 2021， 54（9）： 24.

［13］  沈虹， 李旭， 潘琪. 基于深度学习长短期记忆神经网络的有色金属期货市场预测研究［J］. 南京理工大学学报， 2021， 45（3）： 366.

［14］  商天文， 仉健维， 黄昊晨. 基于BPNN回归预测算法的专家数量预测模型［J］. 电信科学， 2023， 39（12）： 152.

［15］  ARUN M， MANIMEGALAI P. An efficient localization based on relevance vector machine with glow-worm swarm optimization for wireless sensor networks［J］. Journal of Engineering and Applied Sciences， 2018， 13（2）： 406.

［16］  吉长东， 杨超， 王强. 基于EEMD-LSTM模型的BDS卫星轨道预报精度分析［J］. 大地测量与地球动力学， 2023， 43（4）： 345.

（责任编辑：刘  飚）