基于多目标优化算法的输变电设备状态评估分析

山西昌和顺机电设备安装工程有限公司 侯建威

现阶段，部分电力企业主要依靠专家分析设备的运行数据，据此评估设备的运行状态，但此方法对专家的依赖性较强，若专家缺席将导致状态评估无法正常进行，同时评估结果可能由于专家主观因素的干扰而缺乏准确性。鉴于此，本文提出基于多目标算法的评估策略，以期依靠科学的方法准确评估输变电设备的运行状态。

1 状态评价分析

一个完全健康的在运设备的满分为100分，根据所选状态量的裂化程度，基本扣分值和权重系数进行扣分[1]。状态量劣化程度越高，基本扣分值越大，状态量权重系数越高，扣分越多，得分越少，相应的健康状况越差。根据现有的设备评价导则，我们依据设备的耗损程度将状态量的裂化程度分成Ⅰ、Ⅱ、Ⅲ、Ⅳ4个等级，权重值分为一、二、三、四4个等级。状态量的权重、劣化程度及对应扣分情况见表1。

表1 状态量的权重、劣化程度及对应扣分表

得出状态量的扣分值后，根据导则将该设备的健康状况分成四类：正常状态、注意状态、异常状态和严重状态。

2 基于多目标优化算法的输变电设备状态评估

2.1 目标函数

将最小化基分类器的数目和最大化决策分类器的泛化能力作为集成学习方法的主要优化目标，但两个目标相互矛盾，即决策分类器的精度会随着基分类器数目的减少而降低，难以同时兼顾两个优化目标[2]。基于此，本文采用多目标PSO 算法优化目标函数，在减少基分类器数目的同时提高分类精度。

目标函数1，分类精度：分类器的分类精度通过各样本的均方误差进行反映，其中均方误差最小则对应的是最大化分类精度。按照式（1）反映集成分类器的预测精度：

目标函数2，分类器数目：基本规律是基分类器的数量越少，则彼此间的多样性越丰富，可通过式（2）反映决策分类器Hs的数目：

基于前述分析，提出多目标优化函数：

2.2 D-S 组合规则

以贝叶斯推论扩展后的D-s 组合规则融合基分类器的输出，若目标分类器组合方式合理，可以集各信息源的结果于一体，获得良好的信息融合效果。

在D-s 组合下的组成函数中，以概率质量函数m最为重要，符合如下条件：

式中，X为融合目标结果。

置信度函数Bel和似真度函数Pl也是D-s 组合中的函数类型，分别作为概率质量函数的上限和下限，如下：

式中，A、B均为X的子集。

D-s 组合生成的最终决策结果由融合基分类器输出m和Im2得到，具体按照式（6）的方式进行融合：

2.3 评估模型

将富有多样性同时精度较高的基分类器作为研究对象，采用多目标优化算法构建决策分类器，具体如下。

收集数据集：包含各类指标数据，用于表征输变电设备的运行状态。

归一化处理：按照式（7），归一化处理输入数据，获得零均值和单位标准差。

式中，xnew为归一化的新样本；xstd为样本方差；xmean为样本均值。

划分数据集：随机排列输入数据，划分为两部分，第一，用于训练分类器的训练集。第二，用于测试分类器性能的测试集。

交叉验证：为评估基分类器的误差，采用10折交叉验证。

练分类器：从数据集中划分出训练集后，用于训练T个基分类器，确定各自的平均均方误差。

调用算法：随机初始化二值向量s，基分类器是否被选择则取决于s中的每一位，采用前述提及的分类精度和分类器数目两个目标函数使s的取值最优。

测试和验证非劣解：测试基于多目标优化算法确定的非劣解的性能，再用验证集评估。

选择最优解：从验证完成后的非劣解中挑选精度最高的部位，将其作为最优解。

D-s 组合：组合基分类产生的结果，此处完全遵循D-s 规则，以保证组合结果的有效性[3-4]。

测试：按照“选择最优解”确定最优解后，采用从数据集中划分出的测试集测试最优解。

2.4 仿真实验及结果分析

在不同的运行状态下，变压器产生的能量存在差异，发生的化学反应不尽相同，生成的气体主要有H2、CH4、C2H2、CH2CH4、CH2CH6，由于化学反应过程中产生的气体主要溶解在变压器油中，因此在评估变压器的故障类型时主要根据溶解气体的成分进行。根据变压器的运行状态，将其故障类型分为局部放电、电能放电和过热三大类，具体又可细分为六种故障，具体见表2。基于IEC 三比值法诊断变压器的故障，即比较等比值。

表2 变压器故障类型

2.4.1 数据集的获取

以多种等级和多种容量的变压器为实验对象，确定各自的溶解气体成分，按照变压器运行状态的不同，设定了90组训练样本和30组测试样本用于研究，数据集总量为120组。

2.4.2 基分类器及参数

基分类器的构建基于RBF 核SVM 进行，计算公式如下：

式中，σ为带宽，是影响特征空间样本分布规律的关键因素，与惩罚系数C共同影响SVM 的性能。考虑到SVM 为二分类器，在评估运行状态时采用RBFSVM 组合成多分类器，在此基础上做出相应的评估。

2.4.3 测试结果

训练样本的分类结果，如图1所示，总量为90组，诊断错误的数量为6组，具体情况是：1组将PD分为ED；1组将ED 分为OHF；1组将正常分为OHF；1组 将ED 分 为PD；2组 将OHF 分 为PD。测试样本的总量共计为30组，诊断错误的数量为2组，具体情况是：1组将ED 分为OHF；1组将正常分为OHF。根据两类样本的测试结果计算分类正确率，训练样本、测试样本均在93.3%，总体上具有较高的准确率，采用基于多目标优化算法评估变压器的运行状态是一种可行的方案。

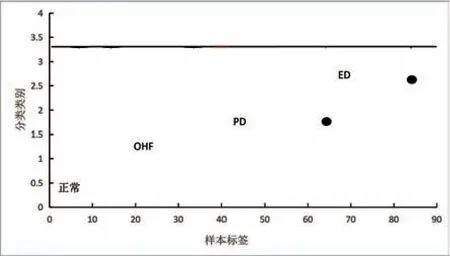
图1 训练样本诊断结果(黑色为实际类型；橘色为诊断类型)

2.4.4 比较试验

对比对象为IEC 三比值法、BPNN、单SVM三种方法，各方法采用的训练样本和测试样本相同，在此前提下将本文所提方法与前述三种方法进行对比，判断各方法在输变电设备故障评估中的准确性。BPNN 为反向传播神经网络，含有双隐层，通过反向传播算法优化网络参数。单SVM在20次试验后的参数结果为σ=0.05，C=20。按照不同的算法在样本条件相同的前提下进行诊断，各自的分类精度见表3；部分测试实例结果见表4。

表3 不同算法的诊断结果

表4 变压器故障诊断实例结果（其中错误诊断用粗体标出）

结合表3、表4数据做如下分析：IEC 三比值法，在状态评估中容易遗漏某些故障，评估结果的准确率偏低，如实例2和7所示，变压器故障类型的边界不明确，在边界比值附近时难以准确判断变压器的故障；相比之下，BPNN 的准确率有所提高，但在70%以内，仍未满足高精度的检测要求，只有在样本量足够大时才能够提高准确率；单SVM 的准确率高于IEC 三比值法和BPNN，在输变电设备状态评估中的应用效果相对较好；本文提出的基于MOPSO的方法是本次对比分析中准确率最高的方法，达到93.3%，能够进一步提高SVM 分类器的精度。

综上所述，输变电设备状态评估结果需准确，根据此要求，本文提出基于多目标优化算法的评估方法，训练得到基SVM 分类器，从中筛选出多样性良好且精度高的部分，基于此部分基SVM 分类器构建决策分类器，将变压器的运行状态分为正常、ED、PD、OHF 四类，根据变压器数据进行实例分析，将本文所提方法与其他常规方法对比，结果表明本文所提方法可有效提高SVM 分类器的精度，适用于输变电设备状态评估，可推广应用。