基于频谱图的土壤有机碳含量高光谱反演

熊志立高会议万莉

(1.安徽理工大学计算机与工程学院，安徽 淮南 232001；2.中国科学院合肥物质科学研究院，安徽 合肥 230031；3.安徽工业技术创新研究院六安院，安徽 六安 237100)

土壤有机碳(SOC)是土壤的重要组成部分，其主要由死亡植物和动物的遗体、有机废弃物以及微生物分解产生的有机物质组成[1]。SOC对于土壤的生物学、化学和物理性质具有重要影响，同时也在全球碳循环过程中扮演着关键的角色[2]。SOC含量变化是土壤生态系统的安全和全球可持续利用的重点[3]。传统的物理、化学方法检测SOC含量效率低，这些过程通常是破坏性的，会影响土壤原有的结构和组织，尤其是对于大面积的土壤调查来说，可能会导致土壤资源的浪费和破坏。高光谱技术大范围、高精度的数据采集能力，为决策者提供了全面的土壤信息，有助于土壤性质的快速、精准估算，为农业生产、土壤保护和环境监测提供了重要的技术手段[4-6]。

通过高光谱技术估算SOC含量，其中不同的数据的预处理对模型精度至关重要。众多学者对土壤光谱采用了不同的数据预处理方法[7-9]，如倒数(1/R)、取对数(lgR)、一阶微分(R′)等数学运算用来增强光谱数据与SOC之间的特征相关性，并构建了能够处理大量光谱数据的统计建模方法和机器学习模型[10，11]，如支持向量机(SVM)、偏最小二乘回归(PLSR)、卷积神经网络(CNN)等。聂哲等[12]以东北典型黑土区表层土壤为研究对象，对原始光谱开展一阶微分、倒数对数和连续统去除变换。钟亮等[13]以江西省奉新县北部土壤为研究对象，对光谱反射率进行微分变换，包括0.5阶微分(0.5DR)、1阶微分(1DR)、1.5阶微分(1.5DR)、对数的微分(LDR)等预处理方法。王海江等[14]以新疆盐渍化土壤为研究对象，对土壤样本光谱反射数据进行开根号、一阶微分根号处理、二阶微分根号处理、和连续统去除处理等多种预处理方法。综上，目前研究所使用的土壤特性高光谱反演方法大多局限于某一地区或者是某种土壤类型，以及目前的光谱数据预处理方法只是对频率域(光谱吸收率或反射率)进行变换，但没有直接考虑到波长域的影响。

本实验以LUCAS数据集为研究对象，运用分析短时傅里叶变换(STFT)和小波包变换(WPT)数据处理方法将光谱数据转换为可以充分体现土壤吸收率随波长变化的频谱图，而后利用构建的CNN模型，对其特征信息识别与提取，最后进行回归预测。本研究的目的，探索使用频谱图估测SOC含量对于大规模土壤高光谱数据集的可行性；构建基于频谱图的CNN回归模型用于SOC含量分析，并与偏最小二乘回归(PLSR)、一维卷积模型(1D-RDC)比较；对比STFT和WPT 2种变换的优劣，选出最优的估测模型。

1 实验材料与方法

1.1 LUCAS数据集

欧洲联盟统计局(EUROSTAT)发布的是LUCAS 2009表土数据库[15]。欧盟23个成员国20000个表层土(0～20cm)样品，数据参数包含粒度分布、pH值、有机碳(g·kg-1)、碳酸盐含量(g·kg-1)、磷含量(mg·kg-1)、总氮含量(g·kg-1)和光谱等特性，土壤类型包含农田、耕地、草地、林地等6种。光谱数据由漫反射光谱仪(XDS)记录光谱特征以0.5nm的光谱分辨率捕获400～2500nm范围，产生4200个数据点。

1.2 光谱数据选取与预处理

由于矿物土壤和有机土壤材料的光谱响应存在很大差异，数据集中绝大多数为矿物土，因此将数据集中的有机土样本剔除，保留约18000个矿物土壤样本。将约18000个样本划分为训练集和测试集，数据划分规则为随机划分。其中训练集样本占比80%，验证集样本用于检验模型准确度，占比为20%。样本中SOC含量最小值为0g·kg-1，最大值199.2g·kg-1，平均值29.35g·kg-1，中位数19.6g·kg-1。每个样本具有4200个数据点，对数据进行1∶4下采样(每2nm保留1个值)，下采样到1050个数据点。目的是减少数据的维度，去除数据集中的噪声和冗余信息，保留主要特征，减少存储和计算成本，提高数据处理和计算的效率，加快模型训练和预测的速度。

1.3 频谱图

谱图是信号在二维空间中的表示，其中信号的幅度由像素的值表示。STFT和WPT都是生成时频图的信号分析算法，土壤光谱数据没有时间域，所以本文中将波长域看作时间域，这种频谱图展示了土壤反射率随波长变化的情况，而非随时间变化的情况。

1.4 短时傅里叶变换

短时傅里叶变换(Short-Time Fourier Transform，STFT)是一种将信号分解成时频域的方法，用于分析信号的时变频谱特性[16]。具体来说，其将信号分成一系列长度相等的窗口，并对每个窗口内的信号进行傅里叶变换。每个窗口上的傅里叶变换产生1个时频图，所有窗口上的时频图按时间排列起来，形成1个二维矩阵，即时频矩阵。

给定1个输入信号x(τ)，STFT将其分解为若干个窗口函数的加权傅里叶变换。

式中，S(t，f)表示在时间t和频率ω处的频谱结果；w(τ-t)是窗口函数，窗口函数的长度决定了频谱的时间和频率分辨率；e-jωτ是复指数函数，表示频率为ω的正弦波。

STFT将输入信号x(t)在时域中通过窗口函数进行分段，并在每个窗口上执行傅里叶变换来得到频谱信息。窗口函数w(t)通常是一个具有良好频率特性的函数，如Hann窗、矩形窗等。通过对不同时间段的窗口信号进行傅里叶变换，STFT将时域的信号转化为在频域中随时间变化的时频图像。这样可以获得信号在不同频率上的时变特性，并提供信号的频谱时序信息。在本实验中，采用了土壤的光谱数据作为初始输入信号，并选用了Hann函数作为窗函数进行处理。窗口长度为64，窗口重叠数为32。Hann函数计算公式：

式中，n表示窗口内的样本索引；M表示窗口的长度。由LUCAS数据集中土壤光谱经过STFT得到的频谱图见图1a。

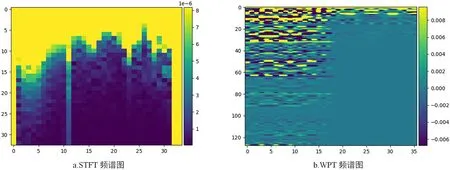
图1 频谱图

1.5 小波包变换

小波包变换(Wavelet Packet Transform，WPT)是小波变换的一种扩展形式，其将信号分解为不同频率和尺度的子频带，并且具有更高的灵活性和多分辨率特性[17]。WPT的关键优势在于其能够根据分析需求，灵活调整信号的频率和时间分辨率。与普通的小波变换相比，小波包变换在掌握和揭示信号的细微特征方面提供了更高的灵活性和更多的自由度。

设原始信号为x(t)，其中t表示时间。通过小波包变换，将原始信号进行分解与重构，小波包变换具体的公式如下。

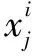
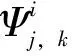
小波包变换的具体计算会涉及到选择合适的小波包基函数、尺度和频率参数的设定，以及数值计算的方法选择(如积分的数值近似等)。本实验选用的是Coiflet小波，以及7层变换层数，以LUCAS数据集中土壤光谱生成的频谱图见图1b。

1.6 模型构建方法

1.6.1 偏最小二乘回归

偏最小二乘回归(PLSR)是一种统计学方法。其通过计算输入变量与输出变量之间的协方差矩阵来确定输入变量的线性组合，这些线性组合被称为潜在变量。PLSR使用这些潜在变量来建立回归模型，从而在考虑输入变量相关性的同时，提高模型的预测性能和解释能力。

1.6.2 一维卷积神经网络

一维卷积(1D Convolution)是指对一维序列数据进行卷积操作，通常应用于时间序列数据或一维信号数据的处理，通过滑动窗口和对应位置元素相乘再相加的方式来提取特征[18]。由于1050个光谱数据较长，构建的残差扩张卷积神经网络(1D-RDC)的模块结构需多次使用扩张卷积和残差连接的方式，如表1所示，增强了输入序列中的特征表示能力，并且保持了输入序列的维度不变。通过使用扩张卷积可以捕捉更广泛的上下文信息，以增强特征提取的能力。整个一维卷积结构由3个模块加上2层全连接层组成。

表1 1D-RDC模块结构

1.6.3 二维卷积神经网络

卷积神经网络(Convolutional Neural Network，CNN)是一种深度学习模型，主要用于图像和视频等二维数据的处理和分析[19]。CNN的基本结构由卷积层、池化层和全连接层组成。卷积层是CNN的核心部分，其通过卷积操作对输入数据进行特征提取。通过多个卷积核，卷积操作能够提取图像中的局部特征，如边缘、纹理等，从而捕捉到图像的局部空间结构。通过不断堆叠多个卷积层，网络可以逐渐提取到更加抽象的特征。

CNN通过反向传播算法进行训练，不断调整网络的权重参数，使得网络能够学习到输入数据的特征表示，从而在分类、目标检测、图像分割等任务中取得优秀的性能。本次实验构建的卷积网络结构见表2，表2简要总结了这些层，其中包含4个卷积层2个全连接层。

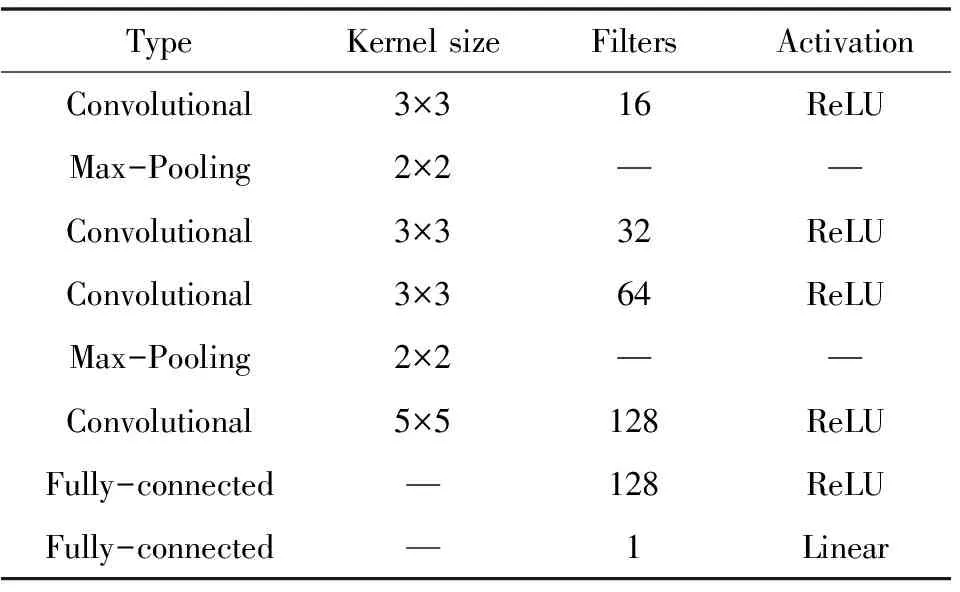
表2 二维卷积神经网络结构

1.7 精度评价指标

模型的模拟和预测性能通过决定系数R2和均方根误差RMSE进行验证，计算公式：

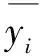
2 结果与讨论

2.1 实验结果和模型评价

本次实验共构建了4种估测模型：偏最小二乘回归(PLSR)，一维残差扩张卷积模型(1D-RDC)，短时傅里叶变换加卷积模型(STFT-CNN)，小波包变换加卷积模型(WPT-CNN)，4个模型预测值与实测值的关系如图2所示。由表3可知，训练集拟合的4个模型中，WPT-CNN表现最佳，获得了最高的决定系数0.90和最低的均方根误差9.13，具有更佳的精度和稳定性，相比于STFT-CNN的R2提高了10%，对应的RMSE降低了26%。其中PLSR模型和1D-RDC的R2相同，但在RMSE方面1D-RDC表现更好。模型在验证集上的回归适配性和预测准确度是评价其性能的关键指标，其直接体现了模型对于新数据的泛化能力。其中WPT-CNN的决定系数最高，为0.84，同时RMSE也是最小11.20，相比于STFT-CNN的R2提高了10%，RMSE降低了16%。在对比1D-RDC与PLSR模型时，观察到在采用相同光谱数据集和预处理方法的前提下，1D-RDC展现出了更佳的建模表现，其在关键性能指标上均超过了传统的PLSR模型。这一结果凸显了卷积神经网络模型在处理大量样本时的优越性，不仅具备高度的回归拟合能力，还能实现精确的预测，显示出其强大的学习力。在比较1D-RDC、STFT-CNN和WPT-CNN 3种方法时，研究发现，将数据转换为频谱图并输入到CNN模型进行预测分析，可以更充分地挖掘数据的潜力，实现深层次的训练，从而更准确地反映样本的实际测量值。

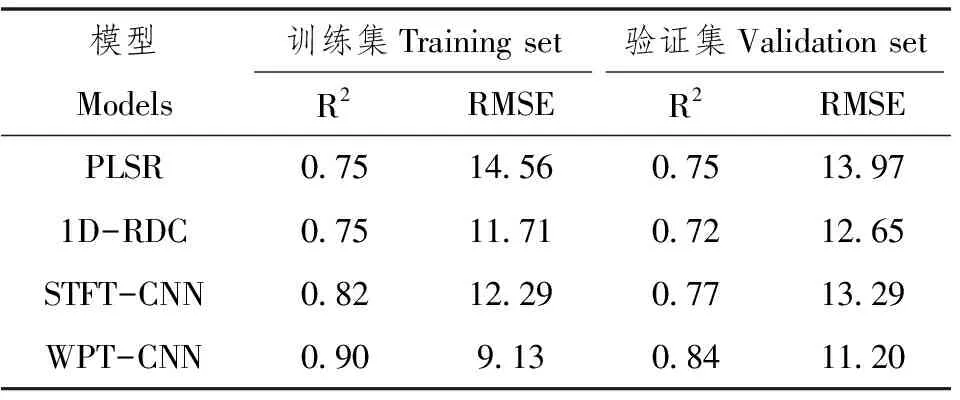
表3 不同模型的SOC估算精度对比

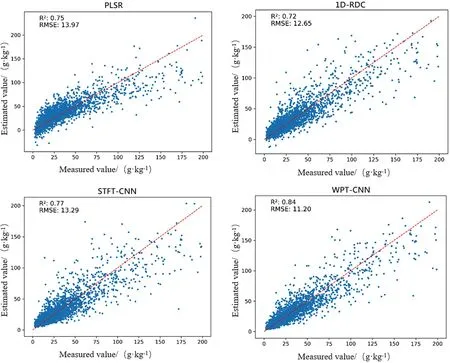
图2 不同模型SOC含量实测值与估测值比较

2.2 实验结果分析

本研究表明，CNN模型借助其深度学习架构，能够有效识别并学习频谱图的内在特性，从而获得更为精细的局部抽象特征表示。当这些深入挖掘的数据特征被用于SOC真实值的预测时，能够显著提升预测的性能。其中小波包变换的频谱图比短时傅里叶变换的频谱图具有更佳的回归效果。可能是因为小波包变换能够在时域和频域上提供更好的局部分辨率，可以显示信号的瞬时频率变化情况。相比之下，短时傅里叶变换在频谱分析上的时频分辨率较差，对于短时变化的频率信息的提取能力有限。另外，小波包变换对于噪声和干扰的抑制能力更强，能够更有效地提取出信号的有效信息，对于信号的频谱分析更具优势。

3 结论

本研究利用LUCAS土壤样本的高光谱数据，结合频谱图数据处理技术和CNN模型，成功实现了对土壤中有机碳含量的准确预测。结果表明，经过STFT和WPT数据处理后得到的频谱图能很好地被CNN模型学习并进行高精度拟合，可为大规模SOC含量高光谱估测提供一种新思路。其中WPT比STFT能更好地增强光谱信息特征。基于频谱图数据处理方法和卷积神经网络建模方法的SOC含量估测模型展现出了可行性和有效性。在大型土壤高光谱数据集的表现上，该模型不仅能够实现对训练样本的高精度拟合，还能够实现对检验样本的高精度估测。与传统模型相比，该模型的估测精度明显更优。然而，寻找最优网络参数以进一步提高估测精度等方面仍有待深入研究。