盖挖法基坑上跨既有地铁盾构隧道方案研究

吴 彬，付春青，彭 华，马文辉，杨纬华，刘 猛，刘 彤

（1.北京市轨道交通建设管理有限公司，北京；2.北京城建轨道交通建设工程有限公司，北京；3.北京交通大学，北京）

引言

随着城市的快速建设与发展，基坑邻近既有地铁隧道的工程数量越来越多，有的基坑甚至位于既有地铁隧道上方。基坑施工过程中的土方开挖、降水、加载等过程，都会使既有地铁产生一定的变形，而地铁列车的运营对隧道变形非常敏感。由此，对于该类基坑的设计、施工都提出了更高的要求。

针对新建基坑上跨既有地铁的工程，国内外学者开展了一定的研究。Marta[1]利用数值模拟手段，针对基坑开挖引起的近接隧道变形规律、受力特性以及加固和保护措施进行了多方面的研究。Sharma J S 等[2]通过数值模拟方法得到隧道的刚度、埋深、地质、下穿方式等因素与上跨工程施工引起的隧道变形大小存在直接联系。李志高等[3]分析了东方路下立交工程现场监测数据，得到了基坑开挖卸荷引起下方隧道纵向变形的总体规律和时空效应规律，推导了考虑时空效应影响的隧道隆起经验计算方法。黄宏伟等[4]通过PLAXIS 研究了外滩通道开挖对下卧延安东路隧道的影响，评价了不同隧道保护措施的效果。黄海滨等[5]采用有限元分析和现场实测方法研究了某箱型隧道基坑上跨已运营地铁隧道工程，优化设计了工程支护结构及基坑开挖方式。高强等[6]依托市政隧道上跨西安既有地铁2 号线盾构隧道为依托，根据拟定的设计方案，采用FLAC3D 有限差分程序对市政隧道基坑开挖对下卧地铁盾构隧道的影响进行数值分析，并对隧道抗浮进行验算。安伟博[7]采用MIDAS/GTS 建立了三维基坑模型，研究了杭州某基坑工程开挖对下卧盾构隧道变形的影响以及不同加固控制措施的效果。李宗阳等[8]采用现场实测方法研究了徐州粉土地区彭祖大道地道工程明挖基坑近距离上跨地铁盾构隧道的保护方案，提出了MJS 及管幕相结合的盾构保护措施。施有志等[9]采用有限元分析和现场实测方法研究了厦门地铁某停车场与地铁正线重叠段为依托，研究出入线明挖基坑施工对下卧隧道的影响以及采取变形控制措施的效果。

本文以北京某盖挖法深大基坑上跨既有地铁盾构隧道工程为依托，采用数值模拟分析基坑施工影响下既有隧道变形规律，比较讨论不同措施对既有隧道的保护效果，既保证基坑本身的稳定，又确保既有地铁安全运营，为相关工程提供理论依据和参考。

1 工程概况

新建基坑位于北京地铁某区间始发井结构正上方，如图1 所示。新建建筑结构形式为地上一层、地下三层的钢筋混凝土框架结构，基坑围护结构为113 根钻孔灌注桩，围护桩桩径1.0 m，桩长17.9 m～22.7 m。基坑底板埋深为14.6 m，与始发井结构顶板净距为5.915 m，与区间结构最小净距为9.194 m。

图1 工程周边环境

既有地铁双线盾构区间，区间线路为直线。盾构直径为6.0 m，结构顶部埋深约24.2 m，既有线间距14.0 m。

为确保开挖施工安全，减小对既有地铁盾构区间影响，从地面对区间上方土体进行加固。加固范围为基坑范围内、地铁盾构区间顶板以上6 m 土体。土体加固材料采用单液水泥浆或水泥-水玻璃双浆液,工程剖面如图2 所示。

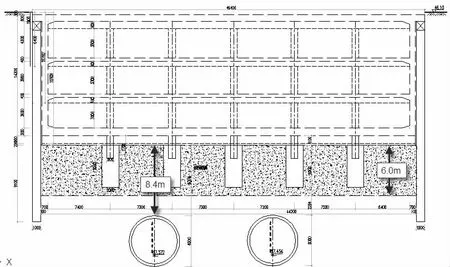
图2 工程剖面

基坑施工处岩土层从上到下依次为①房渣土、②1粉质粘土、②粉质粘土- 粉质粉土、③粉细砂、④1中粗砂、④卵石、⑤粘土、⑤1砂质粉土- 粘质粉土、⑤2粉细砂、⑥1中粗砂、⑥卵石。

2 模型的建立

结合实际工程，计算模型采用ANSYS 有限元软件建立地层- 结构三维实体模型，土体与基坑支护结构、新建地下室框架结构均采用实体单元Solid45 进行模拟，既有盾构隧道和竖井结构均采用壳单元Shell63 进行模拟。模型沿既有地铁线路方向（Z轴方向）取150 m，垂直既有地铁线路方向（X 轴方向）取120 m，沿地层深度方向（Y 轴方向）取50 m。地表为自由边界，土体四周及底部采用法向约束，如图3 所示。

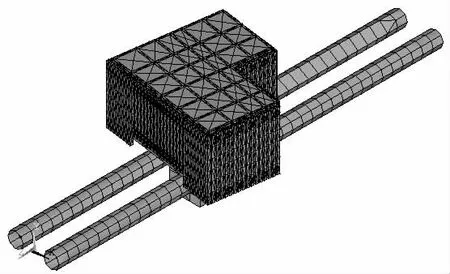
图3 新建基坑与既有隧道三维有限元模型

2.1 模型假定

（1） 土体为各向同性、均质的理想弹塑性体，对各层土体和地表作简化处理，使其在水平方向呈匀质层状分布。

（2） 在模型计算时，初始地应力只考虑土体自重应力；不考虑岩土体构造应力，使岩土体在自重作用下达到平衡状态，然后再进行基坑开挖施工。

（3） 根据工程地勘报告中所给出的土体参数来选取模型中需要的土层参数。

（4） 假定既有地铁结构变形和轨道结构变形一致。

（5） 假定在施工前轨道结构处于良好状态。

2.2 模型参数

根据地质勘查报告，依照地层特性对相近的土层参数取加权平均值。模型土层参数如表1 所示。

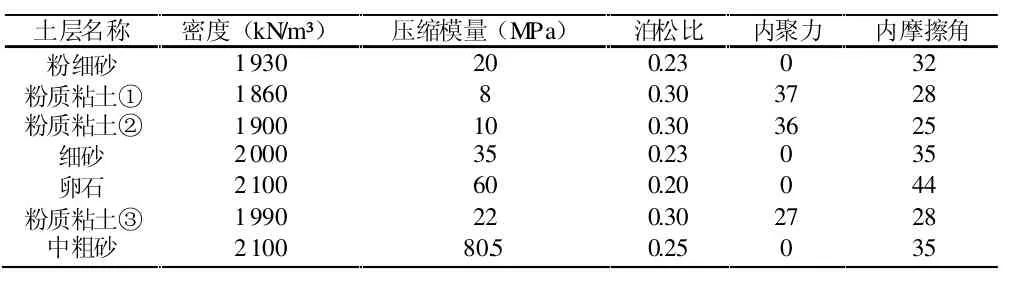
表1 土体参数

根据计算假定，既有及新建结构均视为线弹性材料，结构参数如表2 所示。

表2 结构参数

基坑施工采用盖挖逆作法，逐层分步进行，根据结构板的位置分为三大层，每层土方开挖在平面位置上又分南、北两幅依次进行，北幅待每层的南幅结构板、墙施工完成后再行施工，共分为11 个施工阶段。

3 模拟结果分析

3.1 计算结果分析

按工程方案进行数值模拟，经过计算，分析基坑开挖对地表沉降、隧道结构沉降的影响程度。基坑开挖结束后，既有地铁隧道变形由中间开挖位置处的峰值向两侧逐渐减小，曲线左右两侧对称。左线、右线最大上浮值为1.971 mm、2.371 mm，如图4 所示。

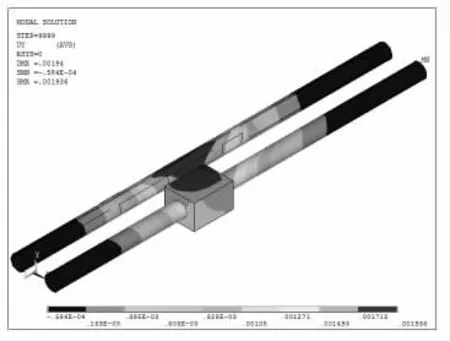
图4 施工结束时既有地铁隧道变形云图

3.2 方案对比分析

基坑的支护形式以及施工注浆情况的不同导致施工对既有地铁变形的影响程度不同，为了比较影响程度的差异，改变相关参数，如表3 所示，方案一、方案二对比分析注浆情况；方案一、方案三、方案四对比分析围护结构情况（桩径和桩距变化）。

表3 方案情况

3.2.1 注浆加固的影响效果

两方案下地表和地铁隧道的最大变形对比如表4所示，隧道竖向变形如图5 所示。

表4 方案一、方案二最大变形汇总（单位：mm）

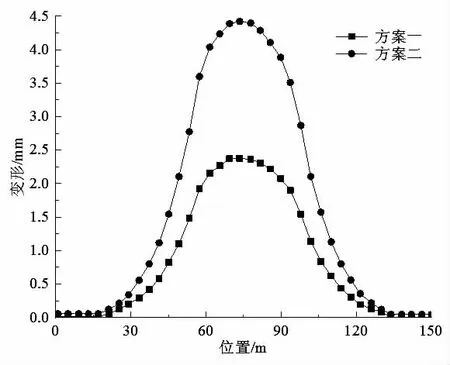
图5 方案一、方案二最大竖向变形量对比

在将方案由注浆6 m 改为不注浆后，隧道最大竖向变形由2.371 mm 变为4.42 mm，地表沉降最大值由5.34 mm 变为7.60 mm，超出安全控制范围，可见基坑开挖前对基坑下方处土体进行注浆加固是十分必要的，能够有效减小既有结构的变形。

3.2.2 围护桩结构参数的影响

三个方案下地表和地铁隧道的最大变形对比如表5 所示，隧道竖向变形如图6 所示。

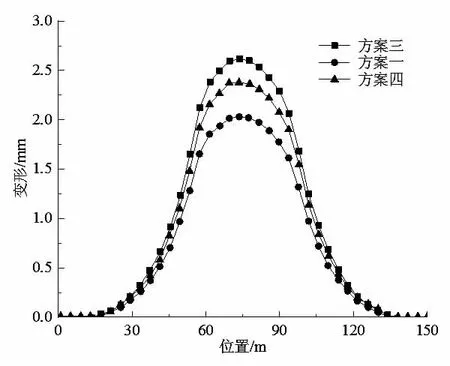
图6 方案一、方案三、方案四最大竖向变形量对比

（1） 方案一、方案三对比，在将围护桩直径由1.0 m 改为0.8 m 后，隧道最大竖向变形由2.37 mm 变为2.61 mm，地表沉降最大值由5.34 mm 变为5.47 mm，因此围护桩直径的改变能够影响既有结构沉降。围护桩直径越大，控制效果越好，既有结构沉降就越小。

（2） 方案一、方案四对比，在将围护桩桩距由1.5 m 改为1.2 m 后，隧道最大竖向变形由2.37 mm 变为2.03 mm，地表沉降最大值由5.33 mm 变为5.21 mm，因此围护桩桩距的改变能够影响既有结构沉降。围护桩桩距越小，即围护桩越密集，控制效果越好，既有结构沉降就越小。

（3） 在围护桩参数改变后，两方案中既有地铁的最大横向变形值由0.40 mm 变为0.44 mm 和0.34 mm，变化值仅有0.05 mm 左右，因此改变围护桩参数对结构横向变形影响效果不大。

（4） 从整体分析，围护桩参数改变后既有结构变形和地表沉降虽然有改变，但变化值并不大，与方案二注浆情况的改变对结构变形产生的影响相比，围护桩参数的改变对既有结构变形的影响较小。

4 结论

通过建立ANSYS 三维有限元模型，分析比较了不同施工参数下盖挖法基坑施工对既有地铁隧道的影响程度，得到如下结论：

（1） 基坑开挖前对基坑下方处土体进行注浆加固是十分必要的，能够显著减小既有地铁隧道的变形。

（2） 增大围护桩桩径，缩小围护桩桩距，可以减小既有地铁隧道的竖向变形，但与注浆加固相比，围护桩参数的改变对既有地铁隧道竖向变形的影响变化较小。

（3） 由于基坑开挖工程本身对下卧地铁隧道的横向变形影响程度较小，改变施工参数对横向变形的影响变化不大。