基于小波神经网络的模拟集成电路短路故障诊断方法

傅 巍，梁小利，夏 旭

（湖南安全技术职业学院（长沙煤矿安全技术培训中心），湖南长沙）

引言

模拟集成电路的故障主要分为短路故障和开路故障，其中短路故障对其性能的影响尤为严重。因此，对模拟集成电路的短路故障进行准确诊断有实际意义。针对模拟集成电路故障诊断的方法有多种。其中，直流故障字典方法是把线路的直流电压信号提取出来，并以此为基础构建一种新的故障字典。但一些复杂的电路，需要大量的试验数据。频域方法是将电路的频率响应作为故障的表征，具有理论上的成熟和对硬件的需求[1-2]。因此本文进行基于小波神经网络的模拟集成电路短路故障诊断方法的研究。

1 重构模拟集成电路原始信号

首先采集模拟集成电路短路故障原始信号，由于传感器以及外界环境的多变性，这使得采集到的数据存在着随机、非线性和复杂的调制分量[3]。为此，本文利用ITD 方法对原始信号进行分解，并将其分解为若干个具有不同峭度值的固有旋转分量，得到信息特征更大的重构信号，其设计内容如下。

1.1 原始信号的ITD 分解

对某原始数据集Xt=[x1,x2, …,xn]，采用ITD 算法进行一次分解，其分解结果如式（1）所示。

式中：L 为基线提取因子；Ht为固有旋转分量信号，Ht=（1-L）Xt；Lt为基线分量，Lt=LXt。

1.2 重构分量信号

将采集到的可听声信号经过ITD 算法分解后得到大量时域分量数据，由于峭度对前期机械故障的微小变化非常敏感，并且峭度值越大的分量信号包含越丰富的故障特征信息，可用其分析电力变压器故障前后可听声数据中冲击成分的含量，如下。

式中：K 表示峭度，用于信号处理和故障诊断领域的数值统计；Xrms为离散化均方根值；N 是样本数目；x（i）是已离散的后时间域成分信号[4]。在此基础上，以峭度标准为参考，选取具有高陡度的信号叠加，获得具有较强信息特性的重构信号。

2 提取短路故障信号特征

本文以小波分析为基础，对小波基函数进行改进以提取短路故障信号特征。Ψ（t）是一种小波生成函数，它是二次可积的，即Ψ（t）∈L2（R），其变换函数如下。

式中：ψ*(ω )为ψ(t)的傅里叶变换。ω 表示变换常量。针对单一的目标函数，本文拟采用二元小波分析方法，从电路信号中提取各频段的故障特征；采用Mallat算法对小波进行分解，实现在多个尺度下的逼近（低频）与细节（高频）两个分量，再对小波分解后的每一尺度下的高频分解系数进行绝对值相加，得到以比例次序排列的电路故障的特征矢量[5]。其详细步骤如下

（2） 计算各层次的各阶系数的绝对值之和。将第j 个层级的高频小波分解系数dj的绝对值的总和作为Dj，那么得到

式中：n 为序列dj中分量的个数。

3 定位故障点

假设模拟集成电路中的某个节点i 发生短路故障，则该节点的电阻值Ri 会发生变化[7]。用该电阻值变化，可以计算出该节点到电路中其他节点的电阻值变化量ΔRj(i)，其中j=1，2，...，n，n 为电路中除节点i外的节点总数。计算公式如下

其中，Rj为节点j 与电源或地之间的电阻值，Rj(i)为节点j 与故障点i 之间的电阻值。

在实际应用中，通过测量电路中的电压和电流，计算电阻值Rj和Rj(i)，并利用上述公式算出电阻值变化量ΔRj(i)。通过比较不同节点之间的电阻值变化量大小，确定短路故障点的位置。电阻值变化量最大的节点即为短路故障点[8]。

引入一个权重系数w(i，j)，表示节点i 和节点j 间连接权重。该权重系数可根据电路的结构和元件参数进行计算。将权重系数w(i，j)加入到ΔRj(i)的计算式中，得到加权电阻变化量ΔRwj(i)：

4 小波神经网络识别故障类型

利用小波神经网络构建识别故障类型。小波神经网络是以小波基函数值为隐层结点的传递函数，结构如图1 所示。

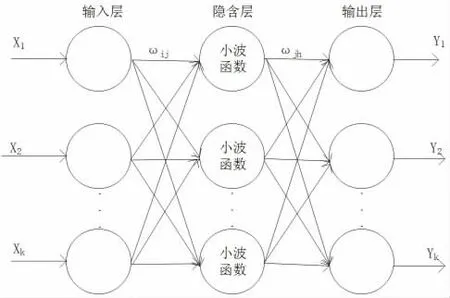
图1 小波神经网络拓扑结构

其中，参数X1，X2，Xk是小波神经网络的输入参数，Y1，Y2，Yk是小波神经网络的输出，而ωij，ωjh为小波神经网络输入层第i 个结点到隐含层第j 个结点的权重和隐含层第i 个结点对输出层第h 个结点的权重。

隐含层第j 的输出如式（7）所示。

其中，n（j）代表隐藏层第j 个结点的输出；yj代表了这个隐含层的传递函数；xi表示与该隐含层相连的输入层参数；bj为平移因子；aj为伸缩因子。

本文选择使用mexh 小波函数作为小波神经网络的传递函数。其数学表达式如式（8）所示。

通过上述分析，将传递函数设置为mexh 小波函数，隐含层节点个数先通过经验公式确认范围在4～13之间，隐含层节点的具体个数可通过对比实验进一步确认。

期望与输出结果如表1 所示。隐含层的节点数根据经验公式可知选取范围为：4～13。

表1 故障类型与输出结果的关系

综上所述，利用小波神经网络构建识别故障类型。

5 判别短路故障严重程度

研究模拟集成电路发生短路故障时特征波形的变化规律，提出合适的故障因子来描述故障的严重程度。特征波形如下。

（1） 故障点位置距首端距离越远，特征波形幅值越小。

（2） 特征波形幅值随故障点距首端距离增加呈指数衰减规律，且不同故障距离时的衰减程度不同。

（3） 同一故障位置下，特征波形幅值会随故障长度的增加而增大。

综上总结特征波形衰减特性近似为

式中：A 为特征波形的幅值；A0为在首端发生短路故障时的特征波形幅值，不受行波衰减影响；γ 为指数衰减因子，受脉冲波形频率、线路参数等多方面因素影响；d 为故障点距首端的距离。进而得到同一故障程度下的指数还原故障因子为A zhe(A0)＝A/e-γd。从测量得到的故障特征波形，可以得到特征波形的幅值A。然后，利用VMD-TEO 方法，得到了故障点到主末端的距离d。而指数衰变系数γ 可用下述方法求出。模拟集成电路短路时，并以其振幅为故障点到线路首端（2L，d）处的特征波形幅值。对于相同分支的匝间短路，而对于同相异根的模拟集成电路短路故障，其最大值用反时方法求出。

6 实验

6.1 实验准备

本文基于MATLAB/Simulink 仿真软件获取2600组不同的样本数据，输入是模拟集成电路负序电流幅值，输出则表示模拟集成电路短路故障的严重程度。故障类型输出设置见表2。

表2 故障类型输出编码

为验证本文诊断方法的效果，将本文基于小波神经网络的模拟集成电路短路故障诊断方法与直流故障字典方法和频域方法相比，选取训练样本40 个，测试样本20 个，展开实验。

6.2 实验结果与分析

样本数据选取负序电流幅值作为输入向量，故障的诊断结果是短路的严重程度。训练样本的部分数据如表3 所示。

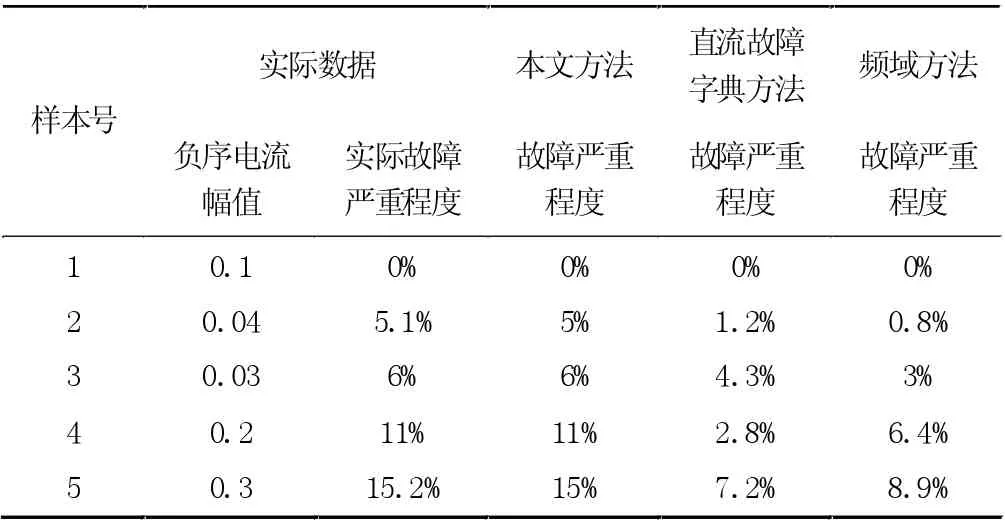
表3 短路故障诊断结果

从表3 得出，与直流故障字典方法和频域方法相比，本文基于小波神经网络的模拟集成电路短路故障诊断方法判别故障严重程度与目标值十分接近，表明本文本文基于小波神经网络的模拟集成电路短路故障诊断方法的效果好。

结束语

综上所述，本文基于小波神经网络的模拟集成电路故障诊断方法，提高故障特征的提取精度和神经网络的分类识别能力。同时，也将研究其他类型的故障，如开路故障等，以全面提升模拟集成电路的故障诊断能力。这些研究将有助于推动模拟集成电路故障诊断技术的发展，为电子设备的维护和检修提供更加可靠的支持。