织机车间直捻机筒纱抓取机械臂逆运动学求解方法研究

于俊康 江维 李红军 陈伟 陈振

摘 要：紡织车间中通过协作机械臂代替工人实现对直捻机筒纱的自动更换，可降低工人劳动强度，提高筒纱卷绕的生产效率。在对机器人进行运动学建模与分析时，逆运动学求解是机器人运动学中关键部分。传统法求机器人逆解存在求解速度慢、求解过程复杂、结果稳定性差等问题，采用传统BP（Back Propa- gationg Neural Network）神经网络求解又容易陷入局部极小值，针对上述问题，提出一种基于PSO优化算法（Particle Swarm Optimization Algorithm）的BP神经网络机械臂逆运动学求解方法，通过PSO算法对BP神经网络的权值和阈值进行多次迭代优化，避免了局部最小值的问题，提高了神经网络的全局搜索能力。采用 D-H法建立机器人运动学模型，根据机器人正运动学方程由关节角度解得末端位姿，将解得结果作为数据集，通过学习算法经多次迭代确定神经网络的模型参数，并对神经网络进行性能检验。实验结果表明： PSO-BP神经网络相比于传统的BP神经网络收敛速度快，该模型在搬运机器人逆运动学求解中精度高，满足纺织车间直捻机筒纱抓取作业的需要。

关键词：纺织车间；直捻机；筒纱卷绕；机械臂逆运动学；PSO-BP神经网络

中图分类号：TP242   文献标志码：A  文章编号：2097-2911-（2024）01-0021-12

Study on the Inverse Kinematic Solving Method of Grasping Mechanical Arm in Loom Workshops

YU Junkang a， JIANG Weia， b*， LI Hongjuna， CHEN Weia ， CHEN Zhena， b

（Wuhan Textile University a. School of Mechanical Engineering and Automation;

b. Hubei Provincial Key Laboratory of Digital Textile Equipment， Wuhan 430200， China）

Abstract：In the textile workshop， the automatic replacement of cylindrical yarn packages on the twisting ma- chine is achieved by using a collaborative robotic arm instead of human workers. It can reduce the labor intensi- ty of workers and improve the production efficiency of winding yarn packages. In the process of modeling and analyzing the robot's motion， the solution to inverse kinematics is a critical aspect of robot kinematics. Tradition- al methods for solving the inverse kinematics of robots suffer from issues such as slow computation speed， com- plex solving processes， and poor stability of results. Utilizing the traditional Back Propagation Neural Network （BPNN） for solving also tends to get stuck in local minima. To address these challenges， this paper proposes a method for solving the inverse kinematics of a robotic arm based on the Particle Swarm Optimization Algorithm （PSO） optimized Backpropagation （BP） neural network. Through multiple iterations using the PSO algorithm， the weights and thresholds of the BP neural network are optimized， preventing it from getting stuck in local min- ima and enhancing its global search capabilities. The robot's kinematic model is established using the Denavit- Hartenberg （D-H） method， and the end-effector pose is obtained by solving joint angles through the robot's for- ward kinematic equations. The results obtained serve as a dataset， and the model parameters of the neural net- work are determined through multiple iterations using a learning algorithm， followed by performance testing. Experimental results indicate that the PSO-BP neural network converges faster compared to the traditional BP neural network. The model exhibits high precision in solving the inverse kinematics of the material handling ro- bot， meeting the requirements for yarn-grabbing operations in the textile workshop.

Keywords： loom workshop；twisting machine；winding yarn packages；inverse kinematics of the robot arm； PSO-BP neural network

中国是纺织生产大国，纺织技术在国民经济、生产、生活中占据重要地位。直捻机是一种重要的纺织装备，其功能是将两根原丝加捻后合并一起形成纱线，再对纱线进行卷绕操作形成筒纱，最后取下直捻机上卷绕好的筒纱进行染色。传统的筒纱取放依靠人工，对于大型纺织车间，该方式效率低、劳动强度大，亟需开发一款能够辅助甚至替换人工进行筒纱抓取作业的智能化装备，因此，研究开发织机车间直捻机筒纱抓取智能装备具有重要理论意义与实际应用价值[1-2]。利用 AGV搭载机械臂辅助甚至替换人工实现织机车间直捻机筒纱自动抓取是一种行之有效的手段[3-4]， AGV到达作业点后，机械臂抓取筒纱过程中需要通过各关节协调运动，在固定的坐标系中，抓取筒纱其实质是由目标抓取点反推机械臂各关节运动参数的过程即机械臂的逆运动学问题[5]。机器人正运动学求得的位置和姿态是唯一确定的，而逆运动学求得的各关节角度通常有多个解或有不存在解的可能，甚至会出现奇异解[6]，因此在抓取机械臂众多逆解中寻求一组最优解以保证机械臂实现高性能抓取就显得至关重要。

对机器人各关节求逆解是机器人运动学中重要的一步[7]，传统的机器人逆运动学求解有代数法、几何法和数值解法。几何法是根据机械臂各杆件的平面几何关系和三角学原理求解各关节角度[8]。如卢喆等[9]中针对六自由度机器人求解复杂、几何定义模糊等問题[10]，对前3个轴线不相交的关节采用几何法求解，后3个轴线交于一点的关节采用Paden-Kahan子问题的插值法进行求解，但对高维、非线性的方程组求解时，存在计算效率低、难度大的问题。数值解法是通过数值逼近、差值或有限元计算来求得一组满足运动学方程的近似解。如林贞国[11]通过对偶矩阵的方法来求逆解，但该方法求解的难度较大，计算时间长，无法得到所有解，不适于实时性要求高的场合。代数法在运算速度和精度上有了较大的提升，但推导过程复杂，且机器人必须满足Piper 准则[12]（即六关节机器人中有三个连续关节的轴线交于一点或相互平行）才能使用该方法。人工智能的发展为机器人逆运动学求解提供了新的思路[13]。最常见的是利用BP神经网络[14]和RBF 神经网络[15]求逆解，如陈平等[16]采用权值优化后的 RBF 神经网络，来对机器人运动学求逆解。杨萍等[17]通过含有两个隐含层的BP神经网络对机器人求逆解。但当处理的数据较多时就会降低网络的运算速度。有专家提出基于智能优化算法提高神经网络的运算性能。如石建平[18]提出一种基于改进的克隆选择算法来对机械臂运动学求逆解，该方法下种群多样性的保持能力强，能够处理常规法无法解决的冗余机械臂逆运动学求解问题。董云等[19]将传统的解析法与遗传算法相结合，提高了全局寻优能力使机械臂在运动过程中保持良好的稳定性和避障性能。陈睿等[20]采用竞争的多变异策略差分进化算法分别对局部和全局种群进行参数标定，提高了三自由度并联机器人的运动精度。

综上所述，本文提出一种PSO优化BP神经网络的机器人逆运动学求解方法。PSO算法是基于群体智能的优化算法[21-22]，通过群体粒子间的合作与竞争搜寻最优解，该算法计算速度快、全局搜索能力强。通过PSO算法优化BP神经网络权值和阈值，改善网络结构，解决了BP神经网络易陷入局部极小值的问题，提高了网络的泛化性能和训练速度。将优化后的PSO-BP神经网络算法应用到纺织车间筒纱装卸六自由度机械臂上，实验结果表明，PSO-BP 神经网络比传统的 BP神经网络得到的运算结果精度更高，改进后的神经网络输出结果的均方根误差为0.071，且误差波动小，为大型织机车间多自由度机械臂逆运动学求解及作业控制提供了新的思路。

1 纺织车间协作机器人运动学建模与分析

1.1 机器人结构与作业流程

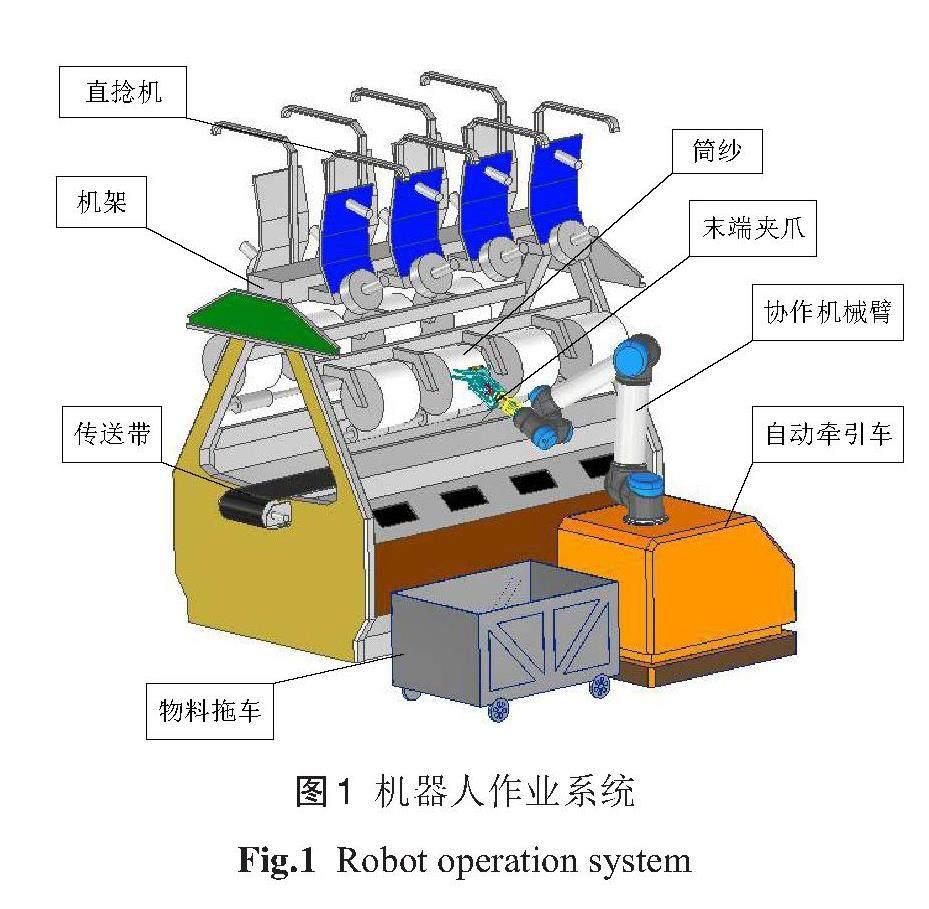
全自动纱筒更换的智能纺织系统包括直捻机、协作机械臂、末端夹爪、自动牵引车（AGV）和物料箱如图1所示，协作机械臂安装于AGV上，该机械臂系统是一个6-DOF机构，各关节依次为旋转关节、俯仰关节、俯仰关节、旋转关节、旋转关节、旋转关节，末端执行器，用来抓取纱筒，以完成对直捻机或倍捻机上纱筒的更换。牵引车后搭载的物料车用来存放筒纱和空纱管。

当直捻机某一工位的纱筒卷满纱线时，控制终端就会向机器人发送作业指令，AGV 接收到指令后通过地磁导引线牵引物料车移动到待作业位置，此时的机械臂处于初始状态。机器人到达作业位置，通过机械臂各关节的配合完成末端与筒纱的初始定位，末端夹爪取下筒纱，并放置在物料箱内，再通过各关节的配合将空纱管安放在工位上，此时已完成对一个工位上纱管的更换。AGV 继续移动到下一个待作业工位，重复上述操作，直到完成整个车间作业为止，其完整的操作流程如图2所示。

1.2 机械臂连杆坐标系建立

建立筒纱抓取机械臂各关节坐标系，如图3所示，获得各连杆之间的相对运动和位姿关系。通过改进D-H法描述机械臂各连杆坐标系之间的关系，其中各关节均绕Z轴旋转，α为坐标系绕X轴旋转的角度，a 为连杆长度，d 为连杆关节偏移量，θ为坐标系绕Z轴旋转角度。

最终，得到协作机械臂 D-H 参数表，如表1所示。

1.3 机械臂正运动学推导

将表1中机械臂 D-H 参数带入相邻杆件坐标系的位姿变换矩阵，得到相邻连杆之间的变换矩阵 i（i）?1T（i =1，2，3，4，5，6），如公式（1）所示。

公式（1）中：Cθ表示 cos θ ， Sθ表示 sin θ。根据机器人正运动学，将公式（1）相邻杆件齐次变换矩阵依次左乘可得到机器人基坐标与机器人末端的位姿变换，即机械臂的齐次变换矩阵如公式（2）。

公式（2）为机器人运动学正解，其中 R =[nx，ox，ax ; ny ，oy ，ay ; nz ，oz ，az]表示机器人末端执行器的姿态，P =[px，py ，pz]为机器人末端的坐标位置，并以机器人末端的位置和姿态参数作为机械臂操作空间的数据集。按 z?y?z 轴的旋转顺序对姿态 R 进行欧拉变换得到偏转角γ、俯仰角β、回转角α ， 如公式（3）所示，与 px、py、pz 组成包含6个变量的数据集，作为 BP 神经网络的输入量，经神经网络模型的运算得到机械臂各关节的角度θi （i =1， 2， 3， 4， 5， 6）。

α= ATAN2（ay ， ax）

β= ATAN2（ax cos α+ ay sin α， az）  （3）

γ= ATAN2（-nx sin α+ ny cos α， oy cos α-ox sin α）

公式（3）中ATAN2表示反正切函数，完整形式为：ATAN2（sin，cos），括号内依次为角度的正弦值和余弦值。

2 织机车间机械臂BP神经网络逆解求解方法

2.1 BP神经网络基本原理

BP神经网络是一种根据误差信号反向传播和BP算法训练的多层前馈型神经网络，具有良好的非线性拟合能力，可应用于多输入多输出的非线性系统。该网络结构由三层区域组成，各区域均含有多个神经元，每个神经元可将外部输入或上一神经元的输出作为该神经元的输入信号，不同的输入信号经过加权处理后进行累加，通过激活函数得到输出信号[23]。单个神经元如图4所示，X1至Xn 为该神经元的输入分量，Wi1至 Win 为各输入的权重，ui 为该神经元的组合输入，即：ui =∑j（n）=1xj wij ，组合输入ui 与阈值bi 计算后得到输出 vi ，即：vi = ui + bi ，将 vi 通过激活函数f（·）进行处理可得到最终的神经元输出 Yi。

BP 神经网络反向传播分为：工作信号的正向传递和误差信号的反向传递。其中误差的反向传递是 BP 神经网络的核心[24]，主要原理是采用梯度下降法即沿着实际输出与期望结果之差的平方和减小最快的方向，经多次迭代对网络的权值和阈值进行优化，直至实际值与理想值的误差最小或达到最大迭代次数时，训练结束后，输出模型参数，得到最终的神经网络模型。

2.2 BP 网络结构的设计

良好的神经网络结构保证了运算结果的准确性。针对本文中六自由度机械臂，根据BP神经网络的基本结构特点，设计了6输入、6输出的三层神经网络结构如图5所示，三层区域分别为输入层、隐藏层、输出层，6个输入节点分别对应机械臂末端姿态参数γ、β、α和位置参数 px、py、pz ，输出层的6个输出节点分别对应机械臂6个关节变量即θ1、θ2、θ3、θ4、θ5、θ6。

根据公式（4）确定合适的隐藏层节个数的取值范围，其中，h表示隐含层节点数，m表示输入层节点数，l表示输出层节点数，α取1～10之间的常数。通过公式可选取3～13个隐藏层节点，根据黄金分割原理不断缩小取值区间，直到神经网络的输出更加逼近真实值时，最终选取11个节点单个隐藏层的神经网络。

2.3 基于PSO算法的BP神经网络设计及改进

BP算法的实质是以梯度下降法求误差函数的最小值，即通过修正权值和阈值使输出结果的误差在期望误差范围内。考虑到初始权值和阈值的选取对BP神經网络性能影响较大和易陷入局部极小值的问题，影响神经网络的性能和准确性[25]，可通过启发式算法和基于数值最优化理论的训练算法来对BP神经网络进行优化。神经网络的输入向量为 xm （m=1～6），输出向量为 yn （n=1～6），隐藏层输入向量为 Hi 、输出向量 Ho 。机械臂末端位姿参数输入到输入层，待输入到隐藏层的数据经过加权处理，如公式（5），将隐藏层输入向量代入 sigmoid 激活函数解得隐藏层输出向量，如公式（6）。同样的方法得到输出层输入向量yi 和输出层输出向量yo，如公式（7），（8）。

上述公式中 H k）表示第k代样本数据输入到第j个隐藏层节点所得到的隐藏层输入向量，H ）为对应的隐藏层输出向量，其中j=1～11，ωmj 为输入层 m 节点与隐藏层j 节点间的连接权值，bj 表示隐藏层j节点的阈值，xm 为输入层m节点的输入向量。 y n（k））表示 H ）输入到输出层n节点所得到输出层输入向量，y 为输出层n节点的输出向量，其中 n=1～6，ωjn 为隐藏层j 节点与输出层n节点之间连接的权值，bn 表示输出层n节点的阈值。将输出层的实际值与理想值做差，得到均方差损失函数Loss，如公式（9）。

公式中 d ）为第k次迭代在输出层n节点的理想输出值。误差函数 Loss 分别对误差函数 Loss的隐藏层与输出层间的权值和输入层与隐藏层间的权值求偏导得到公式（10）。

定义δ ）为（d k）- y ））?f'（y nk ）），δ k）为 k）?ωjn ?f'（H k）），d ）表示输出层n节点的理想输出值，学习率μ取0.5。通过调节δ k）、δ k）来修正各层之间连接的权值ωjn 、ωmj 和阈值 bn 、 bj ，使实际输出更接近理想值，如公式（11）。

计算参数修正后神经网络的实际输出值，代入公式（9）得到神经网络的输出误差，当所有误差值在理想范围内，运算结束，得到最终的神经网络模型，否则继续沿着误差平方和减小的方向修正权值和阈值直到输出的误差在理想范围内。

采用粒子群优化算法（PSO）对BP神经网络进行对神经网络的权值和阈值进行初始化操作，以提高BP神经网络的全局寻优能力。系统中的随机粒子在搜索空间中经适应度函数计算和多次迭代来寻找最优解。假设在D维空间内，设置种群规模N=50，最大迭代次数T=220。空间中的粒子根据局部最优解和全局最优解来更新自己的速度和位置，如公式（12）。

公式中：v k）（t）和 x k）（t）分别表示 t 时刻粒子j在k维上的速度和位置。ω为惯性权重，值越大表示粒子种群收敛速度越快，全局寻优能力越强，一般在0～1之间内取值。 pb 为粒子本身的历史最优解，gb 为整个种群中粒子的历史最优解。根据标准PSO算法的参数设置要求，保证全局搜索和局部搜索的能力相等，现令加速度常数 c1= c2=2。 rand（0， 1）表示0～1的随机数。将实际输出均方根误差定义为适应度函数，如公式（13）。

2.4 织机车间抓取机械臂神经网络逆解求解

基于筒纱抓取六自由度机械臂的结构特点，设计了六输入、六输出的PSO-BP三层结构的神经网络模型。输入变量X=[γ，β， α，px，py ，pz ]包含机械臂末端的位置和姿态，输出向量 Y=[θ1，θ2 ，θ3， θ4 ， θ5， θ6]为机械臂各关节的角度值。对神经网络进行离线训练和在线运行，以提高神经网络模型的泛化能力和性能。离线训练是将网络的输入值和对应的输出值作为数据集，输入到PSO-BP 神经网络中，经PSO算法对网络权值、阈值的优化和BP算法对误差的反向传播以缩小实际输出与理想值之间的偏差。在线运行阶段，将机械臂末端的位姿参数输入到神经网络模型得到实时的机械臂逆解即各关节角度大小。

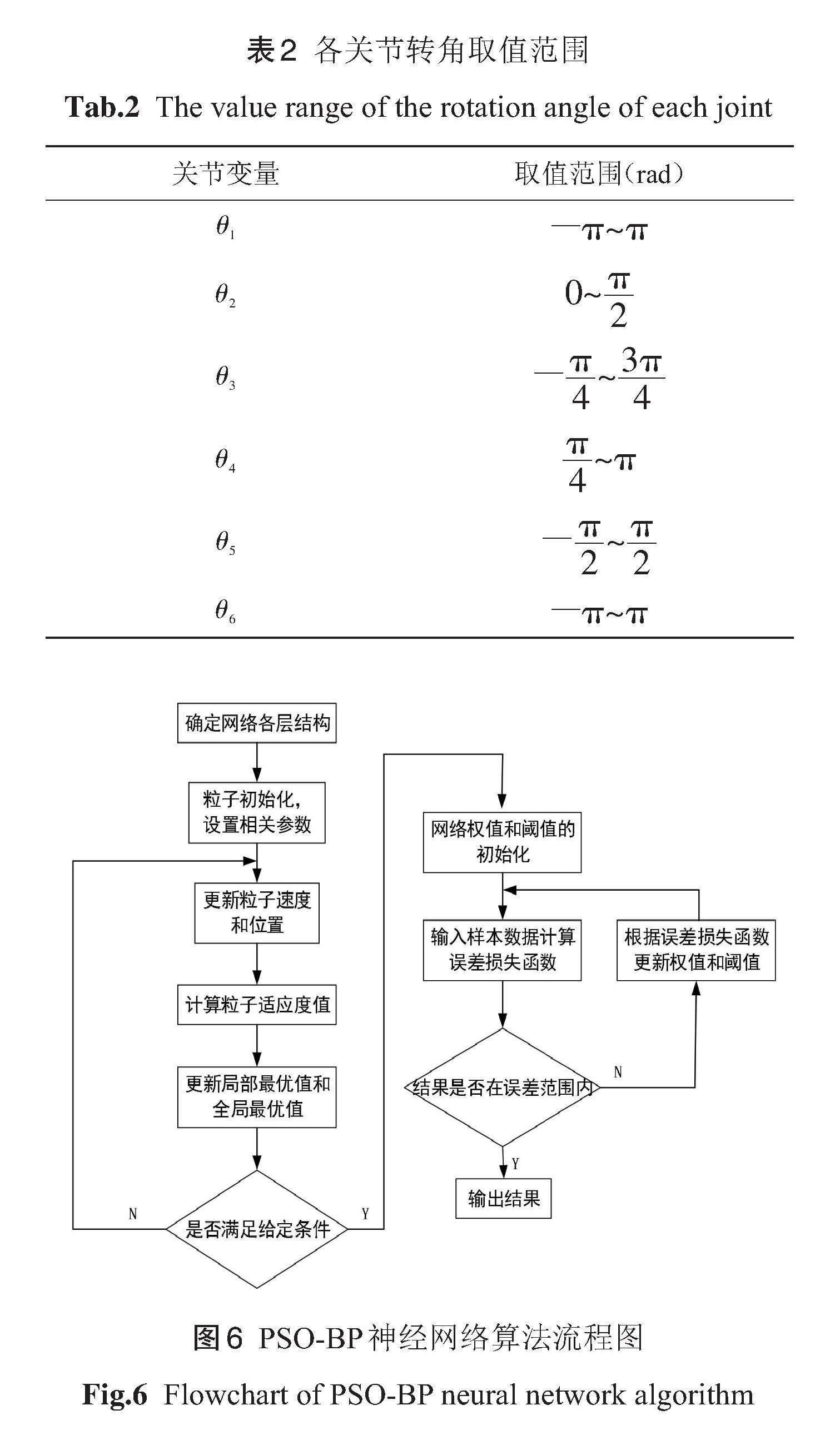
根据实际作业要求确定各关节转角范围，如表（2），通过 MATLAB Robotic 工具箱完成对机器人正运动学求解。在关節变量的取值范围内随机抽取1100组关节角度值，经公式（2）求解机器人正运动学，通过公式（3）解得机械臂末端的姿态角，得到机械臂的输入数据集，在MATLAB 环境下对神经网络模型进行训练，确定关键参数。图6为PSO-BP神经网络训练流程图。

3 仿真与实验分析

3.1 仿真实验

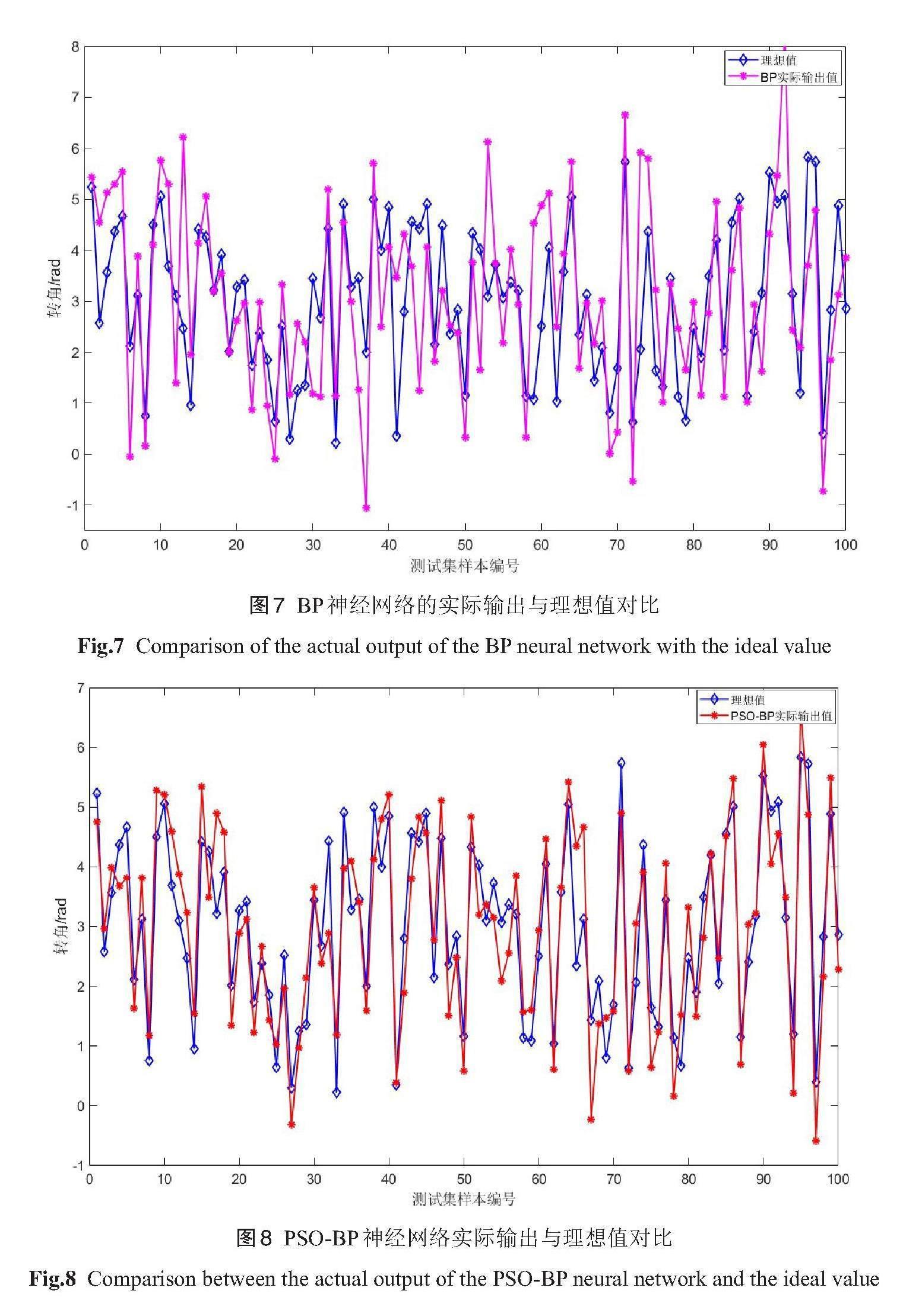
在 MATLAB 环境下根据机器人正运动学解得机械臂末端的位姿参数（γ、β、α、px、py、pz ），与各关节角度组成含有12个参数的1100组数据的数据集（γ、β、α、px、py、pz 、θ1、θ2、θ3、θ4、θ5、θ6），其中前6个参数为神经网络的输入量，后6个参数为输出量。将所有数据记录到表格中，表中每一列对应不同的参数，随机抽取1000组为训练集，余下的100组为测试集。测试集的位姿参数分别经过粒子群优化前后的BP神经网络运算，分别得到对应的实际输出值，绘制实际输出与理想输出的折线图，如图7，图8。观察图像，相比于图7，图8中神经网络的实际输出与理想值的拟合程度较高。整体上看，PSO- BP神经网络输出值更加接近理想值，相比于传统的BP神经网络，经过粒子群优化的BP神经网络具有更准确的预测能力。

提取神经网络对关节1的预测情况，如表3所示，分析PSO算法对BP神经网络预测性能的影响。其中BP神经网络对关节1的最大输出误差为0.386，均方根误差为0.139，PSO-BP神经网络对关节1的最大输出误差为0.199，均方根误差为0.071。经粒子群优化的 BP 神经网络最大输出误差和均方根误差都小于传统BP神经网络的输出误差。分析图9测试集中的100个样本误差，可知PSO-BP的输出的误差波动幅度较小，且均在误差范围内。

分析BP神经网络在粒子群算法优化前后的收敛性能，在相同的实验条件及相关参数下进行对比，得到BP神经网络和PSO-BP神经网络迭代收敛变化趋势，如图10。传统的BP神经网络经16次迭代后适应度函数达到最小值为1.015，而PSO-BP神经网络训练迭代到第8次后的适应度值达到最小值为0.920。通过图10，传统的BP神经网络收敛速度较慢，全局的寻优能力较弱，而经过粒子群优化的BP神经网络在计算精度和收敛速度上都有了一定的提高，满足筒纱抓取中对机械臂的逆运动学求解和对机械臂的实时定位控制。

4 结论

（1）提出了一种纺织车间加捻机筒纱自动抓取的智能化解决方案，通过AGV上搭载了六自由度机械臂，其末端能够到达作业空间的任意位置，末端夹爪可对筒纱进行抓取，能够实现对直捻机上纱管的更换任务。

（2）通过分析六自由度机械臂的结构和机械臂末端的位移参数，利用粒子群优化算法，提出了一种6输入6输出的PSO-BP神经网络来对直捻机筒纱抓取机械臂求逆解。该方法能够处理高维问题和各关节间的强耦合关系，并且 PSO- BP 神经网络较强的泛化能力使其能够处理复杂的、非线性的六自由度机械臂逆运动学问题。

（3）在MATLAB环境下实现了BP神经网络对机器人逆运动学求解，通过仿真实验对比粒子群优化算法对BP神经网络性能的影响可知，相比于传统BP神经网络，PSO-BP神经网络在机器人逆运动学求解中的精度更高、求解速度更快。

参考文献：

[1]龚闯，戴程浩，江维，等.基于改进A*算法的大型织机车间运载机器人路径规划[J].纺织工程学报，2023， 1（2）：57-67.

GONG Chuang， DAI Chenghao， JIANG Wei， et al. Path planning of transport robot in large loom workshop based on improved A* algorithm[J].Journal of Advanced Textile Engineering， 2023， 1（2）：57-67.

[2]邹亮，吴晓，袁勤政.一种自动循迹 AGV 平台机械结构设计及力学分析[J].武汉纺织大学学报，2023， 36（5）：53-57.

ZOU Liang， WU Xiao， YUAN Qinzheng. Mechan- ical structure design and mechanical analysis of an automatic tracking AGV platform[J]. Journal of Wuhan Textile University，2023， 36（5）：53-57.

[3]陳家浩，庞爱民，李浩，等.仓储立体库纱锭智能配重打包方法研究[J].武汉纺织大学学报，2022， 35（5）：46-50.

CHAN Jiahao， PANG Aimin， LI Hao， et al. Re- search on the method of intelligent weighing and packing for three-dimensional warehouse[J]. Jour- nal of Wuhan Textile University， 2022， 35（5）：46-50.

[4]李进，方楚桥，王绍祥，吴晓.自动穿经机上轴车改造设计[J].纺织工程学报，2023，1（2）：90-96.

LI Jin， FANG Chuqiao， WANG Shaoxiang， WU Xiao. Reconstruction design of upper axle trolley of automatic drawing- in machine[J]. Journal of Wuhan Textile University， 2023， 1（2）：90-96.

[5]SARIYILDIZ E， CAKIRAY E， TEMELTAS H. A comparative study of three inverse kinematic methods of serial industrial robot manipulators in the screw theory framework[J]. International Jour- nal of Advanced Robotic Systems， 2011， 8（5）：9-24.

[6]李宪华， 盛蕊， 张雷刚， 等.六自由度模块化机器人手臂奇异构型分析[J].农业机械学报， 2017， 48（7）：376-382.

LI Xianhua， SHENG Rui， ZHANG Leigang， et al. Singular configuration analysis of 6-DOF modular manipulator[J]. Transactions of the Chinese Soci- ety for Agriculture Machinery， 2017， 48（7）：376-382.

[7]姜宏超， 刘士荣， 张波涛.六自由度模块化机械臂的逆运动学分析[J].浙江大学学报（工学版）， 2010， 44（7）：1348-1354.

JIANG Hongchao， LIU Shirong， ZHANG Botao. Inverse kinematics analysis for 6 degree-of-free- dom modular manipulator[J]. Journal of Zhejiang University（Engineering Science）， 2010， 44（7）：1348-1354.

[8]TATUM R， LUCAS D， WEAVER J， et al. Geomet- rically motivated inverse kinematics for an arm with 7 degrees of freedom[C]//IEEE.Proceeding of OCEANS 2015- MTS /IEEE.Washington： IEEE， 2015：1-6.

[9]卢喆， 郑松.基于几何法和旋量理论的6自由度机器人逆解算法[J].机械传动， 2017， 41（6）：111-114.

LU Zhe， ZHENG Song. Inverse kinematics algo- rithm of 6-DOF robots based on geometric meth- od and screw theory[J]. Journal of Mechanical Transmission， 2017， 41（6）：111-114.

[10]王国勋， 舒启林， 王军.基于旋量理论的6R工业机器人运动学建模与分析[J].机床与液压， 2018， 46（23）：35-42.

WANG Guoxun， SHU Qilin， WANG Jun. Kine- matics modelling and analysis for 6R industrial robot based on screw theory[J]. Hydromechatron- ics Engineering， 2018， 46（23）：35-42.

[11]林贞国.挖掘机器人轨迹规划与仿真研究[D].太原：太原科技大学， 2017.

LIN Zhenguo， Research on trajectory planning simulation of excavator robot[D]. Taiyuan：Taiyu-an University of Science and Technology， 2017.

[12]PAUL R P， SHIMANO B， MAYER G. Differen- tial kinematics control equations for simple ma- nipulators[J]. IEEE Transactions on Systems，Man and Cybernetics， 1981， 11（6）：456-460.

[13]BIDOKHDI H S， ENFERADI J. Direct kinemat-ics solution of 3-R R R robot by using two differ- ent artificial neural networks[C]//IEEE. Proceed- ings of 20153rd RSI International Conference on Robotics and Mechatronics （IC ROM）. Teh- ran： IEEE， 2015.

[14]陈睿， 闵华松.基于BP和RBF神经网络的机器人逆运动学算法[J].机床与液压， 2019， 47（23）：22-27.

CHEN Rui，MIN Huasong. Inverse kinematics al- gorithm of robot based on BP and RBF neural networks[J]. Hydromechatronics Engineering， 2019， 47（23）：22-27.

[15]董慧芬， 高爽笑， 宋金海.基于径向基神经网络的Delta机器人位置精度补偿[J].科学技术与工程， 2020， 20（31）：12883-12889.

DONG Huifen， GAO Shuangxiao， SONG Jinhai. Position accuracy compensation of delta robot Based on RBF neural network composites[J]. Sci- ence Technology and Engineering， 2020， 20（31）：12883-12889.

[16]陈平， 刘国海.基于 RBF 神经网络的 MOTO- MAN-UPJ 型机器人运动学逆解[J].机床与液压， 2006（12）：72-74.

CHEN Ping， LIU Guohai. A method for solving inverse kinematics of MOTOMAN-UPJ manipu- lator based on RBF network[J]. Hydromechatron- ics Engineering， 2006（12）：72-74.

[17]杨萍， 刘晓琴， 张淑珍.基于BP网络的水轮机修复专用机器人运动学逆解分析[J].机械设计， 2005（6）：36-38.

YANG Ping， LIU Xiaoqin， ZHANG Shuzhen. In- verse kinematic solution analysis of a special ro- bot for hydraulic turbine repair based on BP net- work[J]. Mechanical Design， 2005（6）：36-38.

[18]石建平， 李培生， 劉国平， 等.基于改进克隆选择算法的机械臂运动学逆解[J].计算机集成制造系统， 2021， 27（10）：2929-2939.

SHI Jianping， LI Peisheng， LIU Guoping， LIU Peng. Inverse kinematics of manipulator based on improved clonal selection algorithm[J]. Com- puter- Integrated Manufacturing Systems， 2021，27（10）：2929-2939.

[19]董云， 杨涛， 李文.基于解析法和遗传算法的机械手运动学逆解[J].计算机仿真， 2012， 29（3）：239-243.

DONG Yun， YANG Tao， LI Wen. Algorithm based on analytical method and genetic algo- rithm for inverse kinematics of redundant manip- ulator[J]. Computer Simulation. 2012， 29（3）：239-243.

[20]陈睿， 闵华松.基于BP和RBF神经网络的机器人逆运动学算法[J].机床与液压， 2019， 47（23）：22-27.

CHEN Rui， MIN Huasong. Inverse kinematics al- gorithm of robot based on BP and RBF neural networks[J]. Hydromechatronics Engineering， 2019， 47（23）：22-27.

[21]BEHNAMIAN J， GHOMI S M T F. Develop- ment of a PSO- SA hybrid metaheuristic for a new comprehensive regression model to time-se- ries forecasting[J]. Expert Systems with Applica- tions， 2010， 37（2）：974-984.

[22]EBERHART R C， SHI Y. Comparing inertia weights and constriction factors in conference particle swarm optimiation[C]//IEEE. Congresson Evolutionary Computation. Piscataway， IEEE， 2000：84-88.

[23]BIDOKHTI H S， ENFERADI J. Direct kinemat- ics solution of 3-R R R robot by using two differ- ent artificial neural networks[C]//IEEE. Proceed- ings of 20153rd RSI International Conference on Robotics and Mechatronics （IC ROM）. Teh- ran： IEEE， 2015.

[24]芮宏斌， 曹伟， 孙宁宁.基于BP神经网络的光伏阵列清洁机械臂逆运动学分析与时间最短运动规划[J].太阳能学报， 2022， 43（10）：43-51.

RUI Hongbin， CAO Wei， SUN Ningning. In- verse kinematics analysis and tine opimal motion planning of photovoltaic array cleaning manipu- latory based on BP neural neteork[J]. Acta Ener- giae Solaris Sinica， 2022， 43（10）：43-51.

[25]周帅， 刘晓鸣.基于神经网络的工业机器人力控制研究[J].机床与液压， 2023， 51（17）：21-25.

ZHOU Shuai， LIU Xiaoming. Research on force control of industrial robot based on neural net- work[J]. Hydromechatronics Engineering， 2023， 51（17）：21-25.

（责任编辑：孙婷）