基于优化变分模态分解的人体生命信号分离与重构方法研究

文显琼，王鑫瑜，石 丁，张 坤

（1.西安培华学院智能科学与工程学院，西安 710125；2.西安工业大学电子信息工程学院，西安 710032；3.空军第986 医院医学工程科，西安 710054）

0 引言

心跳和呼吸是反映人体生命状态的重要参数，方便、快速、准确地检测出心跳和呼吸信号无论是对健康评估还是疾病检测都至关重要。目前的心跳、呼吸信号检测方式仍然以接触式为主，而生命探测雷达可以在隔一定距离、穿透一定障碍物的条件下检测人体生命信号。生命探测雷达的工作原理是雷达发射电磁波隔一定距离或穿透障碍物照射到人体，发射的电磁波加载了人体心跳、呼吸等生命信号后反射回来被雷达接收、解调从而实现信号检测。雷达生命探测技术具有非接触的特点，即无需任何传感器、电极的连接，因此适用于烧烫伤患者、传染患者、新生儿等特殊人群的生命体征检测[1-3]。

基于以上优点，雷达生命探测技术被越来越多的团队研究并取得了一定的成果。2004 年，来自瑞士的Michahelles 等[4]对使用雷达探测人体生命体征进行了相关研究，然而在被试者自由呼吸的情况下，探测设备无法精准地获取到其心跳信号。相关研究[5-7]采用小波变换的方法进行人体生命信号的提取，该方法适合处理瞬时信号，但是算法复杂、实时性较差、自适应能力不强。文献[8]基于经验模态分解（empirical mode decomposition，EMD）将雷达接收信号分解成有限个本征模态函数（intrinsic mode function，IMF），再将IMF 分量从时域上重构心跳与呼吸信号。但该方法存在模态混叠现象，不能有效地提取心跳信号。以上研究表明，该领域目前仍存在一些困难和挑战，主要包括检测环境中的强背景噪声以及人肢体运动干扰等，这些会影响心跳和呼吸信号的准确提取与重构。完全噪声辅助聚合经验模态分解（complete ensemble empirical mode decomposition with adaptive nosie，CEEMDAN）算法是在EMD 算法基础上改进的一种方法，由于其具有多尺度特性，因此适用于包含生命体征信息的非平稳雷达信号的检测[9-10]。但是该方法一般需要对同一区域进行持续的较长时间观察，才能较精确地重构人体生命信号，此时雷达采集的数据会达到GiB 量级，因此在计算极值点包络以及筛选和更迭模态条件时需要更多时间，这会导致运算效率低下。在实际的灾后救援中，“时间就是生命”，快速、准确地探测才能挽救更多生命，因此亟须研究一种高效而准确的生命信号提取分离方法。针对上述问题，本文提出一种基于优化变分模态分解（variational mode decomposition，VMD）的人体生命信号分离与重构方法。

1 基于VMD 的人体生命信号分离与重构

首先，将VMD 处理得到的各IMF 与人体生命信号之间的最大相关性作为适应度函数，采用粒子群优化（particle swarm optimization，PSO）算法对其进行参数优化；然后采用优化VMD 将雷达回波信号分解为一系列的IMF，并计算出每个IMF 的归一化排列熵值；最后比较各排列熵和设定的排列熵阈值Hthreshold，去除大于Hthreshold的噪声分量，基于剩余的IMF分量重构出人体生命信号。

1.1 VMD

VMD 是一种具有自适应、完全非递归特性的模态变分与信号处理方法[11]，其主要特点是寻找并匹配各个模态的中心频率及有效带宽，将IMF 进行有效分离，进而得到变分问题的最优解。在本文中，将人体生命信号s（t）分解成K个IMF 分量vi（t），并确保各分量的估计带宽之和最小，上述过程可以表示为

式中，i为序号；t为时间变量；vi（t）为第i个IMF；ωi为第i个IMF 的中心频率；∂t表示对时间变量t求偏微分；δ（t）为狄利克雷函数；s为原始信号。在高斯噪声环境下，二次惩罚因子α 确保了信号重建的准确性，拉格朗日乘子λ（t）则可以保证约束条件的严谨性，通过引入2 个算子，可以将公式（1）的约束性问题转变为非约束性问题，推广到拉格朗日表达式如公式（2）所示：

虽然VMD 相较于传统EMD 具有较好的去噪效果和较快的运算速度[12]，但参数设置不当可能会导致成分丢失或模态混叠。若分解层数K值过小会产生IMF 混叠，过大则信号会被过度分解；如果二次惩罚因子α 的取值过大，则各IMF 频带过窄，会导致有用信息丢失，而取值过小则IMF 频带过宽，会导致其他干扰成分的进入。上述分析表明仅凭经验手动设置参数K和α 很难达到最佳分解效果。

1.2 基于PSO-VMD 的生命信号分离方法

PSO 是一种基于进化原理的算法，通过迭代比较适应度函数区域中单个粒子的最优状态和全局最优状态来调整粒子对环境的适应度，进而在该区域中找到最优解。在对VMD 参数进行优化时，选择合适的适应度函数是PSO 平稳运行的关键。不同的α与K参数组合往往会导致VMD 分解的IMF 分量出现不同程度的伪影，这些伪影的强弱程度可以通过比较每个IMF 和人体生命信号之间的相关系数来评估，并通过计算这些相关系数的总体均值来进行量化。以第i个IMF 与人体生命信号的相关系数Ri为例，其计算公式如下：

式中，T表示信号采集时长。IMF 与人体生命信号的相关系数均值以公式（7）表示：

式中，K表示分解后的IMF 个数。为了防止个别参数组合下相关系数出现大幅波动，本方法还结合相关系数的方差指标，以相关系数均值与方差的比值作为适应度函数Ff对VMD 参数进行优化，如公式（8）所示：

当使用PSO 优化VMD 参数时，先初始化参数，然后基于采集的人体生命信号，分别在[200，2 000]与[1，8]的范围内遍历迭代优化参数[α，K]。图1 描绘出适应度函数在不同[α，K]组合下的分布情况，图中红色虚线标出的点即为寻优结果。由图1 可知，当α=943、K=4 时，由VMD 分解的IMF 中包含的伪影分量最小，与人体生命信号的相关性最强，最大互相关值为18.27。

图1 PSO 迭代寻优结果

1.3 基于排列熵的生命信号重构方法

由于部分IMF 的中心频率位于主噪声频带内，这给噪声的准确分离带来了困难。排列熵可以通过检测时间序列的随机性来衡量信号包含多少噪声，因此可以使用排列熵来定量评估每个IMF 中的噪声程度，并根据设置的熵阈值自动识别和去除高噪声IMF。对长度为N的时间序列v（i）展开相空间重构，从而获得重构矩阵Y：

式中，m为嵌入维数；τ 为延迟时间；K=N-（m-1）τ。矩阵Y中共有K个重构分量，每一行为一重构分量。按升序排列重建矩阵中的第j个分量[v（j），v（j+τ），…，v（j+（m-1）τ）]，并将重新排序后的分量中每个元素的新列索引标示如下：

在重新排列后，就构成了一个符号序列的集合S（l）：

式中，l=1，2，…，k，k≤m！。将每个符号序列的出现次数除以总次数m！来计算每个符号序列的出现概率，记作P1，P2，…，Pk。时间序列v（i）中的k种不同符号序列的熵值定义为

使用公式Hpe=Hpe/lg（m！）将熵值归一化至[0，1]。熵值表示的是时间序列的随机性，熵值越大表明该序列为噪声的可能性就越大。因此，选择合适的排列熵阈值是去除噪声的关键，是保证人体生命信号准确重构的基础。根据文献[13]的结论和多次测试实验研究了时间序列的随机性与其对应熵值之间的线性关系，发现设置m=6、排列熵阈值Hthreshold处于0.78～0.8 之间可最大程度去噪。本文将熵值Hpei＞0.8 的IMF 去除，并根据保留下来的各IMF 重构人体生命信号。基于优化VMD 和排列熵的人体生命信号重构算法流程图如图2 所示。具体实施步骤如下：

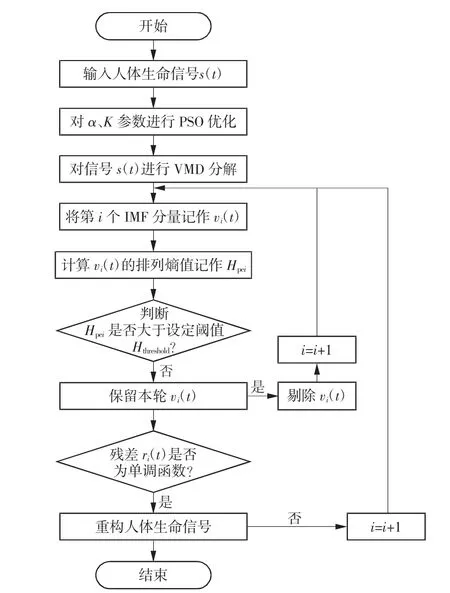
图2 PSO-VMD 算法流程图

（1）利用各IMF 与人体生命信号的最大相关性作为PSO 的适应度函数，进行VMD 参数优化；

（2）采用优化的VMD 对雷达回波信号s（t）进行处理，分解为一系列IMF 分量vi（t）；

（3）计算各vi（t）的排列熵值Hpei，将排列熵值归一化到[0，1]区间；

（4）将每个vi（t）的熵值与设定的阈值进行比较，去除大于阈值的高噪声vi（t），并根据剩余残差ri（t）重构出人体生命信号。

2 性能验证试验

为了验证本文提出的方法的性能，进行了雷达人体生命信号采集和处理实验。采用超宽谱（ultrawideband，UWB）雷达（X4m200，中心频率为7.29 GHz，带宽为1.4 GHz）对6 名（2 名男性和4 名女性）年龄在23～45 岁的成年受试者以卧姿平躺的姿态进行非接触生命信号采集。采集中将UWB 雷达置于距离受试者体表约1 m 处正对人体胸部，人体目标与雷达之间无障碍物遮挡，每位受试者在早、中、晚不同时间点各采集10 组数据，合计60 组数据，单次数据采集时间为30 s。

以采集到的人体生命信号s′（t）为输入，为了模拟环境噪声和肢体抖动引起的干扰，向s′（t）中加入均值为0、方差为σ=6 的高斯白噪声randa（0，σ），构建雷达回波信号s（t），表示为

采用PSO-VMD 对构建的雷达回波信号s（t）进行分解，结果如图3 所示。可以看出，通过分解，人体生命信号和噪声得到了有效分离，并且成功提取出了分别代表雷达呼吸和心跳信号的IMF1 与IMF2 分量。

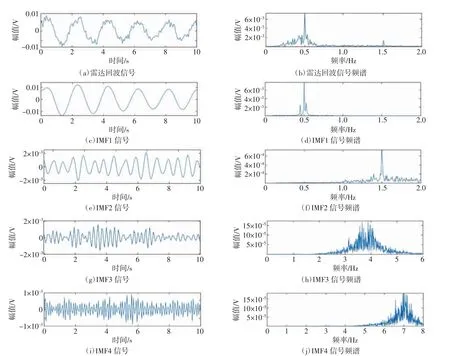
图3 PSO-VMD 算法分解结果

为实现自动去噪，计算分解后的每个IMF 归一化排列熵值可得：Hpe1=0.316 5、Hpe2=0.543 1、Hpe3=0.825 3、Hpe4=0.903 6。去除Hpei＞0.8 的IMF3 与IMF4分量，将剩余IMF 重构。

本文将未行参数优化的VMD、CEEMDAN 和PSO-VMD 的性能进行了比较，雷达回波信号以及分别采用3 种方法重构的人体生命信号时域、频域结果如图4 所示。可以看出，经过3 种方法重构，噪声均得到了降低，信噪比（signal-to-noise ratio，SNR）均得到了提升。从时域结果上看，CEEMDAN 和PSO-VMD效果优于VMD，而PSO-VMD 对心跳成分的保留能力更强。从频域结果上看，基于排列熵的PSO-VMD重构对除呼吸、心跳主峰外的频谱成分抑制能力最强，对心跳主峰提取效果最好。

图4 雷达回波信号以及3 种方法重构的人体生命信号时域、频谱图

本文还在多种噪声水平下（噪声方差σ 处于[1，10]）对所提出的方法与无限脉冲响应（infinite impulse response，IIR）滤波、未行参数优化的VMD 以及CEEMDAN 的性能进行了比较，通过加入不同能量水平的高斯白噪声，从SNR和均方根误差（root mean square error，RMSE）2 个方面来评价各方法的性能。SNR 和RMSE 分别定义为

式中，s（i）表示原始信号；s2（i）表示原始信号的平方；s¯（i）表示s（i）的平均值；N表示信号s（i）的长度。图5 为各方法对添加不同能量水平的高斯白噪声信号的处理结果。

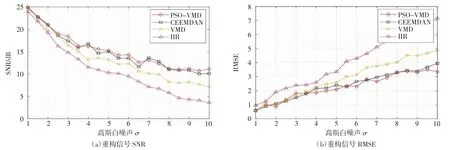
图5 不同噪声水平下4 种方法重构信号的SNR 和误差分析结果

此外，本文还采用IIR、VMD、CEEMDAN 和PSOVMD 4 种方法对采集的60 组雷达数据（噪声水平σ=6）进行处理，并计算每种方法处理后的SNR 和RMSE，得到的SNR 分别为（8.96±0.83）dB、（12.33±1.26）dB、（13.10±1.01）dB、（14.10±0.80）dB，RMSE 分别为4.35±0.25、3.16±0.27、2.64±0.21、2.34±0.16。

从图5 可以看出，在SNR 和RMSE 2 项性能指标上，在不同噪声水平下，4 种方法的SNR 均随着的增加而降低，RMSE 则随着σ 的增加而增加，总体上PSO-VMD 性能最优，IIR 最差。由于传统的IIR 数字滤波方法不能自适应地去除通带内的噪声分量，所以该方法分离出的人体生命信号往往与噪声分量混合，从而导致其信噪比最低。当高斯白噪声σ 达到最高水平10 时，IIR 数字滤波处理后信号的RMSE为7.03，而PSO-VMD 处理后的RMSE 结果为3.35，说明PSO-VMD 在高噪声信号处理上具有优势，重构的信号误差最小，最接近于人体生命信号。虽然CEEMDAN 方法在SNR 和RMSE 上均与PSO-VMD相近，但其存在着处理时间过长的问题。

图6为CEEMDAN 和PSO-VMD 2 种方法在处理30～600 s 信号采集时长的信号时所需处理时长的统计结果。随着信号采集时长的增加，CEEMDAN方法的运行时长呈线性增长，在处理600 s 的时长信号时，CEEMDAN 需要10.41 s，这比PSO-VMD 方法（1.62 s）多用了8.89 s，如将该方法应用于嵌入式设备时则需要更长时间。相比而言，PSO-VMD 具有更好的运算实时性，更有利于嵌入式系统的集成。综上，PSO-VMD 的实际性能优于其他处理方法，通过融合排列熵阈值，能有效去除噪声，从雷达回波信号中准确分离并重构人体生命信号。

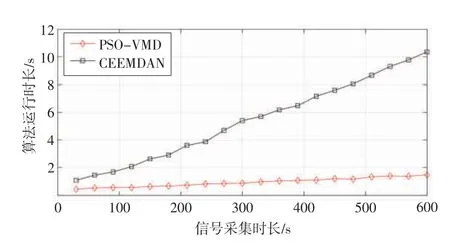
图6 针对不同时长信号2 种方法所需处理时长的对比结果

3 结语

本文提出了一种基于排列熵的PSO-VMD 生命信号分离与重构方法，用于非接触检测生命体征，成功实现了在复杂噪声条件下对人体生命信号的重构和心跳、呼吸信号的自动分离。雷达实测数据的处理结果显示，PSO-VMD 在重构信号的SNR、RMSE 以及处理时长等指标上均优于IIR、VMD、CEEMDAN方法，表明了该方法在烧烫伤患者、传染患者、新生儿等特殊群体的生命体征非接触检测领域具有很好的应用前景。本文提出的方法以较高的精度实现了不同噪声水平下的人体生命信号重构，但是在信号采集时仅采用了平躺的姿态，这对于灾后废墟掩埋伤员搜救和临床监护都存在不足，后续还需进行更多姿态的信号采集实验，以进一步提升该方法的适用性。