三级反射式智能聚光塔仿真实验教学设计与改革
2024-05-15张晟国谢广明杜玉红
赵 地,张晟国,谢广明,杜玉红
(1.天津工业大学a.工程教学实习训练中心;b.创电子与信息工程学院;c.创新学院,天津 300387;2.北京大学工学院,湍流与复杂系统国家重点实验室,北京 100871)
0 引言
目前反射式聚光器通常采用曲面玻璃(背面镀银)或曲面镀膜铝板制成,其反射系数可达95%以上。但聚光镜场仍存在着聚光损失高、经济性不佳的问题[1-2]。通过布置优化,多级反射式反射镜的镜场效率分别达到71.46%和73.6%,均高于单级反射式镜场,并且两个镜场的占地面积也都远小于单级反射式镜场,说明多级反射式反射镜具有更优的镜场性能。因此,本实验带领学生进行光电系统设计,设计一套追光与聚光性能优良,系统稳定性强的智能反射式聚光塔,通过系统设计、镜场搭建、实验仿真、算法验证,探索光电控制系统设计的实验教学改革。
1 系统整体设计
实验对传统低效率的光伏发电模式做出改进,设计一种新型聚光式发电塔。通过北斗追光算法,根据地理参数得出太阳的空间位置,双轴轨迹追踪可以使反射光正确地反射在光伏电板上,通过加入模糊逻辑控制PID算法,保证系统的稳定性。三级反射式镜场聚光使得光照的利用进一步增强。随着太阳的移动,通过高精度、高可靠性定位系统,实现反射镜的自动跟踪,保证了发电的充足。同时,塔式结构使空间高度与面积交复利用以节约占地面积,降低成本[3-5]。
2 三级反射镜场结构设计
传统单级反射式聚光方式简单[6],如图1 所示。槽式和碟式热发电系统在太阳跟踪过程中,聚光镜采光口径能够始终垂直于太阳光,以使入射光线汇聚到焦线(槽式)或焦点(碟式)处的吸热器中[7]。但是一级反射存在重大的光能损失,在一级反射中,反射镜采光口径无法做到太阳光垂直,一级反射在对太阳光反射聚焦时会产生一个入射角,这样造成反射镜在口径内接收到的有效辐射能要小于光线垂直入射时的能量[8-9]。在接近日落日出的时段以及镜场边缘的反射镜,太阳光入射角非常大,此时反射镜所能采集到的太阳辐射能大大减少(见图2)。
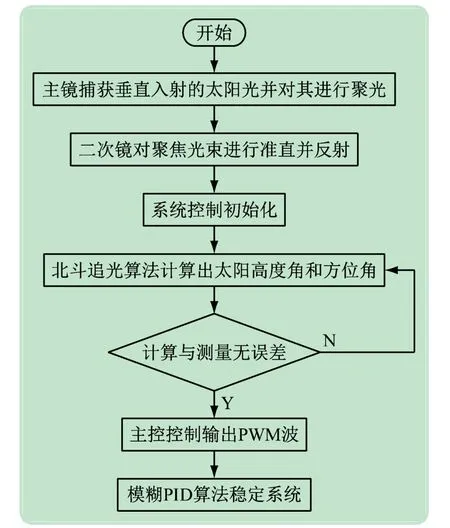
图1 系统硬件设计框图
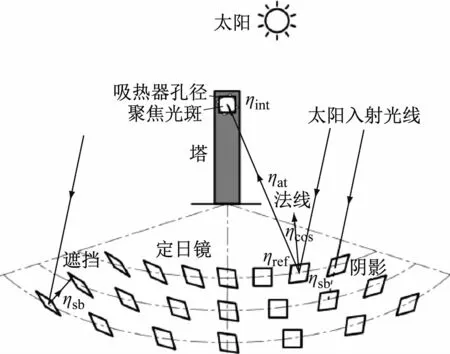
图2 一级反射式聚光塔
研究证明,余弦损失是镜场最主要的光学损失,占到总损失的48.7%。为了规避余弦损失,本实验采用三级反射聚光结构。
系统首先通过一次镜即主镜来捕获垂直入射的太阳光并对其聚焦,二次镜对聚焦光束进行准直并反射,提高光束的能流密度,三次镜对二次镜准直后的光束进行反射,最终投射到发电装置。一次镜和二次镜的焦点保持一致,一次镜的孔径垂直于太阳入射光,这样避免了余弦效应的产生。本系统中二次镜和主镜相对固定,二者焦点一致。三次镜由舵机驱动可绕其中心做两自由度转动将光束反射到发电装置上,它仅改变光束的传播路径,不会改变光束的能流密度分布特性。
考虑到太阳入射光束近似平行,实验首先基于几何光学理论提出了采用旋转抛物面型的一次镜和二次镜,平面三次镜用来改变光束传播路径,如图3 所示。与一次镜共焦的二次镜能够将焦点发出的光线平行反射到目标平面上。
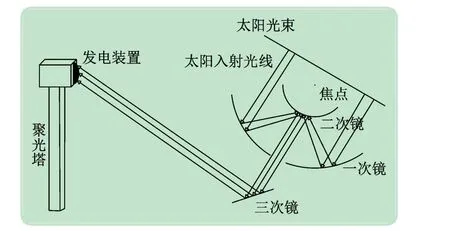
图3 三级反射镜场结构示意图
在三级反射式聚光方案下,团队设计的反射镜按照光学理论,计算镜场的各个参数,利用光学效率计算模型对传统的单级反射式聚光镜场进行求解,比较镜场各项损失对光学性能的影响程度,在此基础上对镜场进行Tracepro光路仿真验证,完成三级反射聚光结构的设计,如图4 所示。

图4 三级反射聚光镜场3D结构图
3 算法设计
3.1.1 北斗追光算法
本实验建立天体坐标系[10],计算出太阳高度角和方位角。首先,计算磁偏角,时角和天顶角。接着接受北斗传输的纬度,计算出太阳的方位角和高度角。通过查阅资料可得太阳赤纬的精准值,适用于1901~2099 年。其计算公式为:
取实际回归年长度为365.242 2 天,取1985 年为标准年。以标准年为基础计算日地夹角:
将式(4)中的日地夹角代入式(1)计算得太阳赤纬,之后再计算太阳时角:
将数据代入公式计算太阳高度角h和方位角φ:
式(1)~式(6)中:N为积日;δ 为赤纬角;ω 为太阳时角;ST为真太阳时;h为太阳高度角;φ为当地维度;φ为太阳方位角;K为春分日积日。
3.1.2 镜面法向计算
聚光算法需要精准的计算三次镜的移动,太阳能滴胶板竖直放置于H的高度[11]。得到光源的角度后,根据不同的镜面位置,计算各自的法向角度。假设各个镜面为质点,高度为0,横坐标为xi,纵坐标为yi,镜面方向角度分别设为φi、hi,将光源方位角φ转换为以正北方起顺时针计量φ0,太阳高度角h0不变,光线在滴胶板上的坐标为(Xi,Yi)。根据空间几何关系计算得到:
建立非线性规划的数学模型,输入设定为φi和hi,输出设定为,确定各参数的约束范围。通过梯度下降算法,计算出最优输入,同时得到最佳反射光线的矢量形式。
在三维空间中,光线为平面内的二维关系,但三维空间的坐标转换复杂,因此采用二维空间的矢量形式计算后,推广至三维空间使用。假设镜面为理想反射镜,其折射率n为1,出射介质的折射率n′为-1。B和θ′分别为反射光单位矢量和反射角,N 为镜面法向量。其中的计算关系如下:
将已知的入射光和最佳反射光矢量代入以下公式,即可算出最佳镜面法向量(见如图5):
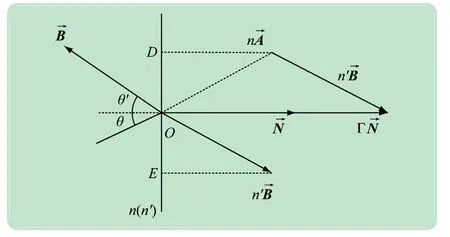
图5 镜面法向模型
3.1.3 模糊PID算法
本实验将步进电机转动角度作为输出值,计算得到的高度角和方位角为期望值,光电传感器获得实际值。在实际应用中,为了更方便地对数据进行处理,将PID算法离散化得:
对方位角和高度角分别进行PID 控制,双轴控制云台,精准反射太阳光线。由于存在天气复杂多变的情况,传统PID 难以实时改变参数,无法适应当前模型[12-14]。为了解决这个缺点,本实验系统引入模糊控制器。模糊控制分为三大模块:输入模糊化,模糊推理,输出清晰化。使其精度更高,更贴合实际,见图6。
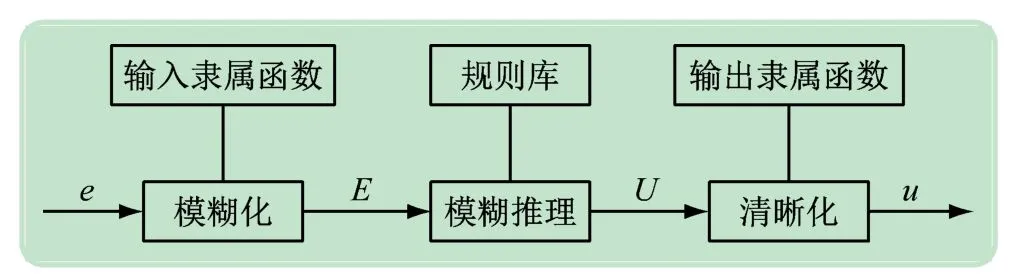
图6 模糊PID算法逻辑
采用工业软件Matlab 联合Simulink 进行仿真实验,获取太阳方位角和高度的实时位置。通过传感器反馈,比较实际值与期望值得到差值err,实时计算调整输出参数。同时,采用二维输入,E、EC,三维输出kp、ki、kd,如图7 所示。
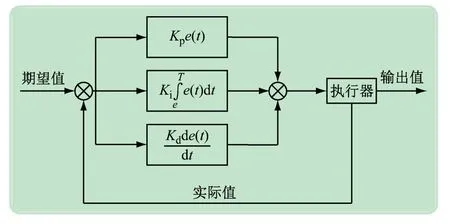
图7 模糊PID算法计算
规划输入与输出的论域和三角形隶属函数,划分各输入量的模糊区间,建立推理规则库,Kp、Ki、Kd的规则库如表1~3 所示。通过大量仿真获取实验数据,在系统中引入模糊控制器使其适用于复杂的风噪环境,极大提高了系统的适用范围。
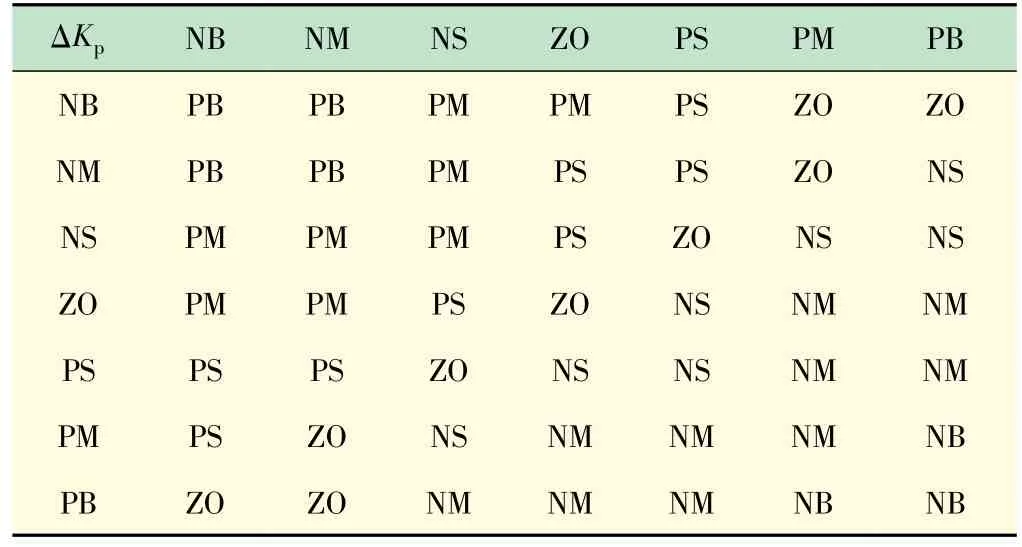
表1 参数ΔKp 的模糊规则库
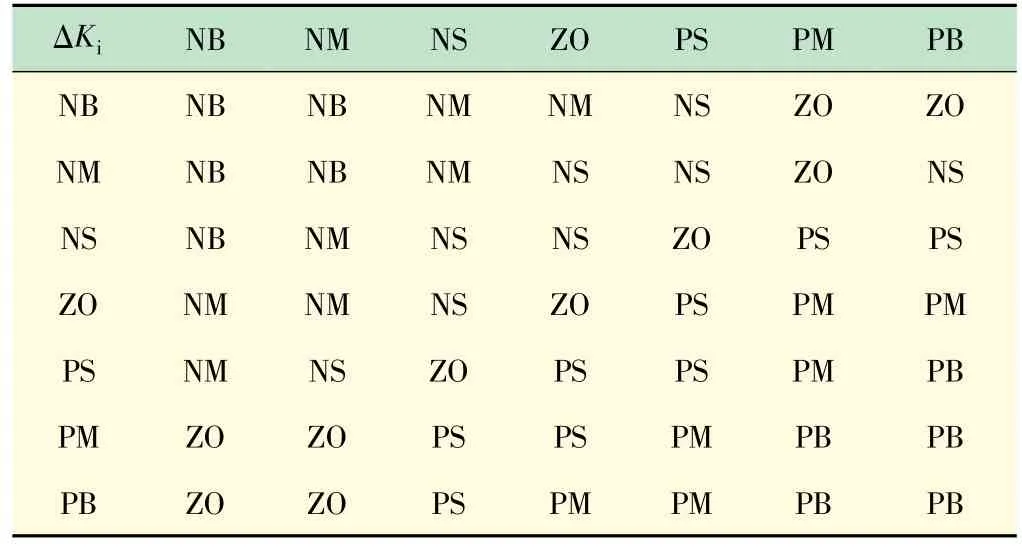
表2 参数ΔKi 的模糊规则库
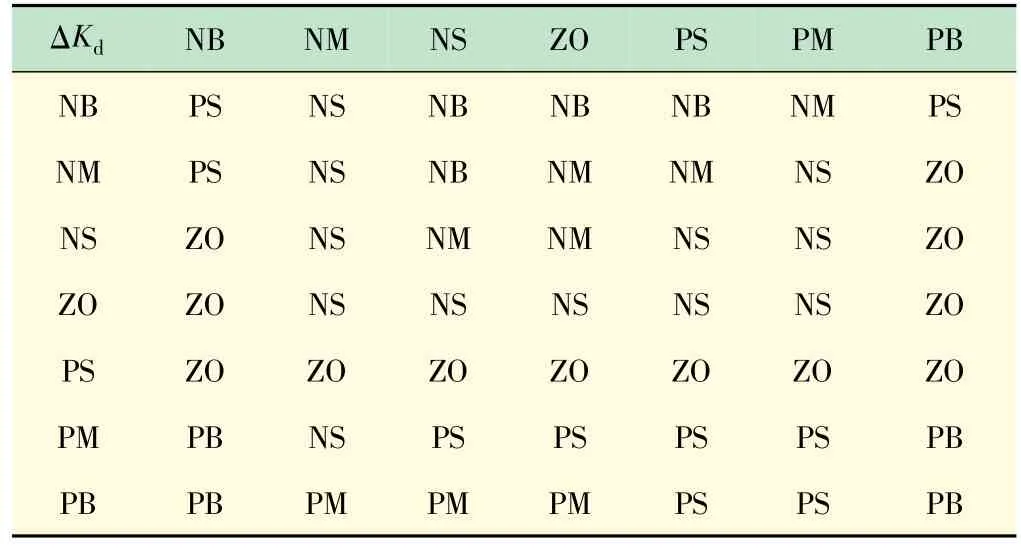
表3 参数ΔKd 的模糊规则库
4 实验结果和分析
4.1 实验目的
本实验的目的是找到准确率高、收敛速度快的追光算法、鲁棒性强的PID 算法。通过搭建三级反射式镜场,实现对太阳能的高效利用。
4.2 实验结果与分析
根据长时间测试,在日出日落个别特殊时间,太阳方位角有较大的误差,其他时间段太阳角度计算值和实际数据吻合良好,大部分误差在1%以内,如图8、9所示。北斗算法的光线利用率绝大部分时间都在90%以上,如图10 所示。验证了计算方法正确可行并且精准度较高。
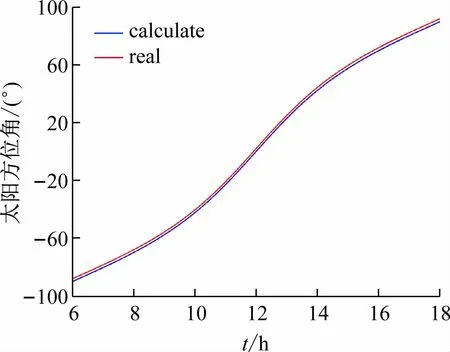
图8 太阳方位角实测与计算曲线对比
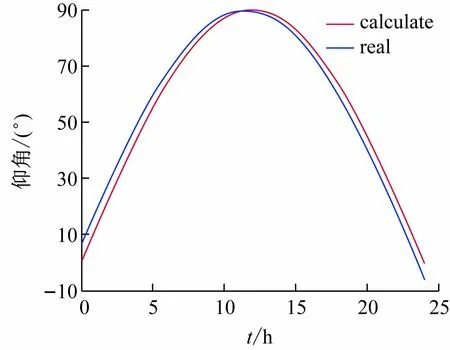
图9 太阳高度角实测与计算曲线对比
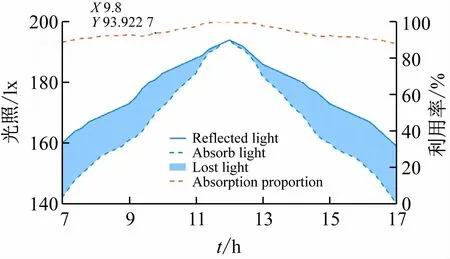
图10 北斗追光算法光线利用率曲线
用MATLAB联合Simulink对PID算法进行数据分析;大量仿真表明模糊PID曲线光滑平稳,鲁棒性强,绝对误差和收敛时间都优于普通PID,如图11 所示。
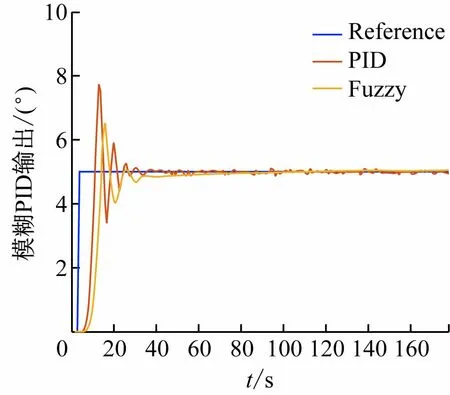
图11 两种PID算法对比
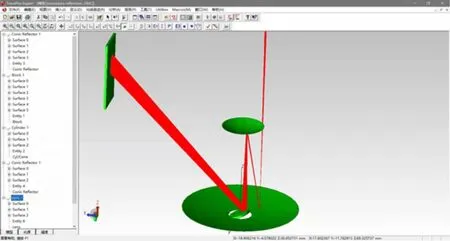
图12 Tracepro光线仿真
实验在太阳仿真的模拟环境下,考虑太阳非平行光照射的情况,以太阳的运动规律及反射镜的反射模型为基础,采用Tracepro 对北斗追光算法进行光学路线仿真,如果数据量较少,难以对全过程进行合理的分析评价[15],因此本文对20 个时间点采样,记录下对应的光线数据,使用重心拉格朗日插值法,并结合分段插值法进行计算。同时为防止产生龙格效应震荡,使用切比雪夫节点进行采样,分析与改进了太阳张角对截断效率的影响,通过计算接收器表面的辐照度分布和总光通量,发现聚光性等性能可以提高16%~19%。
5 结语
实验设计涉及机械、光学、电路以及控制等学科,功能扩展性好,实用性高,是光电控制系统设计的创新实验教学改革。从北斗追光算法、三级镜场的设计、模糊PID算法等方面阐述了系统的设计思路,通过对比仿真实验验证算法的鲁棒性以及系统聚光性能的提升,引导学生通过改进算法,设计新的多级反射式镜场来提高太阳能发电效率,探索提升系统聚光性能的实验教学方法。
