坝基混凝土防渗墙损伤开裂数值模拟研究

2024-05-15祁伟强李秀文

中国水能及电气化 2024年4期

祁伟强张高李秀文

(1.中国电建集团贵阳勘测设计研究院有限公司，贵州贵阳 550081；2.中国水利水电科学研究院，北京 100038)

混凝土防渗墙不仅能适应各种构造型式的坝体，也能适应各种复杂坝基，并具有抗渗性能强、运行安全可靠、后遗症少、使用寿命长等优点，在水利水电工程中得到了广泛应用，发挥了良好的效益[1]。防渗墙的安全性通常是整个工程安危的主要控制因素之一，而且防渗墙本身也存在着一些缺点，因此，如果防渗墙设计不当，不能充分考虑到墙体的受力状况，那么防渗墙在竖向荷载和水平荷载的作用下，其所受应力很有可能超过防渗墙所用材料的抗压强度或者抗拉强度，从而导致裂缝的产生。裂缝[2-5]，尤其是贯穿裂缝一旦产生，防渗墙的防渗功能就急剧下降，整个坝体就很容易发生管涌、流土等水力破坏，威胁到大坝的安全。所以混凝土防渗墙对土石坝的安全是至关重要的，一旦失事，土石坝会出现严重的安全隐患。

目前对防渗墙开裂情况的研究较少[6-8]。由于坝基不均匀沉降、地震等因素，高土石坝坝基混凝土防渗墙可能会产生规模不等的裂缝，这样势必会对坝基的渗流和稳定产生严重的影响，甚至会威胁整个工程的安全。但是目前对此研究的较少，且研究结果相差较大。本文采用Bathe本构模型和D-P Cap模型对坝基防渗墙的损伤开裂特征进行研究，并结合部分实测资料进行对比。

1 本构模型

1.1 Bahte本构模型

该混凝土模型的基本特征包括[9]：

a.Bathe模型可以考虑拉坏、压碎，包括应变软化后的破坏特性。

b.参数较多，但基本由单向拉压试验参数确定。

c.可以指定多轴应力状态下的破坏包络线，共六条，用当量的方式表示，也可以使用常用的其他破坏准则。

d.每个单元积分点的历史变量达20多个，如应力峰值，当前应力应变、加载卸载状态等。

e.不同的应力水平，自动切换各向同性硬化和正交各向异性硬化。

f.单元破坏后先对开裂面进行判别，在其基础上对单元的法、切向刚度进行修正。

图1为Bathe模型双轴破坏包络线，图2为三轴破坏包络线。

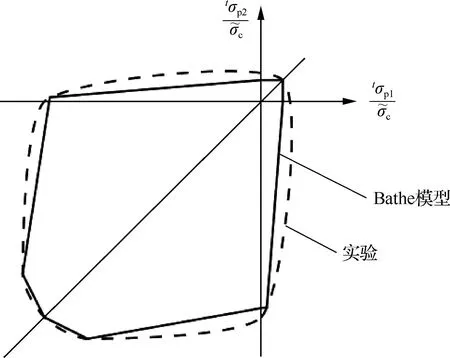
图1 双轴受压破坏包络线

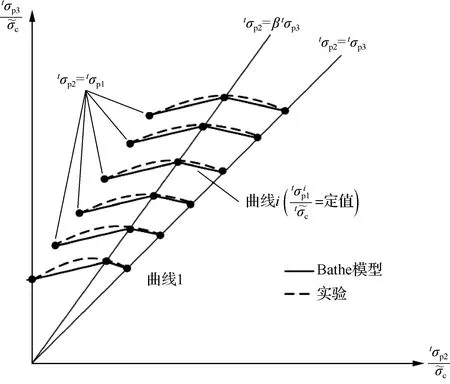
图2 三轴受压破坏包络线

1.2 D-P Cap本构模型

Drucker-Prager帽盖模型是基于D-P屈服准则、非关联的流动法则、理想塑性的D-P屈服行为、拉伸中止和帽盖硬化的本构模型。

该模型可用于处理常见的几何非线性问题。在用于小位移/小应变公式时，需要使用材料非线性方程。当用于大位移/小应变表达时，要使用TL方程；当用于大位移/大应变表达时，要使用UL方程。图3概述了Drucker-Prager模型的一些重要特性(包括拉伸中止和帽盖硬化)。

图3 子午面上的D-P Cap模型

Drucker-Prager屈服函数通过下式给出：

(1)

式中α，k——材料的特性参数，分别为内摩擦角φ和黏聚力c的函数；

tJ1——t时刻的应力第一不变量；

tJ2D——t时刻的偏应力第二不变量。

相应的势函数通过下式给出：

(2)

式中的β是剪胀角ψ的函数，u不需要作为输入参数。

参数α、β和k可以通过匹配Drucker-Prager准则和Mohr-Coulomb准则确定。

对于三轴压缩试验：

(3)

对于三轴拉伸试验：

(4)

对于平面应变试验：

(5)

帽盖屈服函数取决于帽盖的形状，对于平面帽盖：

(6)

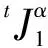
(7)

对于椭圆形帽盖：

tfc=(tJ1+tL)+R2(tJ2D-tB2)

(8)

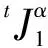
与von Mises模型不同，Drucker-Prager屈服准则不具有材料硬化性能(除了帽盖硬化以外，材料总是假定为理想弹塑性)。

2 工程案例

2.1 计算模型

以仁宗海堆石坝为例。最大坝高约56m，上游坝坡有一15m宽的坝体检修马道，马道以上坝体采用坝面复合土工膜防渗；马道以下坝体采用明浇混凝土防渗墙(下部与坝基防渗墙相接防渗)。坝基覆盖层采用混凝土防渗墙防渗，防渗墙位于坝轴线上游约84m处，最大深度为82m，墙厚1.0m。

为了保证计算精度，整体模型向坝体上下游各延伸300m，左右岸从坝肩各延伸200m，竖向取至2600m高程。坐标系选取：坝轴方向为X轴，正向指向右岸；河流方向为Y轴，正向指向下游；垂直方向为Z轴，正向垂直向上。模型底部采用全约束，模型坝轴向两侧采用X向约束，模型顺河向两侧采用Y向约束。整体模型采用8节点六面体等参单元，单元总数为38156个，节点总数为41990个。整体模型见图4、图5。

图4 三维有限元整体模型

图5 三维有限元整体网格

对防渗墙采用子模型法模拟。子模型包括防渗墙(见图6)、墙顶细料、混凝土护板、垫层、覆盖层和两岸基岩子模型，子模型单元总数2100个，节点数23715个。

图6 防渗墙子模型有限元网格

2.2 模型参数与工况

堆石料和覆盖层采用邓肯E-B本构模型模拟，防渗墙混凝土分别用线弹性、Bathe模型和D-P Cap模型模拟，用节理单元模拟防渗墙与顶部细料、墙体前后及墙与基础的接触关系。基岩采用线弹性模型。

堆石体与基础的邓肯E-B本构模型参数见表1，堆石体参数按实验值结合同类工程补充确定。河床覆盖层由于无试验数据，参考同类型工程取值。基岩及防渗墙材料参数见表2。

表1 土石料的邓肯E-B本构模型参数

表2 基岩及防渗墙材料参数

该堆石坝于2006年下半年开建，2008年8月完工。2008年10月11日开始水库蓄水。库水位于2009年1月2日升至2906.28m，为初次蓄水最高水位。为满足下游梯级电站枯水期的发电需要，该日后水库开闸放水，2009年3月20日，库水位降至2878.98m。2009年4月1日，水库进行第二阶段蓄水，2009年11月7日，水库蓄水至2930.00m高程，达到水库正常蓄水位[10]。

参考工程的实际填筑和蓄水状况，将加载过程分为17级，前8级模拟施工过程，9～17级模拟蓄水过程。具体方案见表3。

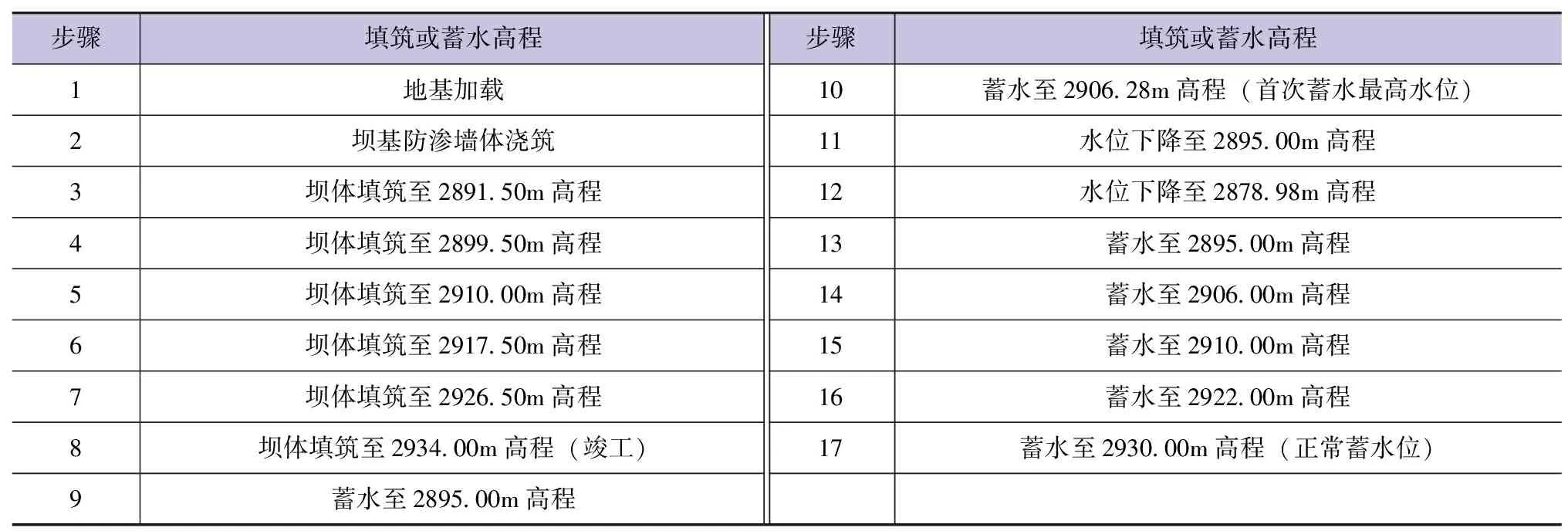
表3 填筑及蓄水过程模拟

2.3 防渗墙的开裂模拟

2.3.1 Bathe本构模型的开裂模拟

模拟的开裂结果见图7。裂缝的展示规定为：红色圆圈代表张开裂缝，蓝色圆圈代表闭合裂缝，红色星号代表压溃区域。本节裂缝开展过程图均按此标示。

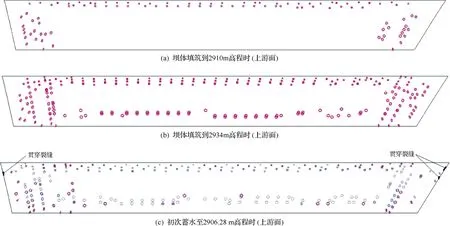
图7 防渗墙裂缝开展过程(Bathe模型)

a.施工期。经分析，在坝体填筑到2910m高程左右时，由于受到坝体的水平挤压作用，墙体向上游有较大的变形，产生较大的拉应力，墙体靠近两岸部位上游面和墙体上部上游面开始出现部分表面裂缝。其中，墙体上部主要为水平表面裂缝，墙体靠近两岸侧主要为横向表面裂缝，见图7(a)。随着坝体填筑高程的增加，裂缝数量和范围有所增加，截至竣工时，墙体底部亦出现少量纵向表面裂缝；此阶段，墙体下游面靠近两岸侧有极少数表面裂缝产生，见图7(b)。

b.初次蓄水。如图7(c)所示，开始蓄水后，墙体向上游的变形开始被压回，部分裂缝开始闭合，蓄水至2895m高程时，墙体上游面底部和两岸侧裂缝已经大部分闭合；当水位到达初次蓄水最高水位2906.28m时，墙体上游面上部裂缝大部分闭合，见图7(d)。此时，由于墙体的变形转向下游，墙体下游面底部出现部分纵向表面裂缝。同时，墙体与两岸连接处出现小范围的贯穿裂缝。

c.水位下降。水位下降后，墙体向下游的变形有所回弹，墙体上游面上部的部分闭合裂缝再次张开，下游表面裂缝变化不大，见图7(e)。

d.二次蓄水至正常蓄水位。水库开始二次蓄水时，裂缝的开展规律与初次蓄水相似，即随着水位的增长上游面的裂缝逐渐闭合，而下游侧的裂缝范围和数量有一定增加，主要集中在墙体底部附近，裂缝仍然以表面裂缝为主。图7(f)为正常蓄水位墙体上游面开裂示意图。

总的来说，在施工和蓄水过程中，混凝土防渗墙出现了部分表面裂缝和极少数贯穿裂缝，裂缝开展过程为：在施工期墙体上游面上部及靠近两岸侧先出现表面裂缝，随着坝体填筑高程的增加，上游面底部和下游面底部也出现少量裂缝。水库开始蓄水后，墙体上游面裂缝开始闭合，下游面底部裂缝范围有所增加；水位下降后，上游面已闭合的部分裂缝再次张开，下游面裂缝变化较小；二次蓄水至正常蓄水位时，上游面裂缝大部分已闭合，下游面底部和两岸侧出现一定的裂缝区域。

2.3.2 D-P Cap本构模型的开裂模拟

a.施工期。与Bathe模型模拟结果相同，防渗墙在坝体填筑至2910m高程时开始出现小范围裂缝，裂缝初始开裂情况见图8(a)。主要出现在墙体顶部和墙体靠近两岸侧，裂缝的范围随着坝体填筑高程的增加而增大，且裂缝主要为表面裂缝。图8(b)为竣工时的裂缝范围示意图。

图8 防渗墙裂缝开展过程(D-P Cap模型)

b.初次蓄水。初次蓄水之后，因为墙体的顺河向位移方向出现了改变，指向上游的位移被压回下游，因此，上游面的表面裂缝开始闭合，图8(c)为初蓄水至2895m高程时的墙体上游面裂缝示意图，可以看出裂缝范围已经较竣工期减小。蓄水至初次蓄水最高水位2906.28m时，裂缝范围已经相当小。同时墙体下游面底部出现了部分表面裂缝，见图8(d)。此时，墙体与两岸的连接处出现了局部的贯穿裂缝。

c.水位下降。水库开闸泄水后，随着水位下降，墙体的上游面上部再次出现表面裂缝，这是由于随着水压的减少，墙体指向下游的变形向上游反弹，蓄水后闭合的表面裂缝再次张开。图8(e)为水位下降至死水位时墙体上游面的裂缝示意图。同时，墙体下游面底部的表面裂缝变化并不明显。图8(f)为水位下降至死水位时墙体下游的裂缝示意图。

d.二次蓄水。二次蓄水后，墙体的变形继续继续向下游发展，而墙体上游面裂缝随着水位的增加而逐渐闭合，裂缝范围逐步减小。图8(g)为蓄水至正常蓄水位时的墙体上游面裂缝示意图。在水位上升的同时，墙体下游面底部的表面裂缝数量与范围有所增加，图8(h)为正常蓄水位时墙体下游面的裂缝示意图。同时墙体与右岸连接处的贯穿裂缝范围有小幅增加。

综上所述，采用D-P Cap本构模型模拟墙体开裂时，墙体在施工期的裂缝开展过程由坝体填筑到2910m高程开始，首先是墙体上游上部和两侧出现部分表面裂缝，裂缝的范围随着坝体的填筑高程增加而增大，墙体下游面也有小部分表面裂缝；初次蓄水后，上游面的裂缝大部分闭合，下游侧底部的裂缝范围有小幅增加，同时墙体两侧出现小范围贯穿裂缝；水库开闸泄水后，墙体上游面上部又出现部分裂缝，墙体下游面底部的裂缝范围有略微增大；水库二次蓄水后，墙体上游面的裂缝大部分闭合，墙体下游面底部和两侧有部分表面裂缝产生。其中，从初蓄水开始墙体两侧有少量的贯穿裂缝。

2.3.3 两种本构模型模拟开裂的对比

从前两节的分析可以看出，分别采用Bathe本构模型和D-P Cap本构模型模拟混凝土防渗墙的开裂的情况如下：

a.起裂位置和起裂时间基本一致。都是在坝体填筑到2910m高程左右时，墙体上游面顶部和靠近两岸侧出现表面裂缝。

b.裂缝开展过程也基本一致。即随着水库开始蓄水，墙体上游面的裂缝开始闭合，同时下游侧底部开始出现裂缝；水位下降后，防渗墙上游面再次出现裂缝，下游侧裂缝范围基本不变；二次蓄水后，防渗墙上游面裂缝基本完全闭合，下游侧底部和两岸侧出现一定范围的表面裂缝区。

c.贯穿裂缝位置大致相同。即墙体与两岸连接处的部分区域出现贯穿裂缝(主要为右岸)。

由以上三点可以看出采用两种本构模型模拟混凝土防渗墙开裂的结果基本一致，从一定程度上验证了模拟的合理性。

同时可以看出，采用弥散裂缝模型的Bathe本构模型计算出的裂缝范围要大于同等情况下D-P Cap本构模型的计算结果，这可能是由于弥散裂缝模型的网格依赖性引起的，即裂缝很容易沿着网格方向发展；另外，在某一荷载增量下，弥散裂缝模型可能会发生相邻多个单元的拉应力同时超过拉断应力，使本应只有一条裂缝的构件在有限元分析时会在部分相邻单元产生多条裂缝，造成与实际情况不符的情况。而D-P Cap模型则以片状屈服区表示裂缝。

从以上结果可以看出，防渗墙在坝体施工期会出现较多的裂缝，但是大多是表面裂缝，对防渗墙的安全和防渗不会有太大影响；而在运行期，特别是水位变化过程中，墙体与两岸连接处出现了小范围贯穿裂缝，这些贯穿裂缝会对坝基及坝肩的防渗造成较大影响。

3 与监测资料的对比分析

表4为二次蓄水期右岸量水堰所测得的渗流量成果，由表4可以看出，二次蓄水至2921.20m高程时，渗流量达到了206.06L/s；蓄水至正常蓄水位2930.00m时，渗流量为394.31L/s。正常蓄水位时的右岸实际渗流量远大于设计总渗流量73.72L/s[10]。同时，经现场检查发现，右岸设置的多个绕渗孔出现溢水。通过以上两方面的信息可以判定渗流情况为异常状态，由此可以推断造成较大渗流量的原因是有一定的集中渗流通道，而右岸侧坝基采用防渗墙防渗，防渗墙局部产生了贯穿裂缝可能是造成渗流异常的重要原因之一。而本节模拟计算的结果是防渗墙体与两岸连接处(主要集中在右岸，左岸极少)有一定范围的贯穿裂缝，这在一定程度上也佐证了本文开裂模拟结果的合理性。