粗糙铝表面光谱偏振BRDF的测量与建模

刘彦磊 刘子龙 周孝好

摘  要：金属铝在航空航天、军事国防、电子通信等领域具有重要应用，对铝材料表面光谱偏振散射特性的研究有助于丰富材料的光学信息，能够为铝材料的应用提供数据支撑.首先基于一套传统双向反射分布函数（bidirectional reflectance distribution function，BRDF）測量装置在近红外波段测量了粗糙铝表面的光谱偏振BRDF，并分析了入射天顶角、粗糙度等因素对测量结果的影响.测量结果表明：入射角、波长、偏振态和表面粗糙度对BRDF有显著影响.其次，分别采用Beckmann分布和指数分布概率密度分布函数建立了BRDF模型，并对实验结果进行了拟合.通过对比能够发现：对于同一样品和相同入射条件，不同的模型能够得到不同的拟合结果；对于不同粗糙度的样品采用不同的模型可能得到更好的拟合结果.

关键词：光谱偏振；铝；粗糙度；近红外；双向反射分布函数模型

中图分类号：O433      文献标志码：A文章编号：1000-2367（2024）03-0113-06

铝是一种重要的轻金属，因其优异的性能被广泛应用于航空航天、电气、汽车工业等领域［1-5］，对其表面光学散射特性的研究能够丰富其光学特性数据，为铝在相关领域的应用提供数据支撑.因此，近几十年来关于铝表面光学特性的研究从未间断.贾辉等［1］基于自主搭建的装置研究了入射角度、粗糙度和波长对铝漫反射板的影响.张磊等［2］测量了波长为1 064 nm时铝表面的双向反射分布函数（bidirectional reflectance distribution function，BRDF），研究了粗糙度和入射角度对测量结果的影响.帅永等［6］通过实验方法对微粗糙硬铝表面的散射特性进行了测量，结果表明：在长波及大角度入射时后向散射明显增强.孟令鹏等［7］在200～1 000 nm波长范围内收集了25～500 ℃铝板表面加热过程以及500～25 ℃冷却过程中材料表面的散射谱数据，指出温度变化对材料吸收率或反射率产生的影响是引起材料表面BRDF值变化的主要原因.

然而，已有的研究主要集中在非偏振BRDF的测量，关于偏振BRDF的研究很少见到报道.研究铝表面的偏振光谱BRDF能够提供更全面的光学散射信息［8］，在目标检测和识别中具有重要的应用价值.本文在近红外波段测量了铝的光谱偏振BRDF，分析了粗糙度、入射角和波长等因素对测量结果的影响，并基于不同的法线密度分布函数建立了BRDF模型.

1  测量装置及参数设置

采用传统的BRDF测量装置，主要包含光源、探测系统及转角装置，机械部分设计图和光路图及试验系

收稿日期：2023-09-11;修回日期：2023-11-10.

基金项目：红外物理国家重点实验室开放课题（SITP-NLIST-ZD-2023-06）.

作者简介：刘彦磊（1986-），男，河南郑州人，中国计量科学研究院讲师，博士，主要从事目标表面双向反射分布函数测量与应用方面的研究.

通信作者：刘子龙，E-mail：liuzl@nim.ac.cn.

引用本文：刘彦磊，刘子龙，周孝好.粗糙铝表面光谱偏振BRDF的测量与建模［J］.河南师范大学学报（自然科学版），2024，52（3）：113-118.（Liu Yanlei，Liu Zilong，Zhou Xiaohao.Measurement and modeling of spectral polarized BRDF of rough aluminum surface［J］.Journal of Henan Normal University（Natural Science Edition），2024，52（3）：113-118.DOI：10.16366/j.cnki.1000-2367.2023.09.11.0001.）

统的主要技术指标分别在附录图S1和表S1中给出.其中，光源选用具有很好准直性、均匀性和稳定性的溴钨灯（GLORIA-T250A），探测器选用与溴钨灯光源的光谱特性和电路特性相匹配的电制冷铟镓砷探测器（DInGaAs 2600-TE），高精度转角装置可以实现空间上的4个变量（θi，φi，θr，φr）的控制［9-10］.

本研究的测量原理［9-10］为ff（θi，φi，θr，φr，λ）=Lr（θi，φi，θr，φr，λ）Lo（0，0，0，0，λ）·1Ωrcos θi，（1）

其中，θi和φi表示入射天顶角和方位角，θr和φr表示反射天顶角和方位角，λ表示波长.Lr（θi，φi，θr，φr，λ）反射辐射亮度，Lo（0，0，0，0，λ）为反射镜的反射辐亮度，在测量时等效为光源辐射亮度，Ωr为探测立体角，cos θi为角度因子.

本实验测量的波长范围为1 200～2 400 nm，间隔为5 nm；入射天顶角的范围为5°～75°，间隔为5°.对于给定的入射角，反射天顶角的测量范围为-90°～90°，在镜面反射方向附近的角度间隔设定为1°，远离镜面反射方向的区域设定为2°.入射光为非偏振光，反射光分别为s偏振和p偏振光.需要指出的是，虽然在测量中反射天顶角的范围设置为-90°～90°，仅给出了测量结果大于零的部分.

2  样品制备

选择厚度为3 mm，直径为50 mm的圆形铝片作为样品.首先，用金属抛光机对样品进行抛光，然后选取粗糙度为120目、400目、800目和1 200目的SiC砂纸分别对4个样品进行打磨；然后，采用质量分数99.5%的丙酮溶液和无水乙醇清洗样品；最后，将样品放入纯净水中并使用超声波清洗机进行进一步清洗，以确保表面无污垢残留.加工完成后，将样品依次标记为1#、2#、3#、4#.并用粗糙度测试仪（TimeTR220）测量样品表面粗糙度，分别测得表面算术平均粗糙度Ra=0.465、0.165、0.135、0.089.采用光学显微镜（Motic BA310met）对样品的表面形貌进行了表征，如附录图S2所示.

3  结果与讨论

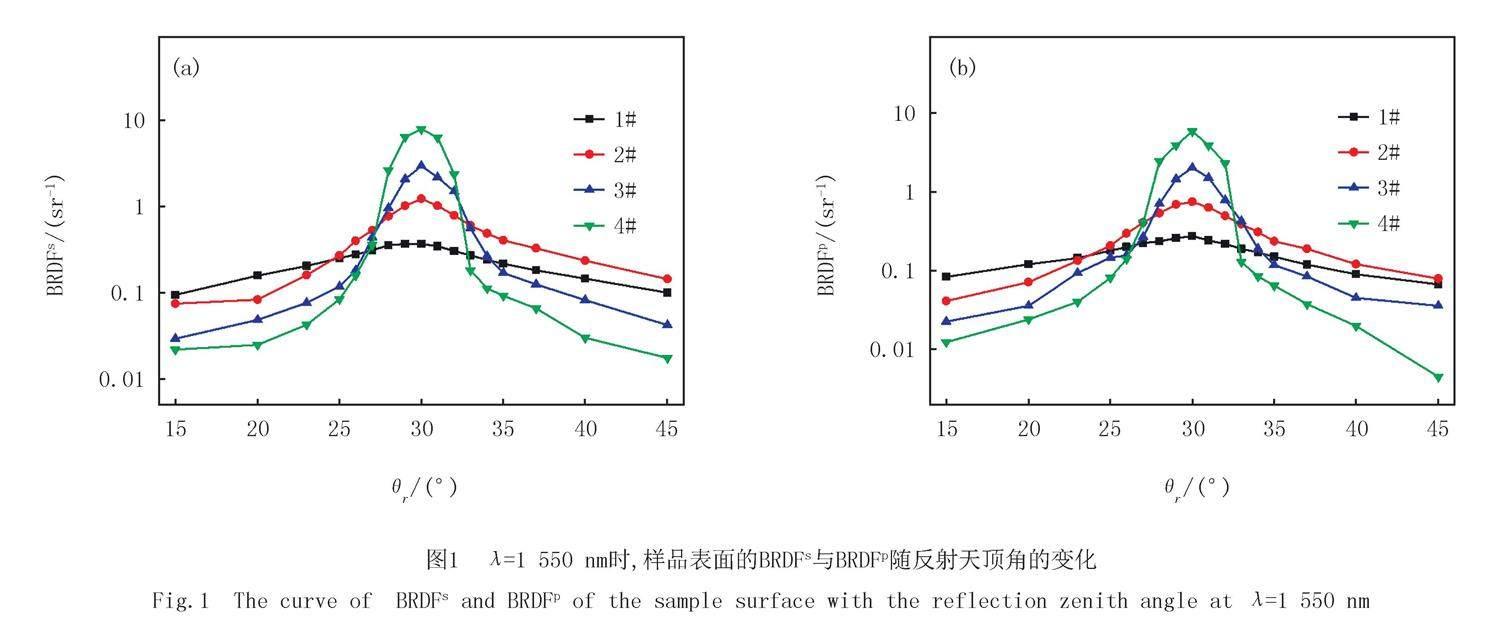
为了研究表面粗糙度对BRDF的影响，在θi=30°、λ=1 550 nm下测量了1#～4#样品的偏振BRDF并计算了BRDF的对数值，结果如图1所示，其中，BRDFs和BRDFp分别表示反射光为s偏振和p偏振时的BRDF值.显然，BRDF随着反射天顶角的增大而先增大后减小，峰值出现在θi=θr方向，且峰值随样品表面粗糙度的减小而增大.观察图1可以看出，随着粗糙度增加，偏离峰值位置的BRDF逐渐增大.这说明样品表面的粗糙度对BRDF具有明显的影响.此外，能够发现反射光的偏振态对BRDF随反射天顶角的变化趋势没有影响.

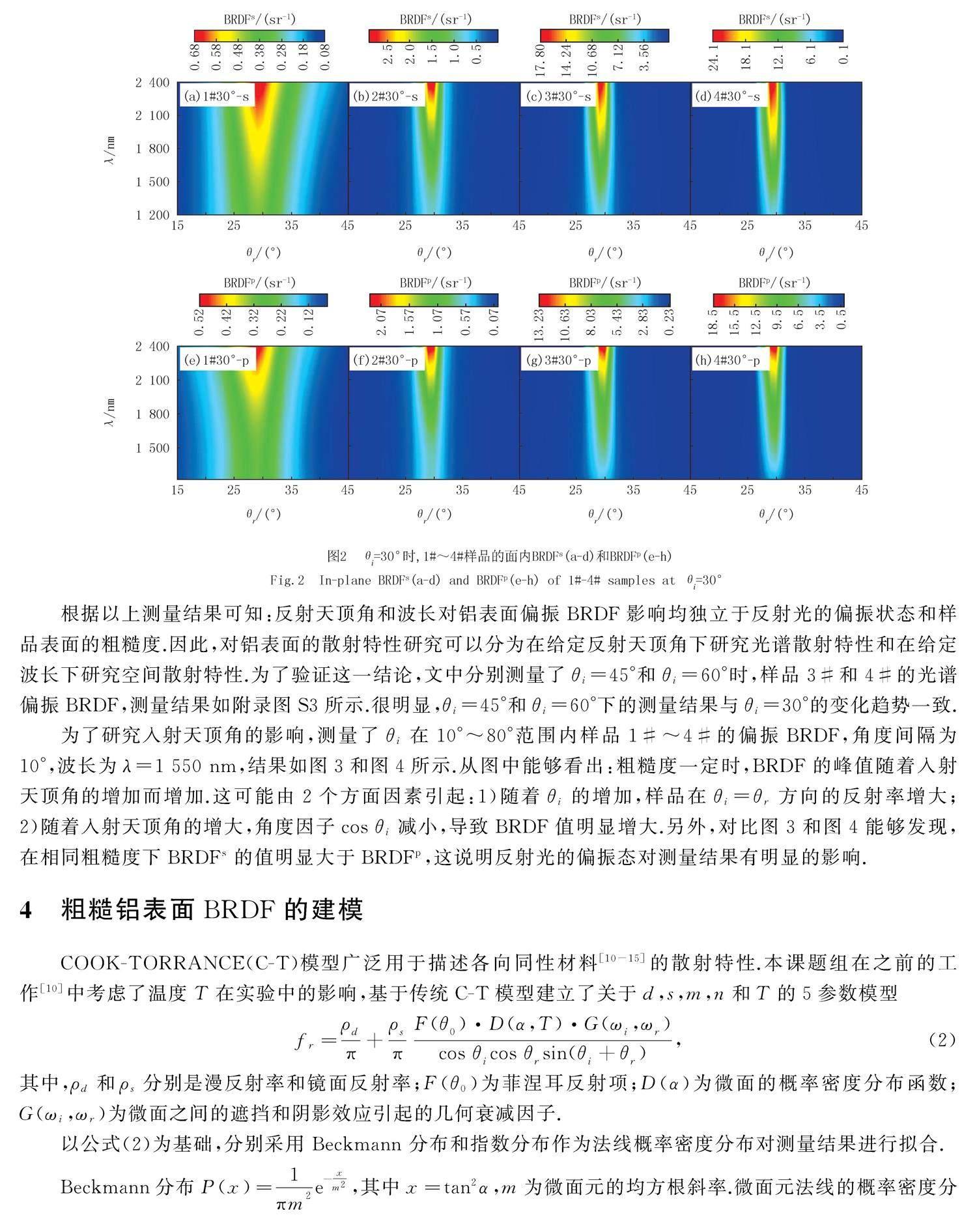
为了分析波长和反射天顶角对粗糙铝表面偏振BRDF的影响，文中对θi=30°时样品1#～4#的光谱偏振BRDF进行了测量，结果如图2所示.从图2（a）可以看出，在波长一定时，BRDFs随着θi的增加先增大后减小，峰值出现在θi=θr方向；入射天顶角一定时，随着波长增加，BRDFs在镜面方向附近逐渐增大，在偏离镜面方向几乎不发生变化.通过图2（a-d）可以看出，粗糙度对铝表面BRDF随反射天顶角和波长的变化趋势几乎没有影响.对比图2（a-d）和图2（e-h）可以看出BRDFp的变化趋势与BRDFs一致，这说明反射光的偏振状态对样品BRDF的变化趋势没有影响.

根据以上测量结果可知：反射天顶角和波长对铝表面偏振BRDF影响均独立于反射光的偏振状态和样品表面的粗糙度.因此，对铝表面的散射特性研究可以分为在给定反射天顶角下研究光谱散射特性和在给定波长下研究空间散射特性.为了验证这一结论，文中分别测量了θi=45°和θi=60°时，样品3#和4#的光谱偏振BRDF，测量结果如附录图S3所示.很明显，θi=45°和θi=60°下的测量结果与θi=30°的变化趋势一致.

为了研究入射天顶角的影响，测量了θi在10°～80°范围内样品1#～4#的偏振BRDF，角度间隔为10°，波长为λ=1 550 nm，结果如图3和图4所示.从图中能够看出：粗糙度一定时，BRDF的峰值随着入射天顶角的增加而增加.这可能由2个方面因素引起：1）随着θi的增加，样品在θi=θr方向的反射率增大；2）随着入射天顶角的增大，角度因子cos θi减小，导致BRDF值明显增大.另外，对比图3和图4能够发现，在相同粗糙度下BRDFs的值明显大于BRDFp，这说明反射光的偏振态对测量结果有明显的影响.

4  粗糙鋁表面BRDF的建模

COOK-TORRANCE（C-T）模型广泛用于描述各向同性材料［10-15］的散射特性.本课题组在之前的工作［10］中考虑了温度T在实验中的影响，基于传统C-T模型建立了关于d，s，m，n和T的5参数模型fr=ρdπ+ρsπF（θ0）·D（α，T）·G（ωi，ωr）cos θicos θrsin（θi+θr），（2）

其中，ρd和ρs分别是漫反射率和镜面反射率;F（θ0）为菲涅耳反射项；D（α）为微面的概率密度分布函数；G（ωi，ωr）为微面之间的遮挡和阴影效应引起的几何衰减因子.

以公式（2）为基础，分别采用 Beckmann 分布和指数分布作为法线概率密度分布对测量结果进行拟合.

Beckmann分布P（x）=1πm2e-xm2，其中x=tan2α，m为微面元的均方根斜率.微面元法线的概率密度分布函数项D（α）=χ［0，π/2］（α）cos4αP（x），其中χ［0，π/2］（α）=1，［0，π/2］，0，其他.

指数分布Pe（x）=（1-x）24π（4x+m2）（1+x）2，其中，x=tan2α，α=sin θsin φ，m为微面元均方根斜率.因此，指数型微面元发现的概率密度分布函数项De（α）=χ［0，π/2］（α）cos4αPe（x）=χ［0，π/2］（α）cπ（4tan2α+m2），其中c为大于0的常数.

残差平方和（SSE）是用来衡量模型拟合程度的量，一组数据的残差平方和越小，其拟合效果越好.Beckmann 分布和指数分布的拟合结果如图5所示.通过对比曲线的吻合情况及SSE值可以看出 ，对于 1#和2#样品，指数分布的SSE小于Beckmann 分布的SSE，说明指数分布的拟合值与测量值符合较好；对于3#和4#样品 ，Beckmann的拟合值与测量值符合较好.这说明，当样品表面较为粗糙时，指数分布能够较好表征表面的微面元法线分布；当表面较光滑时Beckmann分布能够较好的表征表面的微面元法线分布.拟合结果说明：对于同一样品的测量数据，采用不同的模型或者法线密度分布函数能够得到不同的拟合结果；即使对于同一种材料，也很难通过单一模型准确获得其表面的光学散射特性.这对BRDF模型的普适性提出新的要求.

基于以上结论，分别采用指数分布和Beckmann分布对1#～4#样品的BRDF进行拟合.BRDFs和BRDFp的测量结果和拟合结果在附录图S4中给出.从图S4中能够看出，采用不同微面元法线分布组合的方式建立模型对测量结果进行拟合能够得到更好的结果.

5  结  论

本文基于一套传统BRDF测量装置在近红外波段对不同粗糙度的铝表面进行BRDF测量，详细分析了粗糙度、入射角度、波长等因素对铝光谱偏振BRDF的影响.测量结果表明，以上几个因素对偏振光谱BRDF有明显的影响.此外，分别采用Beckmann和指数2种微面元法线概率密度分布函数，基于4参量基本模型结构建立了BRDF模型，并对实验结果进行了拟合.对比拟合和测量结果能够发现：1）对于同一样品，不同的模型能够得到不同的拟合结果；2）对于不同粗糙度的样品采用不同的模型可能得到更好的拟合结果.本文的研究工作一方面为铝光学特性研究和应用提供了数据支撑，另一方面为建立BRDF模型提出了新思路——多模型组合.

附录见电子版（DOI：10.16366/j.cnki.1000-2367.2023.09.11.0001）.

参  考  文  献

［1］   贾辉，李福田.铝漫反射板200～300 nm相对双向反射分布函数的实验研究［J］.光学学报，2004，24（2）：230-234.

［2］张磊，杨鹏翎，赵海川，等.铜铝材料粗糙表面的BRDF特性研究［J］.现代应用物理，2018，9（4）：65-69.

ZHANG L，YANG P L，ZHAO H C，et al.Characteristics of bidirectional reflectance distribution function on roughness surface of copper and aluminum materials［J］.Modern Applied Physics，2018，9（4）：65-69.

［3］杨玉峰，吴振森，曹运华.合金铝表面近红外波段光学常数的反演与双向反射分布函数的计算［J］.光学学报，2011，31（2）：0229001.

［4］谢鸣，黄勇，王晓春，等.建筑材料表面红外双向反射分布函数实验分析［J］.哈尔滨工业大学学报，2011，43（3）：49-53.

［5］NICODEMUS F E.Directional reflectance and emissivity of an opaque surface［J］.Applied Optics，1965，4（7）：767-775.

［6］帥永，刘彬，杨果，等.微粗糙硬铝表面双向反射特性实验研究［J］.工程热物理学报，2010，31（4）：671-674.

［7］孟令鹏，李龙，陆旭，等.温度变化对铝材料的BRDF影响研究［J］.通讯世界，2016（6）：246.

［8］LAI Q Z，XIE Y M，GUO P，et al.Multi-spectral bidirectional reflectance characteristics of crude oils［J］.Infrared Physics & Technology，2020，109：103420.

［9］LIU Y L，YU K，LIU Z L，et al.Polarized BRDF measurement of steel E235B in the near-infrared region：based on a self-designed instrument with absolute measuring method［J］.Infrared Physics & Technology，2018，91：78-84.

［10］CHEN Z Y，LIU Y L，LIU J Y，et al.The measurement and modeling investigation on the BRDF of brass under variable temperature［J］.Infrared Physics & Technology，2023，128：104505.

［11］WESTIN S H，ARVO J R，TORRANCE K E.Predicting reflectance functions from complex surfaces［J］.ACM SIGGRAPH Computer Graphics，1992，26（2）：255-264.

［12］TOMINAGA S，NISHI S.Surface reflection properties of oil paints under various conditions［C］//Proc SPIE 6807，Color Imaging XIII：Processing，Hardcopy，and Applications，2008，6807：186-193.

［13］YU C，SEO Y，LEE S W.Global optimization for estimating a multiple-lobe analytical BRDF［J］.Computer Vision and Image Understanding，2011，115（12）：1679-1688.

［14］LI M Z，ZHAO J G，ZHOU Y T.Analysis of the modification method for cook-torrance model［J］.Applied Mechanics and Materials，2014，556/557/558/559/560/561/562：4240-4243.

［15］COOK R L，TORRANCE K E.A reflectance model for computer graphics［J］.ACM Transactions on Graphics，1（1）：7-24.

Measurement and modeling of spectral polarized BRDF of rough aluminum surface

Liu Yanlei1， Liu Zilong1， Zhou Xiaohao2

（1. Center for Metrology Scientific Data and Energy Metrology， National Institute of Metrology， Beijing 100029， China;

2. Shanghai Institute of Technical Physics; State Key Laboratory of Infrared Physics， Chinese Academy of Sciences， Shanghai 200083， China）

Abstract： Aluminum plays a vital role in aerospace， military defense， electronic communication， and other fields. Investigating the spectral polarization scattering characteristics of aluminum materials enriches the understanding of their optical properties and aids in providing data support for their applications. In this paper， the spectral polarization BRDF（bidirectional reflectance distribution function） of rough aluminum surface is measured in near infrared band based on a set of traditional BRDF measuring device， and the effects of incident zenith angle and roughness on the measurement results are analyzed. The results shows that the incidence angle， wavelength， polarization state and surface roughness have significant effects on BRDF. Additionally， the BRDF model is established by employing the Beckmann and exponential probability density functions， which are used to fit the experimental results. By compared with different models， it can be found that different models can get different fitting results for the same sample and incident condition. Better fitting results may be obtained by using different models for samples with different roughness.

Keywords： spectral-polarized; aluminum; roughness; near-infrared; BRDF model

［責任编校  杨浦  刘洋］

附  录