GeoGebra辅助下螺旋运动模型可视化分析
2024-05-15温文玉宋善炎
温文玉?宋善炎

以螺旋运动为背景的问题在高中物理中较为典型,在习题中尤为常见。这类问题常以不等距螺旋线运动和等距螺旋线运动两种类型出现。带电粒子在磁场中的运动是高中物理磁场教学的重点与难点之一。对带电粒子在有界磁场中运动问题的探析可细分为探讨动态问题、分析临界问题和求解多解问题。在磁场中,若带电粒子射入匀强磁场内的速度方向与磁场方向平行,则带电粒子不受洛伦兹力;带电粒子射入匀强磁场内的速度方向与磁场方向垂直,带电粒子受洛伦兹力,若带电粒子仅受洛伦兹力,则做匀速圆周运动;当带电粒子射入匀强磁场内的速度方向与磁场方向存在一定夹角,若仅受洛伦兹力,带电粒子做等距螺旋运动,当处于电场与磁场的叠加场中,带电粒子可做不等距螺旋运动。带电粒子在磁场中的运动轨迹复杂多变,学生难以理解和掌握,构建不同类型的复杂运动也存在困难。教师运用GeoGebra软件,能够直观形象地演示带电粒子的运动情况,清晰呈现动态化的运动过程,化抽象为形象,帮助学生构建物理模型,提高想象和思维能力。
一、GeoGebra软件在物理教学中的应用
目前,在物理教学中,GeoGebra软件主要应用于物理概念教学、习题教学、实验教学和辅助教学探究等方面[1]。在物理教学中会遇到许多抽象的物理模型,如果仅靠教师依据教材或题目等静态资料进行讲解,学生难以理解,应用GeoGebra等交互软件能够对物理过程进行有效动态模拟[2]。教师借助GeoGebra将数字符号转化为图像表征,有利于学生构建知识体系,提高思维能力[3]。GeoGebra在物理教学中的深度融合涉及很多物理知识的教学与研究,包含动态平衡、磁场、电场、光的干涉、匀速圆周运动、波函数叠加与简谐振动、追及与相遇等。
二、問题情境
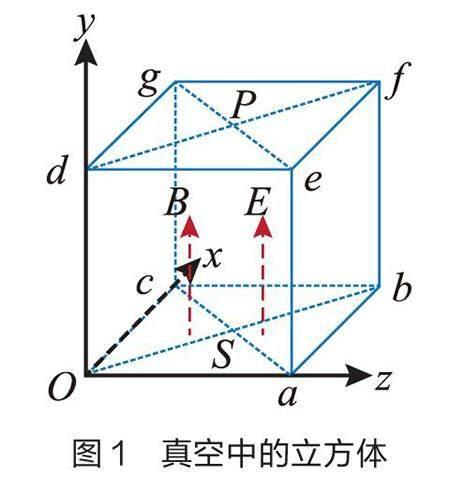
如图1所示,真空中的立方体边长为0.4 m,底面中心有一能向水平各个方向均匀发射α粒子的点状放射源(不考虑其他方向产生的α粒子),所有α粒子的速度都是v=3.0×106m/s,已知α粒子电荷量与质量之比 =5.0×107C/kg,立方体内有竖直向上的匀强电场和匀强磁场。abfe面放有一个屏,该屏可以沿z轴左右平移。
(1)要使所有粒子均能从上表面离开,匀强磁场最小值B1为多少?
(2)调整匀强磁场的大小,当匀强磁场B2=1 T时,要使所有粒子刚好都能从上表面中心P离开,所加匀强电场的最大值和离开P点时速度方向与defg水平面的夹角分别是多少?
(3)保持匀强磁场B2=1 T,匀强电场为第(2)问中的最大值,现让abfe屏沿z轴负方向移动0.11 m,求abfe屏上射出粒子x坐标取得最大值和最小值时对应点的y轴坐标。
三、GeoGebra建模助力学生想象与思考
此题考查的知识点是带电粒子在磁场中做不等距螺旋运动。带电粒子在磁场中做不等距螺旋运动,一般可分解为垂直于磁场方向平面内的匀速圆周运动和沿磁场方向的匀加速直线运动[4]。
(一)借助软件求解磁场临界问题
要使所有粒子均从上表面离开是一个研究磁感应强度取值的问题。由于带电粒子速度不同,磁感应强度不定,带电粒子在有界磁场中的运动轨迹发生变化。这类问题的特点在于,带电粒子受磁场边界的约束会出现“恰好”不穿出磁场区域的临界情形。学生解答这类问题,需要探究带电粒子恰好不穿出磁场区域的临界条件,画出带电粒子轨迹图。为了了解条件改变对粒子轨迹的影响,教师应用GeoGebra软件进行直观演示,让学生学习基本操作。软件作图标准且美观,更利于学生展开探究活动。
粒子在电磁场中的运动是水平面的匀速圆周运动与竖直方向(y方向)的匀加速直线运动的合成。学生经过问题(1)“要使所有粒子均从上表面离开”的分析可知,粒子在磁场力作用下圆周运动半径最大值为Rm= 。qvB1=m,代入数据可得B1=0.6 T,即要使所有粒子均从上表面离开,匀强磁场最小值为0.6 T。
下面,借助GeoGebra软件精确绘制带电粒子的运动轨迹。
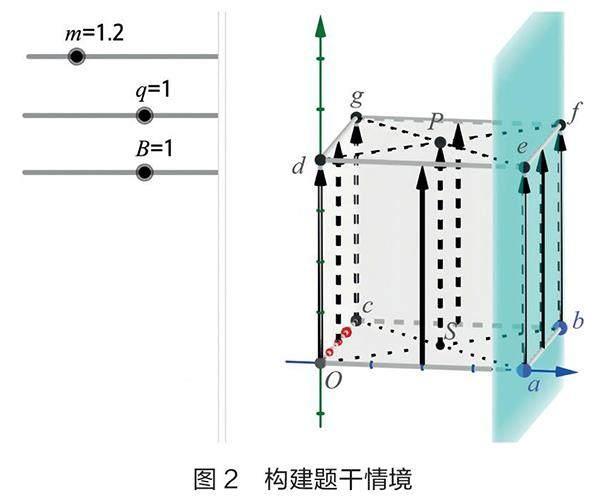
第一步:构建题干情境。
设置m、q、B滑动条,在3D视图工具栏中选择正六面体工具绘制磁场所在区域:边长0.4 m的正六面体a1,在工具栏中选用平面工具绘制与abfe面相交的屏。分别作出Oabc、defg两个平面的对角线,将Oabc、defg平面对角线的交点分别设置为S、P。设置磁场空间序列B=序列(序列(向量((i,0,z),(i,0.4,z)),i,0,0.4,(( 0.2 )/(B))),z,0,0.4,(( 0.2 )/(B))),如图2所示。
第二步:绘制带电粒子在磁场中的运动轨迹。
设置t、vox滑动条,voz= (9-vox2),带电粒
子入射磁场的初速度v0=向量(S, (x(S)+vox,y(S),z(S)+voz))。设置α=angle (v0)为初速度v0与x轴夹角,半径r= 。描点C({x(S)-rsin (α+90°),y(S),z(S)-rcos (α+90°)})。作出带电粒子在磁场Oabc平面以C为圆心,r为半径的轨迹 (如图3)。
如何利用绘制的粒子轨迹寻找所有粒子均能从上表面离开时磁感应强度的最小值?学生拖动滑动条B改变磁感应强度,观察可知,当匀强磁场小于0.6 T时,部分粒子未到达上表面已射出磁场;当匀强磁场大于0.6 T时,粒子均从上表面离开。对于带电粒子均能从上表面离开的运动分析,涉及的知识包含洛伦兹力、匀速圆周运动。学生抓住临界条件并寻找几何关系,进行定性分析与定量计算可求出匀强磁场最小值。该问题难度不大,用于测评学生获取信息能力、推理能力和运算能力。为有效探究磁感应强度对粒子运动轨迹的影响,并可视化分析其他因素对粒子运动轨迹的影响,教师让学生对影响粒子运动轨迹的条件进行理论推导后再应用软件操作,使其感受动态软件模拟的直观便捷,体会条件改变对带电粒子运动轨迹的影响。
(二) 求解匀强电场最大值和有关夹角
当带电粒子在磁场条件的限制下均能从立方体上表面离开,又如何利用电场限制带电粒子从立方体上表面的中心离开磁场?这是一个复合场的问题。学生面对带电粒子在复合场中的运动问题,往往有畏难情绪。对于带电粒子在复合场中的运动,学生需要作图辅助探究,其中对作图要求较高。在例题中,由前述可知,所有粒子均能从上表面离开,若粒子需从P点离开,则粒子的运动时间恰好为运动周期T的整数倍。此时,匀强电场的取值并不唯一,如何让所加匀强电场为最大值?结合牛顿运动定律作受力分析是常用的分析方法。分析可知,当粒子只运动一个周期离开P点时,所加匀强电场为最大。由题(1)可知,当匀强磁场B2=1 T时,所有粒子均只能从上表面离开,运动周期为T= 。当粒子只运动一个周期离开P点时,所加匀强电场为最大,即L=T2,代入數据得E= ×107 N/C。离开P点时y方向速度大小为vy= T,设离开P点时方向与defg水平面的夹角为θ,则有tanθ= ,代入数据得tanθ= 。
在第一问的基础上,继续绘制带电粒子在磁场中的运动轨迹。
第一步:绘制带电粒子在三维空间的运动轨迹。
设置E滑动条,ay=为带电粒子在y方向上的加速度。带电粒子在三维空间的轨迹S1为(x(C)+rcos (ωt+α),y(C)+1/2ayt2,z(C)-rsin(ωt+α)),如图4所示。
第二步:模拟带电粒子从上表面P点离开。
学生改变E滑动条,可以清楚地观察带电粒子从上表面离开的位置变化。学生发现要使粒子刚好都从上表面中心P离开,则带电粒子的轨迹恰好为运动一周期的整数倍。
第三步:绘制任意位置速度与xOz平面夹角。
设置任意位置速度v、沿xOz平面速度及沿y方向速度vy。任意位置速度与xOz平面夹角θ=angle (v,vx)。
观察θ变化则能够直观地感受带电粒子任意位置的速度与xOz平面夹角的变化。
由题意可知,当调整匀强磁场至B2=1 T,带电粒子运动轨迹的半径和周期不变。学生借助GeoGebra软件建模发现,当电场强度E逐渐增大时,到达defg表面所需时间逐渐变短,即粒子从defg表面离开所需的时间变短。问题(2)中任务的要求不仅要使粒子从defg表面离开,而且是从P点离开。学生借助GeoGebra软件建模发现,只有当带电粒子的运动时间恰好为带电粒子做圆周运动周期的整数倍时才能满足从P点离开的条件。对比发现,理论推理过程较为复杂,如参数变化,学生用作图的方式探究更为复杂的粒子运动,难度很大。学生应用GeoGebra软件,拖动滑动条即可进行探究,不仅作图效率高,而且更加精确。教师引导学生改变匀强电场进而改变粒子运动轨迹,直观展示螺旋运动模型。学生很快掌握螺旋运动特征,深入思考螺旋运动模型的应用,有利于提高发散性思维能力。
探讨带电粒子如何从defg表面P点离开,意在测评学生对与带电粒子在磁场与电场复合场中运动情况的分析,以及涉及带电粒子在三维空间的曲线运动。学生需要具备较强的空间想象能力。在解决该问题的过程中,学生需要运用电场力、洛伦兹力、匀速圆周运动、运动的合成与分解等物理概念和物理规律进行思考,建立与发展物理观念。教师引导学生控制变量及根据题干信息推理求解匀强电场的电场强度的最大值,旨在培养学生获取信息能力、推理能力、模型构建能力、证据意识,在解决问题的过程中提升学生的科学思维能力,提高学生物理学科核心素养。
(三)求解极值对应坐标
在匀强磁场与匀强电场取值均已确定,带电粒子在复合场中的运动轨迹的半径及周期不变的情况下,带电粒子可从不同角度入射至复合场,当abfe屏左移0.11 m后,是否所有粒子依然能从上表面离开?由于磁场边界发生变化,学生需要结合几何关系对从abfe屏上射出粒子x坐标的最大值和最小值求解。相关计算和绘图可借助GeoGebra软件完成。
由qvB2=m,R=0.06 m。P1为abfe屏上射出粒子x坐标最大值位置,M为过S点垂直于abfe屏的垂线与abfe屏的交点,由几何关系可得xmax= +P1M,由于SM=0.9 m,可得xmax= ( 20+
)×10-2m,对应的y方向坐标值为y1=
=0.1 m。abfe屏上射出粒子x坐标最小值位置,由几何关系可得xmin= -R= (0.2-0.03 ) m,对应的y方向坐标值为y2=
= m。
在问题(2)的基础上,教师借助软件模拟当abfe屏左移0.11 m后,在abfe屏射出粒子x坐標取得最大值和最小值时对应点的y轴坐标。学生在工具栏中选用平面工具,绘制左移0.11 m后的abfe屏,查看俯视图,找到带电粒子的运动轨迹与abfe屏的交点位置。改变vox滑动条可改变带电粒子的运动轨迹,观察找到在abfe屏上射出粒子x坐标取得最大值和最小值所在位置。
匀强磁场、匀强电场均保持不变,教师将abfe屏左移0.11 m,让学生分析x值最大和最小时的情况。学生要完成这一任务需要具备较强的想象能力,能够建立物理模型与几何图形的联系,数形结合解决物理问题。借助数形结合分析解决物理问题,有利于培养学生的模型建构能力并增强空间想象能力。
教师借助GeoGebra 软件绘制带电粒子在磁场中做螺旋运动的轨迹,将抽象问题形象化,增强了学生利用信息技术分析物理问题的主动性,激发学生以多种形式探索物理的勇气,拓展物理学习的宽度。教师利用可视化动态图引导学生动眼观察、动手体验、动脑猜想,让学生经历严谨的探究过程,使其养成了科学严谨的态度,学会深度思考。高中物理教师在教学过程中需要讲解许多抽象但又重要的知识。教师用GeoGebra等软件对相应模型进行直观动态的可视化展示,有利于培养学生应用科学技术解决实际问题的自主学习能力,让他们在构建物理模型和深入探究物理规律的过程中提升物理核心素养。
为丰富学生求解物理问题的手段和方式,教师可以将信息技术与课堂教学深度融合。教师常态化地借助信息技术辅助讲解教学重难点和关键点,为学生赋能,有利于培养学生的科学精神与创新能力。
参考文献
[1] 龚圣卿,林钦.GeoGebra软件在物理问题表征中的应用[J].物理通报,2022(5):143-147.
[2] 刘健智,程婷.GeoGebra软件在物理可视化教学中的应用[J].物理教师,2021(6):70-73.
[3] 黄北京,刘毓球.用GeoGebra辅助高中物理微元思想的教学[J].物理教师,2013(4):58-59.
[4] 徐华兵.带电粒子在磁场中做螺旋运动类试题分类剖析[J].物理教师,2022(11):90-92.
(作者温文玉系湖南师范大学研究生;宋善炎系湖南师范大学教授,博士生导师)
责任编辑:祝元志
