助企纾困补贴与常规财政货币政策组合的效果比较*——基于DSGE 模型的模拟分析

罗 琦

（天津师范大学经济学院，天津 300387）

一、引言

2020 年新冠疫情突发叠加国外动荡的政治经济局势，对我国经济造成了较大冲击，使得诸多市场主体面临较大经营压力以至生存压力，同时也使得我国就业形势变得更为复杂和严峻。在这样的背景下，我国政府陆续出台了稳经济一揽子政策及其接续政策措施，推动经济加快恢复。稳增长稳就业保民生，关键是要保市场主体，针对市场主体特别是中小微企业、个体工商户和部分行业经营主体实际困难，加大对企业纾困的政策支持力度。作为特殊背景下出台的应急调控措施，助企纾困补贴政策与常规财政、货币政策如何协调配合才能实现最佳效果，是值得研究的重大现实课题。具体来说，助企纾困补贴政策与各种常规政策组合对就业和产出的刺激效果如何？给企业发放的助企纾困补贴是否越多越好？经济基本面的调控效果在不同政策组合下是否存在显著差异？研究上述问题对各级政府进一步落实纾困政策以及细化和创新惠企举措、维护我国改革发展稳定的大局，都具有重要意义。

已有文献多从实证层面分析助企纾困补贴的实施效果，部分文献从定性角度来分析助企纾困补贴政策的实施效果，但从理论视角对政策影响机制进行深入分析的文献并不多见。为进一步拓展助企纾困补贴政策实施效果的研究深度，本文构建一个包含招聘摩擦和工资黏性的DSGE 模型，探究助企纾困补贴政策与三种常规政策（宽松货币政策、降低消费税和扩张性财政政策）的搭配组合对就业和产出的影响机制，并对不同搭配组合的政策效果进行比较分析，以期为政府有关部门找准宏观政策取向一致性评估的发力点、更精准运用助企纾困补贴政策与各种货币、财税政策组合来调控就业和产出、推动我国经济回升向好、持续健康增长提供理论借鉴。

二、文献综述

迄今为止，学者们对助企纾困政策实施效果的研究大多从实证分析视角展开。王嘉琛（2021）通过使用模糊综合评价法对调查问卷结果加以分析，发现金融机构执行政策的积极性偏低、政策制定与中小企业需求存在结构性差异，是制约助企纾困金融政策发挥最佳作用的主要原因。毛捷和管星华（2021）运用双重差分模型实证分析地方政府助企纾困政策对上市公司业绩的影响，结果表明政策效果会因上市公司是否与融资平台公司存在关联交易表现出明显差异，纾困政策显著提高了与融资平台公司存在关联交易的上市公司的业绩。马征程和潘佳佳（2023）采用双重差分模型和三重差分模型实证研究疫情冲击下财政货币政策的助企纾困政策效应，发现疫情冲击下财政货币政策的助企纾困效应明显，有效帮助小微企业降低了信贷成本，提高了营业利润；研究同时发现，财政货币政策的助企纾困效应受到企业规模、地域分布等异质性因素的影响。

也有一些文献从调查分析以及定性分析层面讨论助企纾困政策的实施效果。李炜烨（2021）基于安徽省名录库随机抽样电话跟踪调查数据，跟踪了解样本企业的生产经营情况，结果表明安徽中小微企业生产经营信心持续增强，助企纾困政策效果显现，减税降费的作用最大。万相昱等（2021）基于企业汇算清缴大数据，并综合集成相关部门调查数据和发布信息，测算了2020 年国家推出的助企纾困政策对于小微企业抗击疫情的支持效果，并重点分析了一些重要的减税降费措施对小微企业的直接影响，以及对维持小微企业经营、稳定就业市场的综合效益。朱武祥等（2020）基于两次问卷调查的调研结果表明，助企纾困政策短期落地效果与企业期待有比较大的偏差，税费减免、信贷优惠的惠及面以及现金流缓解程度偏低。黄一松等（2021）研究发现民营上市公司出现股权质押风险时，有银行借款和银行借款越多的企业，其获取政府纾困的概率和支持力度越大。潘锡泉和郑亚莉（2022）对中小微企业融资在 “政策、信息、资金、渠道、服务”等维度上仍然不够畅通的现象进行剖析，并围绕这五个维度提出了深化融资畅通工程来纾困中小微民营企业的政策路径。

三、模型构建

本文构建的DSGE 模型包括经济活动中的四个主体部门：家庭部门、中间产品生产企业、最终产品生产企业和政府部门。为了更好地分析不同政策组合对就业的影响，模型中加入招聘摩擦和工资黏性等劳动力市场特征，主要是为了更好地模拟现实经济环境下助企纾困政策组合与劳动力市场之间复杂的交互作用机制，提高模型模拟结果的可信度。将产品生产商细分为中间产品生产商和最终产品生产商。中间产品生产商利用实物资本和家庭部门提供的劳动作为投入，生产中间品，在出售中间品后，付给家庭工资，这是因为DSGE 文献一般假设产商最终由家庭所有，中间产品生产商的剩余利润最终返还给家庭，最终产品部门把中间产品生产商生产的产品经加成定价后销售。政府的收入来自于政府部门发行的国债、政府向家庭征收的消费税和从家庭征收的一次性总付税，政府支出为购买性政府支出、向家庭的转移支付和国债利息支付，中央银行则在经济体系中对利率进行调控。理论模型中引入助企纾困政策的现实基础来源于2022 年5 月国务院印发的《扎实稳住经济的一揽子政策措施》。

（一）家庭

参考Faccini 和Yashiv（2022）的模型设置，假定代表性家庭通过选择消费和劳动实现跨期贴现效用最大化：

其中：φ>0、χ>0 分别为劳动供给弹性及劳动厌恶参数，家庭面临的预算约束为：

其中：Pt、Ct、It、Kt、Wt、Bt、Rt、Ⅱt、tret和Tt分别表示一般价格水平、家庭的实际消费、家庭的实际投资、家庭所拥有的实物资本、名义工资率、家庭购买的政府债券、无风险利率、企业给家庭的利润分红、政府向家庭的转移支付与政府向家庭征收的一次性总付税，τC t表示政府向家庭征收的消费税。设定τC t刻画政府征收的消费税冲击，该冲击的对数形式服从AR（1）过程：

其中：ρτ为消费税冲击的持续性系数，ρτ为消费税冲击的标准差，且ετ,t～N（0,1）。家庭实物资本的累计方程是：

其中：δK为资本折旧率。记t期初全社会失业工人总人数为，用Ht表示当期新招聘就业的总人数。记整个t期内社会上仍然失业的工人总数为Ut，则，从而t期总就业量的演化方程为Nt=（1-δN）Nt-1+Ht，其中δN为工人离职率。由于假设家庭为一测度为1的连续统，因而每一期期末失业人数和就业人数之和也为1，即Ut+Nt=1。求解关于Ct+s，Kt+s，Nt+s的消费者最优化问题的一阶条件可得：

（二）最终产品生产企业

最终产品生产企业投入中间品生产完全同质的最终产品Yt，其生产函数为：

其中：i∈（0,1）代表不同的中间产品生产企业，λp为中间产品之间的替代弹性。最终产品生产企业选择中间产品Yt,i，在生产函数（8）的约束下最大化利润。最终产品生产企业的最优化问题可以表示为：

解上述方程即可得到中间产品需求函数

其中：Pt,i是中间产品的价格，Pt是最终产品价格。由于最终产品市场是完全竞争的，均衡时最终产品生产企业的利润为0，这样总价格水平就可以表示为：

（三）中间产品生产企业

每个中间产品生产企业利用下面的生产函数生产和销售产品：

其中：ρA为技术冲击的持续性系数，ρA为技术冲击的标准差，且εA,t～N（0,1）。表示由于中间产品生产企业的招聘行为所导致的产出损失份额。参考Faccini 和Yashiv（2022），将招聘成本建模为一种产出成本，的函数表达式设定为，这种函数形式符合Furlanetto 和Groshenny （2016）学者利用实际微观数据对招聘成本的研究成果。假设企业招聘成本为企业招聘率的二次函数，其中企业招聘率定义为中间品生产企业i新招聘工人数Ht,i与企业i总招聘工人数Nt,i的比值，即Ht,i/Nt,i，全社会总就业人数即为每一个中间品生产企业i总招聘工人数Nt,i的加总。中的e>0 为一个标量参数，其含义代表中间产品生产企业的招聘摩擦系数。模型中之所以要对招聘摩擦等劳动力市场特征进行细节刻画，主要是为了更好地模拟现实经济环境下助企纾困政策组合与劳动力市场之间复杂的交互作用机制，从而提高模型模拟结果的可信度。

最后，中间品生产企业的最大化问题可表示为：

其中：Ψt和分别是约束（16）和（18）对应的拉格朗日乘子，并且ψt即为中间品生产企业的名义边际成本ψt=MCt，，，，。式（19）即为中间品生产企业面临的新凯恩斯菲利普斯曲线。式（20）表明了在引入招聘摩擦和政府的助企纾困型财政政策之后，中间品生产企业对劳动力的需求出现了明显的改变，实际工资不再只是等于劳动力的边际产品价值，而是会受到企业招聘成本和政府的助企纾困型财政政策的影响。通过求一阶导数可得，，说明招聘摩擦的存在会增加中间品生产企业的劳动力需求成本，而政府实施助企纾困型财政政策的力度会降低劳动力工资成本，从而使得企业愿意通过增加就业岗位来提高企业的利润。式（20）代表中间品生产企业对资本的需求函数。

（四）工资设定方程

由于假设劳动力市场存在招聘摩擦，工人的工资是通过纳什讨价还价（Nash Bargaining）模型来确定的。按照纳什讨价还价模型，工人的工资为下述最大化问题的解：

其中：ω定了实际工资黏性的大小程度，取值越大代表实际工资黏性越强。

（五）政府部门

政府部门的预算约束为：

财政收入政府发行国债Bt，向家庭征收消费税PtτC t Ct，从家庭征收一次性总付税Tt；财政支出包括政府向家庭的转移支付tret，政府公共支出Gt，国债利息支付Rt-1Bt-1。设定政府公共支出冲击的对数形式服从以下过程：

其中：ρG为公共支出冲击的持续性系数，σG为公共支出冲击的标准差，且εG,t～N(0,1)。假设中央银行采用盯住利率目标的货币政策，遵循满足修订的泰勒规则：

其中：Rt为无风险名义利率，为无风险名义利率的稳态值，ρ∈[0,1)表示利率平滑系数，φy≥0 和φπ≥1 表示利率对产出缺口与通胀缺口的反应强度。设定货币政策冲击Mt的对数形式服从以下过程：

其中：ρM为货币政策冲击的持续性系数，σM为货币政策冲击的标准差，且εM,t～N(0,1)。

（六）市场出清

产品市场和劳动力市场出清条件为：

σm为水平杆件对立杆产生的附加应力，取55N/mm2；KA为立杆截面调整系数（立杆为单杆时，KA取0.85）；KH为脚手架高度调整系数（当H≦25m时，KH取 0.8；当H＞25m时，KH取 0.99）；f为钢管抗压强度设计值，查规范可知取205N/mm2。

四、参数校准与贝叶斯估计

（一）参数校准

对于家庭部门的主观贴现因子的校准，根据模型稳态值的计算得β=1/R，通过计算近5 年银行间同业拆借利率的算术平均值得季度β校准值为0.99。参照仝冰（2010）将劳动负效用曲率设定χ为1，参照Faccini 和Yashiv（2022）将劳动供给弹性φ设为4。参照许伟和陈斌开（2009）将资本产出弹性设为0.61。对于资本折旧率δ的校准，参照黄赜琳（2005）采用年度10%折旧率，季度折旧率取值为0.024。参照Faccini 和Yashiv（2022）设定Rotemberg黏性价格程度为120。参照Faccini 和Yashiv（2022）将中间品替代弹性λp设置为11。以上各参数校准结果呈现在表1 中。

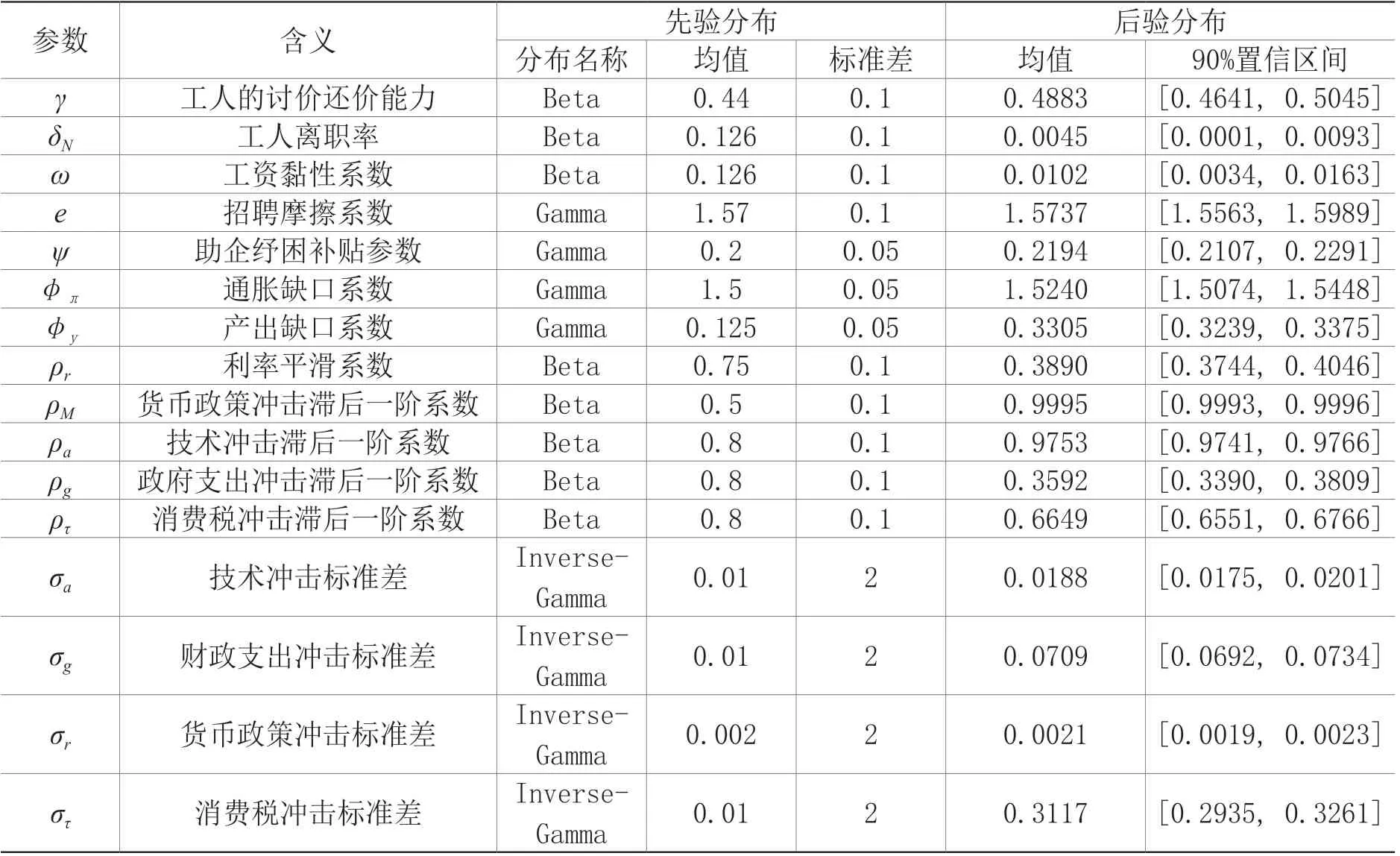
表1 参数贝叶斯估计结果

（二）参数的贝叶斯估计

除了上述参数外，对剩下的参数进行贝叶斯估计。贝叶斯估计中选取季度GDP、居民实际消费总额、投资总额、政府财政支出和通货膨胀率作为实际观测变量值，样本区间为1992年第一季度至2020 年第四季度，数据来源于Wind 数据库，上述数据再经由价格缩减调算、季节调整、HP 滤波处理后即为最终所得的数据。贝叶斯估计中先验分布中的超参数设置依据肖争艳和彭博（2011）和Liu 等（2013），取后验分布的马尔可夫蒙特卡洛（MCMC）抽样样本均值作为最终的参数贝叶斯估计值，结果见表1。

五、数值模拟与分析

（一）“助企纾困补贴+扩张性财政政策” 组合的实施效果

考察助企纾困补贴参数ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到扩张性财政政策冲击时所产生的脉冲响应，具体结果见图1 和图2。图1 中X 轴代表参数ψ取值，Y 轴代表ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到扩张性财政政策冲击时所产生的脉冲响应期数， Z 轴代表上述待考察宏观经济变量的稳态偏离值。

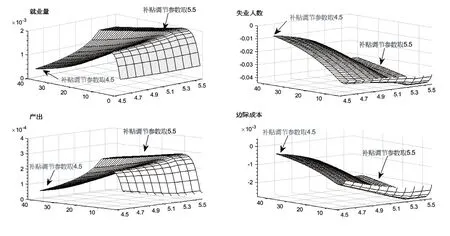
图1“助企纾困补贴+扩张性财政政策”组合的脉冲响应（ψ=4.5-5.5）

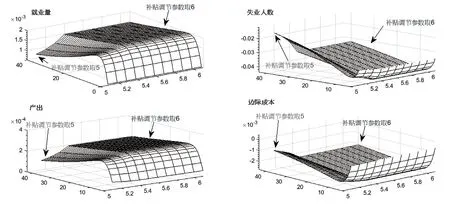
图2“助企纾困补贴+扩张性财政政策”组合的脉冲响应（ψ=5.3-6）

从图1 可以得出，为了应对疫情冲击等外部不利因素对经济的影响，在政府采取扩张性财政政策时，可以通过对企业发放助企纾困补贴以进一步增强扩张性财政政策对稳定经济和促进就业的作用效果。另外，从图1 中还可以看出，当政府提高发放助企纾困补贴的力度时，即ψ从取值4.5 上升至5.3，失业人数和中间品厂商的边际成本下降得更低，就业总量和产出上升得更高。这说明了在适度增加助企纾困补贴力度时，政府支出稳定经济、促进就业的效果也逐步上升。

从图2 可以看出，当助企纾困补贴力度达到一定限度时，即当ψ取值超过5.3 时，补贴政策对就业量、失业人数、产出和中间品厂商边际成本不再产生显著影响，图2 各宏观经济变量受到扩张性财政政策冲击时的脉冲响应曲面呈现水平状，未发生显著波动。这说明实施助企纾困补贴政策，并不是补贴得越多效果就肯定越好，而是要有一定的限度；超过限度以后，补贴对稳定经济和促进就业的作用效果就变得很微弱了。上述实证结果与张彩江和陈璐（2016）阐述的观点是一致的，他们利用珠三角上市创新型企业数据进行的研究表明，由于创新活动的正外部性特点，企业倾向于通过内源融资进行研发；在外源融资中，政府补助对研发投入有显著促进作用。当政府补贴在适当的区间内，会促进企业研发投入；而若补助过多，则会挤出企业用于研发的其他资金投入，并不能起到促进企业创新的作用。

（二）“助企纾困补贴+宽松货币政策”组合的实施效果

考察助企纾困补贴参数ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到宽松货币政策冲击时所产生的脉冲响应，具体结果见图3 和图4。图3 中X 轴代表参数ψ取值，Y 轴代表ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到宽松货币政策冲击时所产生的脉冲响应期数，Z 轴代表上述待考察宏观经济变量的偏离稳态程度。图5 显示的是助企纾困补贴政策分别与宽松货币政策和扩张性财政政策搭配时的组合实施效果比较。

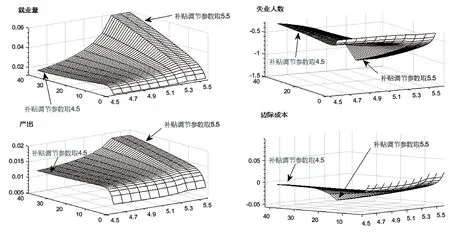
图3“助企纾困补贴+宽松货币政策”组合的脉冲响应（ψ=4.5-5.5）

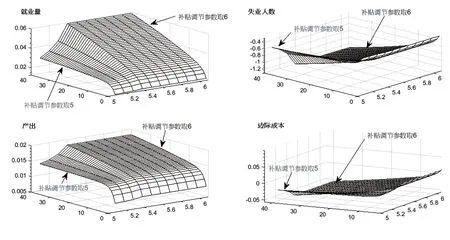
图4 “助企纾困补贴+宽松货币政策”组合的脉冲响应（ψ=5.3-6）

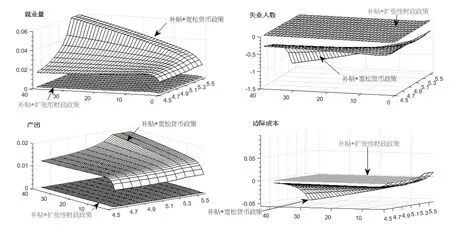
图5 助企纾困补贴政策与财政货币政策组合的实施效果比较

从图3 可以得出，在采取宽松货币政策时，可以通过对企业给予助企纾困补贴以进一步增强货币政策对稳定经济和促进就业的作用效果。提高发放助企纾困补贴的力度时，即参数ψ取值从4.5 上升至5.3 时，失业人数和中间品厂商的边际成本下降的更低，就业总量和产出上升的更高。这说明若适度提高助企纾困补贴力度，其增强宽松货币政策对稳定经济和促进就业的作用效果也会逐步上升。

从图4 可以看出，当助企纾困补贴力度达到一定限度，即当ψ取值超过5.3 时，补贴政策对就业量、失业人数、产出和中间品厂商边际成本不再产生显著影响，图4 中各宏观经济变量受到宽松货币政策冲击时的脉冲响应曲面呈现水平状，未发生显著波动。这说明助企纾困补贴政策与宽松货币政策搭配使用时，也不是补贴得越多效果就越好，而是有一定的限度。

图5 中深灰色的脉冲响应曲面代表“助企纾困补贴+宽松货币政策”组合下就业量、失业人数、产出以及边际成本对应的脉冲响应，而灰色脉冲响应曲面代表“助企纾困补贴+扩张性财政政策”组合下就业量、失业人数、产出以及边际成本对应的脉冲响应。之所以在两张曲面的合成图中，灰色脉冲响应曲面几乎表现为一张平面，原因是“助企纾困补贴+扩张性财政政策”组合下各变量对应的脉冲响应稳态偏离值相比较“助企纾困补贴+宽松货币政策”组合下各变量对应脉冲响应稳态偏离值过于微小。从图5 可以看出，“助企纾困补贴+宽松货币政策”组合对就业量和产出的正向作用显著大于“助企纾困补贴+扩张性财政政策”组合，但同时前者对失业人口和中间品厂商的负向作用也显著大于后者。总体上，与“助企纾困补贴+扩张性财政政策”组合相比，在“助企纾困补贴+宽松货币政策”协调配合情景下，经济基本面可以恢复得更为迅速。

（三）“助企纾困补贴+降低消费税”组合的实施效果

考察助企纾困补贴参数ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到降低消费税冲击时所产生的脉冲响应，具体结果见图6 和图7。图6 中X 轴代表参数ψ取值，Y 轴代表ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到降低消费税政策冲击时所产生的脉冲响应期数，Z 轴代表上述待考察宏观经济变量的偏离稳态程度。图7 中X 轴代表脉冲响应曲线的期数，图7 中的Y 轴ψ取不同值时就业总量、失业人数、产出以及中间品厂商边际成本受到降低消费税政策冲击时所产生的偏离稳态值。图8 显示的是助企纾困补贴政策分别与其他三种政策的组合实施效果比较。

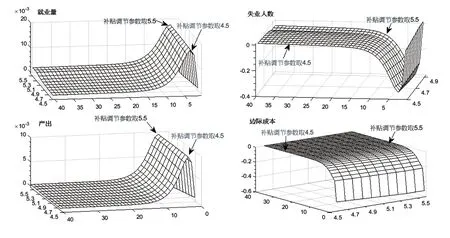
图6 “助企纾困补贴+降低消费税”组合的脉冲响应曲面（ψ=4.5-5.5）

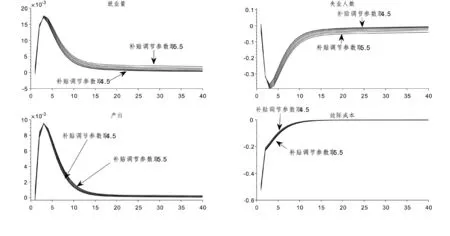
图7 “助企纾困补贴+降低消费税”组合的脉冲响应曲线（ψ=4.5-5.5）

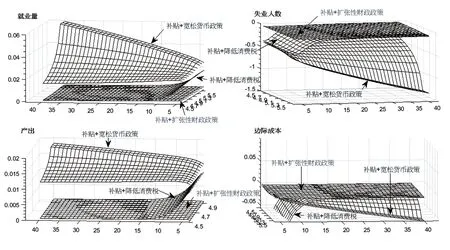
图8 助企纾困补贴政策与其他政策组合的实施效果比较

从图6 可以看出，在政府采取降低消费税的财政政策时，通过对企业发放助企纾困补贴可以进一步增强降低消费税对稳定经济和促进就业的作用效果。当政府提高发放助企纾困补贴的力度，即参数ψ从取值4.5 上升至5.5 时，失业人数和中间品厂商的边际成本下降的更低，就业总量和产出上升的更高。这说明如果适度增加助企纾困补贴的力度，降低消费税对稳定经济和促进就业的作用也会增强。由于图6 中各主要宏观经济变量的脉冲响应曲面从某些角度看变化幅度有些小，所以为更清楚地展示“助企纾困补贴+降低消费税”组合时各主要宏观经济变量的脉冲响应函数的变化趋势，在图7 中进一步给出了“助企纾困补贴+降低消费税”组合时各主要宏观经济变量的脉冲响应曲线，每一条脉冲响应曲线对应助企纾困补贴参数的一个取值，参数ψ从取值4.5 上升至5.5，图7 中每一个子图中的脉冲响应曲线个数为11 条。从这些主要宏观经济变量的脉冲响应曲线可以看出，在经济受到降低消费税的外生冲击后，不同补贴参数下就业量的脉冲响应曲线出现显著上升，而产出上升幅度相对较小，这说明降低消费税并且同时增加助企纾困补贴对促进就业的作用要显著大于稳定经济的作用。另外，当经济受到降低消费税的外生冲击后，不同补贴参数下失业人数的脉冲响应曲线出现显著下降，而边际成本下降的幅度相对较小，这说明“助企纾困补贴+降低消费税”组合对降低失业率的作用要显著大于降低企业边际成本的作用。

为进一步比较助企纾困补贴政策分别与其他三种政策的组合实施效果，在图8 中将三种政策对应的脉冲响应曲面合在一张图中进行直观比较。可以看出，“助企纾困补贴+宽松货币政策”在增加就业和促进经济恢复方面的表现显著优于“助企纾困补贴+降低消费税”和“助企纾困补贴+扩张性财政政策”，而在降低失业人数方面，“助企纾困补贴+宽松货币政策”也是三种政策组合中实施效果最好的。此外，“助企纾困补贴+降低消费税”在增加就业和促进经济恢复方面也显著优于“助企纾困补贴+扩张性财政政策”，但政策的组合实施效果比起“助企纾困补贴+宽松货币政策”要相对差一些。然而，在脉冲响应曲面对应的前10 期脉冲响应中，“助企纾困补贴+降低消费税”对降低企业边际成本效果是三种政策组合中最明显的，“助企纾困补贴+宽松货币政策”次之，“助企纾困补贴+扩张性财政政策”的效果是相对最弱的。但当脉冲响应的期数在11 至40 期之间，“助企纾困补贴+宽松货币政策”对降低企业边际成本的效果又变为三种政策的组合实施效果里最好的，这说明“助企纾困补贴+降低消费税”对降低企业边际成本的作用从短期来看是三种政策的组合实施效果里最好的，但是从长期来看，“助企纾困补贴+宽松货币政策”对降低企业边际成本的效果又变为三种政策组合中实施效果里最好的。总体上来看，与其他两个政策组合相比，“助企纾困补贴+宽松货币政策”对促进就业和提高产出的效果更为明显。

（四）不同政策组合对社会福利的影响

为进一步分析助企纾困补贴政策与其他政策组合对于社会福利水平的改进效果，采用Schmitt 和Uribe（2007）的社会福利测度方法对不同政策组合下的条件福利损失进行量化分析。条件福利损失效应可表示为理论模型中政策实施时（Policy Economy）相对于无政策实施时（Benchmark Economy）所需要补偿的消费比例λcond。具体来说，假设无政策实施时消费者的预期终生消费水平记为WH0,t（CH0,t，NH0,t），其中CH0,t和NH0,t分别表示无政策实施时消费者的消费水平和劳动供给；有政策实施时消费者的预期终生消费水平记为WH1,t（CH1,t，NH1,t），其中CH1,t和NH1,t分别表示有政策实施时消费者的消费水平和劳动供给，则根据家庭的效用函数的设置可得WC：

为了求出政策实施时相对于无政策实施时所需要补偿的消费比例λcond，令：

即可解出消费比例λcond：

表2 给出了助企纾困补贴参数ψ取不同值时，在不同政策情景下的条件社会福利损失。λcond的取值可正可负，也可以等于零。如果λcond的取值为负数，则代表政策实施情形下的社会福利水平比起无政策实施时更高，反之亦然；如果λcond的取值为零，则代表两种情形下的社会福利水平无差异。从表3 可以看出，当政府提高发放助企纾困补贴的力度，即参数ψ取值从4.5 上升至5.9 时，三种政策组合下的社会福利水平均比起无政策实施时有所改进，其中“助企纾困补贴+宽松货币政策”对于社会福利水平的改进效果是最好的，“助企纾困补贴+降低消费税”的改进效果次之，“助企纾困补贴+扩张性财政政策”的改进效果最差。另外，伴随参数ψ的增大，“助企纾困补贴+宽松货币政策”对于社会福利水平的改进效果先是小幅增加，达到最大值之后又小幅回落，说明在实施“助企纾困补贴+扩张性财政政策”时，并不是补贴得越多，社会福利水平改善就越大，而是有一定的最佳力度，超过最佳力度以后，其对社会福利水平反而会形成负面影响。

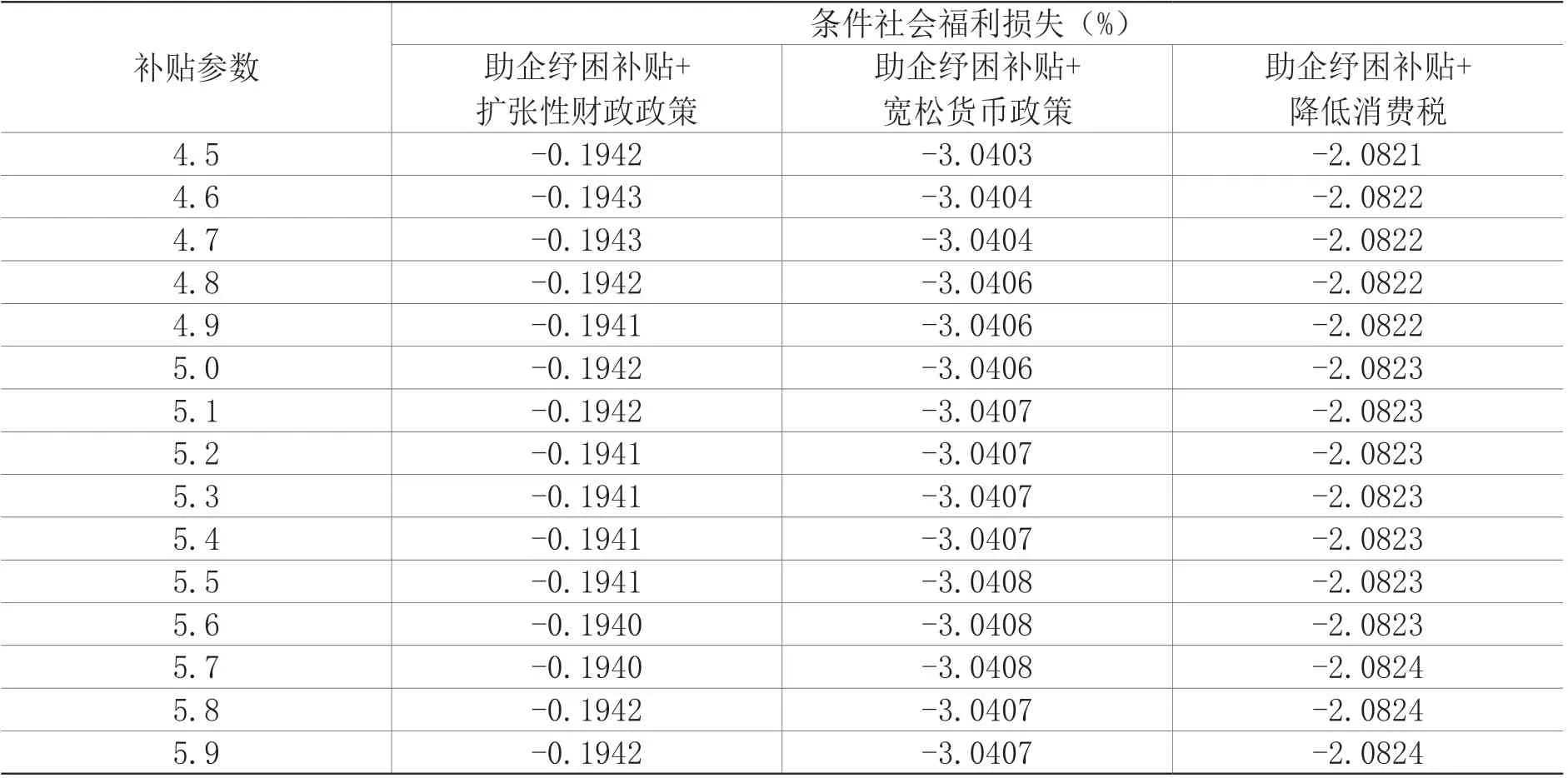
表2 不同政策情景下的条件社会福利损失比较

综上所述，在三种不同政策组合中，“助企纾困补贴+宽松货币政策”在增加就业、提高产出、增加社会福利方面都是效果最好的，“助企纾困补贴+降低消费税”次之，而“助企纾困补贴+扩张性财政政策”的效果最差。可能的原因为：“助企纾困补贴+宽松货币政策”的作用机制不只是通过利率下行减少投资成本，还包括改变市场流动性和风险溢价，强化企业、居民和政府的资产负债表等，并且通过提高消费者对借贷的意愿，鼓励消费者进行消费，从而刺激经济增长。借助宏观经济学中的IS-LM 模型，可以更直观地进行解释。在图9 中，扩张性财政政策实施后，总需求上升，进一步导致产出Y 上升，IS 向右平移，如果利率R 保持不变，均衡产出水平将变为Y2，但因为产出的上升在货币市场中会导致利率R 上升，利率的上升会导致消费和投资的下降，总需求就会减少，产出会下降一部分，均衡产出水平变为Y3，从Y2到Y3这部分的产出被“挤出”。正是由于挤出效应的存在，在一定程度上削弱了扩张性财政政策在拉动经济增长和促进就业方面的作用，使得“助企纾困补贴+宽松货币政策”在增加就业和促进经济恢复方面要显著优于其他两个政策组合。至于实证检验发现疫情冲击下财政货币政策的助企纾困效应明显（马征程和潘佳佳，2023），这些文献的研究结果与本文模拟分析结果并不存在矛盾，原因是以往文献只验证了疫情冲击下财政货币政策助企纾困的有效性，并没有将财政政策与货币政策的有效性进行比较。事实上，本文的理论模拟分析结果也表明“助企纾困补贴+扩张性财政政策”能够产生增加就业和促进经济恢复的效应，只是与“助企纾困补贴+宽松货币政策”相比较而言效果差一些。

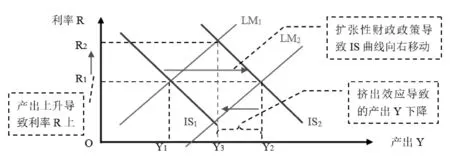
图9 IS-LM 模型中的挤出效应分析

（五）稳健性检验

为进一步验证三种政策组合的实施效果，首先对补贴参数ψ单独赋值，分别取值为4.5和5.3。然后从剩下的13 个贝叶斯估计参数的联合后验分布中进行随机抽样，一共进行19000 次采样。最后将上述抽样所得的13 个参数的19000 个贝叶斯估计样本结合7 个校准的参数和一个单独赋值的补贴参数共计21 个参数，分别计算三种政策组合的40 期后验脉冲响应函数，后验脉冲响应函数曲线如图10 和图11 所示。图中实线代表每一期后验脉冲响应函数的均值，实线两侧的虚线表示90%置信区间。

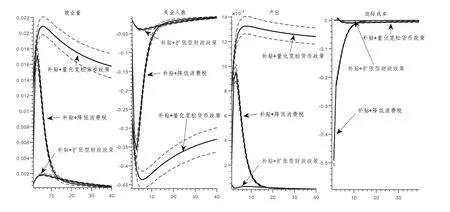
图10 ψ=4.5 时的贝叶斯后验脉冲响应曲线

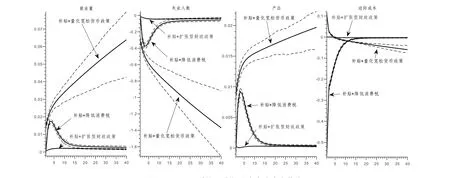
图11 ψ=5.3 时的贝叶斯后验脉冲响应曲线

从贝叶斯后验脉冲响应曲线同样可以看出，“助企纾困补贴+宽松货币政策”在增加就业、促进经济恢复、降低失业人数三方面都要优于“助企纾困补贴+降低消费税”和“助企纾困补贴+扩张性财政政策”。同时还可以看出，在增加就业和促进经济恢复方面，“助企纾困补贴+降低消费税”要优于“助企纾困补贴+扩张性财政政策”。在降低企业边际成本方面，三种政策组合的贝叶斯后验脉冲响应曲线所得出的结论与前文结论一致，不再赘述。

六、结论与政策启示

自新冠疫情发生以来，我国各级政府相继出台了多项助企纾困补贴政策来帮助企业渡过难关、稳定生产经营。本文构建包含招聘摩擦和工资黏性的DSGE 模型，探究助企纾困政策与三种常规政策组合对增加就业和促进经济恢复的效果及作用机制，结果表明：第一，“助企纾困补贴+宽松货币政策”无论是在增加就业、提高产出还是对于社会福利水平的改进方面都是三种政策组合中效果最好的，“助企纾困补贴+降低消费税”效果次之，而“助企纾困补贴+扩张性财政政策”的效果相对来看是最弱的。第二，助企纾困补贴政策并不是补贴力度越大政策效果就越好，超过一定的补贴限度以后，其对经济和就业的促进作用就变得非常微弱，甚至可能对社会福利产生负向影响。第三，在降低企业边际成本方面，“助企纾困补贴+降低消费税”从短期来看是三种政策组合中效果最好的，但是从长期来看“助企纾困补贴+宽松货币政策”的效果最好。

以上结论带来的政策启示：第一，鉴于“助企纾困补贴+宽松货币政策”在增加就业和促进经济恢复方面要显著优于其他两个政策组合，建议政府宏观调控部门在采取助企纾困补贴政策的同时实施相对宽松的货币政策，最大限度地发挥助企纾困补贴政策的积极效应。第二，在实施助企纾困补贴政策时，不能搞“大水漫灌”，避免出现过犹不及的情况，为此要掌握好补贴政策的力度，确保财政资金用在“刀刃”上。第三，鉴于“助企纾困补贴+扩张性财政政策”在增加就业、促进经济恢复、提高社会福利等方面的效果不甚理想，有必要精准找到积极财政政策的着力点，提高财政政策传导效率，更加注重加强与货币政策、就业政策的协调配合，更好地发挥财政政策稳就业、促复苏的作用。要统筹用好就业补助、创业补贴、创业担保基金、政府引导基金等财政及政策性资金，落实落细就业创业保障政策，为企业增收、降本、稳岗提供更加有效的支持。